2元1次方程式 解き方
2元1次方程式は1つでは解が無数にあったが,連立方程式になると (特殊な場合を除いて)解は1組である。 この連立方程式の解を求めることを 「連立方程式を解く」 という。 連立方程式を解く 連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に 加減法 と 代入法 がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」.

2元1次方程式 解き方. 一次方程式とは、ざっくりと説明するとこんな感じです。 だけど ん?一次ってなんだ?? ってなっちゃうよね。 ということで、一次方程式とは?ということを簡単に理解できるよう解説していきます。 この記事を通し. 連立方程式の解き方 連立方程式は,2種類の文字のうちの一方を消去して,他方の文字についての1元1次方程式をつくることによって解く。 加減法 :どちらかの文字の係数の絶対値をそろえ,2つの式の左辺同士,右辺同士を加減することによってその文字を. 2階線形微分方程式の解き方(まとめ) この記事では、 二階線形微分方程式 の解き方について解説します。 この微分方程式は、大きく分けて答えが3パターンあるため、 3種類の解き方 についてそれぞれ 例題付き で解説しています。 目次 2階線形微分.
2 2次方程式 を解く① 平方根 利用型 例えば、を満たすxを考えよう。 は「xを二乗すると4になる」という意味。 二乗して4になる数は「 」。 これが方程式の解。 例えば、を満たすxを考えよう。 二乗して5になるのは、「 」これが方程式の解。 の形にできれば、、 平方根 の知識を使って方程式を解ける。 例題02 以下の 2次方程式 を解け (1) (2) (3) (4) (5) 解説 まず、 の形に変形しよう. 中学2年の数学で習う連立方程式の解き方代入法の解説と問題演習 問21 次の連立方程式を解きなさい。 元の問題が小数や分数の係数のときは,次の例のように両辺を10倍,100倍,して整数に変えて使ってください.. これで方程式の解き方の第一ステップは終了! 解き方2 「数字」を右によせろ! ! 次はx以外の項。 つまり、数字の項を右側によせちゃおう! ! さっきの例でいえば、「2」と「10」が数字の項だね。 右への寄せ方は手順1と同じだよ。 そう。 移項というワザを使ってやるんだ。 符号を変えながら数字の「2」という項を右へ移してやるとこうなる! これで解き方のステップ2も終.
2次合同式 x^2 ≡ 5 (mod 11) の解き方をご教授願います。 解はx ≡ 4, 7 (mod 11)です。 私は、式の両辺にー4してx^2-4≡1 (mod 11)としてから、 11k+1=x^2-4にして、k=0~13まで調べて 、解を求めました。 しかし、 このやり方だとkが負の整数の時、kが14以降に. ところで、1次方程式の解は1つでしたが、2次方程式では解が基本「2つ」になります。 2つになることで、1次方程式のような簡単な移項だけでは解くことが出来ません。 このやり方については、別の記事で詳しく解説していきますね! まとめ いかがでしたか?. 出題領域 数と式。この問題を完璧に解くために,せめて以下の知識・技能が必要です。 (1)1の立方根 (2)3乗式の因数分解 (3)二次方程式の解き方 (4)因数分解の仕方 では,問題を解いてから解答を見ましょう。 解答 仮定より,式①は となる。.
a 1 xb 1 y=c と a 2 xb 2 y=d の連立方程式を考えてみます。 a 1a 2 =b 1b 2 であれば、二つの直線の傾きは等しくなるため、「重なる (不定解)or平行(不能解)」のどちらかであることが分かります。 さらに、定数項のcとdの比に注目して. ここで行列の方程式の\(x\)は\(x_1\)と\(x_2\)の列ベクトルを表しています。 ではこの手順に従って連立方程式を解いてみましょう! まずは連立方程式を行列の形に変形します。 \ $$\left\left = \left$$ 次は逆行列を求めていくよ 逆行列の求め方は覚えていますか?. 方程式の変数が1文字しか出てこないので偏微分ではなく常微分で表します。要するに高校等でやってきたいわゆる「普通の微分」に書き換えます。 $$\frac{\partial^2}{\partial x^2}→\frac{d^2}{dx^2}$$ このような書き換えをすると方程式全体は次のようになりますよね。.
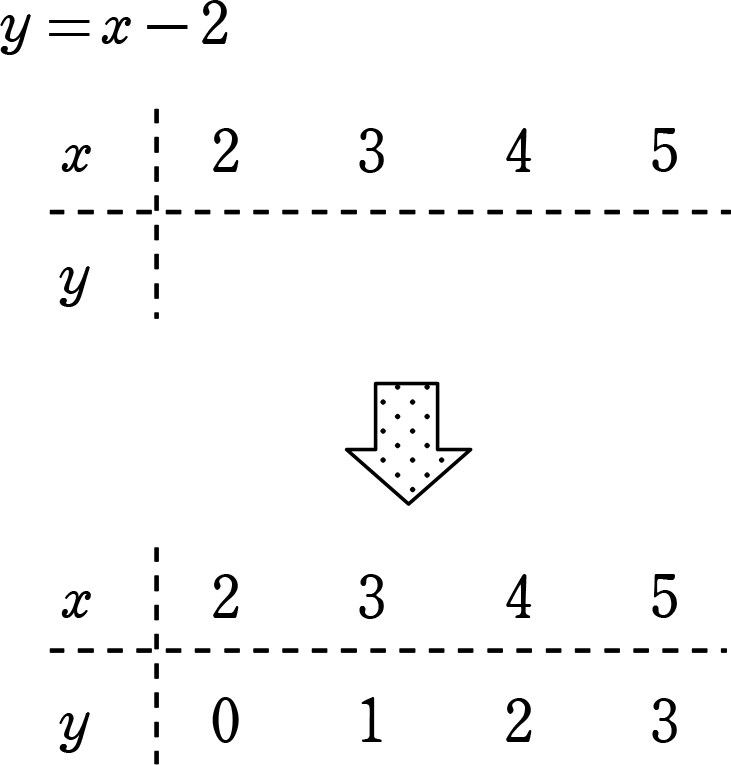
二元一次方程式 = 1次関数 でOKです! ! このように、二元一次方程式では xの値 (解)が無数にあるように、 それに対する y の値 (解)も無数にあるということになります。 でありますので、二元一次方程式の問題では、必ず xに、「 条件づけ 」や「 範囲指定 」があります。 《 例 》 xy = 2 において、xが2から5までの整数のとき、yの値を求めましょう。 → xは2~5の整数という範囲指定ですね x. それでは,2 元1 次方程式の解と連立方程式の解について学習しましょう。 2 元1 次方程式2 x-3y=6 を成り立たせる ,yの値の組(x,y)を①~③の中からすべて 選びなさい。. 1次方程式の解き方はルールを覚えれば簡単 今回扱うのは「 1次方程式 」です。 みなさんは新しく「方程式」という内容を学習していきますが、この方程式は数学において非常に非常に役に立つものですから、ぜひ身につけていきましょうね! 閉じる.
2次方程式の解き方の1つに、因数分解を行う方法があります。例えば、下記の2次方程式を因数分解すれば(x1) 2 です。よって解はx=-1です。 因数分解は公式を暗記すると計算が早くなりますが、因数分解の計算方法(たすき掛けなど)を理解しましょう。. 二元一次方程式の解を求めるには、 2つ以上の二元一次方程式が必要だよ。 たとえば、 2x5y =26 3x2y= っていう2つの方程式があったら、 さっきの2つの解のうち、 (x, y) = (18, 2) (x, y) = (8, 2) しか成り立たなくなるよ。 ってことで、 二元一次方程式の解を1つに決めたかったら、 2つの二元一次方程式を用意する ってことをおぼえておこう。 このように、2つの方程式を組にし. 2元連立方程式の解を求めます。 2次関数の計算 ご意見・ご感想 使いやすすぎます。1分かからないうちに使い方が分かりました。.
三次方程式の解き方 三次方程式を解くためには、基本的に因数分解が必要となります。 この因数分解のやり方には、次の \(2\) 通りの方法があります。 因数分解の公式 を利用する;. 連立方程式の解き方 この頁では,未知数の個数と方程式の個数とが等しい (*)ような連立1次方程式の解き方を扱う.さらに,係数行列に逆行列が存在する場合 (**)だけを扱う. 連立1次方程式の解き方 未知数がn個 x 1, x 2, x 3, ··, x n ,方程式がn個の連立1. 目次 1 1次不定方程式の単元で学習すること 2 1次不定方程式について 3 1次不定方程式の解き方と解の表し方 31 1次不定方程式の解き方 32 1次不定方程式の一般解を求めてみよう 4 1次不定方程式を扱った問題を解いてみよう 41 問(1)の解答・解説;.
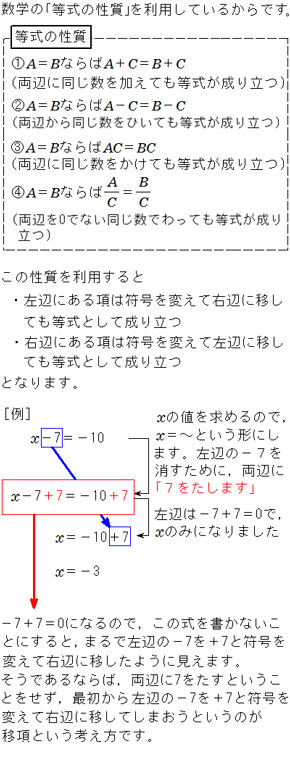
次の連立1次方程式を行基本変形によって解く 1行目と2行目を交換する← (1, 1)成分を1にするため 2行目から1行目の2倍を引く,3行目から1行目の4倍を引く,4行目から1行目の3倍を引く 2行目を−5で割る,3行目を3で割る 1行目から2行目の4倍を引く,3行目から2行目の−5倍を引く,4行目から2行目の−5倍を引く 3行目と4行を入れ替える,さらに3行目を−1倍する 1行目から3行目の6倍を引く,2. 普通の2元1次方程式(x、y)の場合、 x+2y=3 x=1 の二つの式からx、yを求めよ、という問題はわかりますよね。それと同じことです。 これは4元一次方程式ですが、多元1次方程式の解き方はわかっていますか?. 方程式を解く ( xを求める) ためには、「 等式の性質 」を利用します。 例えば、赤のペットボトル (1本500 g) を2本と、 青のペットボトル (同500 g) を2本、 天秤にのせます。 つり合っていますね。 これを文字で表すと「公式」になります 等式の性質 A=B ならば、 となりますが、 実際、方程式を解くときは、① (両辺に+)と② (両辺に-)は「 移項 」 (後述)でカバーしますので、 結局、使うもの.
今回は、補足として2元2次連立方程式の解き方を見ていこう。 基本的な考えは、連立方程式と同じで、文字を減らすことを考えればよい。 前回 ←2次方程式の解き方(3)(難) 次回 →解の問題(1)(代入、解から式を作る、直前の形)(基~標). 2つの未知数 x, y のどちらかの 係数が等しいとき は、左辺どうし、右辺どうしをそれぞれ 引く と1文字を消去できます。 この問題では y の係数がそろっているので、 y が消去できて x だけの方程式になります。 →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。. つまり1元。 それが2元(文字\(\,2\,\)つ)まで使えるというだけで、分からないもの、求めたいものを\(\,2\,\)つの文字を使って表すことができる便利なものが増えただけです。 次方程式になりますが、解き方は同じなのでこの単元で解き方を身につけて.
こんにちは、ももやまです。 今回は、前回に引き続き連立微分方程式について説明していきたいと思います。 今回は、4つの連立微分方程式の解き方 高階(2階以上)微分方程式に変換する方法 行列の対角化・指数. この解の公式には、分母に2が入っていません。そうなるように、元の2次方程式の係数を、以下の様に定めたからです。 aX 2 +2bX+c=0 解の公式は、前提条件の2次方程式を変えれば、この様に形が変わって来ます。. 1次2次連立形の連立方程式は,1次式の方を1文字について解き,2次の方に代入すると解けます. (解答) 1次2次連立形の連立方程式の解は,直線と楕円,放物線,双曲線などの2次曲線との共有点を表し,一般には2組あります (1)より y=2x1 (1’) (1’)を (2)に代入する x 2 (2x1) 2 =1 5x 2 4x=0 x (5x4)=0 x=0 のとき, (1’)に戻すと, y=1 のとき, (1’)に戻すと, (答) 2次2次連立形.
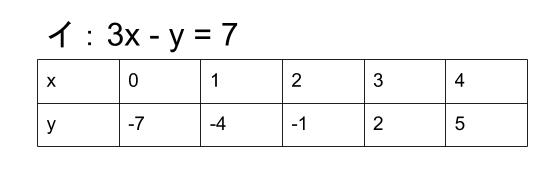
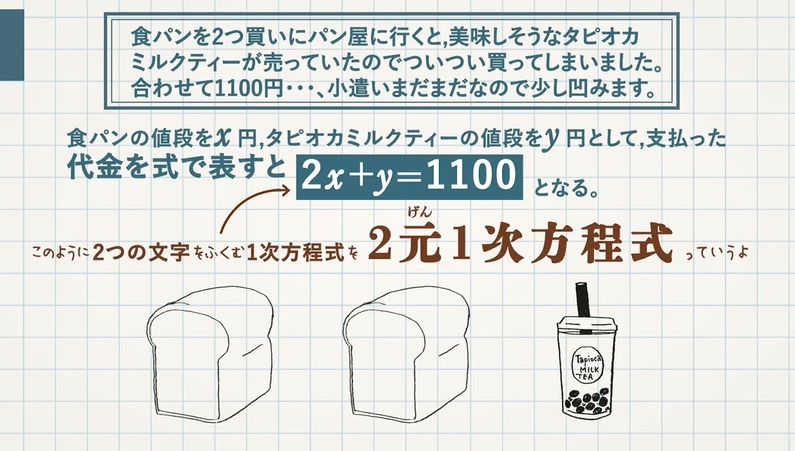
中学2年の数学で習う連立方程式の解き方加減法の解説と問題演習 問21 次の連立方程式を解きなさい。 元の問題が小数や分数の係数のときは,次の例のように両辺を10倍,100倍,して整数に変えて使ってください.. 解き方は、左辺は二乗を取り、右辺は平方根にする、ですね。 実際に見てみましょう。 x²=5 x=±√5 平方根の単元で学習した通り、平方根にする時は±である事に注意しましょう。 やはり、解の公式を用いた計算よりも、計算は、ずっと楽です。 最後はやっぱり練習! 以上で、二次方程式の解き方は全てとなります。 他の計算問題同様、解き方を理解した上で、実際に色々な問題を解き慣れていかな. 2元1次方程式とは x2y = 9 x 2 y = 9 このように、 2 2 種類の文字の項がある 1 1 次式を、方程式と見た場合 2 2 元 1 1 次方程式といいます。 ※関数とみれば 1 1 次関数(次の章で学びます)です。 あまり言葉にこだわる必要はありません。 等式の変形をする.
2元1次方程式と呼ばれる「 2つの変数 (文字) 」と「 最大次数が1 」の式で表されます。 連立方程式の解き方は大きく2つあります。 それは、 加減法 代入法 です。 どちらを用いても解ける問題が大半ですが、それぞれの特徴を抑えつつ、簡単に解説していきます。 加減法を用いた連立方程式の解き方 加減法 とは、どちらかの文字の係数の絶対値をそろえ、左辺どうし、右辺どうしを加えたり引いたり. 掃き出し法による3元1次連立方程式の解き方の手順 準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめる. Ⅰ.1元1次方程式 1元1次方程式 ax+b=0(a,b は定数)の形で表わされる等式の 解き方 ① 文字の項を左辺に、数字を右辺に移項する。 ② 両辺を整理して、ax=bの形にする。 ③ 両辺をaで割る。 例 移項 a x= b の 形に整理.
4元1次方程式 { a 11 x 1 a 12 x 2 a 13 x 3 a 14 x 4 = b 1 a 21 x 1 a 22 x 2 a 23 x 3 a 24 x 4 = b 2 a 31 x 1 a 32 x 2 a 33 x 3 a 34 x 4 = b 3 a 41 x 1 a 42 x 2 a 43 x 3 a 44 x 4 = b 4.

第1章 連立方程式
1
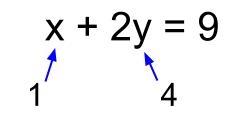
中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su
2元1次方程式 解き方 のギャラリー

2元1次方程式のグラフ 中学生 数学のノート Clearnote

連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri

二元一次方程式の文章題のやり方とこの写真の問題と Clearnote

高校数学 3元連立1次方程式 一般型と循環型 受験の月

Iseqi Pukiwiki

2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する

99以上1 次方程式文章題 シモネタ

連立方程式とその解 まなびの学園
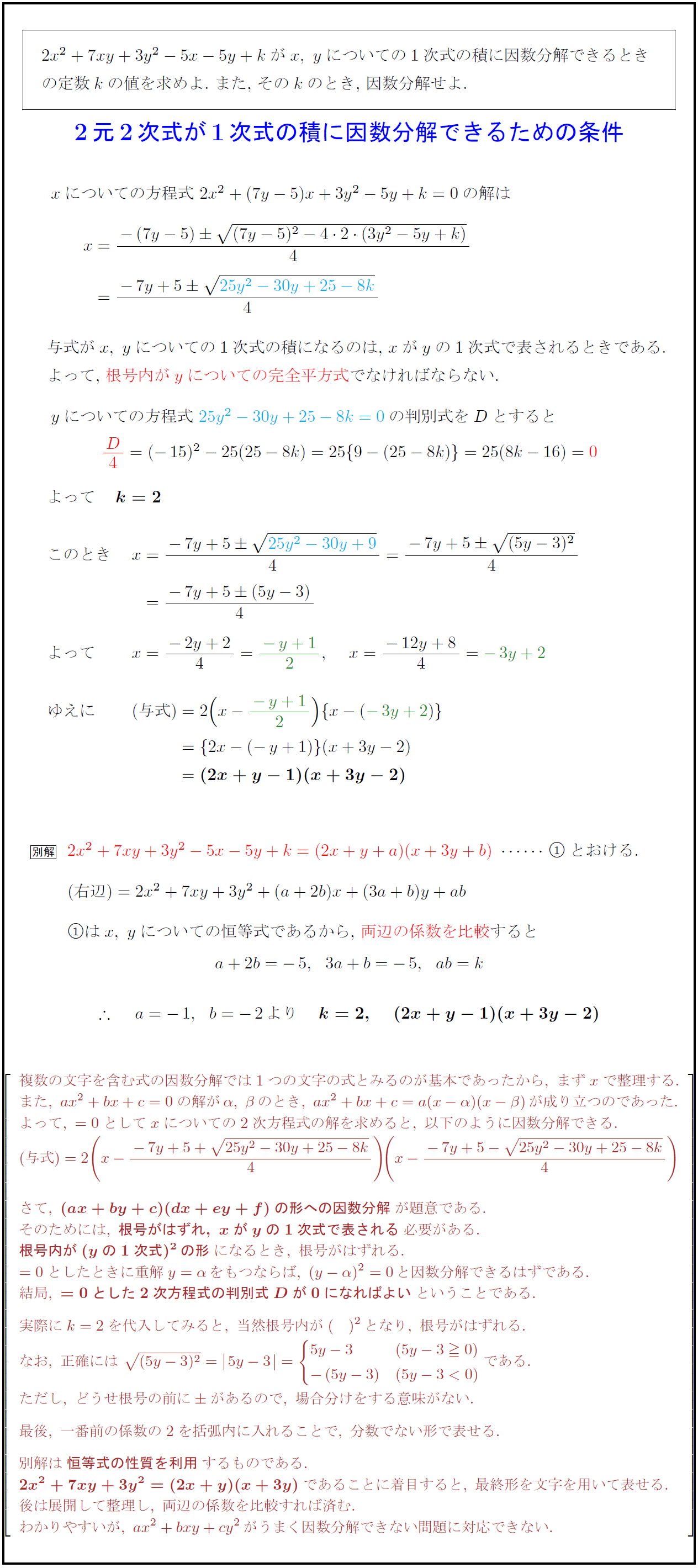
高校数学 2元2次式が1次式の積に因数分解できるための条件 受験の月
中学数学 連立方程式 二元一次

不定方程式ax by c c 0 の整数解の求め方 数学 苦手解決q A 進研ゼミ高校講座

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点
なぜ2元1次方程式の解は無限にあるのですか バカでも分かるよう Yahoo 知恵袋

Zoom二元一次看錯係數 Youtube
中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su
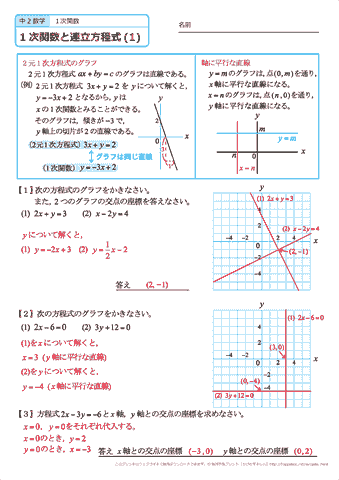
中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
第1章 連立方程式

高校数学 文字係数の2元連立1次方程式 受験の月

中2 二元一次方程式 解の求め方 日本語版 Youtube
二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ
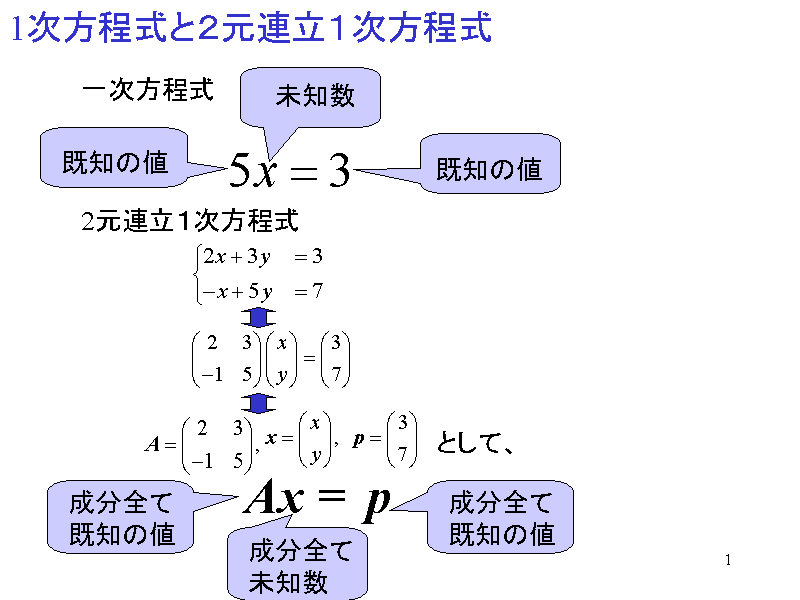
1次方程式と2元連立1次方程式

一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく

中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

第1章 連立方程式

数学 中2 35 二元一次方程式のグラフを書く Youtube

二元一次方程式的解 Youtube

2元1次方程式 Of Tomorrow Land

3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ

連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ
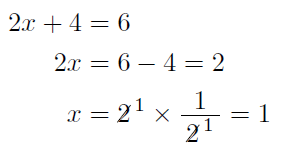
2元1次方程式 まなびの学園

食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張

整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張

中2数学 一次関数と方程式 二元一次方程式グラフの書き方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月

二次方程式の解き方 因数分解

三元連立方程式 1 中2数学 Youtube

数学の力を付けるヒントがある 齊藤数学教室 算数オリンピックから大学数学入門
連立 方程式 例題

連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
中学数学 連立方程式 二元一次

Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
連立方程式とは 連立方程式とその解 教遊者

二元一次方程解法
1
なぜ移項するとき符号がかわるのか 1次方程式 中学生からの勉強質問 数学 進研ゼミ中学講座

2元1次不定方程式 2 x 29y 1 の整数解を一組求めよ Clearnote
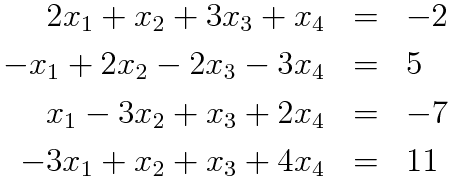
コンピュータ機械工学

連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく

18年6月のブログ記事一覧 2ページ目 身勝手な主張

1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト

連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張

二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題

この問題の解き方を教えてください お願いします Clearnote

中学数学 一次方程式

連立方程式の2つの解き方 代入法 加減法 数学fun

整数16 一次不定方程式が5秒で解けるとか無理じゃね 怜悧玲瓏 高校数学を天空から俯瞰する

食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張
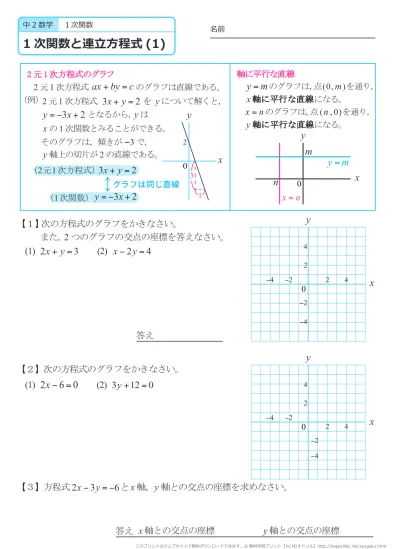
中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 このページの問題プリント 全部
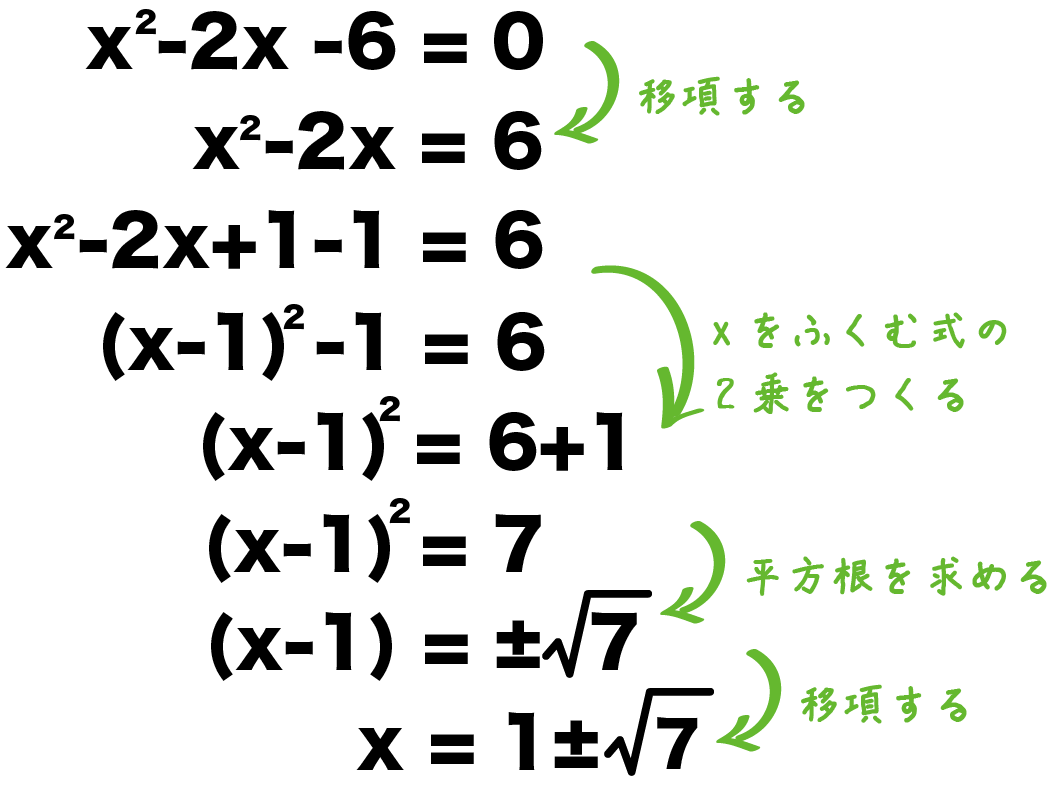
中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

二元一次方程式にする前の掛け算はなぜこのようなかけ方法を行ってるのですか Clearnote

ダウンロード2元1次方程式解 ニスヌーピー壁紙

最も共有された 1 次方程式分数 シモネタ
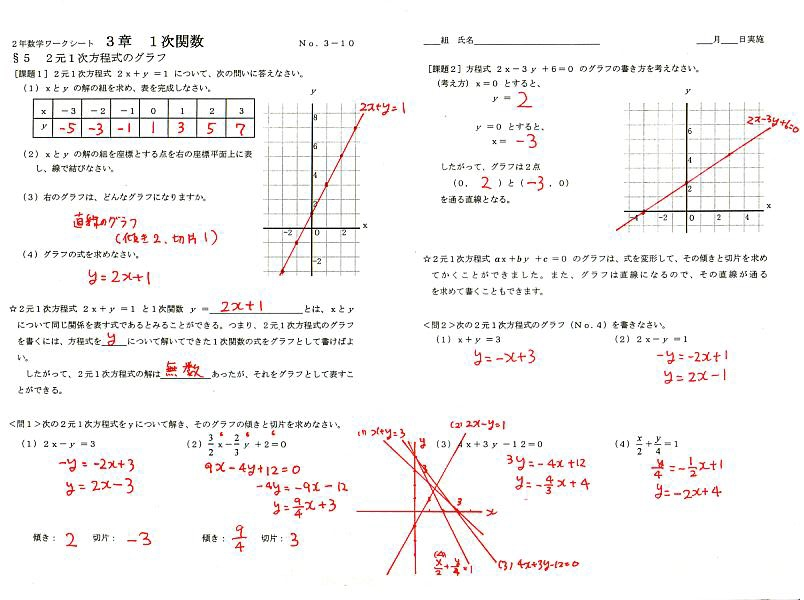
5 2元1次方程式のグラフ Mathweather4067のblog
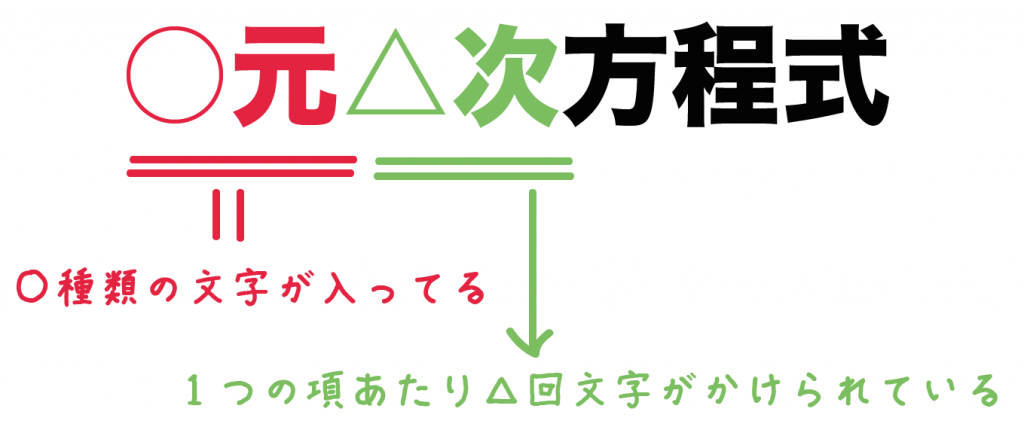
連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
中2数学 三元一次方程式についてです 5 番の問題がわかりません 解き Yahoo 知恵袋

中2数学 連立方程式 1 1 2元1次方程式 Youtube

連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学

高校数学で学習する連立方程式の解き方まとめ 数スタ
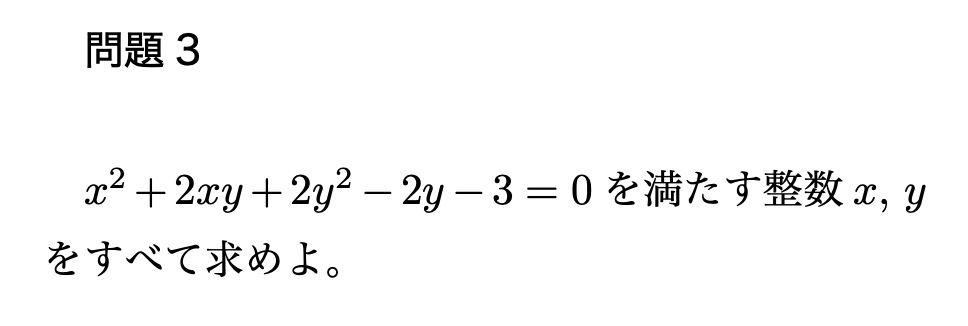
不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室

1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張

高校数学 2次方程式の実数解の個数 判別式 受験の月
Numpyで2元1次方程式の解を求める 偏った言語信者の垂れ流し

3分で分かる 二次方程式の問題の解き方をわかりやすく 合格サプリ

一次不定方程式 当てはまる整数解 特殊解 の求め方 すうがくブログ 式変形ch

用公式解解一元二次方程式 Youtube

99以上1 次方程式文章題 シモネタ

連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
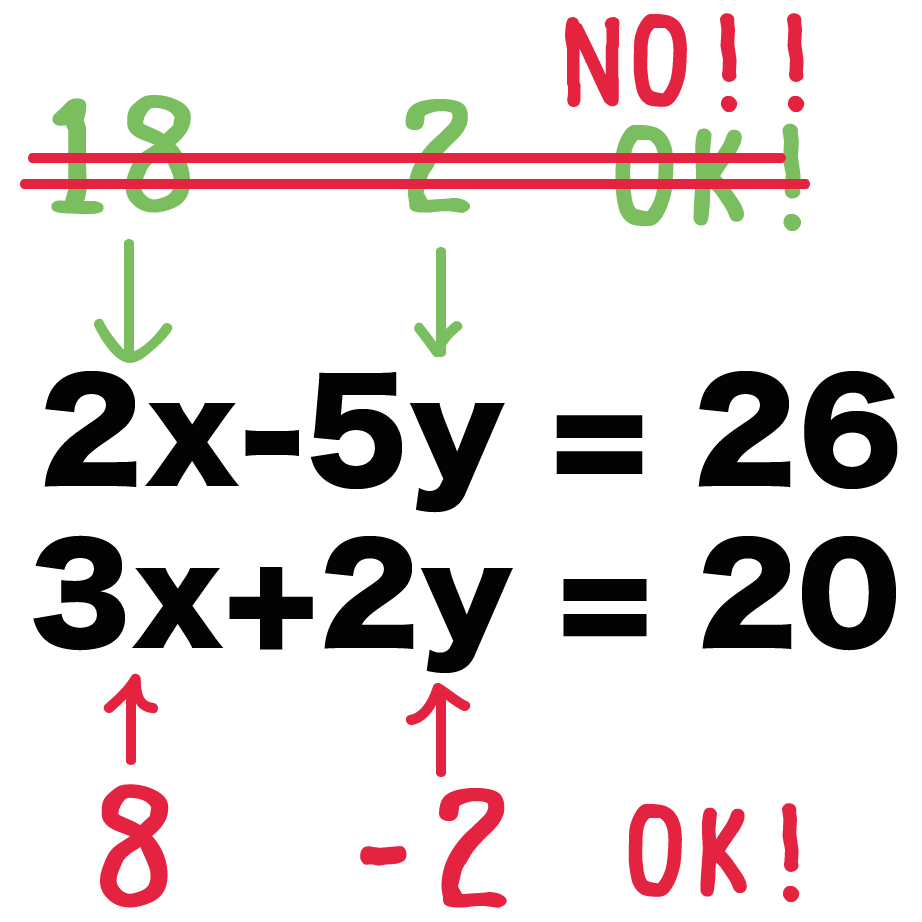
連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく

2元1次方程式 無料で使える中学学習プリント

連立3元一次方程式でこのように詰んでしまいます Clearnote

第1章 連立方程式

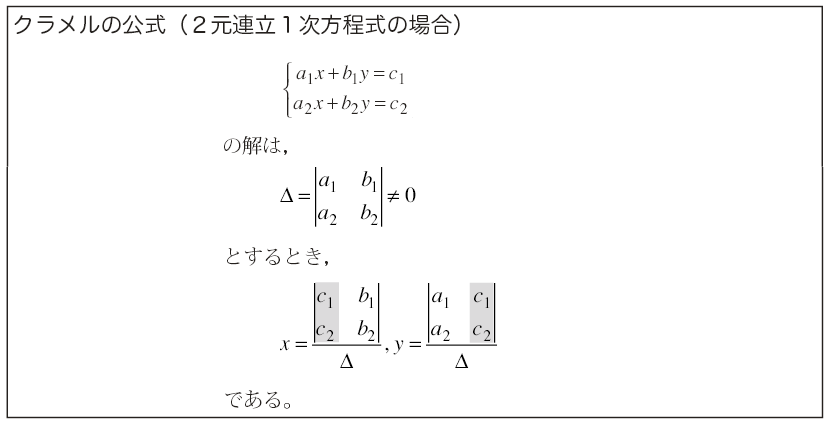
行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download

中学数学 中学2年 Vol 017 連立方程式の解き方 連立方程式とその解 二元一次方程式 Youtube
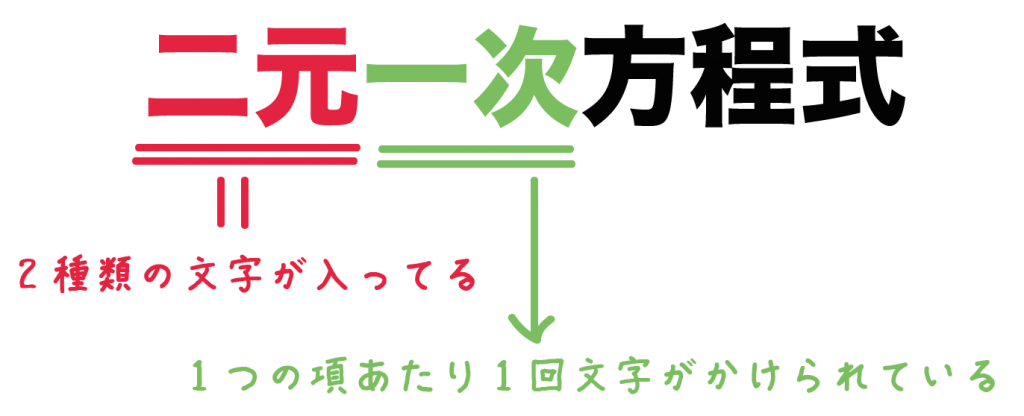
連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく

連立 方程式 例題

例題 連立3元1次方程式の解き方 勉強 Youtube スタディチューブ

連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく

2元1次連立方程式から2次の行列式へ
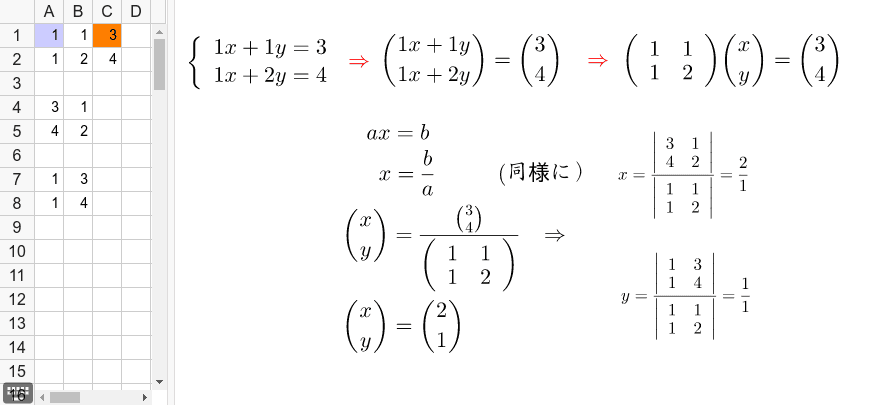
二元一次連立方程式 Geogebra

高校数学 2元2次連立方程式3パターン 受験の月
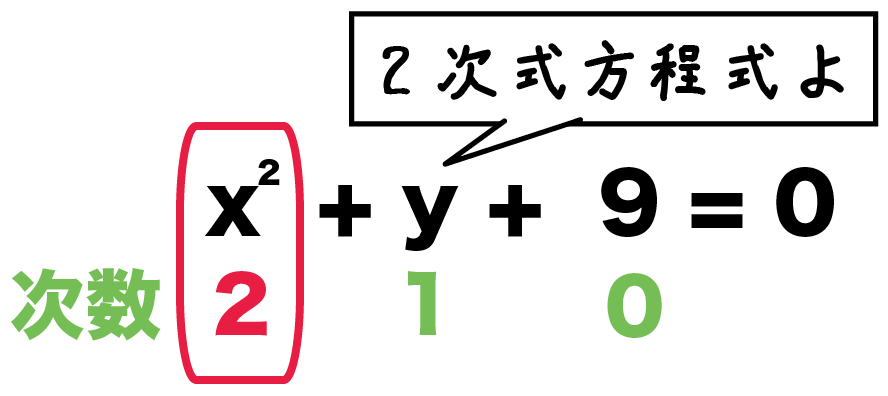
3分でわかる 二次方程式とはなんだろう Qikeru 学びを楽しくわかりやすく
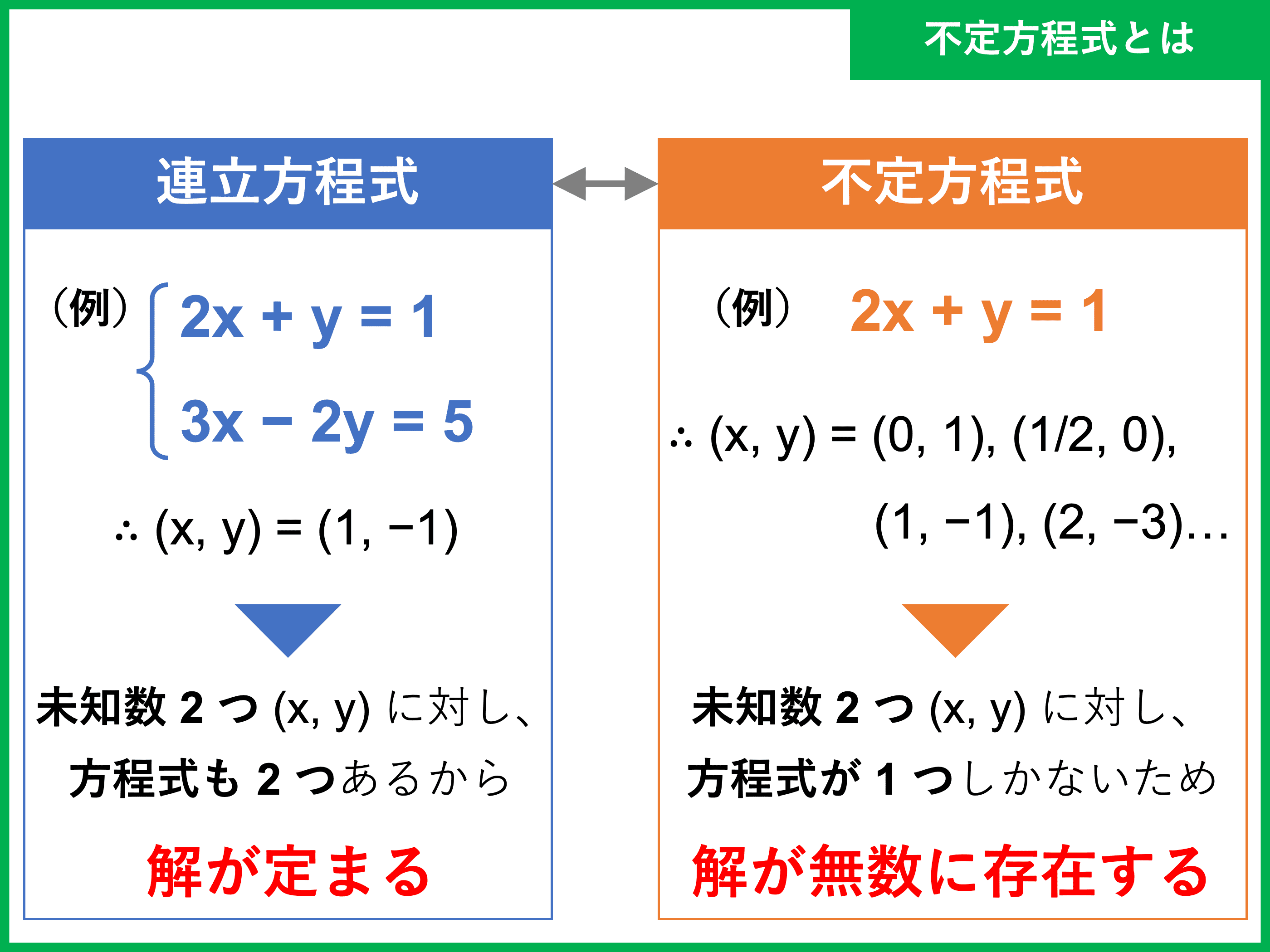
不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典
1

すど Ysmemoirs 学生講師の頃を含めるともう年くらい中学生に教えているけど まさかここに来て 2 元 1 次方程式の新しい解法に出会えるとは思わなかった 本日の授業でいろいろあった結果爆誕したやつ 数学授業の教材 Nitter
1

この三元一次方程式の解き方を教えて下さい Clearnote

連立3元1次方程式 身勝手な主張

中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム

連立3元1次方程式 まなびの学園

中2数学 二元一次方程式 証明 中学生 数学のノート Clearnote

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点




