2 次 関数 変化 の 割合
関数 y =-4 x 2 において、 x の値が n から n +2まで変化するときの変化の割合が24である。 このとき、 n の値を求めなさい。 <前: L25 変域とグラフ の問題 L26 変化の割合 の解答 :次>.

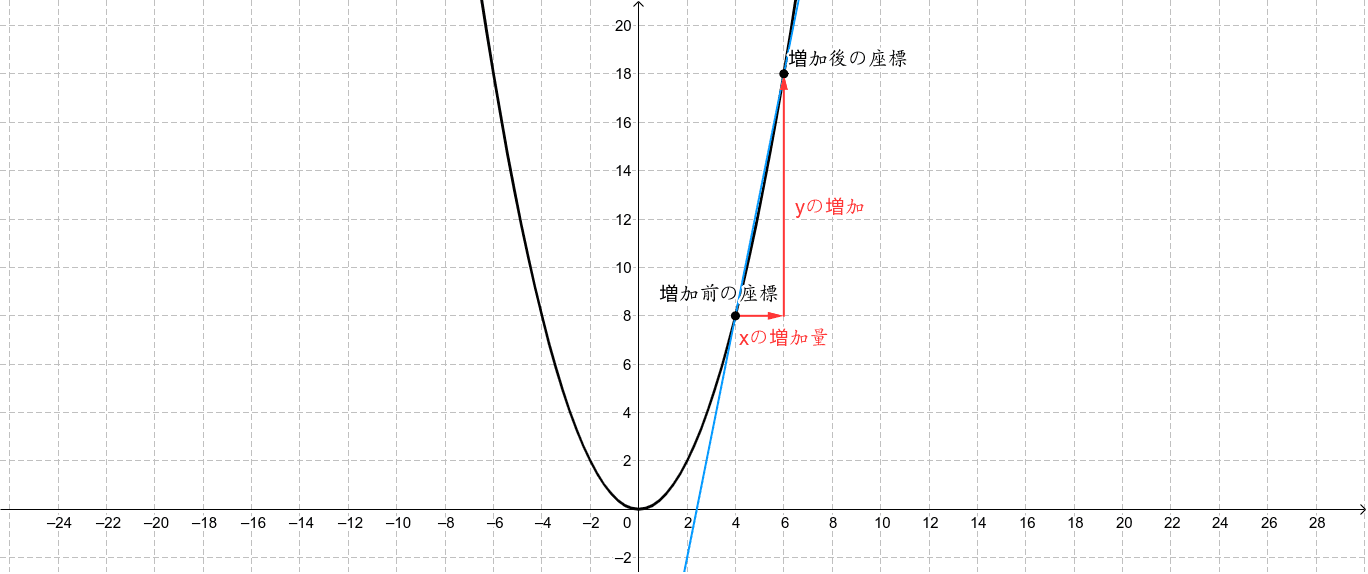
2 次 関数 変化 の 割合. ※以上のような訳で,1次関数(直線)の変化の割合は, x の係数を見たら即答え ですが,この裏技は直線の場合しか使えないので,反比例のグラフや3年生で習う2次関数のグラフでも真似してしまうと間違います. だから,どんな問題でも対応できるようにするには,地道に. 今回は、「y=ax 2 のグラフの変化の割合」について考えるよ。 中学2年生の「1次関数」の学習でも出てきた「 変化の割合 」って言葉、覚えているかな?. 変化の割合= yの増加量 xの増加量 変 化 の 割 合 = y の 増 加 量 x の 増 加 量 なので、この式に代入します。 変化の割合= ax2 2 −ax2 1 x2 −x1 変 化 の 割 合 = a x 2 2 − a x 1 2 x 2 − x 1 分子を a a でくくると 変化の割合= a(x2 2 −x2 1) x2 −x1 変 化 の 割 合.
1 1 次関数のときにもでてきた変化の割合です。 定義を覚えていますか? です。 でした。 変化の割合は常に一定であり、ただの「 a a 」 や「傾き」の別名でしかなかったものです。 2 2 乗に比例の y = ax2 y = a x 2 においては、変化の割合は一定ではあり. 変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ 4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download 変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ. <前:L18 連立方程式-割合編 の問題 L19 一次関数の値とその変化の割合 の解答:次> 練習問題1 以下の場合、時間を x ,水の量を y として、 y を x の式で表しなさい。 1 水の入っていない水槽に、毎分3m 2 の割合で水を入れる場合。.
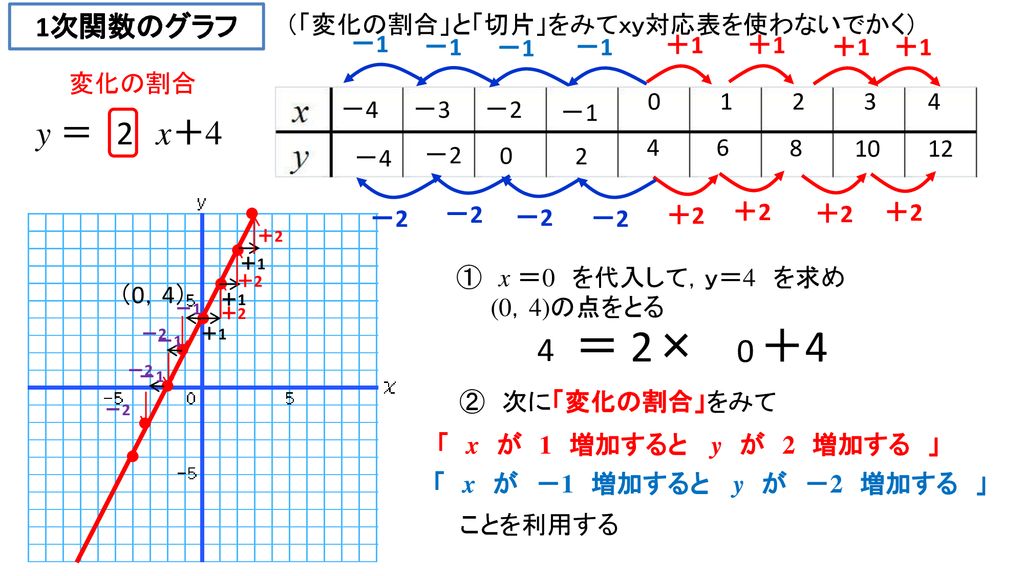
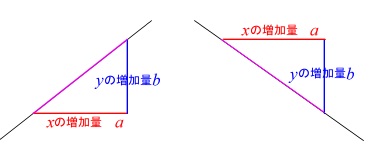
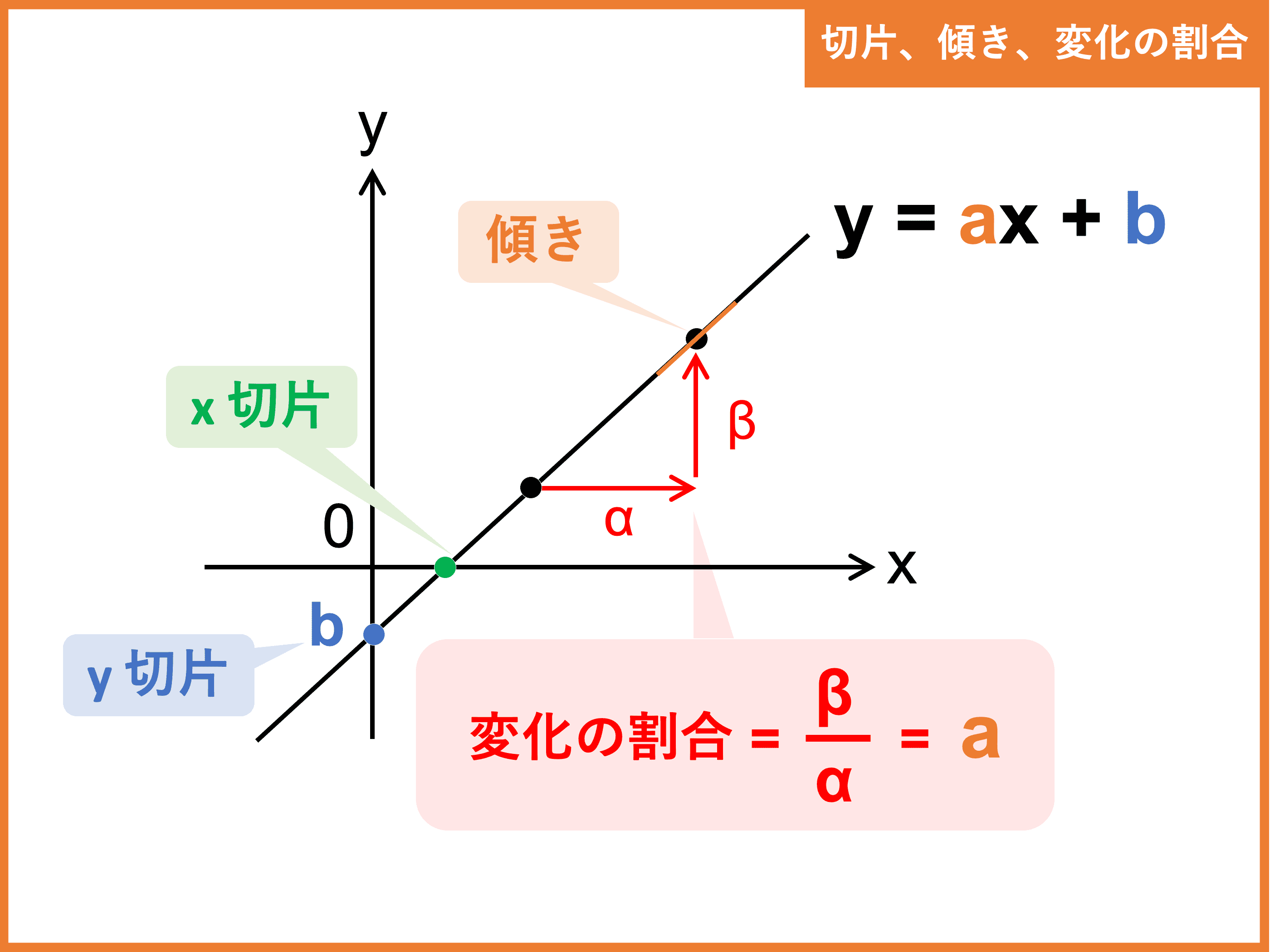
1次関数以外の関数を考えるときには、変化の割合(rate of change)、ないし平均変化率(average rate of change)という言葉を使います。中学では変化の割合、高校では平均変化率と呼ぶようですが、どちらも同じ意味です。. 103 2次関数(変化の割合) 2次関数の基本は102でおしまいです。 式からグラフと、グラフから式が大切だったね。 2次関数ではいれていきます。 今日は変化の割合。 変化の割合ってなんなんだっていう説明は後でします。 とりあえず求められるよう. 1次関数のグラフを示しました。 1次関数の式 y=axb 上式の「a」に当たるのが「変化の割合」です。下図をみてください。1次関数の傾きは途中で変化することがありません。よって変化の割合aも一定の値です。※2次関数になると変化の割合が一定でない可能.
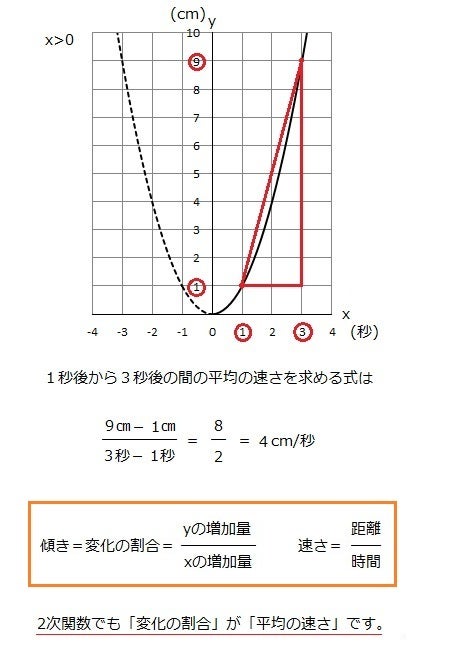
(2)(1)を用いて,関数 のxの値が4から2まで増加するときの変化の割合を求めなさい。 解説・解法 y=ax 2 の変化の割合の中でも少し応用編というか,発展編です。教科書には載っていませんが,この公式を覚えておいたら楽に点数が取れます。. というわけで、今回は中3で学習する関数\(y=ax^2\)の単元から 「平均の速さを求める」 についてイチから解説していくよ。 具体的には次のような問題のことだね。. \(y=ax^{2}\)の前に一次関数の例から考えていくので、「そもそも変化の割合ってなんだっけ? 」となっている人でも理解できると思います! また、 \(y=ax^{2}\)について や \(y=ax^{2}\)のグラフ について不安な方でも理解できるように、簡単な解説や詳しい解説.
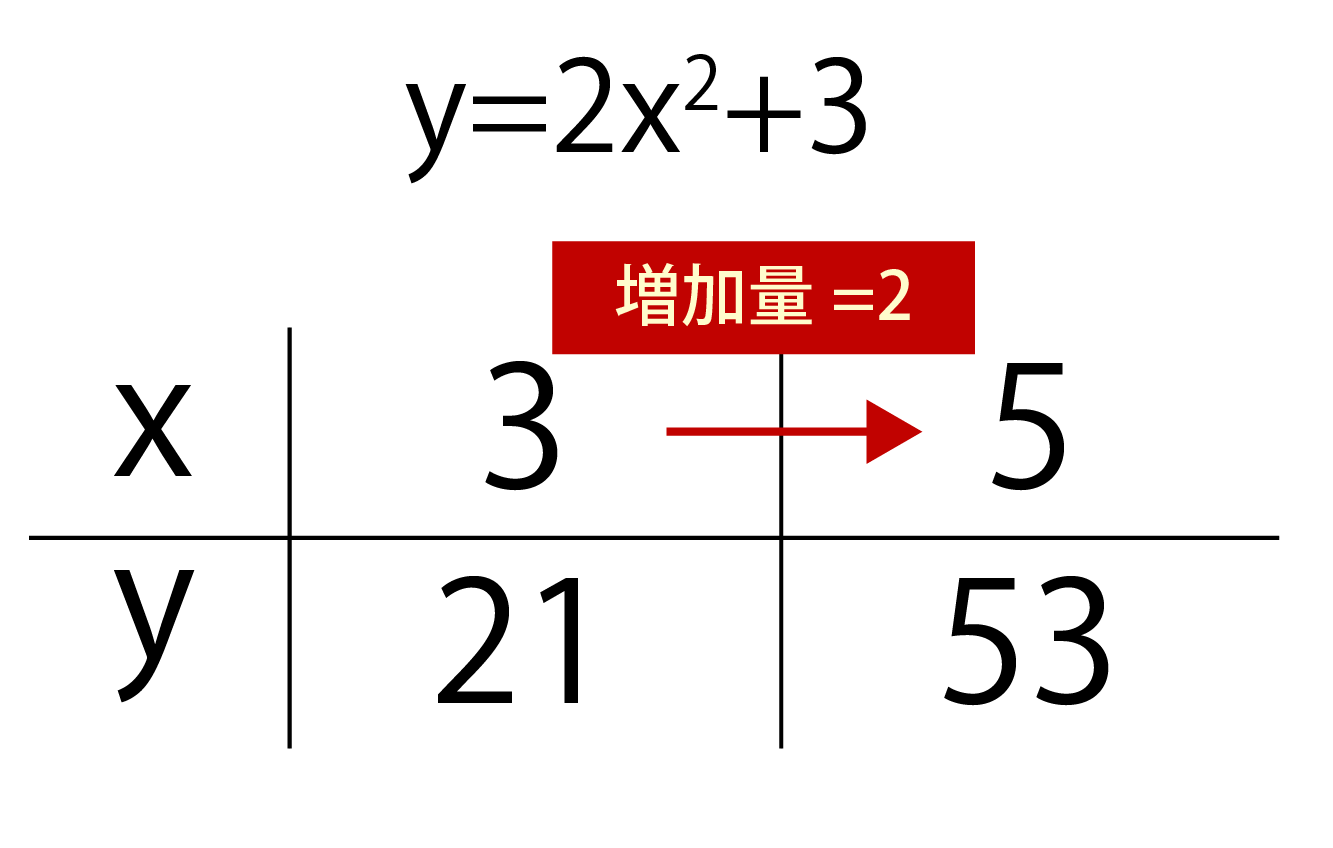
関数 \(y=ax^2\)について、\(x\)の値が\(m\)から\(n\)まで増加したときの変化の割合を考える。 基本形の解き方通りに考えてみると 表はこのようになります。. 2乗に比例する関数 変化の割合 2乗に比例する関数 変化の割合の問題です。 1次関数 y=axb では変化の割合がaで一定になります。 y=ax 2 の場合は 変化の割合は一定にはなりません 。 変化の割合は 例) y=2x 2 について ⑴ xが1から3まで変化するとき xの増加量=31=2 yの増加量=2×3 2 2×1 2 =16 変化の割合=16/2=8 ⑴ xが1から3まで変化するとき xの増加量=3 (1)=4 y. 変化の割合と交点 2次関数における変化の割合と、2次関数上の三角形の面積の求め方や2等分線について学習します。 変化の割合 三角形の面積 三角形の2等分線 変化の割合と交点 変化の割合と交点 変化の割合と交点 変化の割合と交点.
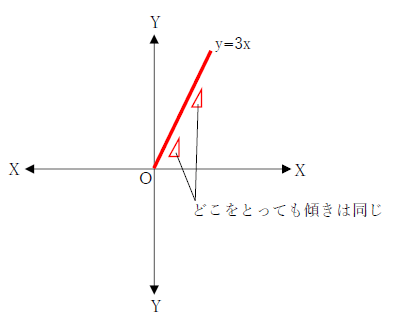
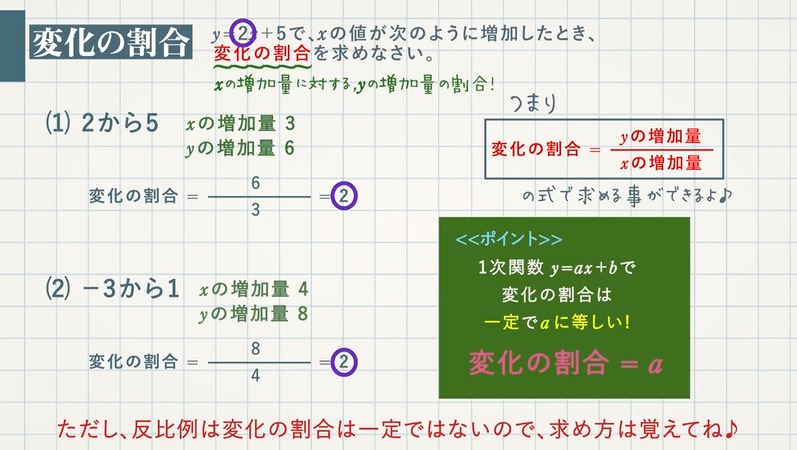
二次関数の変化の割合を求めたら一次関数の変化の割合も求まっているだけなんです。 しかし、なぜ二次関数の変化の割合はa 3 =a 1 (x 1 +x 2)で表されるのでしょうか? 公式だからといえばそれまでですが公式がなぜ成り立つのかを考えてみましょう。. ポイントの解説授業 今回のテーマは、「 変化の割合 」だよ。 1次関数y=ax+bにおいて、「変化の割合」が何を表すのか、先にポイントをおさえておこう。 POINT y=ax+bにおいて、「変化の割合」はa のことを指しているんだ。 つまり、 y= 2 x+1なら. 一次関数では、どの2点で結んでも直線上にあるため、グラフ自体の傾きは常に一定です そのため、変化の割合 (傾き)が変わることがなく、比例定数と同じという考え方が出来ました 二次関数では、結ぶ点により傾きが変わってくるため、変化の割合と.
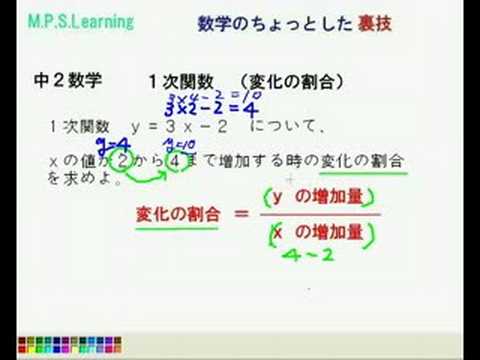
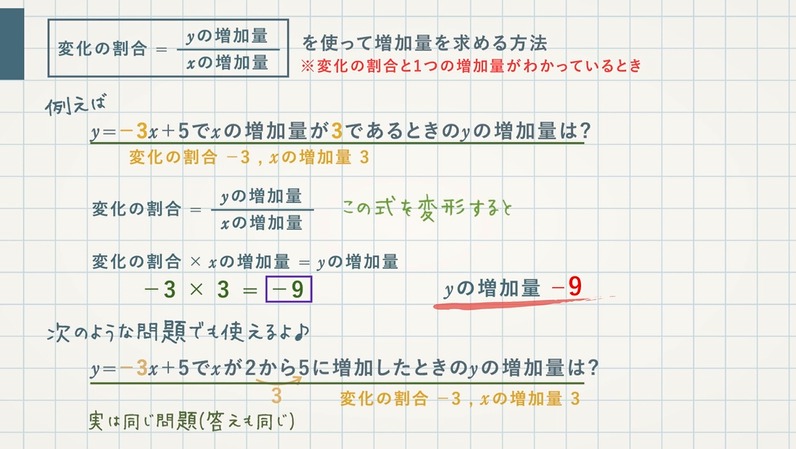
2次関数の場合、変化の割合の公式(変化の割合=yの増加量/xの増加量)を文字で置き換えて解くことによって、もう1つの公式を得るこことができましたね。 y=ax2でxがnからmまで増加するときの変化の割合は、 変化の割合=a(nm) となる。 スポンサーリンク 変化の割合 変化の割合=yの増加量/xの増加量 yの増加量=変化の割合×xの増加量 ちなみに、1次関数は、直線であり、. 変化の割合とは が増える量に対してがどれくらい増えるかを表したもの です。 この定義は一次関数においても二次関数においても変わりはありません。 つまり、 変化の割合の変化量 の変化量 少し数学的にいうと関数 において、 の値が から まで変化するとき、 の値は から まで変化します。 このときの変化の割合は になります。 以上が変化の割合の定義になります。 次からは一. 変化の割合を計算してみます。 x の増加量= 2-0 =2 y の増加量= 8-0 =8 ですから、 変化の割合= 8÷2 =4 このように、簡単に求められます。 そして、計算の結果、 この場合の「変化の割合」は 「4」 なので、 “a の値”とは違うものですね。 ですから、y=ax² では、 ・ “a”は「比例定数」とは呼べるが、 ・ 「変化の割合」とは言えない。 (⇒ 「変化の割合」 は、 計算しないと分からない 。.
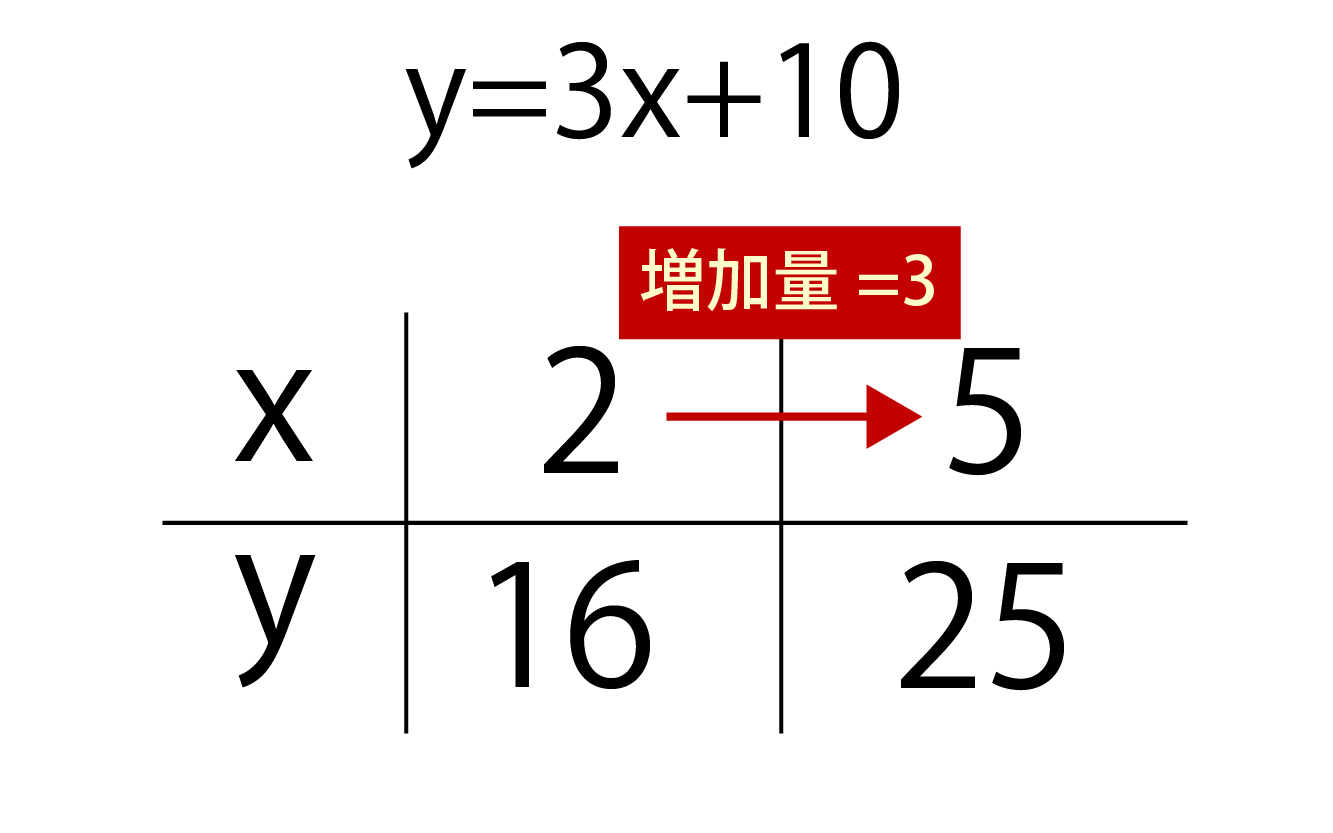
変化の割合は何を意味するか考える。 解法 まず、1次関数のときの変化の割合は何だったのか覚えていますか? 1次関数の式は「y=ax+b」で、x,yは直線上の点の座標を表し、aは傾き、bは切片を表. 二次関数の変化の割合の応用が分かりません。 問題文は以下の通りになります。 問、2つの関数y=-x^2、y=ax+1について xが-3から1まで増加したときの変化の割合が等しいという。 aの値を求めなさい。 私なりに式をa(-3+1)=-1と立ててa=二分の一と解. 変化の割合= yの増加量 xの増加量 比例反比例、1次関数、そして2乗に比例する関数、 変化の割合 はすべて同じ式を用いる。 ただし、1次関数では変化の割合は一定だが、 2乗に比例する関数では変化の割合は一定にならない。 y=3x2 についてそれぞれの場合の変化の割合をもとめる。 xが−3から1まで変化するとき xが1から5まで変化するとき ① xが3から1まで変化するときの変化の割合 x=3のとき.
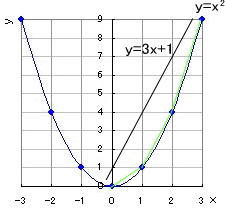
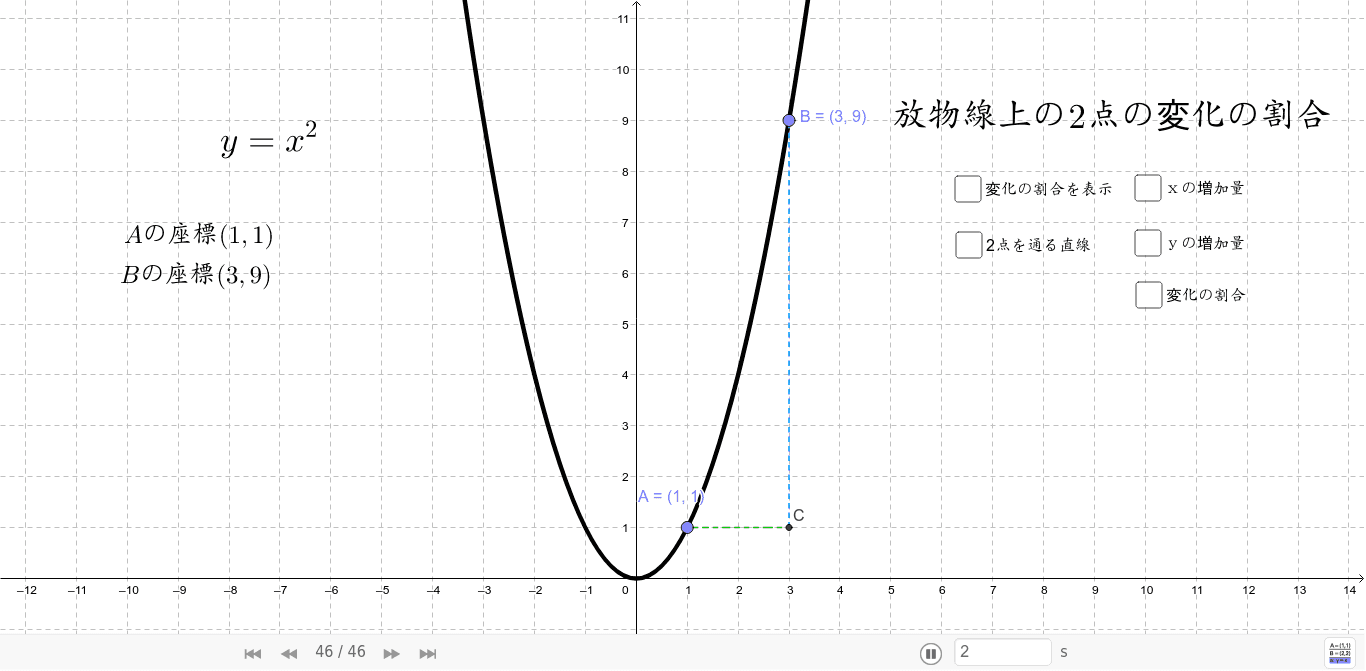
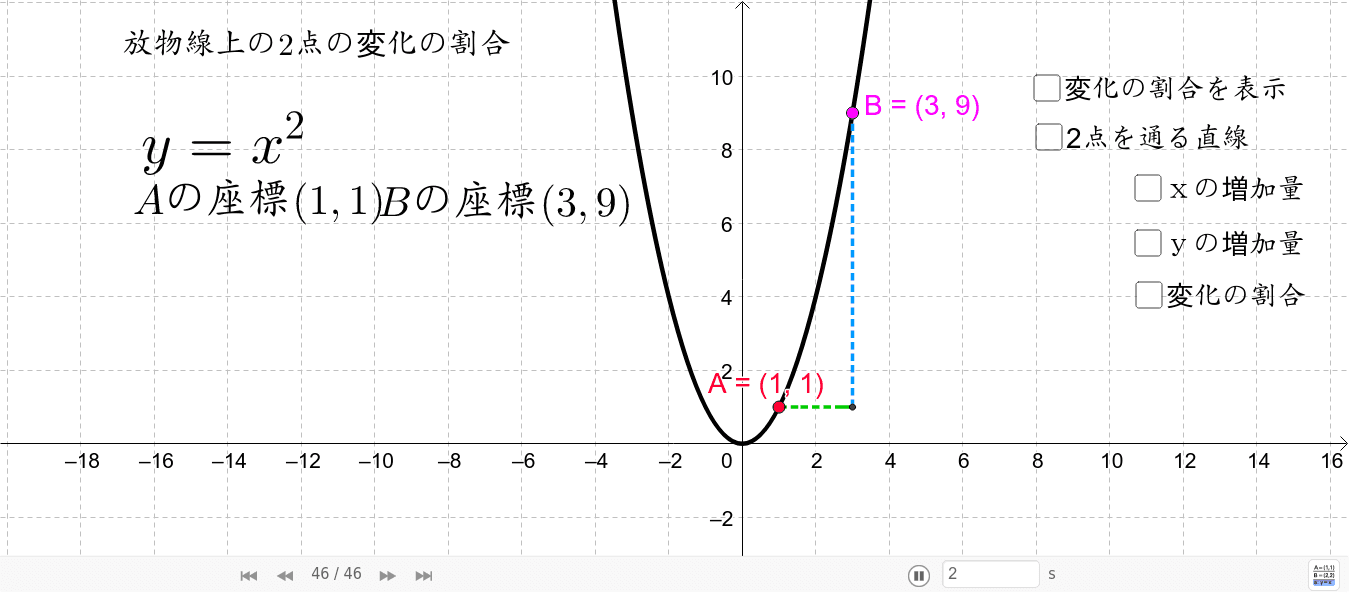
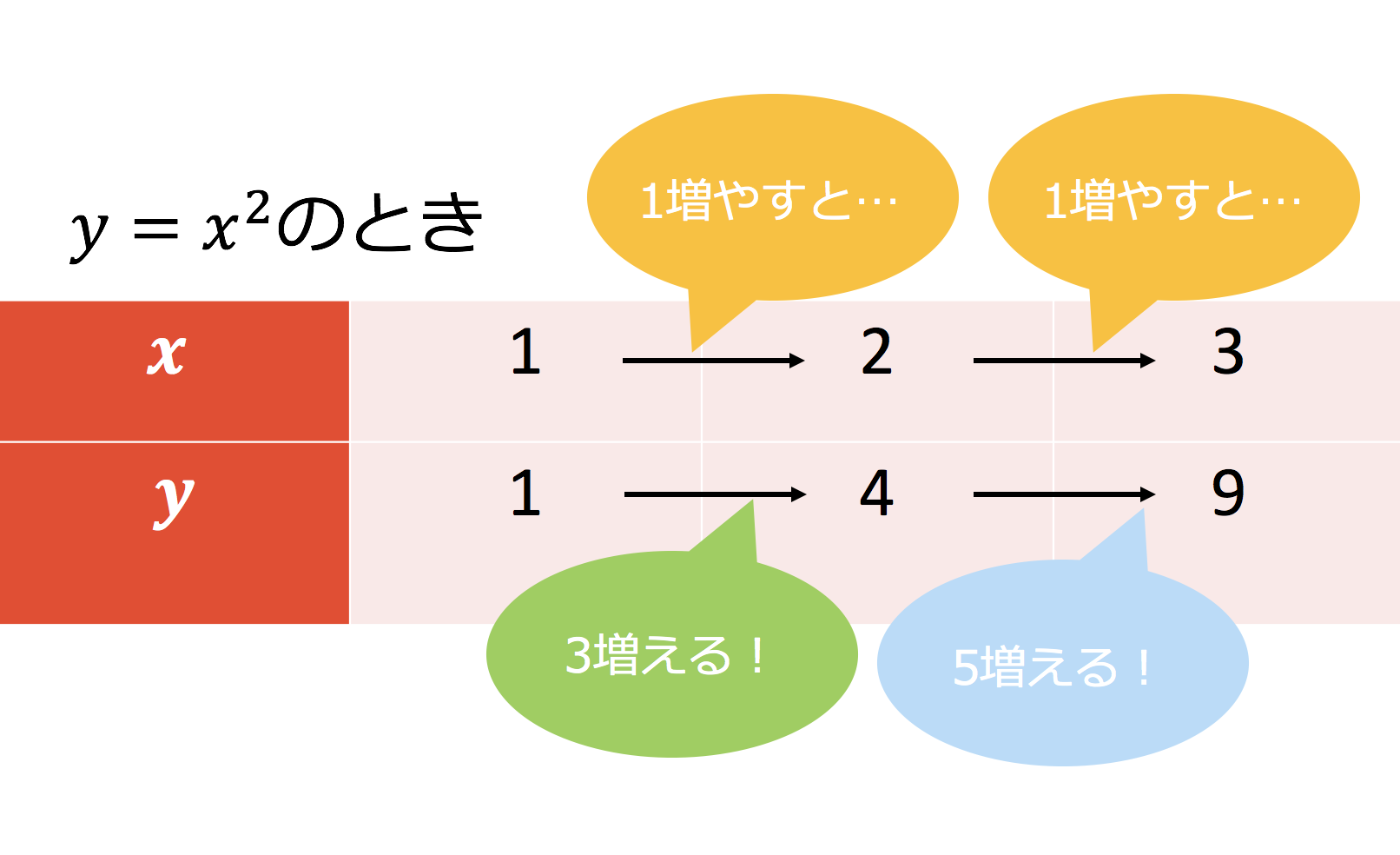
変化の割合のポイントは! 変化の割合とは、x の増える量に対して、y がどれだけ増えたかを示す割合で、( y の増加量 ) / ( x の増加量) で求める. 次の関数 y=x 2 (図1)においては,xが1から3まで変化するとき(xは2増加),yは1から9まで変化します(yは8増加). このとき,関数 y=x 2 の「変化の割合」は といいます. xの増加量=xの最後の値-xの最初の値=3-1=2 です.. 関数変化の割合の求め方まとめ! 変化の割合は、どんな関数においても $$変化の割合=\frac{yの増加量}{xの増加量}$$ これを使って求めることができるんだけど 一次関数は傾きと等しい。 二乗に比例する関数は \(a(pq)\) で求めれる。.
新しい関数として 「 = y = a x 2 」を 学習しましたね 中3数学「関数 = y = a x 2 」の問題 どこよりも簡単な解き方・求め方 「関数」は、中1で「比例」、中2で「一次関数」を学習しましたね 中3では「2乗に比例する関数」を一緒に見ていきましょう. 「変化の割合」が求められます。 同じく、y=2x² で、 xが 「-3から-1まで」 増加するときの 変化の割合は ⇒ 2×{(-3)+(-1)} = -8 ほら、あっという間ですよね! ちなみに、 こうして求めた「8」「-8」が 正解であることは、 こちらのページ と、もう一度比べれば すぐ分かります。 先ほど見てもらった同じ記事ですが、 y=2 x² で、 x が「1から3まで」増加するとき y=2 x² で、 x. 放物線の変化の割合 \(1\) 次関数の変化の割合は常に一定で比例定数に等しくなりますが、\(2\) 乗に比例する関数では、変化の割合は一定ではありません。 そのことは、変化の割合を求める公式より明らかになります。 関数 \(\boldsymbol{y=ax^2}\) の変化の割合.
二次関数y=ax2の変化の割合の求め方 には公式があるよ。 xの値がmからnまで増加するとき、変化の割合は、 a (mn) になるんだ。 つまり、 (比例定数)×(xの小さい値 xの大きい値) っていう計算。 簡単だ! さっそく、この公式で変化の割合を求めて. 2次関数の変化の割合とは? 復習になりますが、変化の割合とは \(x\)に対して\(y\)がどれだけ変化するかを表す値 です。 「\(x\)が1増えた時の\(y\)の増加量」、具体的には「\(\dfrac{yの増加量}{xの増加量}\)」です。 1次関数の場合、変化の割合は常に一定なので、『傾き=変化の割合』でした。. 1次関数について質問があります。 変化の割合が6で、x=0のときy=2となる1次関数の式を求めなさい。 答えはy=6x2となるようですが、考え方を教えて下さい。 ご回答お願いします。.
二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

2次関数と変化の割合 基 標 数学の解説と練習問題

二次関数のグラフでは変化の割合が一定ではないと思うのですが 写真のように求め Clearnote
2 次 関数 変化 の 割合 のギャラリー

1次関数の変化の割合 Youtube

無料 中3数学 発展 応用問題 問題プリント 323 関数y ax2乗 4変化の割合

数学 中学3年生 二次関数の変化の割合 傾き の求め方のコツ なるほど 塾講師が教える教え方のコツ
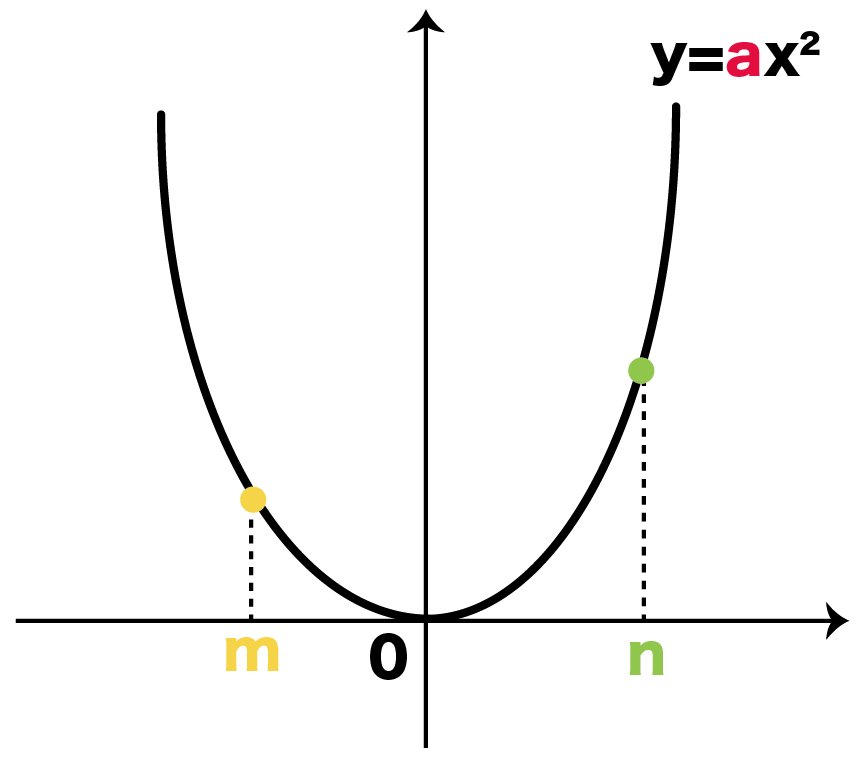
二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

Mathematics 2次関数 2乗に比例 の 変化の割合 を簡単に求める方法 働きアリ

変化の割合 Twitter Search Twitter

この問題がわからないので解説お願いします Clearnote

中2数学 変化の割合 映像授業のtry It トライイット

変化の割合 清水塾

中学3年数学 変化の割合の計算 交点の座標 練習問題1 あんのん塾

Y Ax2乗の利用 平均の速さの求め方は変化の割合と同じだ 中学数学 理科の学習まとめサイト

中学3年の数学 動画 二次関数の変化の割合の問題 19ch

中3数学 二次関数10 変化の割合 A P Q すべて無料 星組の中学数学講座
1次関数のグラフ テーマ 目的 xyの対応表を使って 考えられるすべての点をうってグラフをかく以外に 変化の割合を使ってグラフをかく Ppt Download
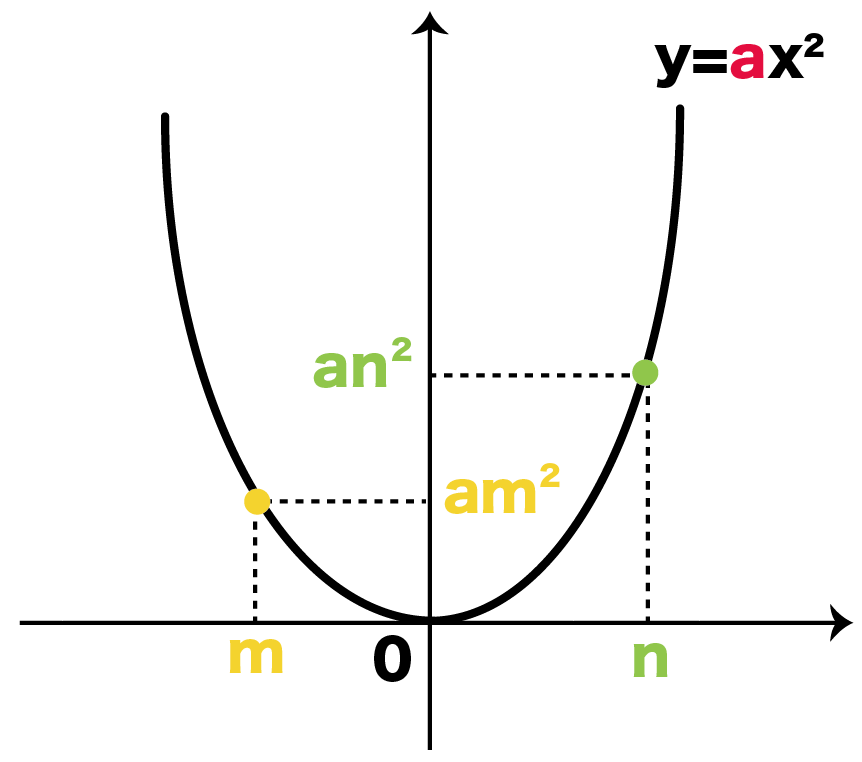
二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
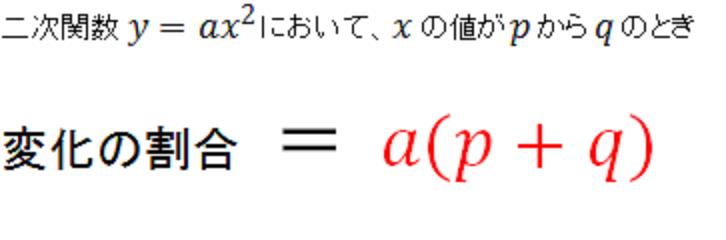
8月23日の授業日記 中3一斉授業 2次関数の変化の割合 裏ワザあり 成績 上がってます 根城学習塾 八戸市
数学3 二次関数 変化の割合と直線の傾き Geogebra
写真ような場合なぜ一次関数は問題の8が変化の割合として扱えるのに二次関数は 1 Yahoo 知恵袋

数学 中2 29 変化の割合 Youtube

平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ

二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
変化の割合とは 1分でわかる意味 公式 傾きと増加量との関係
1

一次関数 一瞬で答えられる変化の割合 苦手な数学を簡単に

2次関数と1次関数の変化の割合の問題 Youtube

2次関数 変化の割合 清水塾
2

2次関数の基本
中3数学q 二次関数の傾きがいちばん大きいものは この写真の通り Yahoo 知恵袋
中学数学 Y Ax 2 変化の割合の意味 中学数学の無料オンライン学習サイトchu Su
変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ
変化の割合とは 1次関数の求め方と直線の方程式との違い

2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun
変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ
平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ
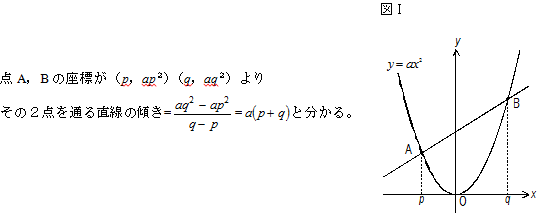
開成ハイスクールブログ ブログアーカイブ 2次関数から微分 積分へ

中3数学 二次関数 𝑦 𝑎𝑥 と 𝑦 3𝑥 の変化の割合が等しくなるときの 𝑎 の値 Youtube

1次関数の表から変化の割合 Geogebra

変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ
2次関数 変化の割合 中学から数学だいすき

変化の割合を求める 1次関数 あんず学習塾のメモ 図表置き場

1次関数の式の出し方

1次関数の公式 変化の割合の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

数学 学校では教えてくれない1次関数の裏技 中学生 数学のノート Clearnote

変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ

2次関数 変化の割合

2次関数 変化の割合 簡単な求め方 学習内容解説ブログ

10 3 2次関数 変化の割合 勉強できようサイト
中2数学 1次関数 変化の割合 Youtube

2乗に比例する関数 変化の割合 無料で使える中学学習プリント

1次関数の値の変化 増加量と変化の割合 教遊者

中3 中3数学 2次関数 変化の割合のまとめ 中学生 数学のノート Clearnote

中3数学 二次関数の変化の割合の定期テスト過去問分析問題 ダイスト
二次関数とは 公式や 最大値 最小値 決定の問題の解き方 受験辞典

1次関数の値の変化 増加量と変化の割合 教遊者

変化の割合とaの値の違いってなんですか Clearnote

2次関数 変化の割合 Youtube
関数とは 意味や用語 切片 変化の割合 傾き を簡単に解説 受験辞典

変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ

10 3 2次関数 変化の割合 勉強できようサイト
1
二次関数の変化の割合 Geogebra

4の 1 変化の割合の求め方教えてください 4の 1 変化の割合の求め方 中学校 教えて Goo
3
2乗に比例する関数 変域 変化の割合

数学 中3 38 二次関数の変化の割合 Youtube

中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学

一次関数変化の割合も み は じ みたいなやつで 都立入試の情報満載 こじんまりしたこじま塾ブログ

10 3 2次関数 変化の割合 勉強できようサイト

変化の割合の求め方 一次関数と二次関数の変化の割合を求めよう 中学や高校の数学の計算問題

二次関数の変化の割合をスッキリ求めたい 去年の今日日記 都立入試の情報満載 こじんまりしたこじま塾ブログ

みらい塾 二次関数の変化の割合にこんな公式があるのを知ってましたか 時間短縮に役立つので使ってみてください
1次関数の値の変化 増加量と変化の割合 教遊者

Mathematics 2次関数 2乗に比例 の 変化の割合 を簡単に求める方法 働きアリ The 2nd

2次関数 膨大なページ数 Wiki

関数y Ax2乗 変化の割合の裏ワザ公式 どうやって解くの Youtube

中学数学の問題倉庫 おしゃれまとめの人気アイデア Pinterest West Heroes 21 中学数学 数学の問題 数学

中3数学 二次関数9 変化の割合 すべて無料 星組の中学数学講座

y ax2の変化の割合の求め方 基本と裏ワザ 現役塾講師のわかりやすい中学数学の解き方
二次関数についてです 二次関数は変化の割合が一定では無いのに Yahoo 知恵袋
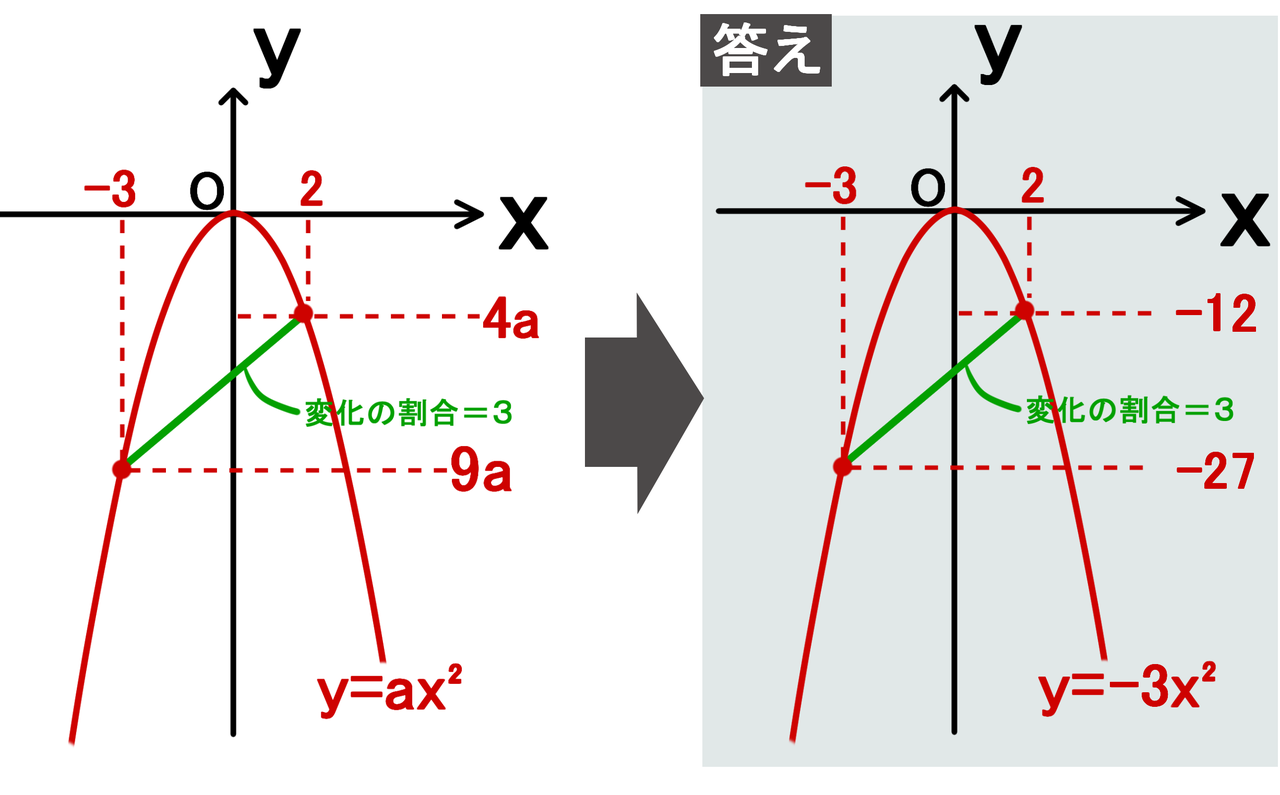
関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
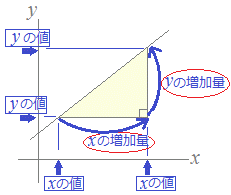
変化の割合

1次関数 板書

1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場

中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学
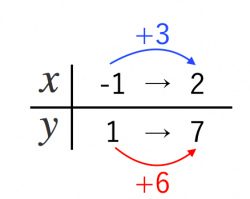
一次関数 知らないとできない変化の割合 苦手な数学を簡単に

Tossランド 1次関数の値の変化

数学 中学3年生 二次関数の変化の割合 傾き の求め方のコツ なるほど 塾講師が教える教え方のコツ

中3数学 Y Ax 2の変化の割合 例題編 映像授業のtry It トライイット

変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ

変化の割合 無料で使える中学学習プリント
1

変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ
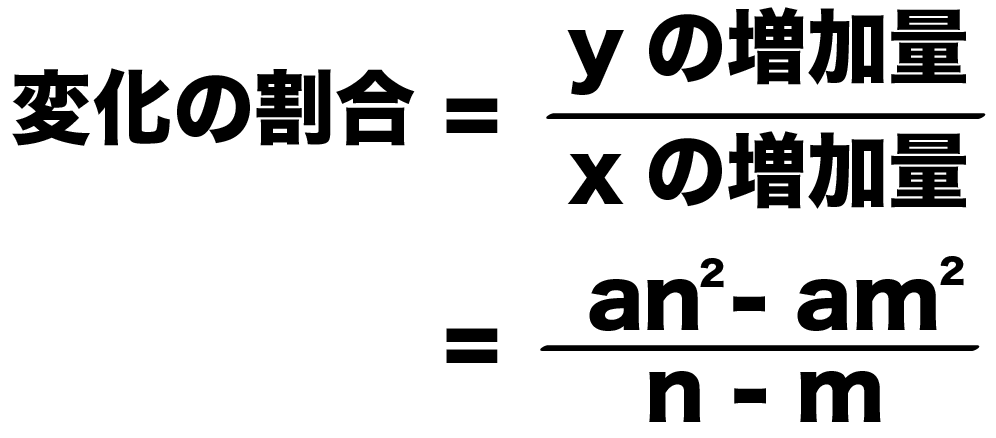
二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

変化の割合 簡単な求め方は 一次関数 二乗に比例する関数のやり方 数スタ
1次関数の値の変化 増加量と変化の割合 教遊者

変化の割合 Xの変化量分のyの変化量 を使えるのって二次関数の時だけですか Clearnote
二次関数の変化の割合 Geogebra
3分で分かる 変化の割合とは 意味やその求め方をわかりやすく 合格サプリ
二次関数についての質問です 関数y X の値が次のように増 Yahoo 知恵袋




