三角形 の 相似 条件 証明
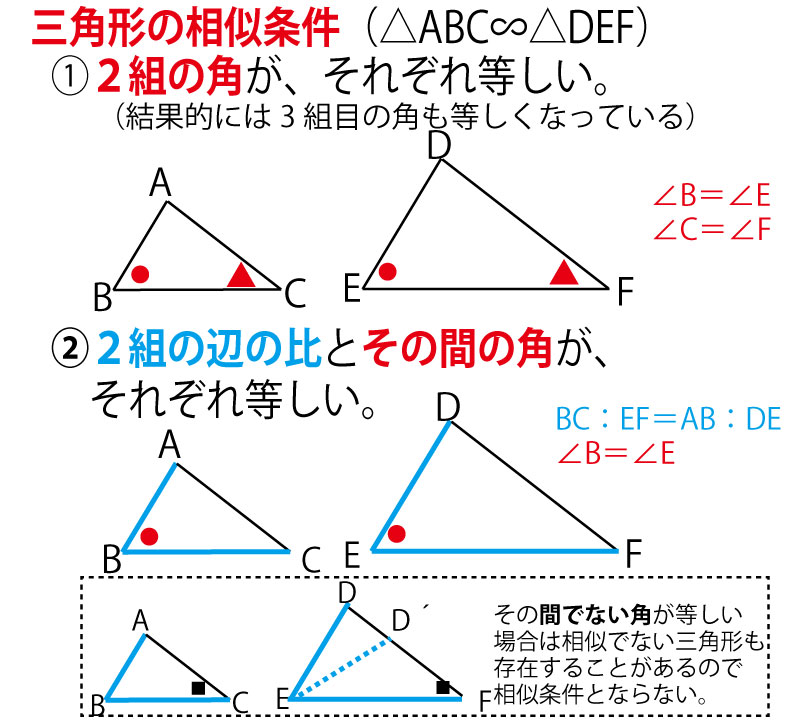
三角形の相似条件 三角形の相似を証明するためには、「相似条件」というものを使います。 相似条件には、以下の \(3\) つがあります。 相似条件①3 組の辺の比がそれぞれ等しい \(3\) 辺の比がそれぞれ等しければ、相似と言えます。.
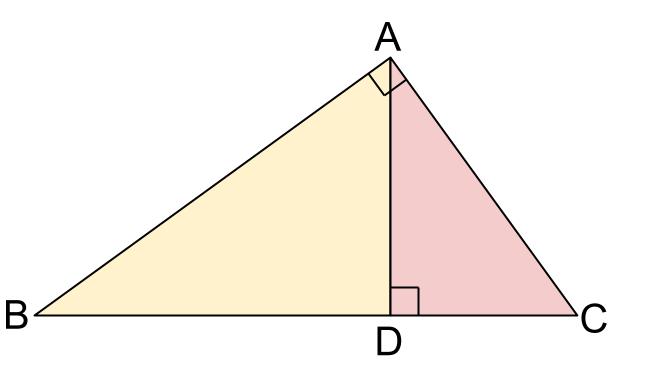
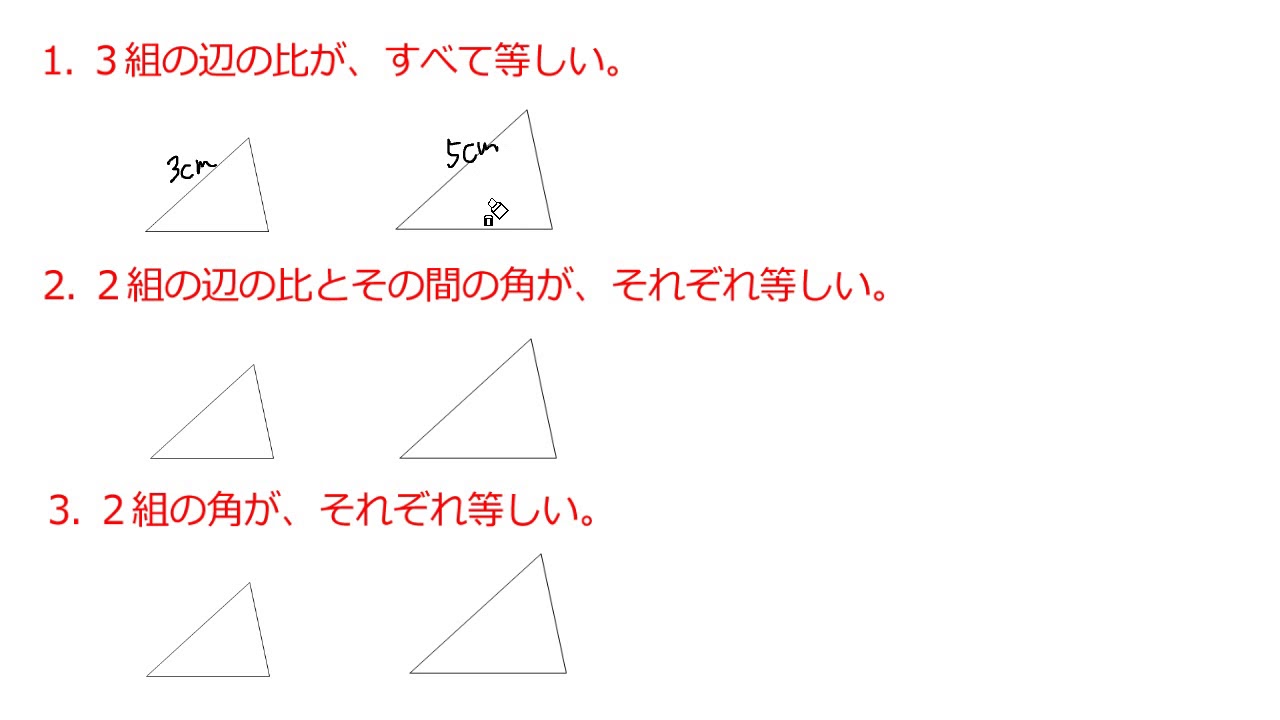
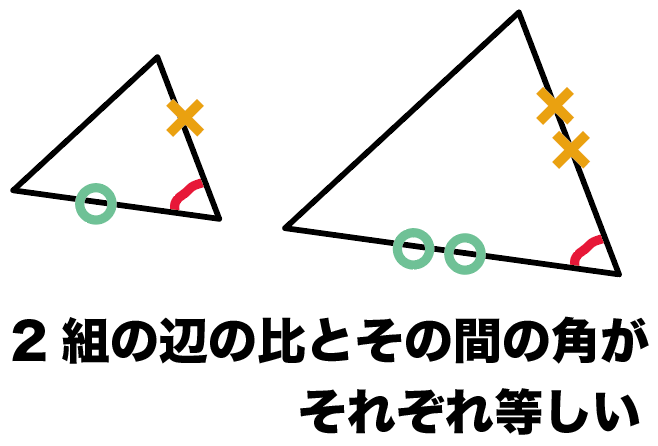
三角形 の 相似 条件 証明. パワーポイント教材(1280k) ワークシート 学習指導案 new!. 三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」が. 中に引いた線が平行ならば、 ⇒ 「共通の角と、同位角」 で “2組の角” がそれぞれ等しい ・平行でなければ、 「共通の角」 & 辺の長さをチェックして ⇒ “2組の辺の比とその間の角” がそれぞれ等しい この流れで、相似を証明できます。 これで、 相似な三角形の「見つけ方」 について、 パターンとコツが見えましたね。.
三角形の成立条件の証明(必要性) 「三角形が成立する→三角不等式が成立する」を証明します。 寄り道した方が距離が長くなる という直感に従うと自明ですが,一応きちんと証明してお. 相似に関係した 定理, 証明などを掲載します。 三角形の相似条件,平行線と線分比の関係,中点連結定理,台形の中点連結定理,扇形(おうぎ形) と展開図による表面積と,体積の比。. 三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件を確認していき.
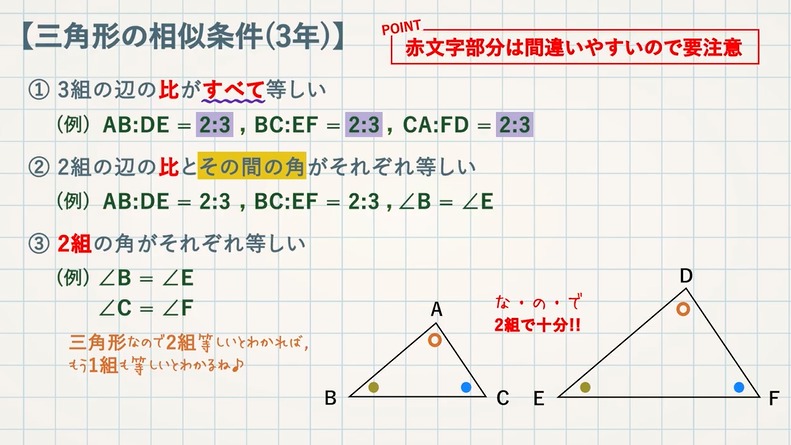
三角形の相似条件と基本的な証明 三角形の相似条件と三角形の相似条件を使った証明問題です。 相似条件を使って相似な三角形を見つけるのは、応用問題や入試問題でよく出題されるので、しっかり出来るようにしてください。 三角形の相似条件は2年生で習った三角形の合同条件と似ていますが、相似は図形を拡大、縮小したものなので、辺の比が等しい. 三角形の相似条件( $3$ 年) ① $\textcolor{blue}{3}$ 組の辺の比がすべて等しい (例) $\textcolor{blue}{\rm ABDE=23}$ , $\textcolor{blue}{\rm BCEF=23}$ ,. ・ 角形を見つけ、証明の仕方を知る。 三角形の相似条件を適 の相似条件を確認してから、証明問題に取り組む 言葉や式を使って表して 6 切に使って、説明を書 ようにする。 いる。 相似な三角形を見つけて、その根 くことができる。.
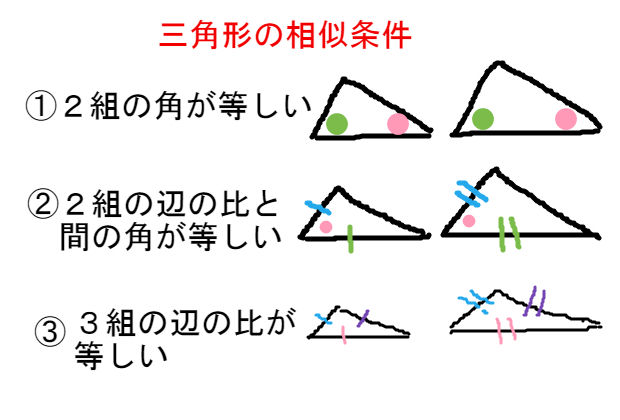
また、問題の解き方も簡単に解説していくので、ぜひこの記事を通してマスターしてくださいね! 目次 非表示 中点連結定理とは? 中点連結定理の使い方例題 中点連結定理の証明 証明①三角形の相似を利用 証明②平行四辺形の性質を. 「図形の中から相似な三角形を見出し、相似条件を用いて証明することができる。 2つの三角形は、次のどれかが成り立てば相似である。 ① 3組の辺の比が等しい。. 三角形の相似条件 「三角形の合同条件」は、「形」も「大きさ」も同じというための条件。 「三角形の相似条件」は、「形」さえ同じであればよいという条件ですので、 「合同」より条件がゆるいですね! もう少し正確に言うならば、.
>三角形の相似条件、合同条件を証明して下さい。 「~条件」を証明するってことですよね。 条件を証明することはできるのですかね? そうではなくて、 例えば、合同条件の1つである「2組の辺とその間の角がそれぞれ等し」ければ合同である。. <前:L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答:次> 練習問題1 以下の1~3に示した各組の三角形が相似であることを証明しなさい。 (※辺の長さの単位はcm). 三角形の合同の証明① 下の図で,ab=ac,−bad=−cad である。このとき,¼abd×¼acd で あることを右のように証明した。下線部 をうめて,証明を完成させなさい。 三角形の合同の証明② 下の図で,am=cm,bm=dm であ る。このとき,ab=cd であることを右.
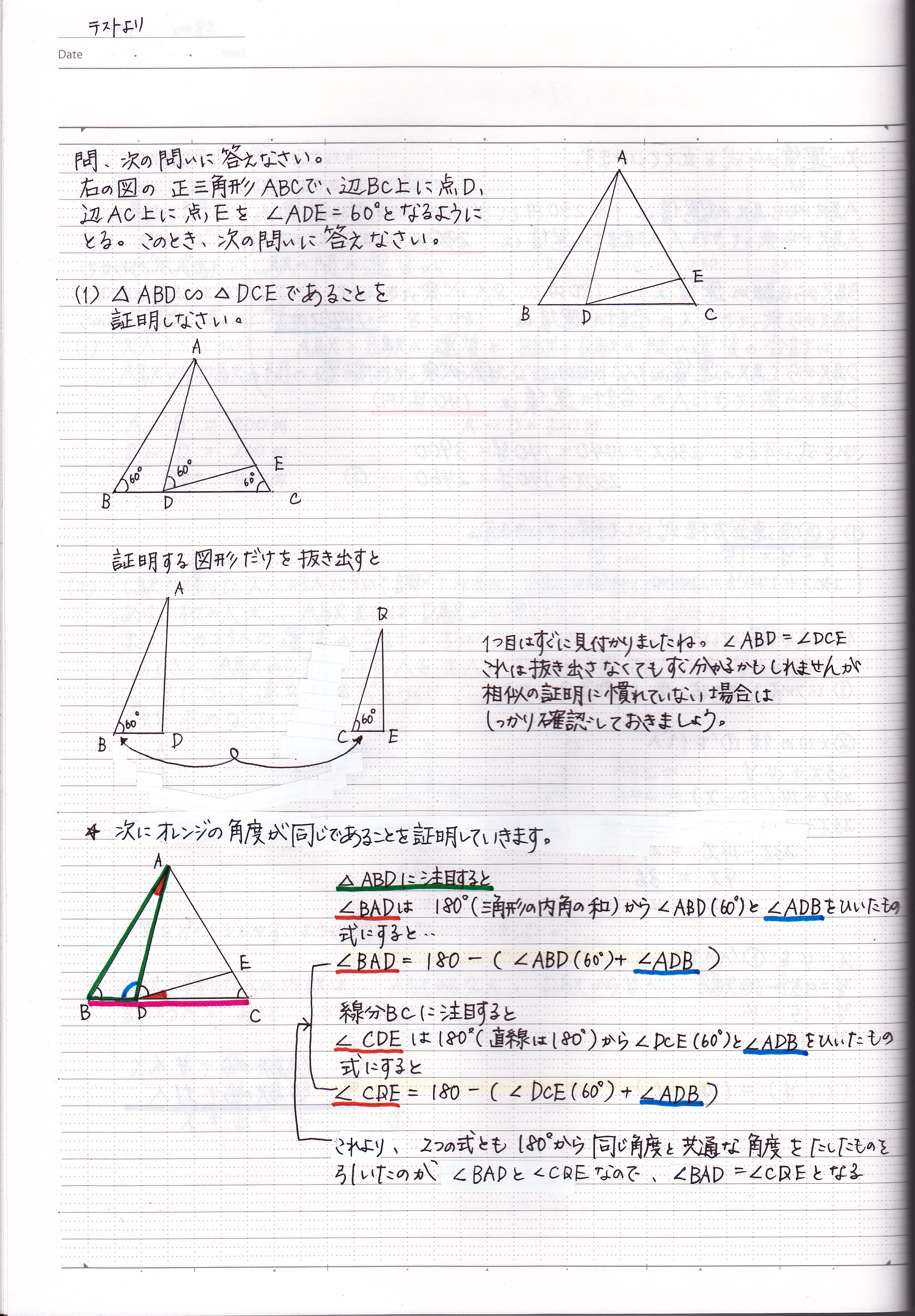
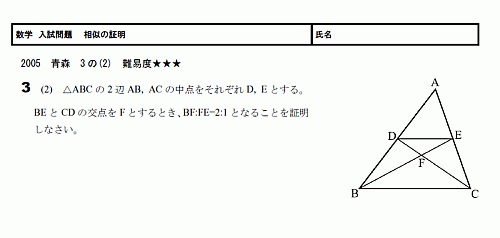
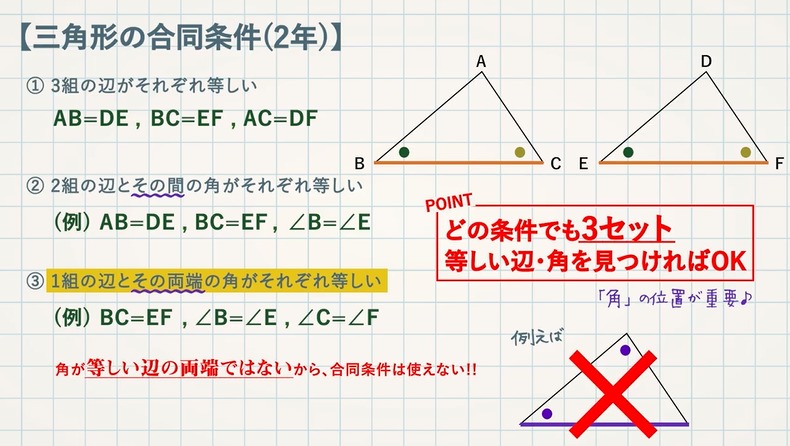
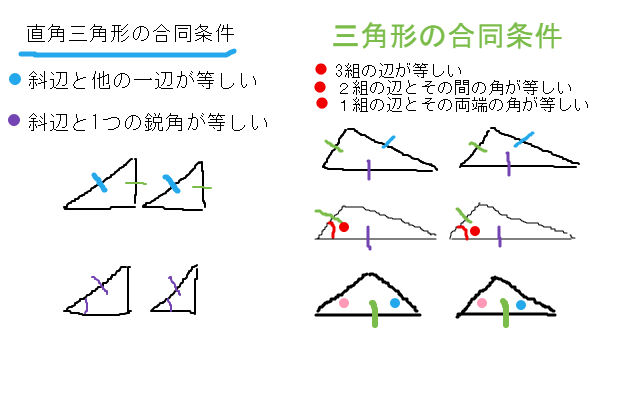
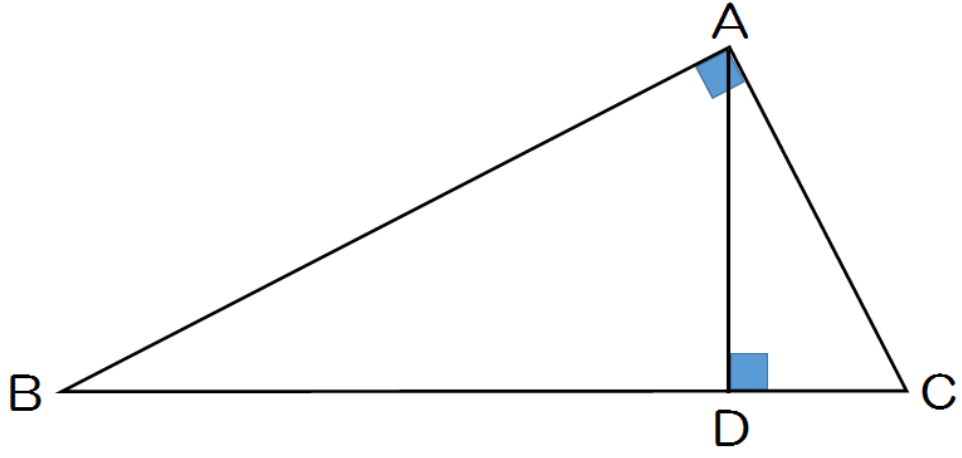
第5章 図形と相似 <前: L31 三角形の相似条件と証明 の問題 L32 縮図の利用 の問題 :次> 練習問題1 以下の1~3に示した各組の三角形が相似であることを証明しなさい。 (※辺の長さの単位はcm) 1 ABCと EDC ≪答≫ ABCと EDCにおいて、 仮定. 相似の証明1 図の ABCは∠BAC=90°の直角三角形である。 頂点Aから辺BCに垂線を下ろしその交点をDとする。 A B C D ABD∽ CBAを証明せよ。. 三角形の「合同条件」と「相似条件」 を勉強してきたよね。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件.
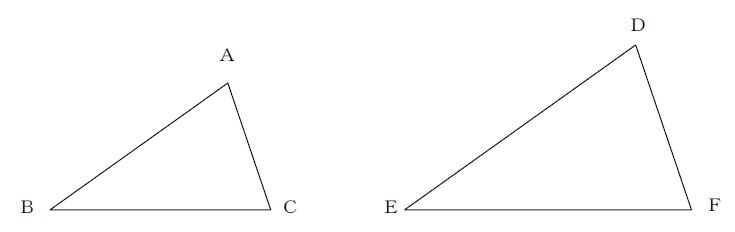
この3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている ABCと ABDが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめていきます. このように三角形の相似条件 (ア)2辺の比とその夾角が等しい (イ)2角が等しい などもうまく説明(証明)できないでしょうか? よろしくお願い致します。. 相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載.
三角形の相似条件 中3数学 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99%「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。. 三角形の相似の証明 中学2年で学習した、三角形の合同の証明とほぼ同じです。 用いるのが合同条件ではなくて、相似条件になっただけです。 三角形の合同の証明があやふやな人は、そこから学習をしましょう。 急がば回れです。 証明. 三角形の相似 条件を用いた 証明の進め方 を理解してい る。(練習問題 の解決状況の 分析) 7 2.2つの三角形が相似である ことを、使う相似条件の見通し をもって証明することができ る。 見出した図形の 性質を根拠とし て、三角形の相似 条件を用いて相.
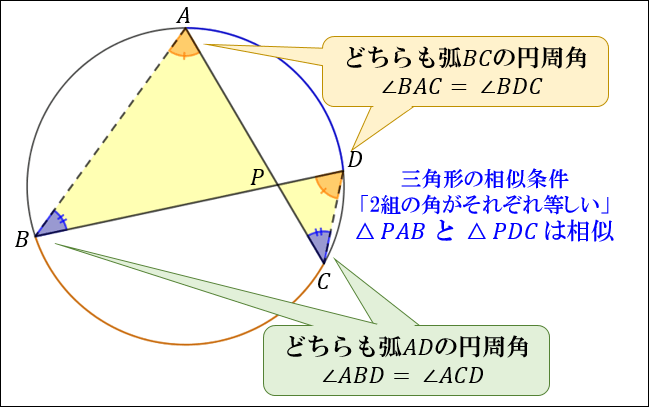
三角形の内角が、円周角になっている図形配置は非常によく出題されます。 このとき、 2 2 つの三角形の相似を証明するために用いる相似条件は ほぼ間違いなく 「 2 2 組の角がそれぞれ等しい」 です. つぎは、 相似な三角形 をさがそう。 三角形の相似条件にあてはまる2つの三角形をさがせばいいのさ。 念のため、三角形の相似条件を確認しておくと、 3組の辺の比がすべて等しい;. ・ 三角形の相似条件を用いて証明することができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学的活動をともなう学習活動).
三角形の相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方

中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su
方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
三角形 の 相似 条件 証明 のギャラリー

無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明

中3 相似 証明問題について どうも こんばんわ こんにちは 早速ですが Okwave

三角形の合同条件 相似条件と合同条件の違いとは アタリマエ

中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室
Ppt 相似条件と証明 Powerpoint Presentation Free Download Id
中3数学 線分の比と相似比の定期テスト過去問分析問題 ダイスト

中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学

三角形の相似条件と証明問題の解き方 数学fun
証明 合同 相似 が苦手な人へ 教遊者
図形と証明 相似 スタディーx

相似条件 合同条件 中学生 数学のノート Clearnote
相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス

三角形の相似条件と基本的な証明 無料で使える中学学習プリント
中学数学 相似の証明について質問です Abc Adeは正 Yahoo 知恵袋

都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法
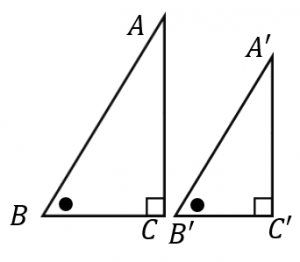
直角三角形の相似条件 具体例で学ぶ数学
三角形の相似条件 Youtube

中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく
図形と証明 相似 スタディーx

中3数学 三角形の相似条件1 3辺の比 練習編 映像授業のtry It トライイット

17年10月30日 数学 三角形の相似条件 オンライン家庭教師 ウェブリー

中学数学 図形の相似

5章1節2 三角形の相似条件2 数学のすすめ

中学3年数学 相似条件を使った証明 2学期期末テスト 赤城 ᐡᐤᐡ

数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
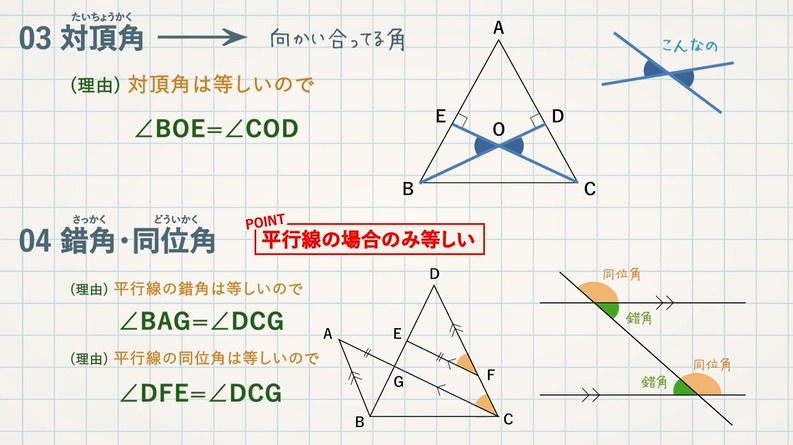
証明 合同 相似 が苦手な人へ 教遊者

数学 中3 44 三角形の相似条件 Youtube
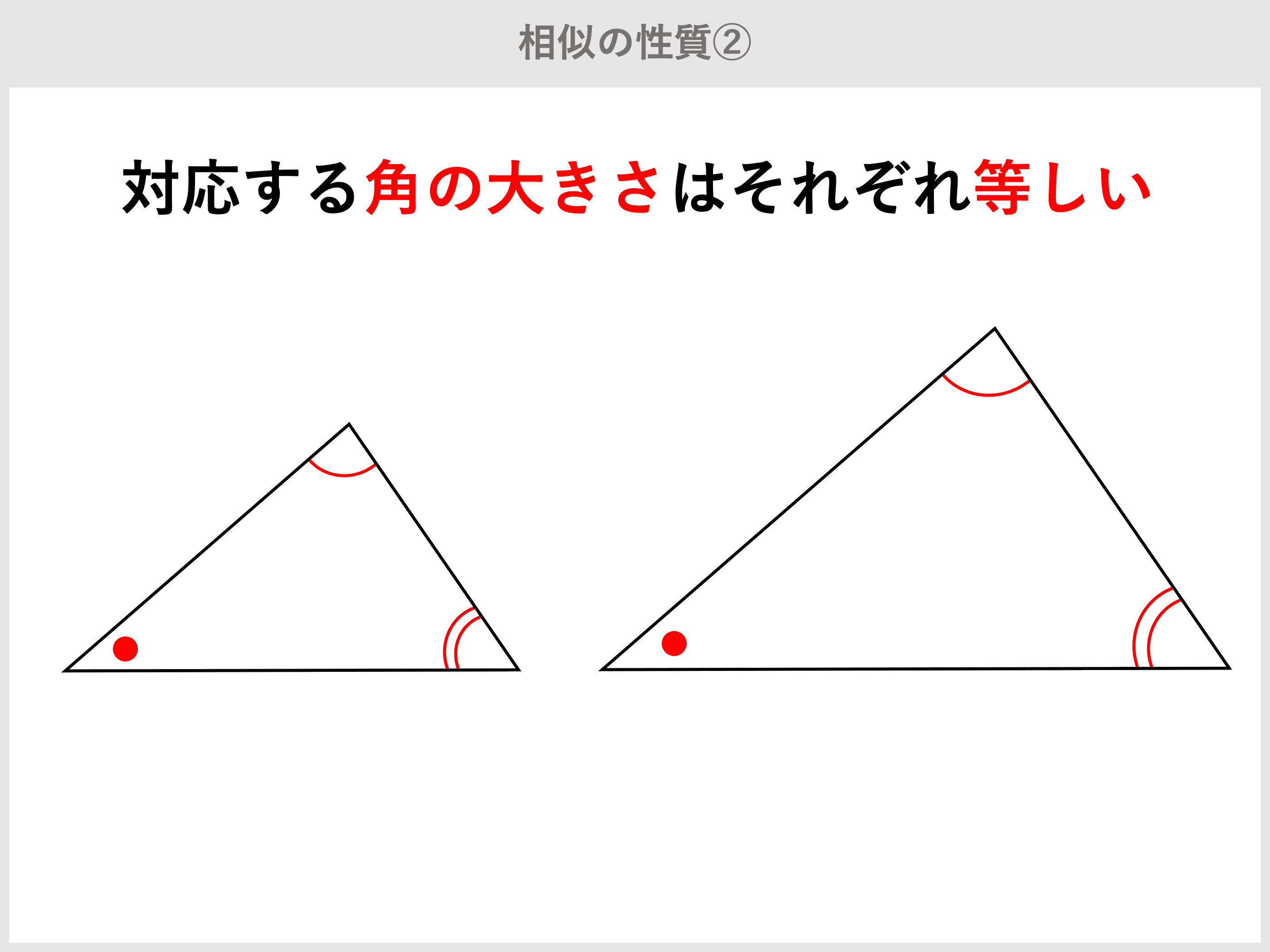
相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典

いろいろな相似の証明 無料で使える中学学習プリント

三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題
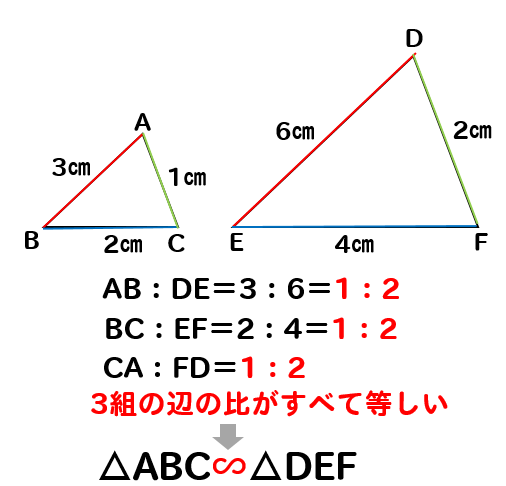
中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ

中3数学 相似の証明のポイントと練習問題
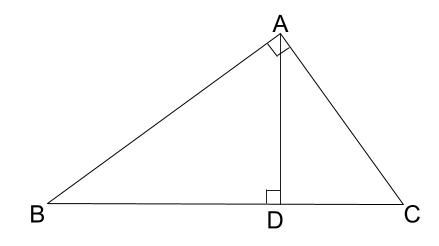
中学数学 相似の証明 その2 中学数学の無料オンライン学習サイトchu Su
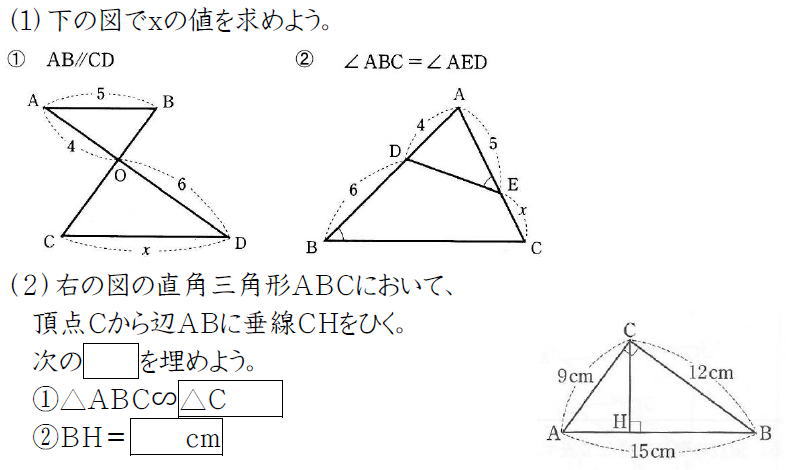
Studydoctor相似な三角形の辺の比 中3数学 Studydoctor
1
証明 合同 相似 が苦手な人へ 教遊者

中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト
相似と相似の条件を知ろう 数学の要点まとめ 練習問題一覧
三角形の相似 合同条件 中学 数学 理科の復習サイト
栃木県総合教育センター 算数 数学 学びの杜 中学校3年生 数学 三角形の相似条件と証明
三角形 合同 相似条件 直角三角形の合同条件 中学 数学 理科の復習サイト

数学 中3 46 相似の証明チャレンジ Lv 1 Youtube

直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
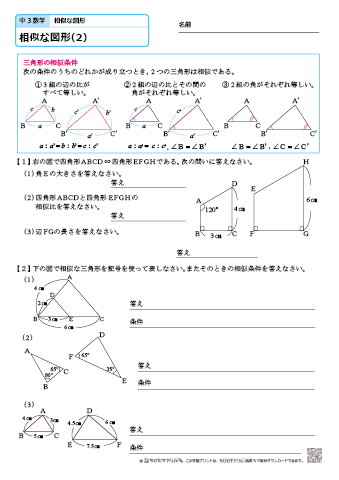
中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
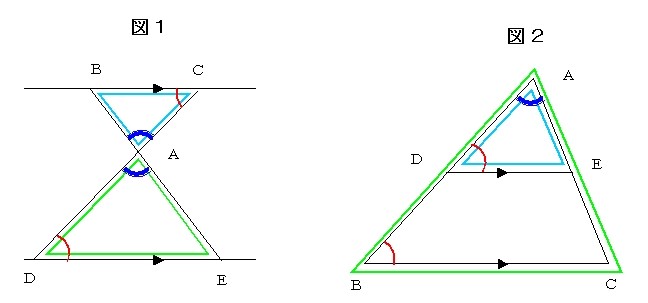
相似 直角三角形
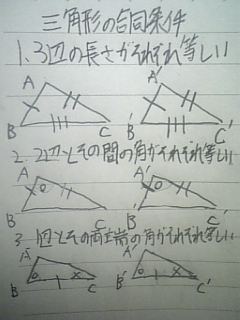
受験数学かずスクール 08年08月
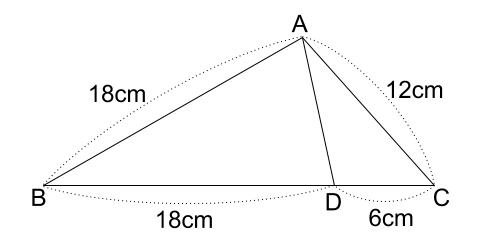
中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su
数学 相似条件と証明 について 下の図 写真 で Abcは Ab Yahoo 知恵袋
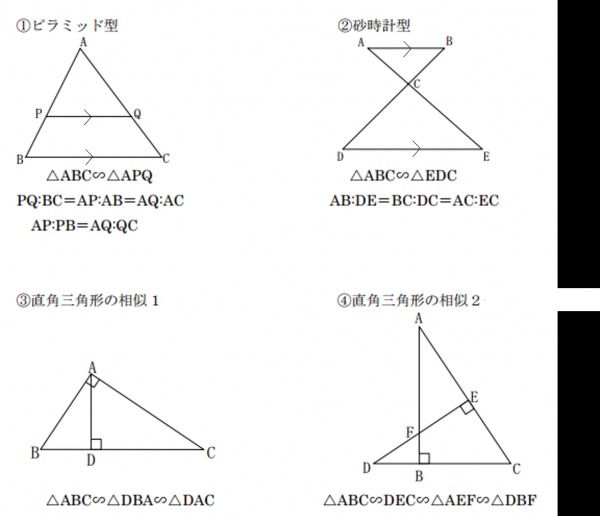
三角形の相似 合同条件 優技録

三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題

中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア
相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス

三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学

中3数学 相似の証明問題 練習編 映像授業のtry It トライイット

中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト
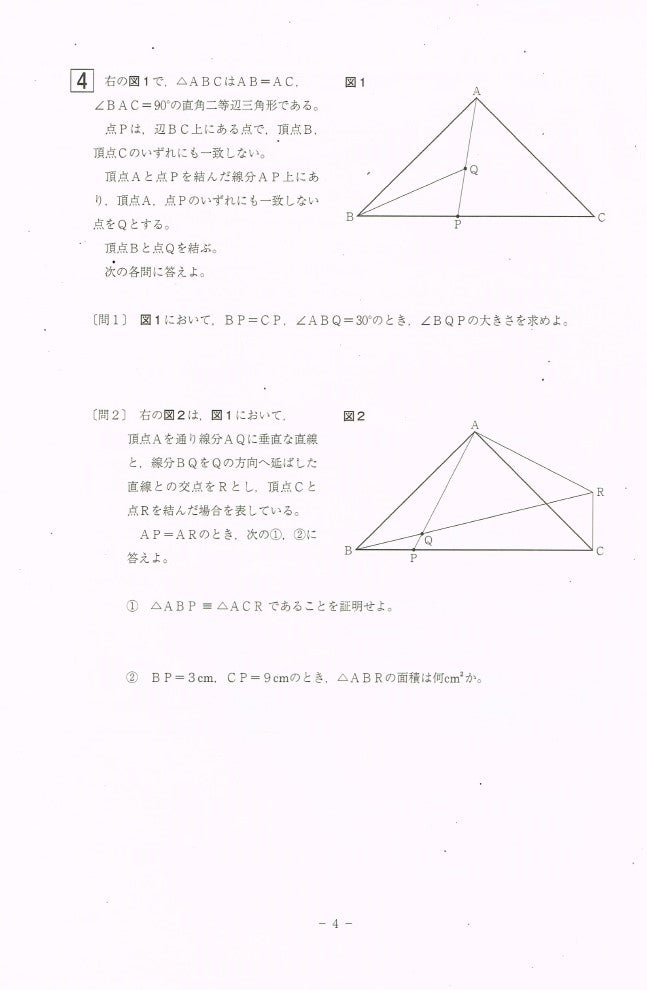
数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ

3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
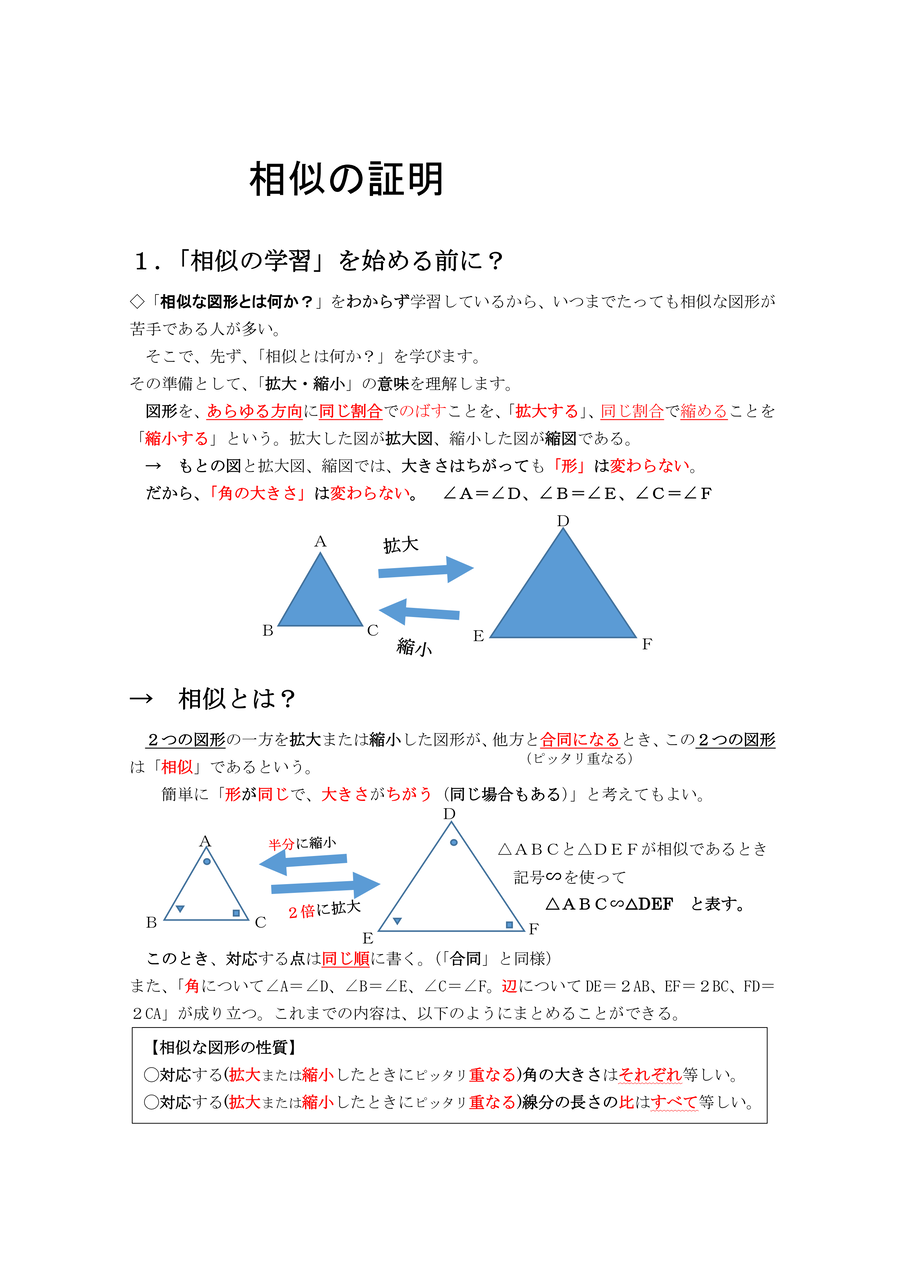
中学校数学 証明のコツ 相似

相似の証明 チーム エン
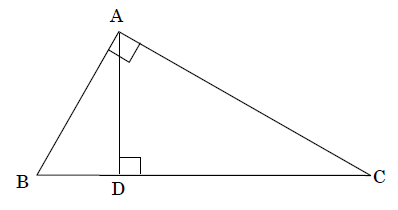
中3数学 いろいろな相似の証明の特訓練習問題 ダイスト
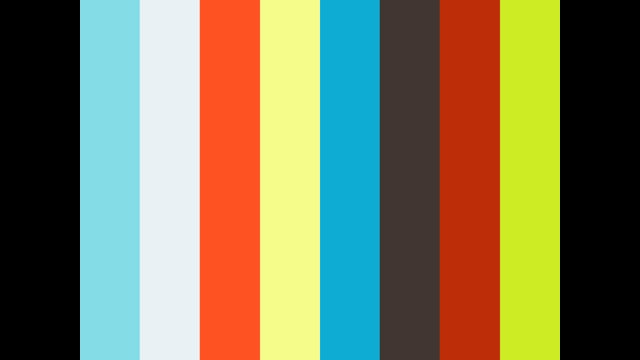
第5章6 三角形の相似 三角形の相似条件と証明 ユニバーハイスクール 高3
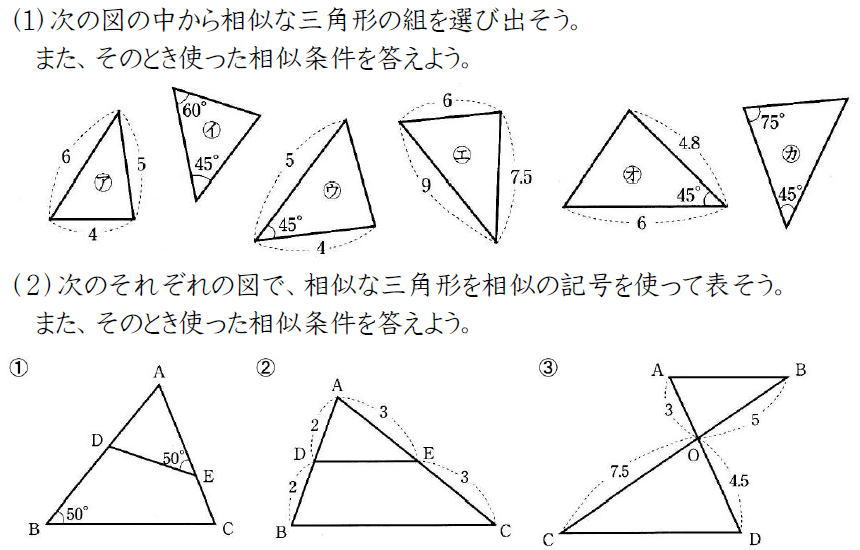
Studydoctor三角形の相似条件 中3数学 Studydoctor
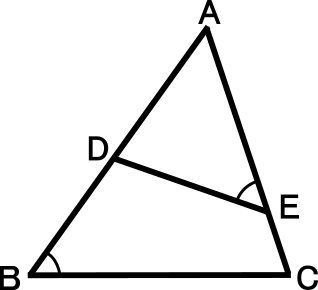
中学3年数学練習問題 三角形の相似条件と証明の問題

三角形の相似条件
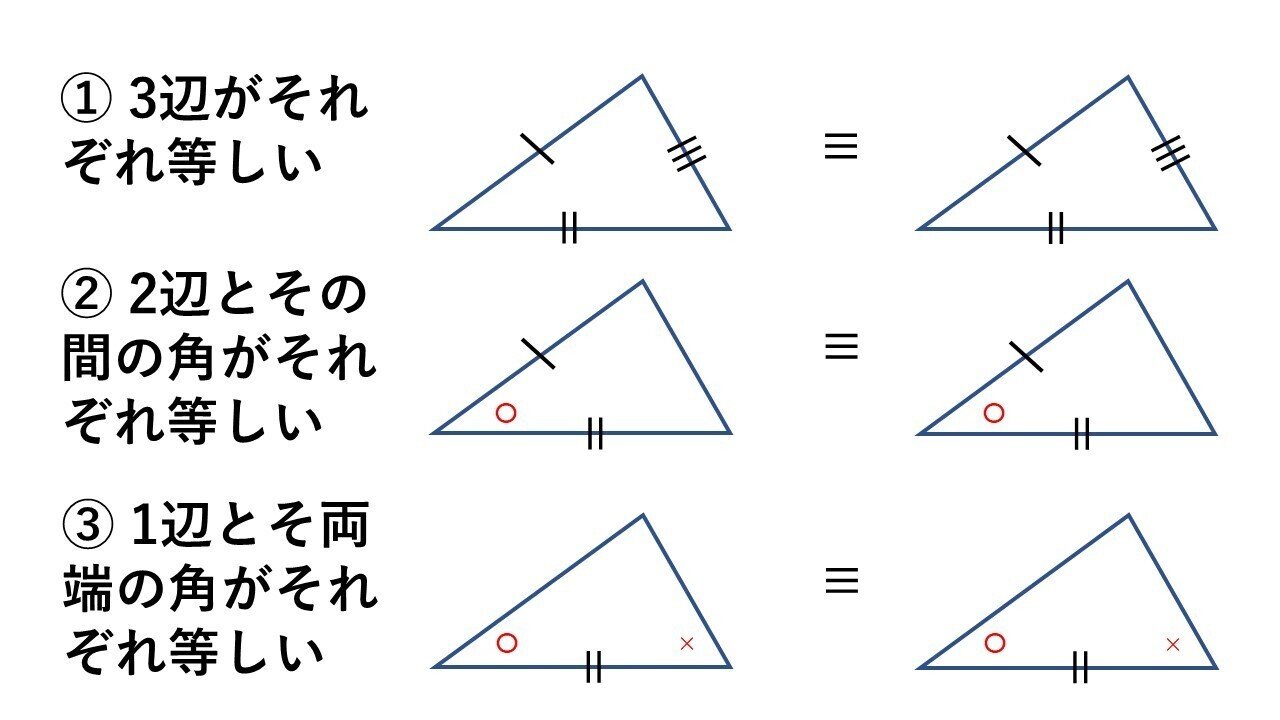
三角形の合同条件から証明へ タロウ岩井の数学 Note
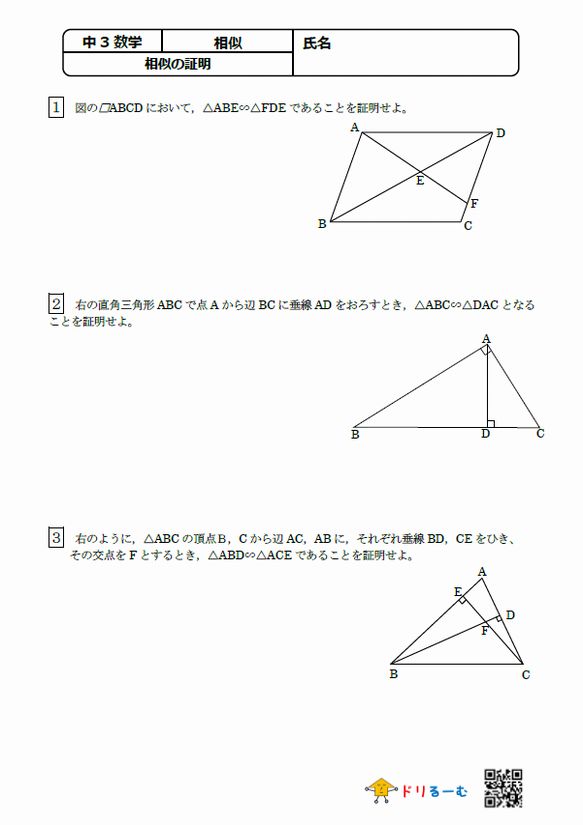
三角形の相似条件 ドリるーむ

中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
3
相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく

高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月

保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく

中3 数学 三角形の相似条件を使った証明 中学生 数学のノート Clearnote
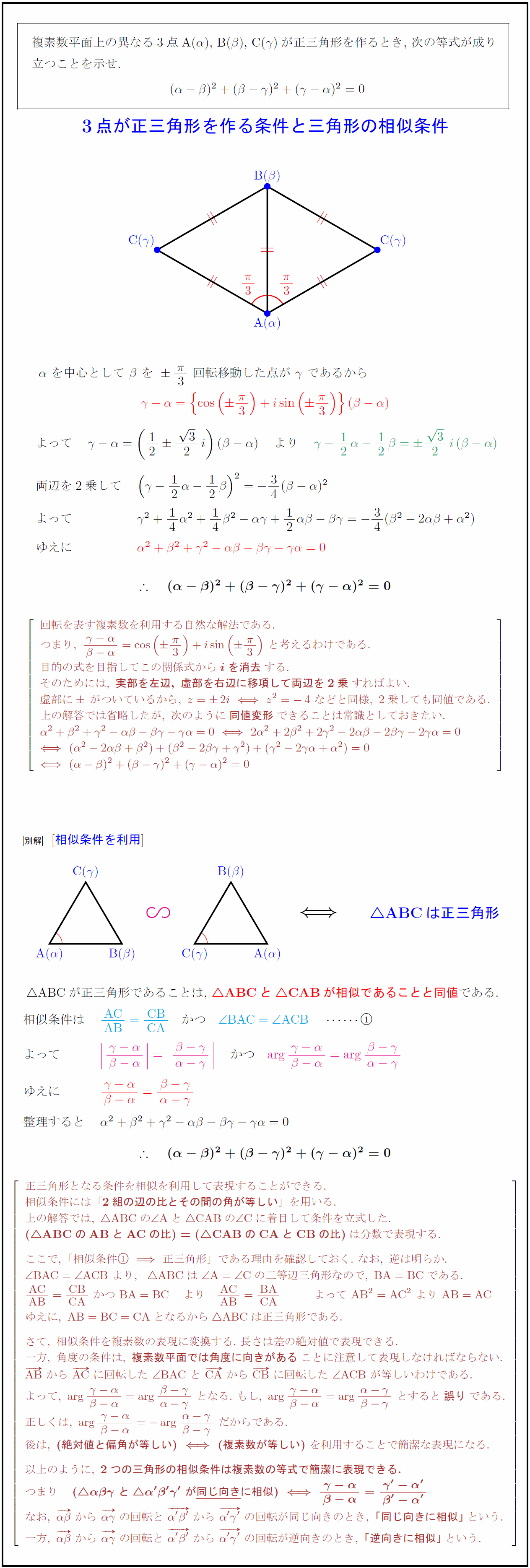
高校数学 複素数平面上で3点が正三角形を作る条件と三角形の相似条件 受験の月
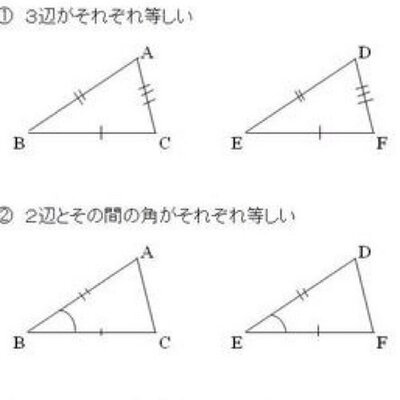
三角形の相似条件bot Triangle Bot Twitter

5章1節2 三角形の相似条件2 数学のすすめ
2

無料 中3数学 基本解説 解答プリント 327 図形の相似2 相似条件と証明
三角形の相似の証明
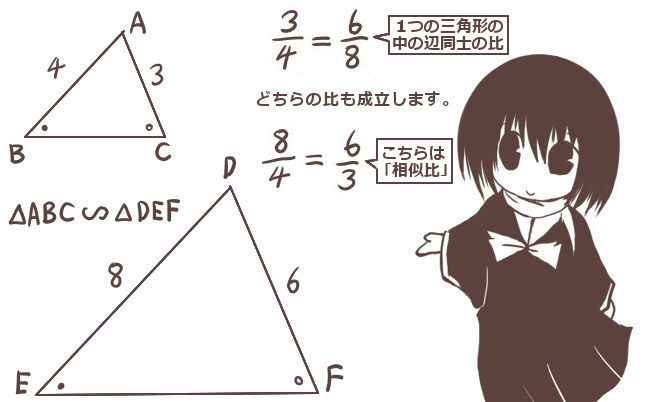
三角形の相似 理数系無料オンライン学習 Kori

三角形の合同条件と証明問題の解き方 数学fun
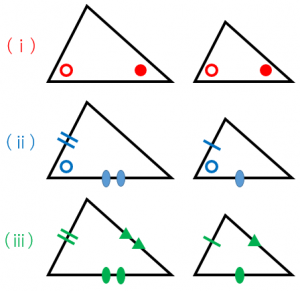
三角形の相似条件と有名な例題3問 具体例で学ぶ数学
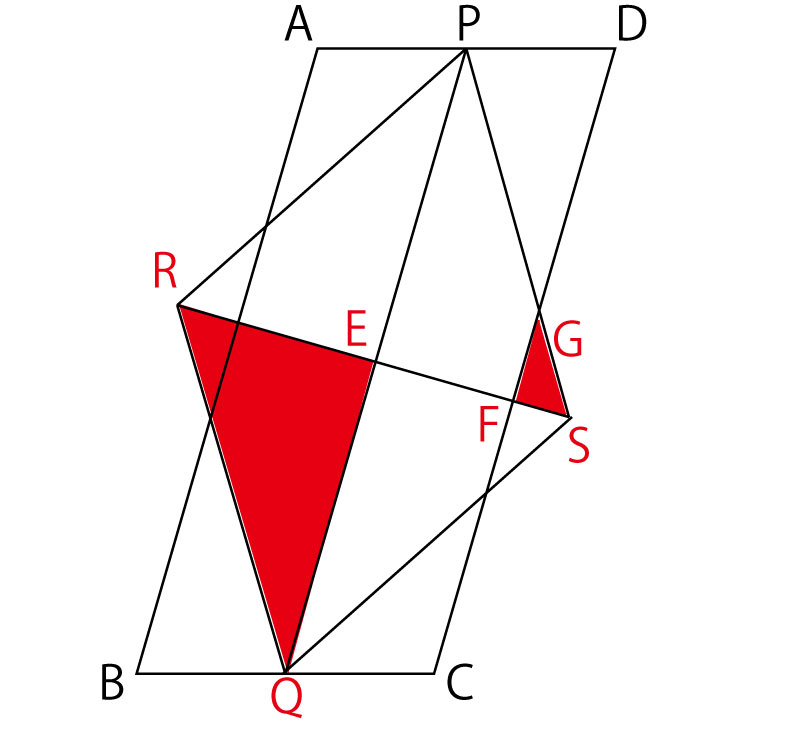
19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

Studydoctor正三角形と相似の証明 中3数学 Studydoctor

中3 相似証明問題 この下のような証明問題の場合どことどこの図形でやるか Okwave
1

無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明

三角形の相似条件
1
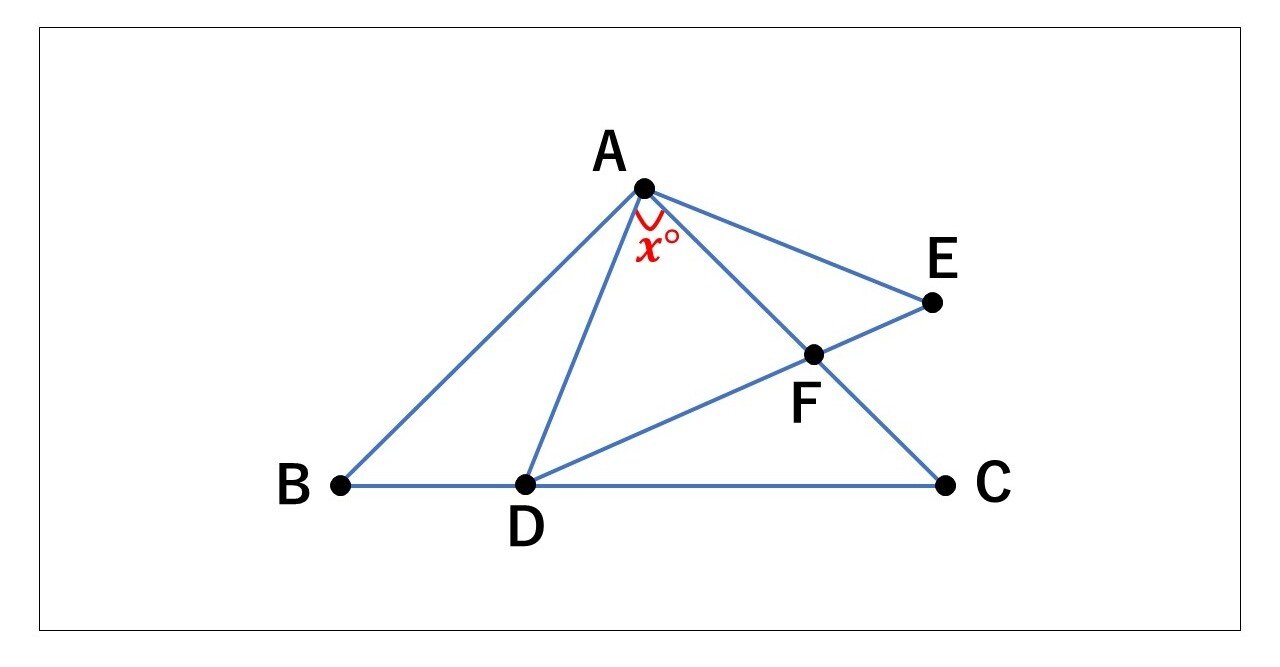
中学数学の三角形の相似の練習問題 タロウ岩井の数学 Note
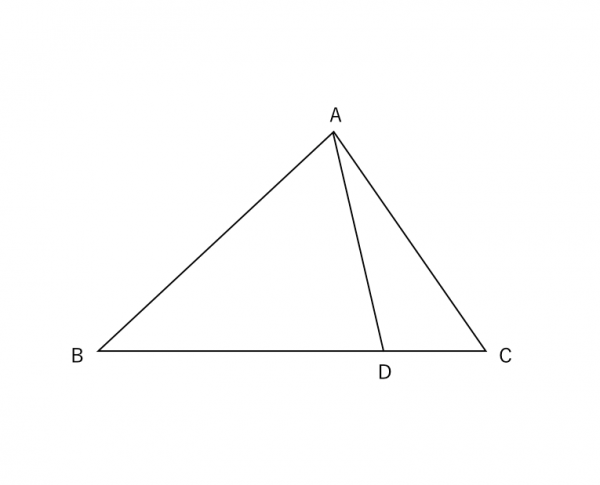
相似条件を上手く利用するポイント 苦手な数学を簡単に
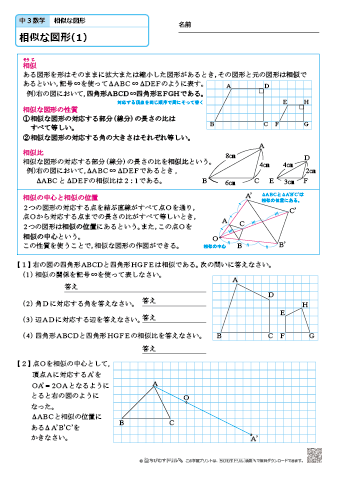
中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

世界一わかりやすい数学問題集中3 5章 図形と相似

この3問がどうしても わかりません 回答お願いいたします Clearnote

直角三角形の合同条件とその証明 数学fun

三角形の相似条件

中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座
19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学

三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
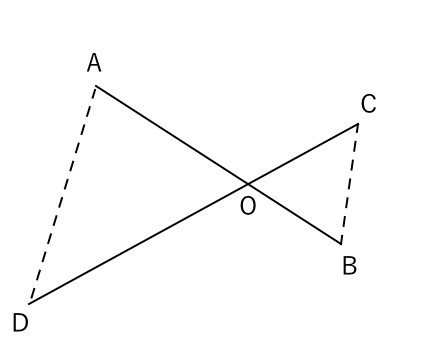
相似な図形 証明に慣れよう 苦手な数学を簡単に




