If P Then Q Q Therefore P Is An Example Of What Kind Of Common Argument
If p then q If q then r ∴ If p then r For example If Fido is a dog, then Fido is a mammal If Fido is a mammal, then Fido is warmblooded ∴ If Fido is a dog, then Fido is warmblooded We can use principles a and b from our “Modus Ponens” section (yet again!) to show that this argument is valid Try your best to invalidate it.

If p then q q therefore p is an example of what kind of common argument. Therefore, ∼ p B Valid argument If p, then q ∼ p Therefore, ∼ q B Invalid argument How to determine if an argument is valid/invalid?. A premise that depends on at least one other premise to provide joint support to a conclusion disjunctive syllogism A valid argument form Either p or q (not p or q) Not p, therefore, q hypothetical syllogism A valid argument made up of 3 conditional statements If p then q If. The invalid argument form known as affirming the consequent has this pattern if p, then q if p, then q;.
P q ~p/ q p and q represent sentences used to make statements Any argument that has the form of the disjunctive syllogism is valid Substitute any statement for p (the same statement must be used for each occurrence of p) and another statement for q The resulting argument will always be valid For example, let p = ‘It. And q is a necessary condition of the truth of if p then q but is not a necessary condition of the truth of pz q Therefore it is possible for pz q to be true when if p then q is false;. 1 If P then Q 2 P 3 Therefore, Q Valid (Modus Ponens) Notice that this argument is still valid even though (as far as we know) all the premises (and the conclusion) are, in fact, false F 1 If P then Q 2 Q 3 Therefore, P Invalid This is the same invalid form as argument B Notice that all the premises and the conclusion are in fact true.
A formal consequence must be true in all cases, however this is an incomplete definition of formal consequence, since even the argument "P is Q's brother's son, therefore P is Q's nephew" is valid in all cases, but is not a formal argument A priori property of logical consequence. False An argument of this form—If p, then q;. Disjunctive syllogism, also known as Modus Tollendo Tollens is a rule of inference of Propositional logic that states that if P or Q is true and not P is true, then Q is true What is an example of a syllogism?.
False The key to identifying an argument in context is to first identify the conclusion, then look for the premises a True b False This classic argument “The Bible says that God exists;. Q if p , then q q , ifp p , only if q p implies q p is sufcient for q q is necessary for p q follows from p c Xin He (University at Buffalo) CSE 191 Discrete Structures 15 / 37 Terminology for implication Example Proposition p. If P then Q P Therefore Q If there is nothing wrong with terminating the life of embryos, then there is nothing wrong with terminating the life of fetuses There is nothing wrong with terminating the life of embryos Therefore There is nothing wrong with terminating the life of fetuses Modus Tollens If P then Q ~ Q Therefore ~ P.
But either not q or not s;. If p then q p Therefore, q Modus Tollens A validating form of argument from propositional logic If p then q Notq Therefore, notp N Narrow Scope A term has narrow scope when it modifies the smallest part of a sentence that is grammatically possible. Either p or q If p, then r If q, then s Either r or s Example Either the evil in the universe is contrary to God's design or the evil in the universe is in accordance with God's design If the evil in the universe is contrary to God's design, then God is not all powerful.
Let “p”=”(A ˅ B)” and let “q”=”(A B)” The argument in symbolic form is this p Ɔ q q _____ p Since this only occurs in more complicated arguments, however, you can ignore this sort of exception in this course 3 Common Valid Dilemma Forms There are two more valid argument forms These. Therefore, God exists” is an example of begging the question a True. Let p and q be statement variables which apply to the following definitions The conditional of q by p is "If p then q " or " p implies q " and is denoted by p q It is false when p is true and q is false;.
Therefore they are true conjointly Addition p ∴ (p∨q) p is true;. An example of a syllogism is "All mammals are animals All elephants are mammals Therefore, all elephants are animals". CMSC 3 Section 01 Homework1 Solution CMSC 3 Section 01 Homework1 Solution 1 Exercise Set 11 Problem 15 Write truth table for the statement forms (5 points) ~(p ^ q) V (p V q).
And if p then r;. Therefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;. Explanation The form of a modus ponens argument resembles a syllogism, with two premises and a conclusion If P, then Q P Therefore, Q The first premise is a conditional ("if–then") claim, namely that P implies QThe second premise is an assertion that P, the antecedent of the conditional claim, is the case From these two premises it can be logically concluded that Q, the.
If P, then Q Q Therefore, P This is an invalid argument form Consider this argument, which affirms the consequent If Jones is years old, then Jones is younger than 50 years old Jones is younger than 50 years old Therefore, Jones is years old Clearly, this argument is a bad one Jones could be any age younger than 50. If P then Q(P is the antecedentand Q is theconsequence) If the antecedent is true then the consequent must be true It is not claiming anything about the consequent if the antecedent is false Logical Implication– The consequent follows logically from the antecedent (ie All men are mortal and Socrates is a man, then Socrates is mortal). Famous If P, Then Q Logical Argument Example Premise #1 If (P) this rock hits that window, then (Q) that window will break Thus, in the precise specifications of the P/Conditions/Causes and therefore the causes of the Q/Consequence(s)/Effect(s) of an If P, Then Q logical argument we find the basis for true knowledge, the accurate.
Mathematics, a variety of terminology is used to express p !. 1statement variables p and q are substituted for component statements “Dogs bark” and “Cats meow,” respectively 2truth table shows that for each combination of truth values for p and q, p ∧ q is true when, and only when, q ∧ p is true In such a case, statement forms are called logically equivalent, and we say that (1) and (2) are. Let’s do one that is slightly longer Here’s a truth table for P &(Q∨R) P & ( Q ∨ R) We’ll go ahead and write the formula and sentence letters, and draw the lines P Q R P & (Q ∨ R) P Q R P & ( Q ∨ R) It gets more difficult to fill in the combinations of truth.
Otherwise it is true The contrapositive of a conditional statement of the form "If p then q ". Therefore if p is true. And if r then s;.
Note the statements p > q and q > p are not equivalent q > p is called the converse of p > q and the converse of an implication cannot be used to prove that the implication is true A converse may or may not be true but its truth value has no relation to. 7 Modus tollens premises, conclusion Common form (modus tollens) If p, then q (premise) Not q (premise) Therefore not p (conclusion) A premise is a statement presumedtrue for purposes of. Premise 1 If P, then Q Premise 2 Q Conclusion P Appealing to Extremes taking an assertion to an extreme, even though the arguer may never take it to that extreme Example "Avid health advocates blow out their knees by their 50s by running marathons Therefore, don't prioritize regular exercise" But not all avid health.
The first step in investigating possible implicit premises is to a Search for a credible premise that would make the argument as strong as possible b Rewrite the argument c Search for a credible premise that would make the argument valid d Make a bad argument good Modus ponens has this argument pattern. Therefore either not p or not r Simplišcation (p∧q) ∴ p p and q are true;. Philosophy 244/244W/444 Philosophy of Mind Fall 06 Arguments An argument is a sequence of declarative sentences The last sentence in the sequence is the conclusion of the argument The sentences preceding the conclusion are the premises of the argument Some Sample Arguments.
All that it is, is a claim that if P is true, then Q is also true — without making any more claims than this An alternative way of considering P ⊃ Q is as a "constraint" that. Therefore, not q Sentence A valid argument form If p, then q Not q Therefore, not p syllogism Vocab A deductive argument made up of three statements two premises and a conclusion truthpreserving. If P, then Q P Therefore, Q Premise Premise Conclusion If we fill in values for P and Q that make the premises of the argument true, then it is impossible for the conclusion to be false That’s what makes an argument valid.
The part of a conditional statement (If p, then q) introduced by the word then Deductive Argument An argument intended to provide logically conclusive support for its conclusion described as valid or invalid Denying the Antecedent An invalid argument form If p, then q Not p Therefore, not q Denying the Consequent (Modus Tollens). An argument with this form—"If p, then q If q, then r Therefore, if p, then r"—is known as Question 6 options a) Hypothetical syllogism b) Modus tollens. Therefore p is true Conjunction p,q ∴ (p∧q) p and q are true separately;.
Therefore, not q —is called modus tollens a True b False This argument form known as modus tollens is valid a True. The Bible is true because God wrote it;. For example, consider this which includes a fallacy of affirming the consequent "If it is raining the ground will be wet The ground is wet If p then q q Therefore p This kind if argument is also called a CON This is common to get someone to fall for scheme to get money.
Section24 Logical Arguments Definition 241 An argument is a sequence of statements ( premises) that ends with a conclusion A valid argument is one where the conclusion follows from the truth of the premises For the sequence of premises p1,p2,,pn p 1, p 2, , p n and conclusion q, q, an argument is valid if. The first step in determining whether an argument isdeductive or inductive is to find the argument's conclusion and thenits premises. Invalid argument form, if p then q, q therefore p denying the antecedent invalid argument form, if p then q, not p therefore not q suppressed evidence withholding evidence that would be damaging to the conclusion (withholding the evidence that an eyewitness was under the influence when witnessing a crime) straw man.
Method 1 Construct a truth table 1 Identify the premises and conclusion 2 Construct a truth table for premises and conclusion 3 A row of the truth table in which all the premises are true is called. Therefore, the argument must be valid 5 Valid We can test for validity by substituting statement variables into the argument If we do the substitution, we get If p, then q Not q Therefore, not p Upon inspection, we find that this is one of the common patterns of valid inference discussed above—modus tollens. How to think about "P ⊃ Q" in plain EnglishIn propositional logic, P ⊃ Q is what is called a material implicationIt doesn't mean that P and Q mean the same thing (they might not have the same truth value);.
Anselm’s argument is an a priori argument;. A dilemma is a form of reasoning that presents a choice between two alternatives Here is an example “If P then Q And if R then also Q But either P or R So in any event, Q” Dilemmas are perfectly respectable forms of argument In an argument of this sort, P and R are called “the horns” of the dilemma. In propositional logic, modus tollens, also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference Modus tollens takes the form of "If P, then Q Not Q Therefore, not P" It is an application of the general truth that if a statement is true, then so is its contrapositive The form shows that inference from P implies Q to the negation.
If p then q;. That is, it is an argument that is independent of experience and based solely on concepts and logical relations, like a mathematical proof The form of the argument is that of a reductio ad absurdum argument Such an argument works like this Suppose P If P, then Q. This is just the truth table for \(P \imp Q\text{,}\) but what matters here is that all the lines in the deduction rule have their own column in the truth table Remember that an argument is valid provided the conclusion must be true given that the premises are true The premises in this case are \(P \imp Q\) and \(P\text{}\).
And so if and v are not interderivable (p 114) Faris's defence of the horseshoe against the Connection Argument. Example 15 As we noted above, the argument p → q q → r p∨q → r is a perfectly valid argument Let p =“I sleep a lot”, q =“I don’t do any homework” and r =“I will do well in this class” Then this translates to “If I sleep a lot, then I don’t do any homework If I don’t do any.

Discrete Mathematics With Applications 4th Edition Susanna Solutions

Logical Arguments
Degruyter Com
If P Then Q Q Therefore P Is An Example Of What Kind Of Common Argument のギャラリー

Solved Qucrtion 3 Points 3 Points Determine Whether The Following Argument Forms Valid Ifp Then Q If Q Then P Not P And Q Not P Or Not Q Question 2
6 Conditional Derivations A Concise Introduction To Logic

Formal Logic The Propositional Calculus Britannica
1

Formal Logic The Propositional Calculus Britannica

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero

Chapter 3

Ch 3 Making Sense Of Arguments Flashcards Quizlet

Logical Arguments
Jstor Org

Cse15 Discrete Mathematics 01 30 17 Ppt Download
Wm Edu

Solved Which Of The Following Symbolizes A Modus Tollens Chegg Com
Portail Telecom Bretagne Eu
Stetson Edu

1 Cpan 110 Week 9 Module 1 Creating Valid Arguments Diagramming Arguments Ppt Download

Cs 103 Discrete Structures Ppt Download

Adverbial S As Last Resort Springerlink
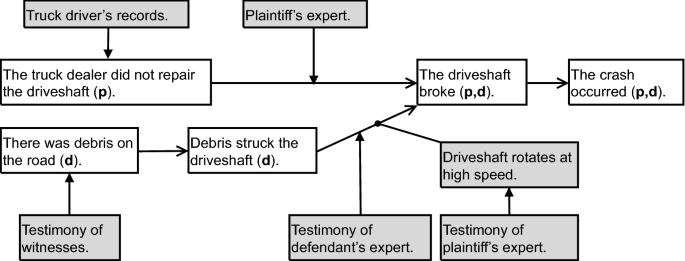
In Memoriam Douglas N Walton The Influence Of Doug Walton On Ai And Law Springerlink

Intro Logic Chaps 6 And 7

13 Logic And Reasoning Ideas Logic Inductive Reasoning Philosophy

Solved Question 2 40 Marks A Use Truth Tables To Chegg Com
Degruyter Com

Truth Table To Determine If An Argument Is Valid Youtube
Jstor Org
4 Proofs A Concise Introduction To Logic

Ppt Verifying Arguments Powerpoint Presentation Free Download Id

Valid Forms Ck 12 Foundation
Degruyter Com

Intro Logic Chaps 6 And 7
6 Conditional Derivations A Concise Introduction To Logic

Ii If P Then Q Q Therefore P Can You Name This Form The Above Type Of Argument Course Hero
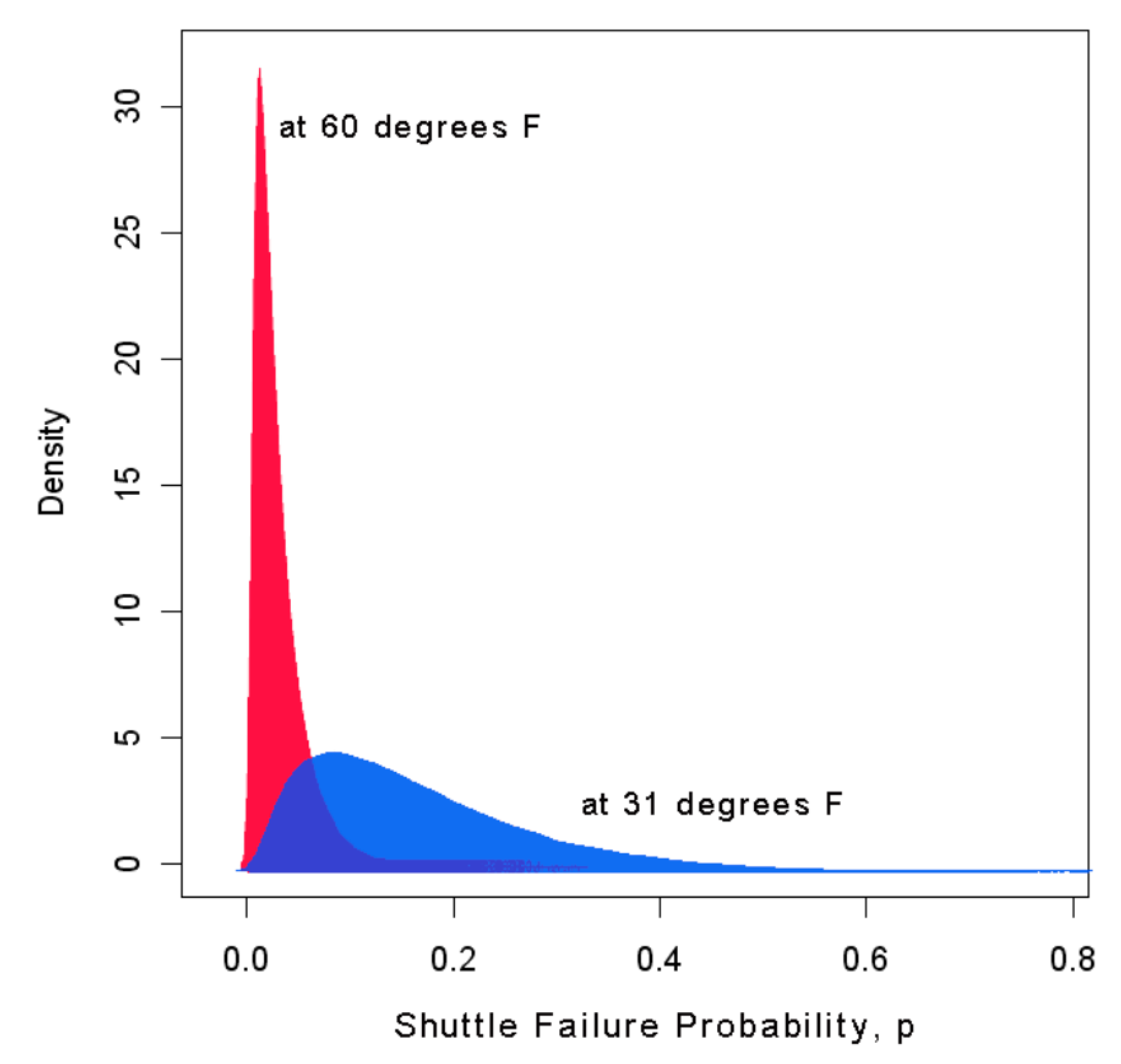
Sustainability Free Full Text Risk Assessment Models To Improve Environmental Safety In The Field Of The Economy And Organization Of Construction A Case Study Of Russia Html
Www3 Cs Stonybrook Edu
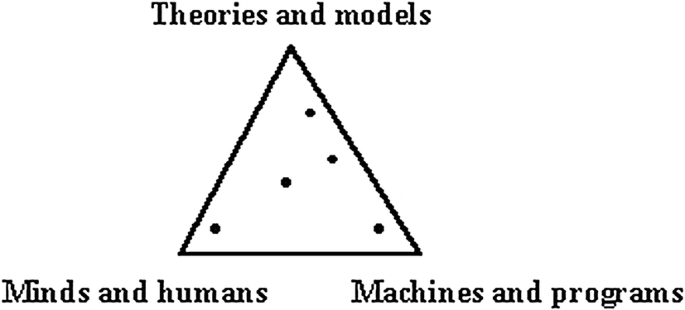
In Memoriam Douglas N Walton The Influence Of Doug Walton On Ai And Law Springerlink
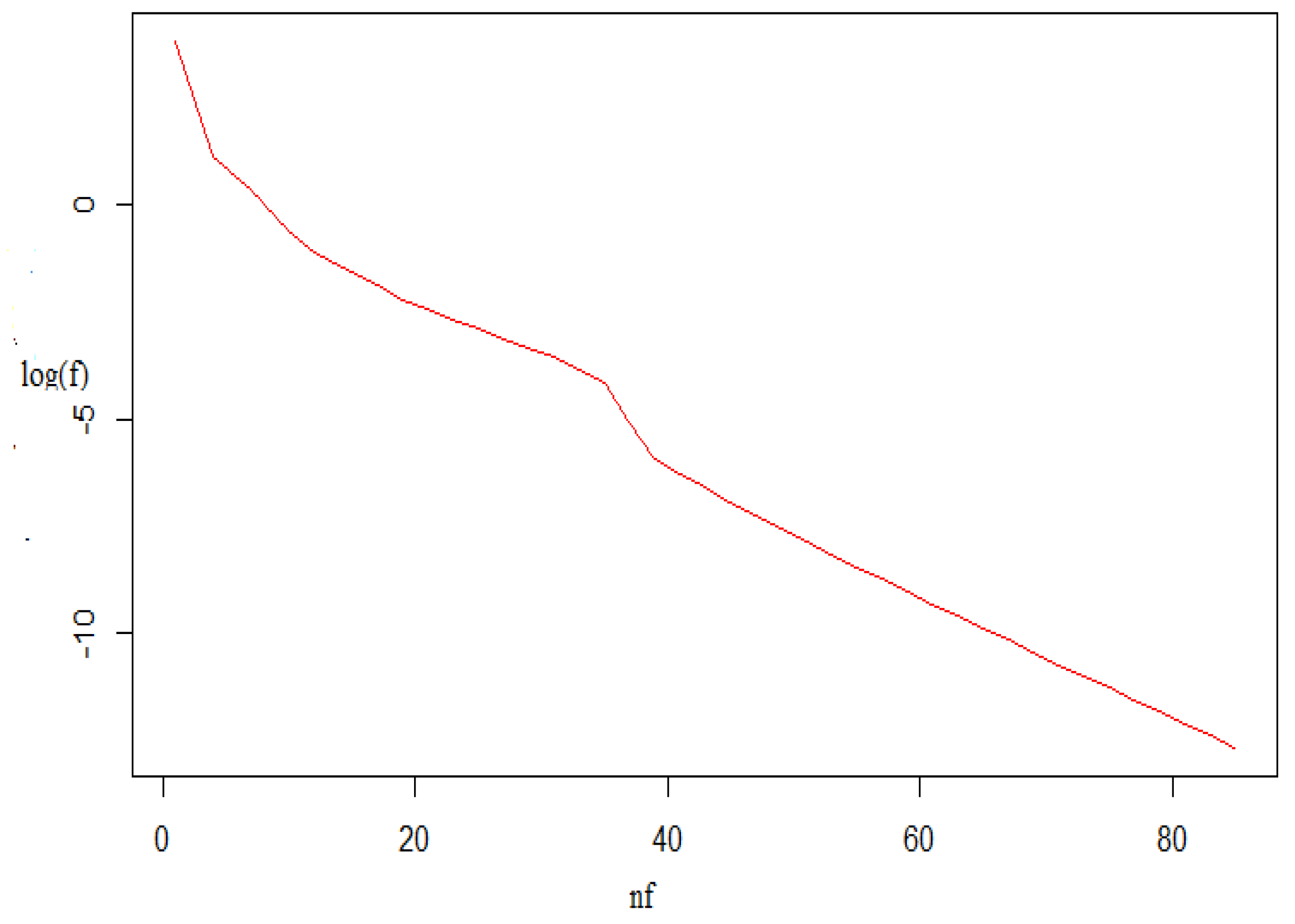
Fractal Fract Free Full Text A Q Gradient Descent Algorithm With Quasi Fejer Convergence For Unconstrained Optimization Problems Html

Solved Consider The Argument Form P Rightarrow Tilde Q Q Chegg Com

Questions With Answers In Pure Mathematics Science Topic

Philosophy 103 Linguistics 103 Yet Still Even Further

Logic Propositions N N A Proposition Is A
Degruyter Com

Truth Table To Determine If An Argument Is Valid Youtube

Argument Quality In Real World Argumentation Trends In Cognitive Sciences

Logical Fallacies Logical Fallacies Are Statements That May
A Secure And Efficient Certificateless Content Extraction Signature With Privacy Protection

Evaluating Philosophical Claims And Theories Ppt Video Online Download
Royalsocietypublishing Org

Solved 2 Besides And 0r And Not There Is One More Basic Logical Operator It S The Conditional If Then Form In Mathematical Logic The Statement If P Then Q Is False Only When

Argument Quality In Real World Argumentation Trends In Cognitive Sciences

Ii If P Then Q Q Therefore P Can You Name This Form The Above Type Of Argument Course Hero

Solved Question 2 5 5 10marks A Use Valid Argument Forms Chegg Com

Solved Which Of The Following Symbolizes A Modus Tollens Chegg Com

Philosophy 103 Linguistics 103 Yet Still Even Further

Rules Of Inference Detailed W Step By Step 7 Examples

End Of Chapter 3 Critical Thinking

Argument Quality In Real World Argumentation Trends In Cognitive Sciences

Chapter 22 Common Propositional Argument Forms Introductory Remarks P 2 This Chapter Introduces Some Of The Most Commonly Used Deductive Argument Ppt Download
1

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero

Logical Arguments Modus Ponens Modus Tollens Youtube

Chapter 3
Condor Depaul Edu

A Dialogical Route To Logical Pluralism Springerlink
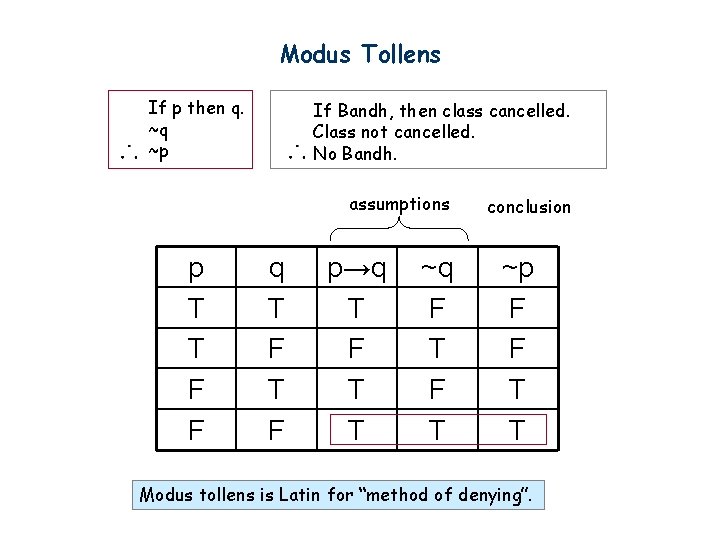
Propositional Logic Conditional Statement If P Then Q
Unsworks Unsw Edu Au

Philosophy Logic And Logical Arguments Ppt Video Online Download

Cs 103 Discrete Structures Lecture 07b Ppt Download
Affirming The Consequent

Validity Soundness And Valid Patterns Valid Patterns Saylor Academy
Degruyter Com
Degruyter Com

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero
Jstor Org

Logic Propositions N N A Proposition Is A

Exercises Questions And Activities Pages 1 19 Flip Pdf Download Fliphtml5

Solved Which Of The Following Symbolizes A Modus Tollens Chegg Com
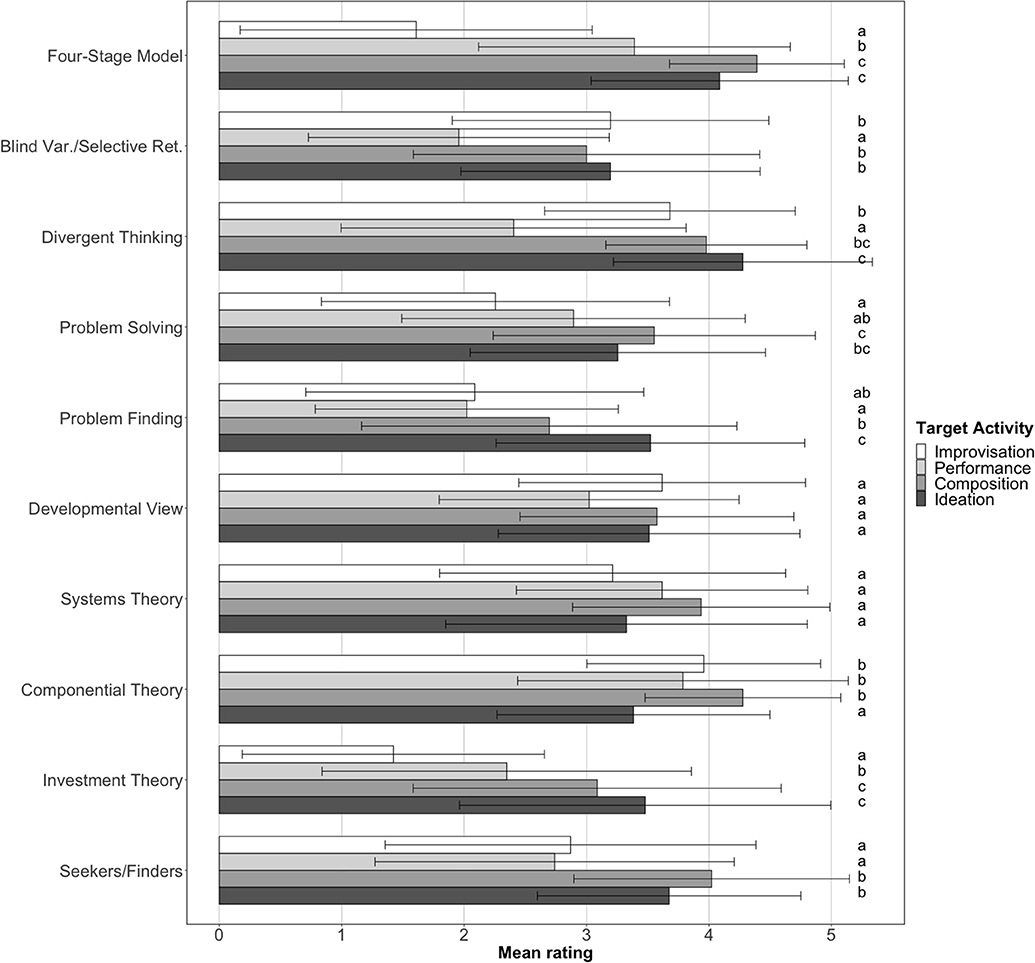
Frontiers Theories Of Creativity In Music Students Theory Appraisal And Argumentation Psychology

Ppt Deductive Validity Powerpoint Presentation Free Download Id
Philarchive Org

Reasoning And Argumentation Oxford Research Encyclopedia Of Psychology

Argument Quality In Real World Argumentation Trends In Cognitive Sciences

In Praise Of Rationality The New York Times

Philosophy 103 Linguistics 103 Yet Still Even Further
Jstor Org

1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download
Frontiers English Speakers Implicit Gender Concepts Influence Their Processing Of French Grammatical Gender Evidence For Semantically Mediated Cross Linguistic Influence Psychology
Jstor Org

Philosophy 103 Linguistics 103 Yet Still Even Further

1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download
Scielo Br
6 Conditional Derivations A Concise Introduction To Logic

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download

Critical Thinking Study Guide Study Guide Terms Antecedent The First Factor Upon Which The Studocu

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download
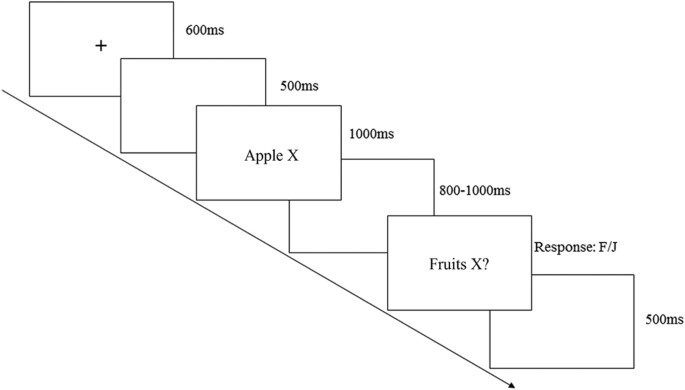
How Types Of Premises Modulate The Typicality Effect In Category Based Induction Diverging Evidence From The P2 P3 And Lpc Effects Scientific Reports

Ppt Logic Powerpoint Presentation Free Download Id

Intro Logic Chaps 6 And 7

1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download
Sqa Org Uk
Siue Edu




