Yx2 Cut
2 nˇ b 2 121 Cuto frequency For a TM @2F @x 2 FK @2G @y FG @2K @z k2FGK= 0 We divide by FGK 1 F @2F @x 2 1 G @ 2G @y k2 = 1 K @K @z2 The left hand side is independent of zand the right hand side is independent of x;y The only way that this can happen is if both sides are constant We call this.
Yx2 cut. x = √1 8 y or x = √1 8y−1 for the curve x = y2, the derivative with respect to y is 2y for the curve x = √1 8 y−1, the derivative with respect to y is −√1 8 y−2 the point at which the two curves meet is when y2 = √1 8 y y2 = √1 8 y y3 = √1 8 y = √ 1 2 since x = y2, x = 1 2. Find the area of the finite part of the paraboloid $ y = x^2 z^2 $ cut off by the plane $ y = 25 $ Hint Project the surface onto the $ xz $plane Answer $\frac{\pi}{6} \cdot(101 \cdot \sqrt{101}1)$ View Answer Related Courses Calculus 3 Calculus Early Transcendentals Chapter 15 Multiple Integrals. The circle \(x^2y^2 4x7y12=0\) cuts an intercept on yaxis of length This question was previously asked in BSF RO Official Paper (Conducted on 22Sep19).
{x∈Q x>0 and x2 0 and x2 ≥2} In this example neither Anor Bhas an extremal element The first exercise below shows that, with regard to extremal elements, every cut is. Q If the line `y = mx 2` cuts the parabola `2y = x^2` at points `(x_1,y_1)` and `(x_2,y_2)` where `(x_1 x_2)` then the value of `m` for which `∫_(x_1)^(x_2) (mx2−x^2/2) dx` is. If the curves ay x^2 = 7 and y = x^3 cut each other orthogonally at a point, find a asked in Limit, continuity and differentiability by SumanMandal ( 546k points) the tangent and normal.
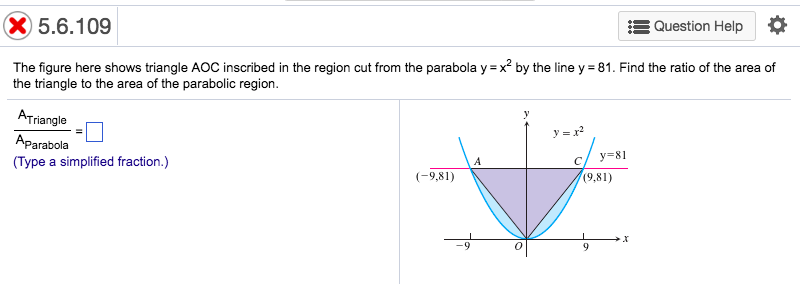
Find the area of the finite part of the paraboloid {eq}y = x^2 z^2 {/eq} cut off by the plane {eq}y = 81 {/eq} (Hint Project the surface onto the xzplane). If the curve ay x 2 = 7 and x 3 = y, cut orthogonally at (1, 1), then the value of a is (A)1 (B) 0 (C) –6 (D) 6 Next Question 11→ Chapter 6 Class 12 Application of Derivatives (Term 1) Serial order wise;. Consider the equation y=x3−x22x y = x 3 − x 2 2 x Whenever the graph passes through the X axis, the Y coordinate of the point of intersection would be 0 0 ⇒ ⇒ The graph will cut the X axis whenever x3−x22x=0 x 3 − x 2 2 x = 0 x3−x22x=0⇒x (x2−x2)=0 x 3 − x.
Find the area of the smaller part of the circle `x^2y^2=a^2` cut off by the line `x=a/(sqrt(2))` Find the area of the smaller part of the circle `x^2y^2=a^2` cut off by the line `x=a/(sqrt(2))` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous. Solution for At what acute angle does the curve y = 1 – 05 x2 cut the xaxis?. Answer Tangent at vertex is y axis Latus rectum is at x=a Curved surface generated = ∫2π(ax) ds where ds/dx=√(1dy/dx)^2 =∫2π(ax)√(14a^2/y^2)dx = 2π∫(ax)√(1a/x)dx for range x=0 to a Further solution needs to be worked out.
Find the slope of the tangent to a parabola y = x 2 at a point on the curve where x = ½ A 0 93 Find the acute angle that the curve y = 1 – 3x 2 cut the xaxis. Q6 Two parallel lines L 1 and L 2 are cut by a transversal T Use the figure to find how are y = (2 x) From step 4 Step 6 y = 2(15) = 30 Step 7 So, x = 15 and y = 30 Correct Answer is x = 15 and y = 30 Q13 The lines l and m are parallel Find the values of x and y in the figure shown A. 1 x 2 t sx x 1 x 2 • There is 11 correspondence every edge in network and every term in f • Let us denote source by and sink by s t0 1 • An edge that goes from to is denoted by 2 x x 1 x 2 1 x 2 Network model for submodular QPBF.
SOLUTION 1 Let variables x and y represent two nonnegative numbers The sum of the two numbers is given to be 9 = x y, so that y = 9 x We wish to MAXIMIZE the PRODUCT P = x y 2 However, before we differentiate the righthand side, we will write it as a function of x only Substitute for y getting P = x y 2 = x ( 9x) 2 Now differentiate this equation using the product. Show Solution Okay, since we are looking for the portion of the plane that lies in front of the y z y z plane we are going to need to write the equation of the surface in the form x = g ( y, z) x = g ( y, z) This is easy enough to do x = 1 − y − z x = 1 − y − z Next, we need to determine just what D D is. The coordinates are, (x,y) = ( a2 b2a2(b2 c2) , a2 b2b2(a2 − c2) ) Since the curves intersect at right angles, then their slopes at that point will be perpendicular That is, the product of slopes will be −1 Differentiating both the equations,.
NCERT Exemplar MCQs Question 1 Important Question 2. Select three that apply A Each pair of vertical angles is congruent B Each pair of corresponding angles is congruent C Each pair of supplementary angles is congruent D. The coordinates of points at each of which the tangents to the curve $y=x^33x^27x6$ cut off on the negative semi axis $OX$ a line segment half that on the positive.
2) x = 4 8 Two parallel lines are cut by a transversal Which statements are true for all such cases?. The parabolas x^2 = 5 4y and y = x^2 cut at the point (1, 1) at an angle Question The parabolas x 2=5−4y and y=x 2 cut at the point (1,1) at an angle A 2π B 4π C 3π D none of these Medium Solution Verified by Toppr Correct option is A 2π For x 2=5−4y Slope dxdy = −42x =− 21 =m 1 And for y=x 2 Slope dxdy =2x=2=m 2 Therefore, tan(θ)= ∣∣∣∣∣∣ 1m 1. Lines are said to intersect each other if they cut each other at a point By Euclid's lemma two lines can have at most 1 1 1 point of intersection Find the intersection of the lines y = 3 x − 3 y = 3x 3 y = 3 x − 3 and y = 23 x 4 y = 23x 4 y = 2 3 x 4.
Cut is an HM move that you can find in every Pokémon game It allows you to cut down trees that are in your way, allowing you to get to new areas and get items This article will explain how you can get it in Pokémon X and Y Get to the. Answer Volume V of the solid generated by revolving the area cut off by latus rectum (x = a) of the parabola y^2 = 4ax, about its axis, which is x axis, is. The tangent and the normal drawn to the curve y = x^2 – x 4 at P(1, 4) cut the X – axis at A and B respectively If the length of the subtangent drawn to the curve at P is equal to the length of the subnormal then the area of the triangle PAB is sq units is.
Find the area of the surface G cut from the hemisphere x2y2z2=42, z≥0, by the plane z=1 and z=3 by setting up an integral Method 1 Cylindrical Coordinates Set up the Integral 2 42−r2 rdrdθ r=7 ∫15 θ=0 ∫2π 2 42−r2 rdrdθ r=7 ∫15 θ0 ∫2π (5 pts) (5 pts) (5 pts) The surface area of the hemisphere between z=1 and z=3 is 1(f x) 2f (y) 2 S ∫= −x. INTEGRAL LINKS Basic Integral Problems https//youtube/gZKoyR6ZcgIntegration by parts ∫ log x/x^2 dx https//youtube/SVGDrup8EyMINTEGRATE ∫ 1/(√9x. Of a curved wedge cut out from a cylinder (x − 2)2 y2 = 4 by the planes z = 0 and z = −y Solution First sketch the integration region I (x − 2)2 y2 = 4 is a circle in the xyplane, since x2 y2 = 4x ⇔ r2 = 4r cos(θ) r = 4cos(θ) I Since 0 6 z 6 −y, the integration region is on the y 6 0 part of the z = 0 plane y z = y 2 4 z x (x 2) y = 42 2.
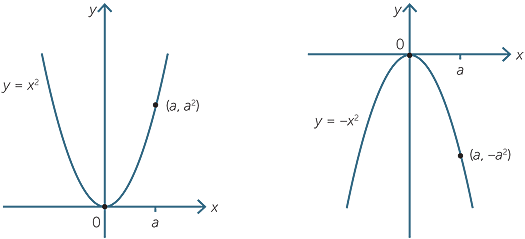
The Parabola y = x 2 Students will be familiar from earlier years with the graph of the function y = x 2 which they obtained by making up a table of values and plotting points This graph is called a parabolaThe path of a ball tossed under gravity at an angle to horizontal (roughly). Rant bounded by the lines y = x, y = 2x,x = l, x = 2 Square = l/(xy) over the square I s x 2, Triangle f(x, y) = x2 over the triangular region with ver tices (O, O), (l, 0), and (0, l) Rectangle f(x,y) = y cosxy over the rectangle 0 x 7, Triangle flu, v) = v over the triangular region cut. The f (x) curve is above the xaxis from x=0 to the point where 2x = x^2, which is x = 2 The area is INTEGRAL (2x x^2) dx = x^2 x^3/3 @x=2 0 to 2 = 4/3 That agrees with what you obtained You want the area under y = mx to be 2/3.
The general solution is \frac {\tanh \left (\frac {x} {2}i c\right)} {2 x} To get it change the variable z (x)=x y (x) after that it is standard The general solution is − 2xtanh(2x −ic) To get it change the variable z(x) = xy(x) after that it is standard About Pathconnected. First, we need to recall just how spherical coordinates are defined The following sketch shows the relationship between the Cartesian and spherical coordinate systems Here are the conversion formulas for spherical coordinates x = ρsinφcosθ y = ρsinφsinθ z = ρcosφ x2y2z2 = ρ2 x = ρ sin . A 3454° b 4464° c 5474° d 6484°.
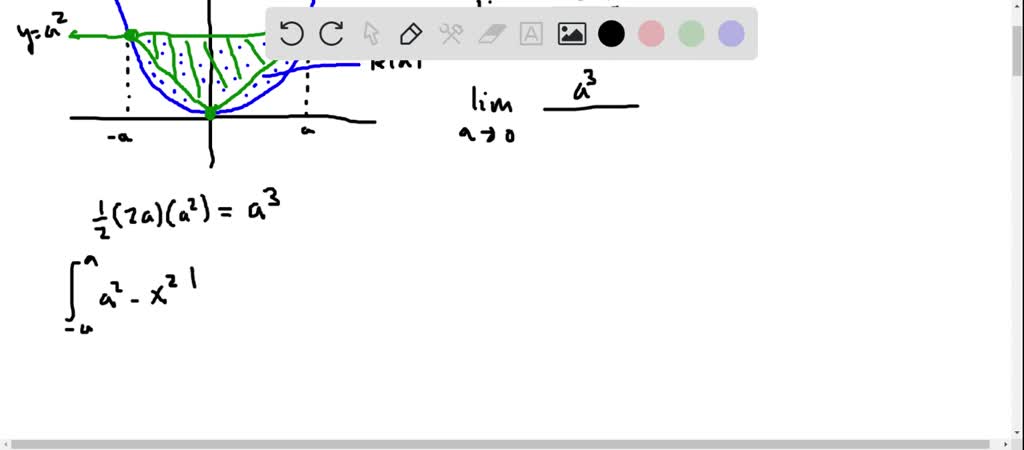
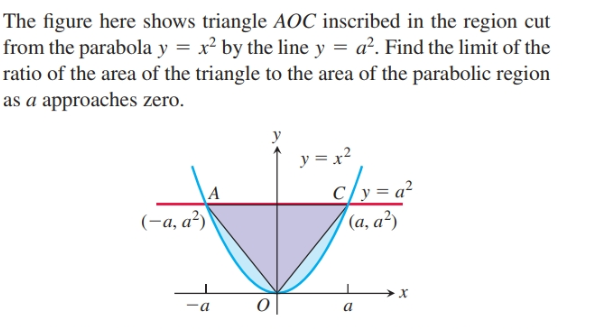
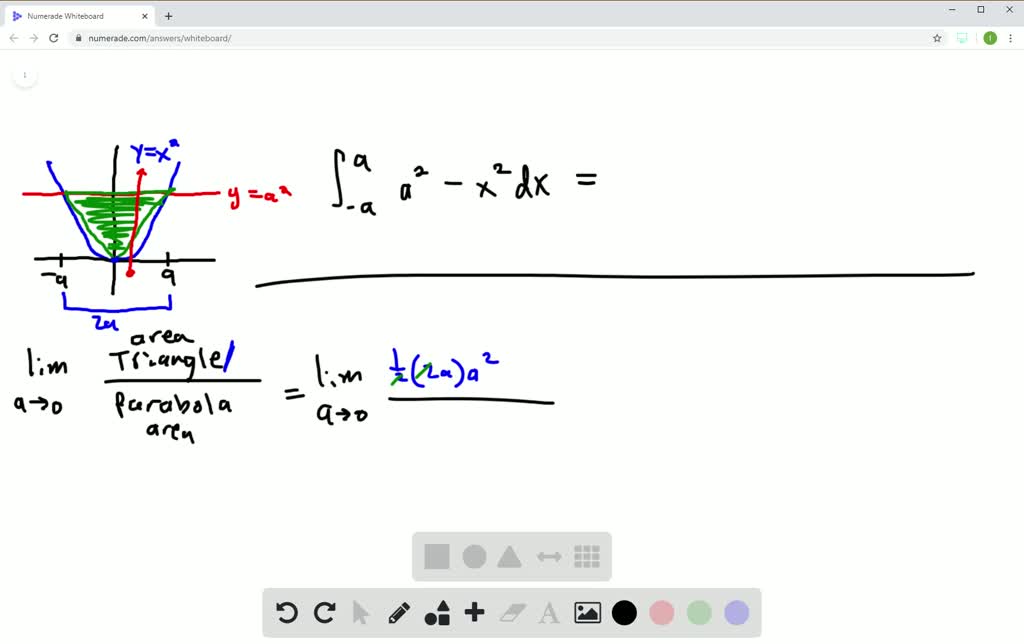
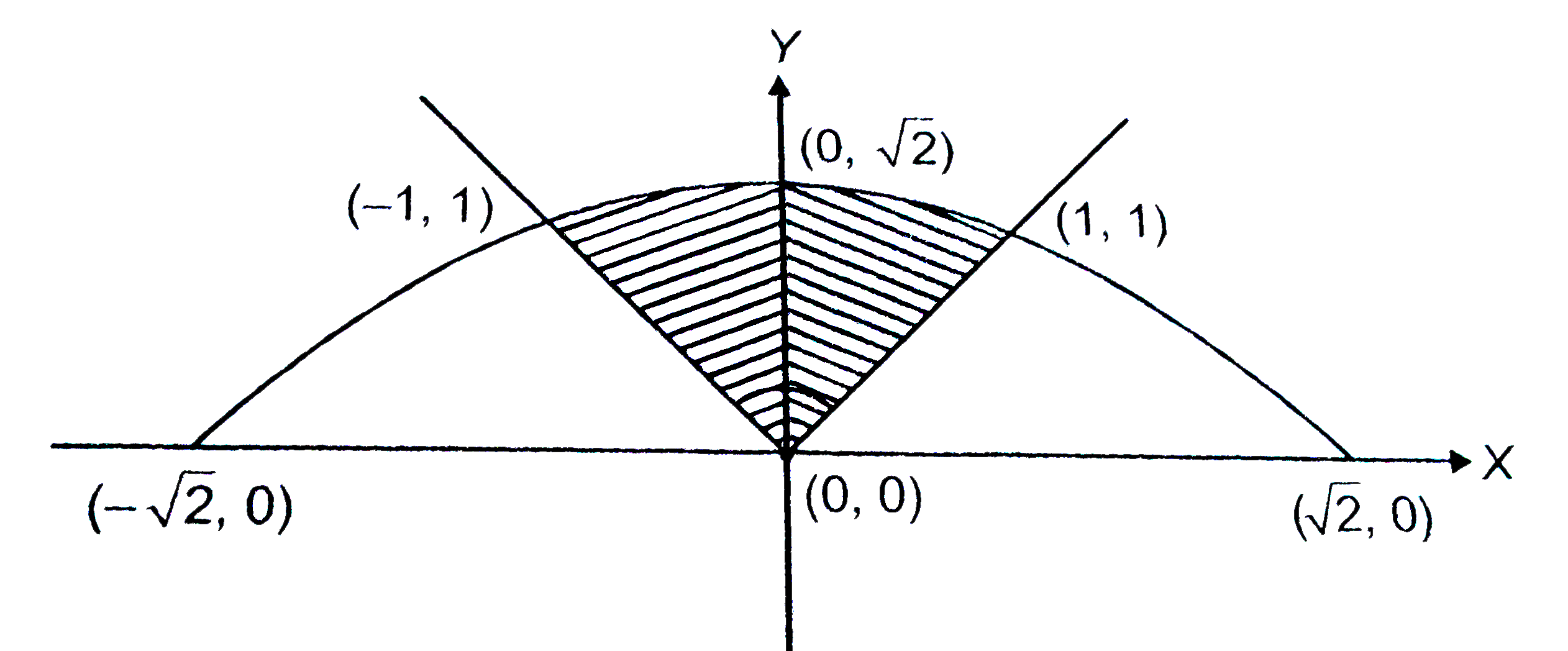
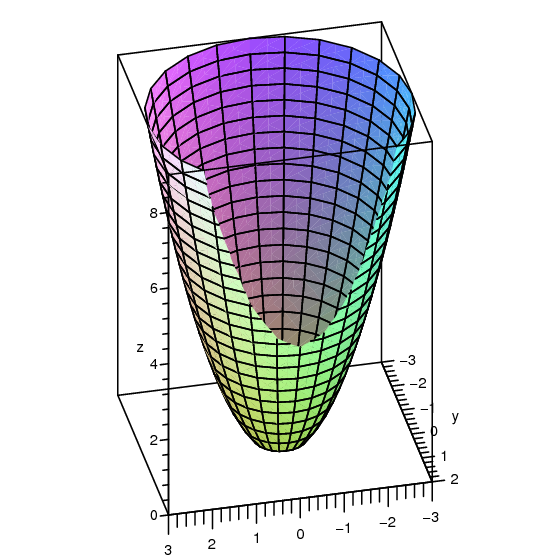
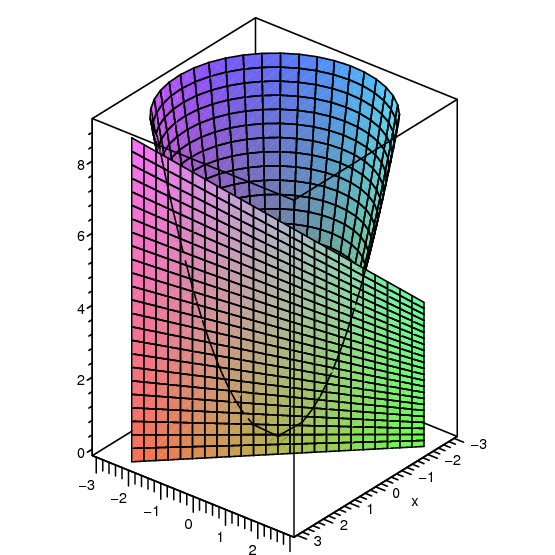
12 Determine the area under the curve y = a x2 2– included between the lines x = 0 and x = a 13 Find the area of the region bounded by y = x and y = x 14 Find the area enclosed by the curve y = –x2 and the straight lilne x y 2 = 0 15 Find the area bounded by the curve y = x , x = 2y 3 in the first quadrant and xaxis Long Answer (LA) 16. So for this case the yintercept is y = (0)2 0x 0 = 0 Transformation left or right Shift left or right Let the vertex of y = x2 −2x → (x2,y2) By including the −2x the new xvertex of y = x2−2x is ( − 1 2) × −2 = 1 = x2 So the transformation for x is x2 − x1 = 1 −0 = 1. Y= x 2 z cut o by the plane y= 25 Solution Surface lies above the disk x 2 z in the xzplane A(S) = Z Z D p f2 x f z 2dA= Z Z p 4x2 4y2 1da Converting to polar coords get Z 2ˇ.
y=x7/(x2)(x3) (i) Let (i) cuts the xaxis at (x, 0) then x7/(x2)(x3) =0 =>x=7 the required point is (7, 0) Differentiating equation (i) wrt x, we get. Homework Statement By using cylindrical coordinate , evaluate ∫ ∫ ∫ zDv , where G is the solid bounded by the cylinder (y^2) (z^2) = 1 , cut by plane of y = x , x = 0 and z = 0 I can understand that the solid formed , was cut by x = 0 , thus the base of the solid formed has circle of (y^2) (z^2) = 1 as base. • ∀x ∈ E, ∀y ∈ F, we have x ≤ y Then, ∃z ∈ R such that x ≤ z, ∀x ∈ E and z ≤ y, ∀y ∈ F Least Upper Bound Theorem Every nonempty subset S of R with an upper bound has a least upper bound (also called supremum) 12 Least Upper Bound Basic Properties.
X and y are the sides of two squares such that y = x x2 Find the rate of change of the area of second square with respect to the area of first square asked in Class XII Maths by nikita74 Expert ( 113k points). Transcript Ex 63, 23 Prove that the curves 𝑥=𝑦2 & 𝑥𝑦=𝑘 cut at right angles if 8𝑘2 = 1We need to show that the curves cut at right angles Two Curve intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other First we Calculate the point of intersection of Curve (1) & (2. Use Stokes’ theorem to evaluate ∫ C 2 x y 2 z d x 2 x 2 y z d y (x 2 y 2 = 2 y i e z j − arctan x k with S as a portion of paraboloid z = 4 − x 2 − y 2 z = 4 − x 2 − y 2 cut off by the xyplane oriented counterclockwise 363 T Use a CAS to evaluate.
Three of the data points — the smallest x value, an x value near the mean, and the largest x value — are labeled with their corresponding leverages As you can see, the two x values furthest away from the mean have the largest leverages (0176 and 0163), while the x value closest to the mean has a smaller leverage (0048) In fact, if we look at a sorted list of the leverages obtained in. X 2 y 2 z 2 = z The bottom of the balloon is modeled by a frustum of a cone (think of an ice cream cone with the pointy end cut off) The radius of the large end of the frustum is 28 28 feet and the radius of the small end of the frustum is 6 6 feet A graph of our balloon model and a crosssectional diagram showing the dimensions are. Solution Let the line y – x 2 = 0 divide the line joining the points A (3, 1) and B (8, 9) in the ratio k1 Let C (x, y) be the point of intersection of these two lines Then by section formula x = (mx 2 nx 1 )/ (mn) y = (my 2 ny 1 )/ (mn) Here (x 1, y 1) = (3, 1) (x 2, y 2) = (8, 9) mn = k1.
The two curves x = y^2 and xy = a^3 cut orthogonally, then a^2 is equal to ← Prev Question Next Question → 0 votes 161k views asked in Mathematics by ShivamK (6k points) The two curves x = y2 and xy = a3 cut orthogonally, then a2 is equal to (A) 1/3.
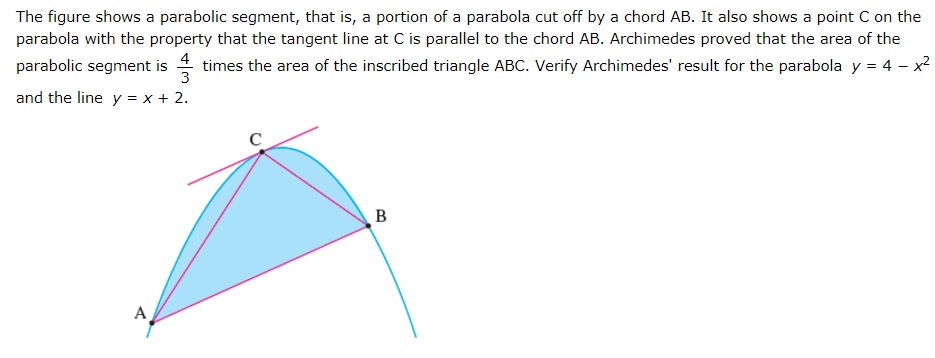
Stewart Calculus 8e Chapter 5 Plus Problems

Snapsolve

2 C X Y X 4 Y 3 0 Is A C 1 Curve With Mfs C 0 Download Scientific Diagram
Yx2 Cut のギャラリー

18 Qs Ans 1 25 Area Sin Find Pubhtml5

Quadratic Graphs Parabolas 1 To Draw A Quadratic
If The Curve Ay X2 7 And X3 Y Cut Orthogonally At 1 1 Then The Value Of A Is Studyrankersonline

Slowness Curve For 64 Yx Cut Linbo 3 Materials Constants From 16 Download Scientific Diagram
Find The Volume Enclosed By The Cylinder Y 2 X And Y X 2 Cut Off By The Planes Z 0 X Y Z 2 Applied Mathematics 2 Shaalaa Com

3 The Equation Of Straight Line Cutting Off An Intercept 2 From Y Axis And Being Equally Inclined To The Axes Are A Y X 2 Y X 2 B Y X 2 Y X 2 C Y X 2 Y X 2 D None

Ex 8 1 7 Find Area Of Smaller Part Of Circle X2 Y2 Cutoff

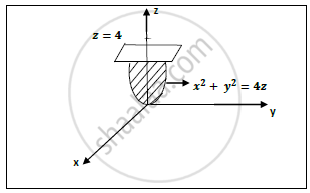
Find The Volume Of The Paraboloid X 2 Y 2 4 Z Cut Off By The Plane 𝒛 𝟒 Applied Mathematics 2 Shaalaa Com
How Do You Write The Definite Integral To Find The Class 12 Maths Cbse
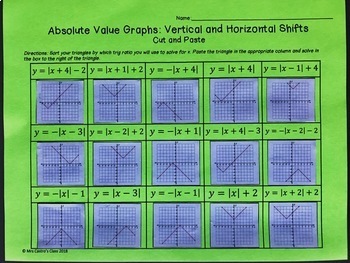
Absolute Value Graphs Horizontal And Vertical Shifts Cut And Paste Activity
1
Household Science In Rural Schools Manner 8 Fasten The Swing Tops Again To The Top Of The Cabinet Drawer The Drawer Front 13 16 X 5 X 143 8 With Lap X

The Graph Of Linear Equation X 2y 2 Cuts The Y Axis At A 2 0 B 0 2 C 0 1 D 1 1 Snapsolve

Find The Point At Which The Curves X Y And Y X Cut Orthogonally Maths Application Of Derivatives Meritnation Com
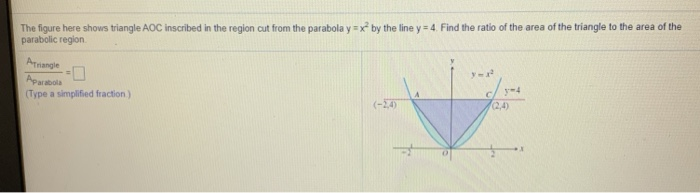
Solved The Figure Here Shows Triangle Aoc Inscribed In The Chegg Com
2
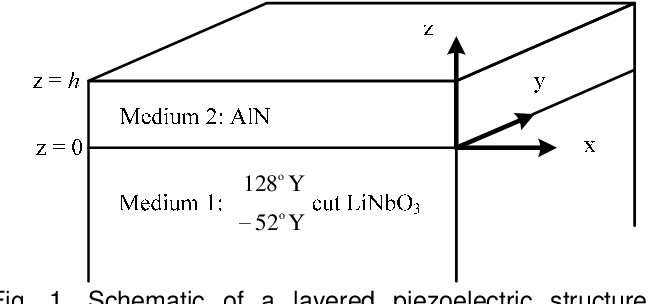
Pdf Propagation Characteristics Of Surface Acoustic Waves In Aln 128 Y X Linbo3 Structures Semantic Scholar

The Figure Shows As Triangle Aob And The Parabola Y X2 Th

Richard Cuts A Peice Of Wood For A Project The First Cut Is Shown And Can Be Represented By The Brainly Com

Ncert Exemplar Class 9 Maths Solutions Chapter 4 Linear Equations In Two Variables 21
1
1
Quadratic Function
Solved Diketahuifungsi F X 2x 3 9x 2 12x 2 Tentukan Titikpotongkurva Dengansumbu Xdansumbu Persamaangarissinggungkurva Di Titik 0 2 Course Hero

Ex 8 1 7 Find Area Of Smaller Part Of Circle X2 Y2 Cutoff
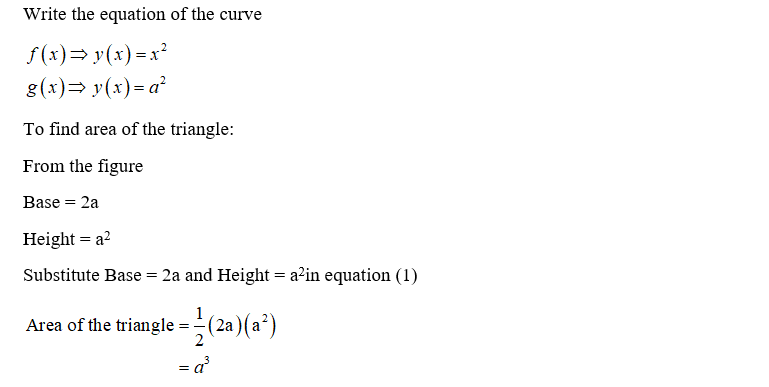
Answered The Figure Here Shows Triangle Aoc Bartleby
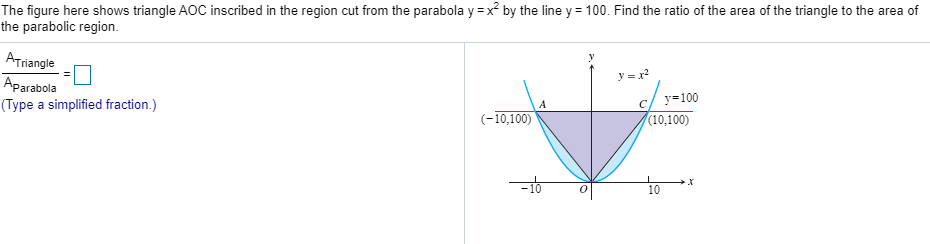
Solved The Figure Here Shows Triangle Aoc Inscribed In The Chegg Com
2
The Keystone System A Text Book On Cutting And Designing Ladies Garments De Seam To Within Yi Inch Of Sand To 3 Apply The Knee Measure From S To T And Inside
What Will Be The Equation Of The Parabola Cuts X Axis At 2 3 And Axis At Point 0 12 Quora

Sheets Of The Riemann Surfaces Of X Y And Y X For The One Cut Download Scientific Diagram
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of
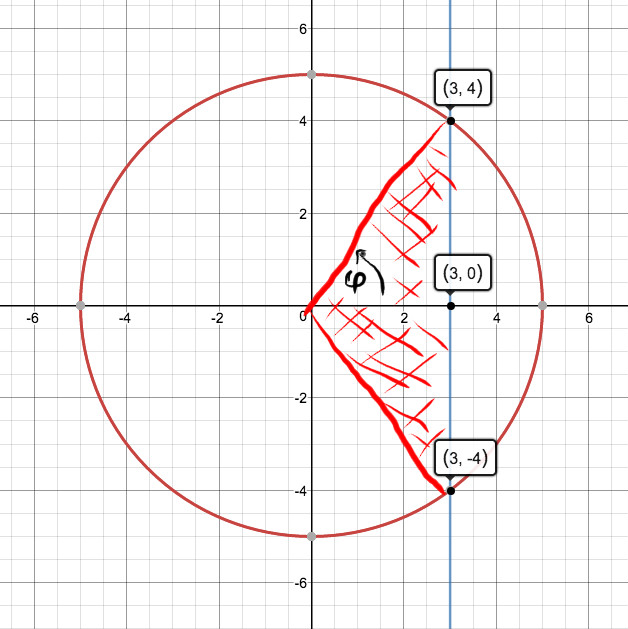
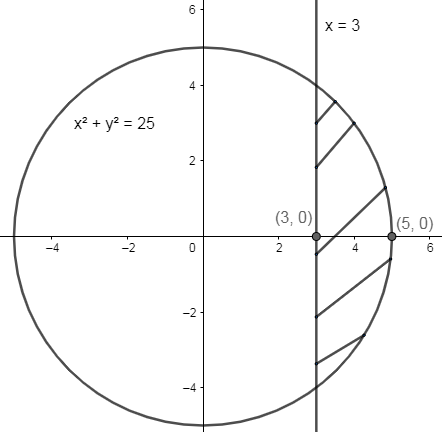
How Do You Write The Definite Integral To Find The Smaller Area Cut From The Circle X 2 Y 2 25 By The Line X 3 Socratic
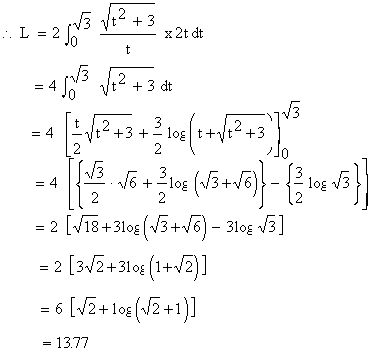
Pinkmonkey Com Calculus Study Guide Section 8 5 Arc Length Rectification

3 Find The Area Of The Minor Segment Of The Circle X 2 Y 2 A 2 Cut Off By The Line X Frac U 2

Taller Calculo B

The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A And B The Normals Drawn To Youtube
1
What Is The Largest Rectangle That Can Be Cut From A Quarter Circle As Shown In The Figure Quora

Saw Grade 128 Y Cut Diameter 4 Inch X 0 5 Mm Ssp Linbo3 Free Pyro Black Wafer 10 Pieces Ost Photonics
B The Diagram Below Shows The Sketch Of The Gauthmath

Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits

Numerical Solutions On Cut Planes Z 0 5 Left And Y X Right At Download Scientific Diagram

The Curves X 3 3xy 2 A And 3x 2 Y Y 3 B Where A And B Are Constants Cut Each Other At An Angle Of
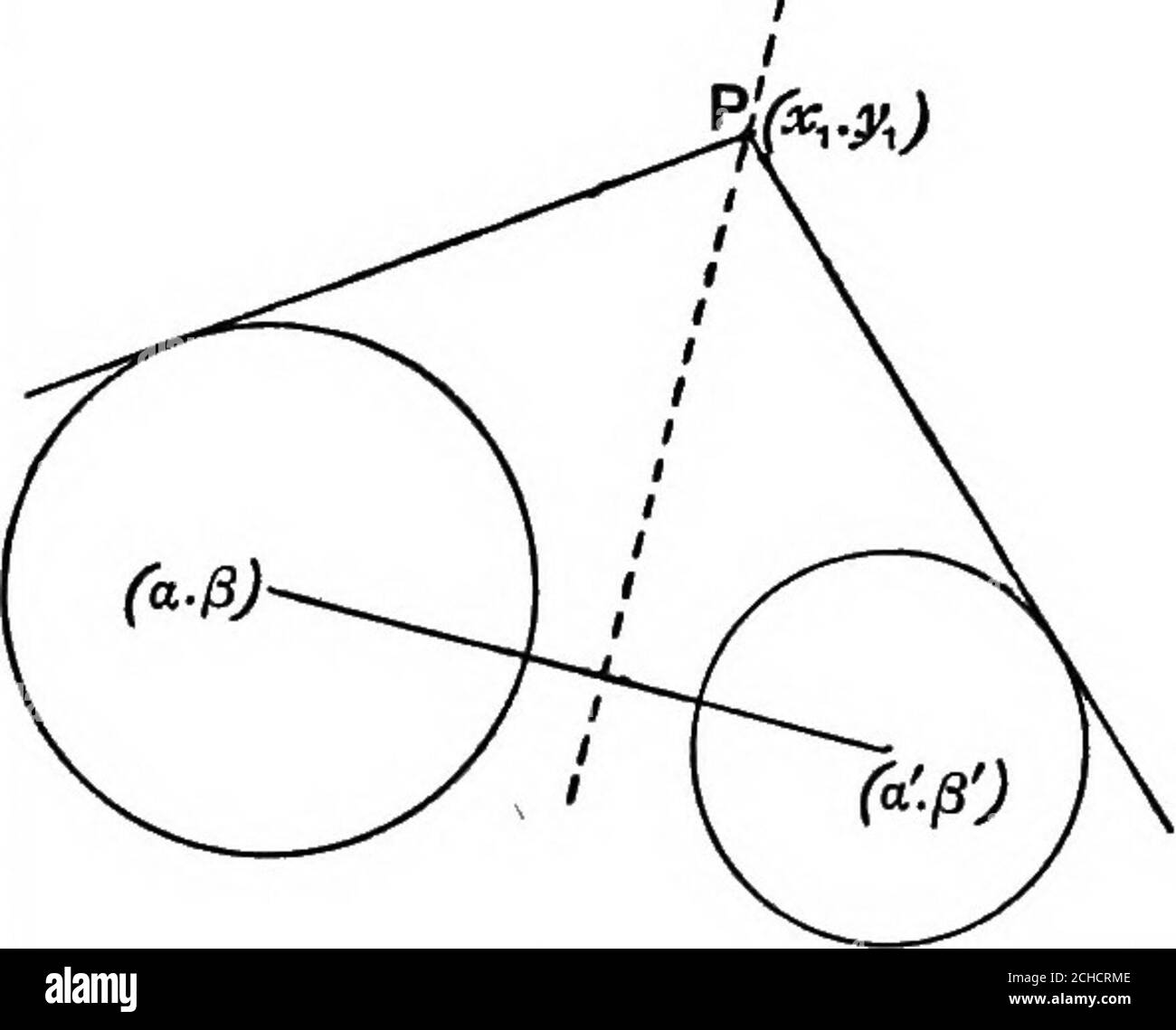
Algebraic Geometry A New Treatise On Analytical Conic Sections At The Point H H Bxg Vii A Orthogonal Circles 105 7 Three Circles Are Described Of Equal Radii R Having
The Parabola Y X 2 C Is To Be Tangent To The Line X Y What Is The Value Of C Quora

How To Find The Volume By Triple Integral Mathematics Stack Exchange

Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits

Geometrical Meaning Ofv X Y X Y X 2 Y 2 Geogebra
Answered The Figure Here Shows Triangle Aoc Bartleby
Quadratic Function Parabola
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of
Algebra Parabola Transformations Of Y X 2 Graphs Match Up 2 Teaching Resources
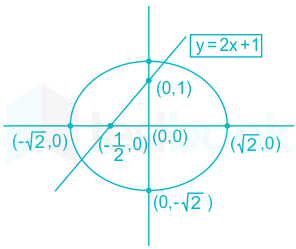
Solved The Length Of The Chord Cut Off By Y 2x 1 From The Circl
Solved 5 6 109 Question Help The Figure Here Shows Chegg Com

The Figure Here Shows Triangle Aoc Inscribed In The Region Cut From The Parabola Y X 2 By The Line Brainly Com

The Length Of The Chord Cut Off By Y 2x 1 From The Circle X2 Y2 Maths Three Dimensional Geometry Meritnation Com
Draw The Graph Of The Linear Equation 3x 4y 6 At What Points Does The Graph Cut The X Axis And The Y Axis Studyrankersonline

Solved Find The Volume Of The Solid Cut From The First Octant By The Surface Z 4 X 2 Y

Answered Find The Absolute Maximum And Minimum Bartleby

The Graph Of Linear Equationx 2y 2 Cuts The Y Aris At Brainly In
Simultaneous Equations Using A Graph
Y2x2 5 ニスヌーピー 壁紙
Count Number Of Triangles Cut By The Given Horizontal And Vertical Line Segments Geeksforgeeks

Find The Length Of The Chord Cut Off By Y 2x 1 From The Circle X 2 Y 2 2 Youtube
Find Area Bounded By Curves Y Sqrt 2 X 2 And Y X
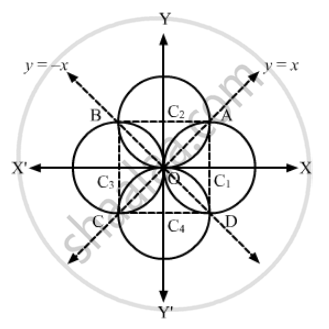
Find The Equations Of The Circles Which Pass Through The Origin And Cut Off Equal Chords Of 2 Units From The Lines Y X And Y X Mathematics Shaalaa Com
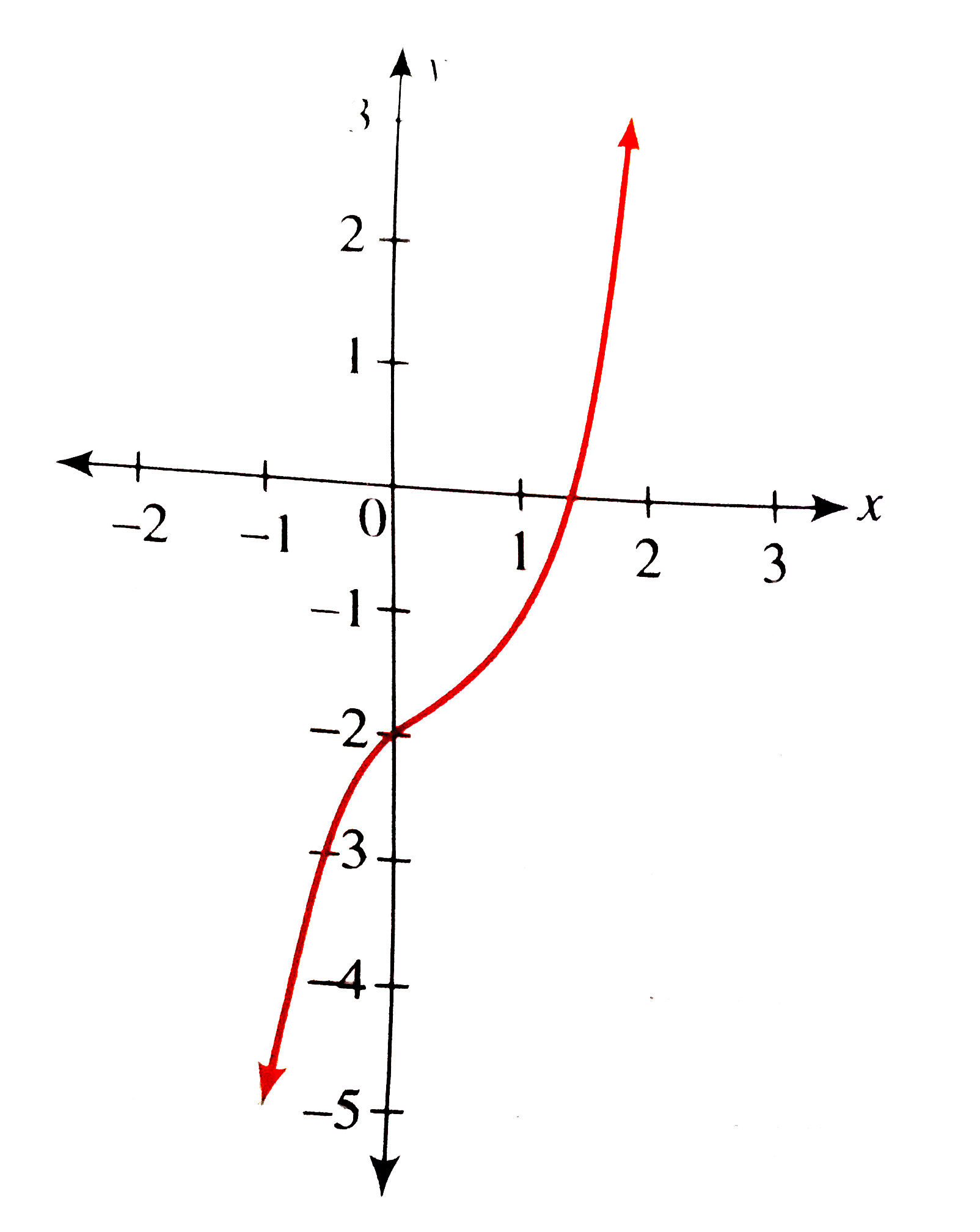
Draw The Graph Of Y X 3 X 2 X 2 And Find The Number Of Real Root S Of The Equation X 3 X 2 X 2 0 Also Locate The Root
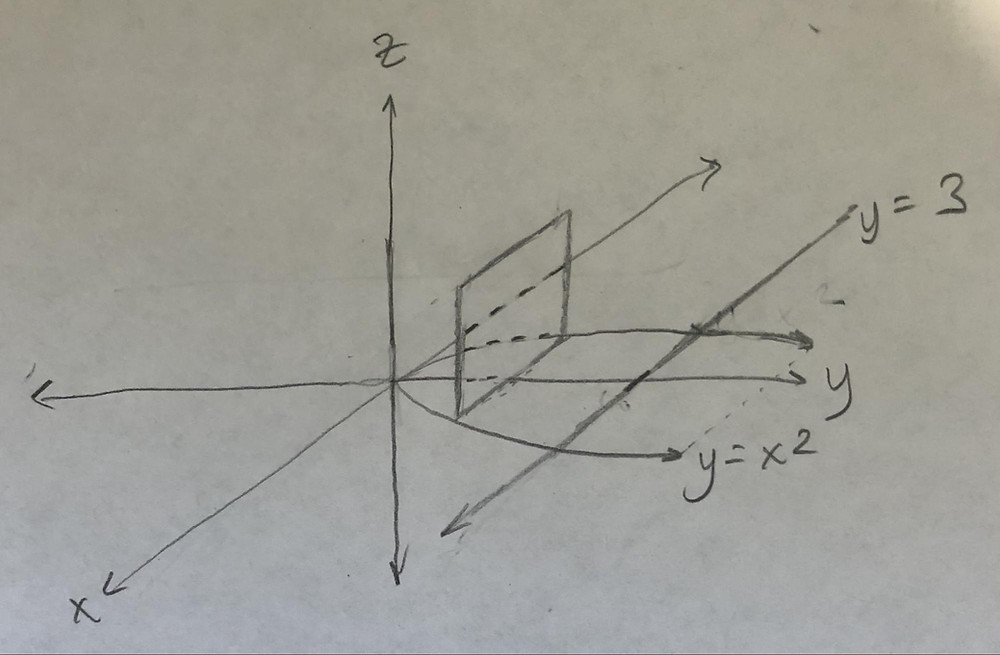
Volume Of A Solid Of Known Cross Section

Solved 5 The Figure Here Shows Triangle Aoc Inscribed In Chegg Com

X 2 Y 2 1 Circle Amazingvoice
14 3 Partial Differentiation
If The Curve Ay X 2 7 And X 3 Y Cut Orthogonally At 1 1 Then The Value Of A Is A 1 B 0 C 6 D 6 Sarthaks Econnect Largest Online Education Community

Find The Area Of The Finite Part Of The Paraboloid Y X 2 Z 2 Cut Off By The Plane Y 25 Hint Project The Surface Onto The Xz Plane Study Com
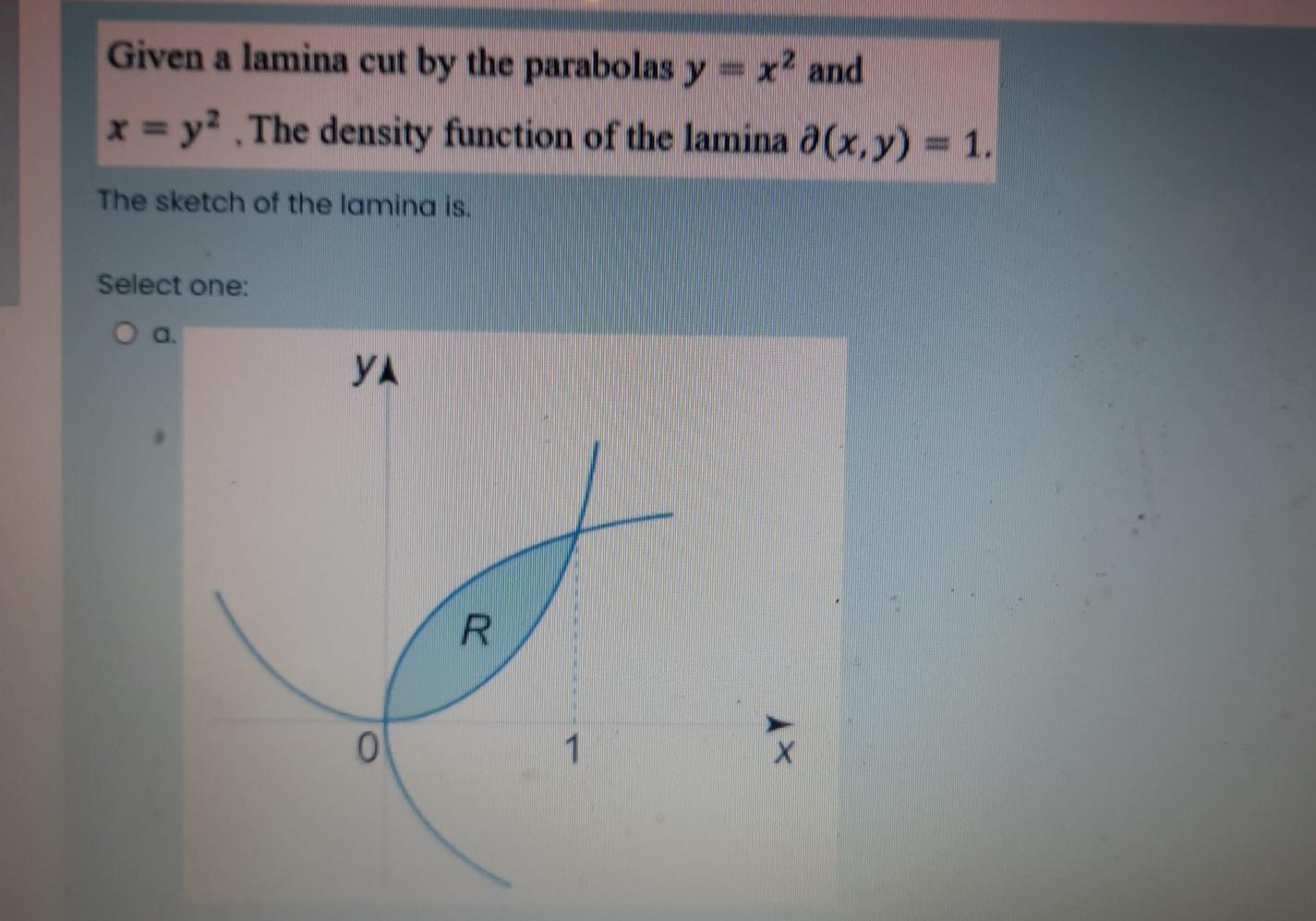
Solved Given A Lamina Cut By The Parabolas Y X2 And X Y2 Chegg Com

2 X2 Y X2 Y 2 Show That The Curves 1 And B A1 Will C Math

14 3 Partial Differentiation Mathematics Libretexts

Solved The Figure Here Shows Triangle Aoc Inscribed In The Chegg Com

Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange
14 3 Partial Differentiation
Show That The Curves 2x Y 2 And 2xy K Cut At Right Angles If K 2 8 Sarthaks Econnect Largest Online Education Community

Draw The Graph Of Y X 2 X 6 And Find Zeroes Justify The Answer
12 Find The Volume Of The Cylindrical Column Standing On The Area Common Tothe Parabolas X Y 2 Y X 2 As Base And Cut Off By The Surface Z 12 Y X 2 Snapsolve

Find The Surface Area Cut From The Plane 2x Y Z 0 By The Cylinder X 2 Y 2 4 Study Com
Sec 4 8 The X And Y Intercepts Ppt Download

Find The Value Of P For Which The Curves X 2 9p 9 Y And X 2 P Y 1 Cut Each Other At Right Angles

Equation Of The Circle Which Cuts The Circle X Y Math
Solved Consider The Graph Ofy X 2 4x1 Course Hero

Ex 6 3 23 Prove That X Y2 Xy K Cut At Right Angles
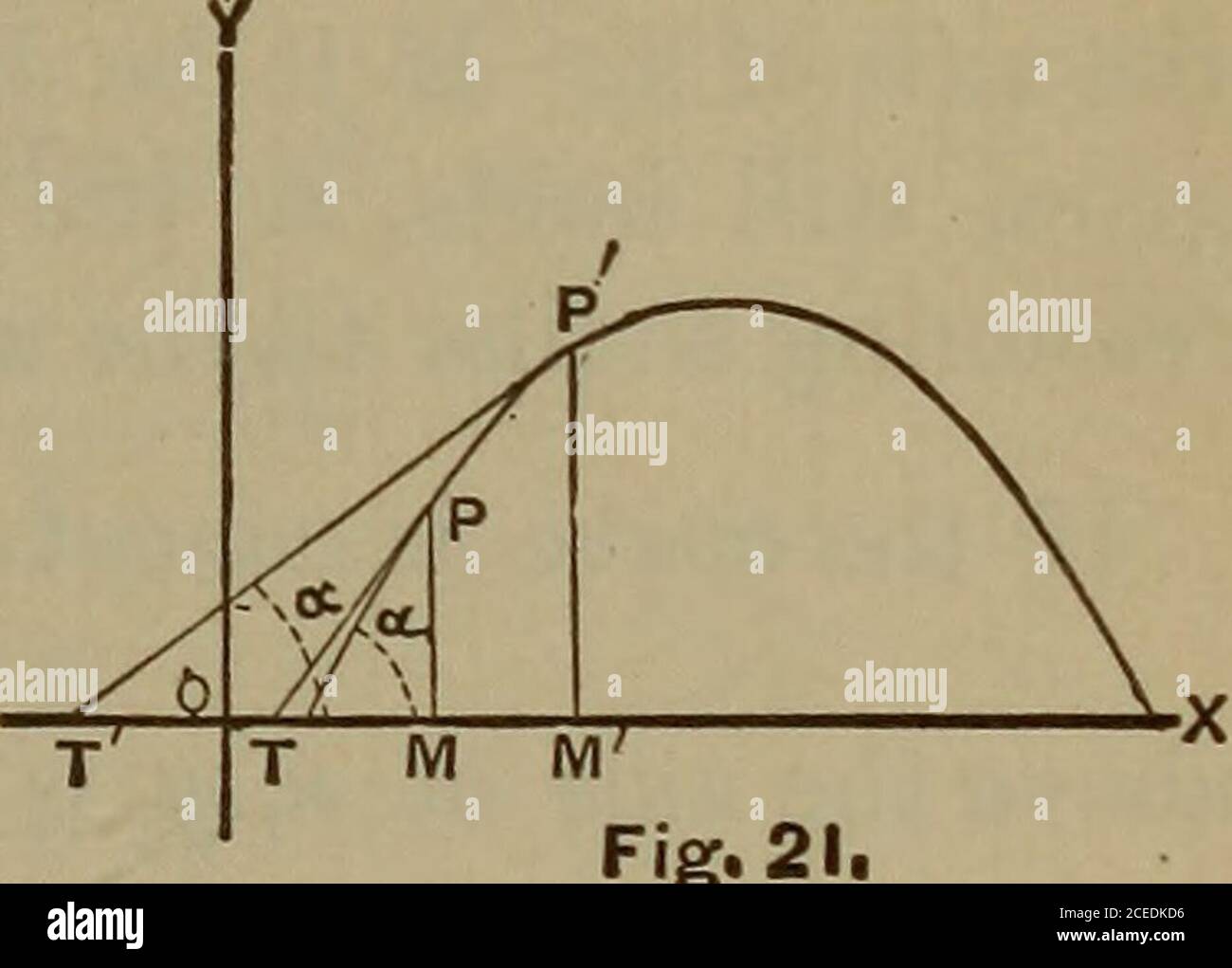
An Elementary Treatise On The Differential And Integral Calculus 21 At What Angle Does Y2 2ax Cut X3 3axy Y3 0 Cot 1 A 4 22 Examine Y2 2x
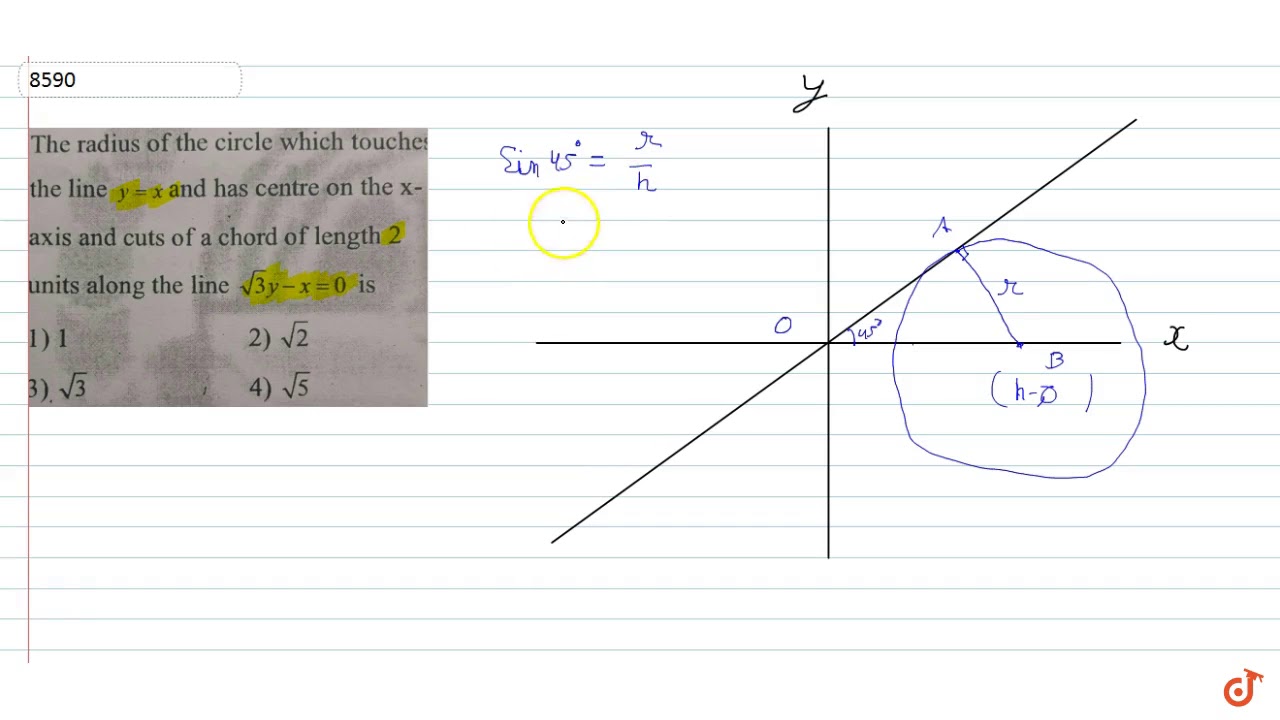
The Radius Of The Circle Touches The Line Y X And Has Centre On The X Axis And Cuts A Chord Of Youtube

Calculus Volume Integral Mathematics Stack Exchange
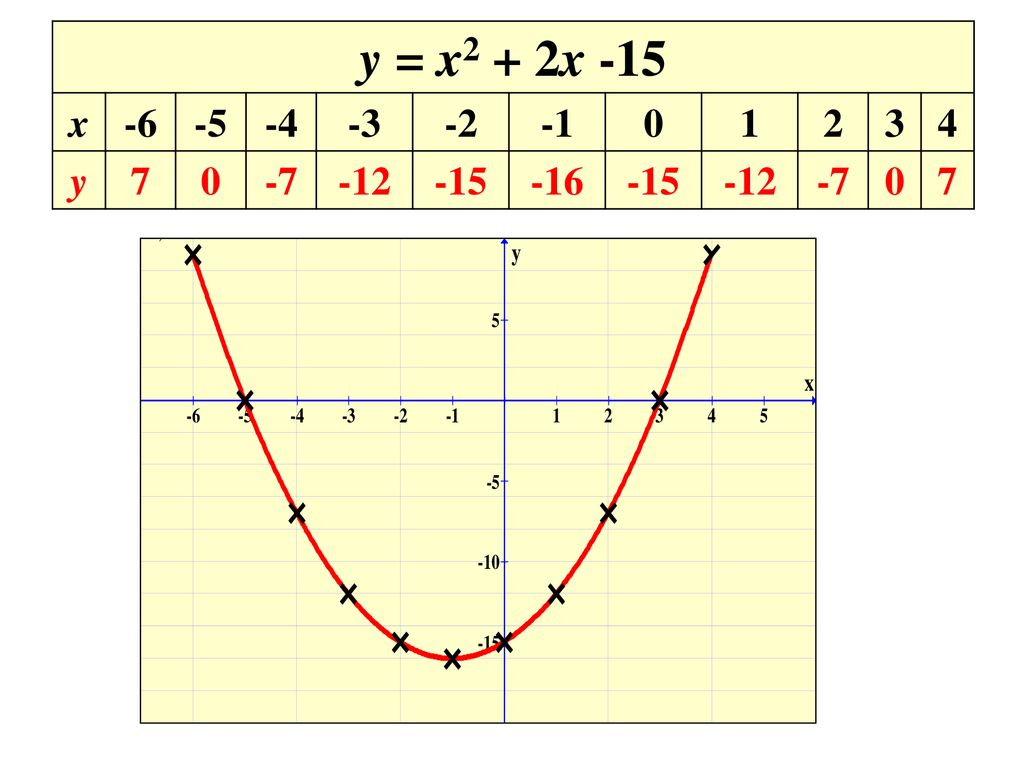
Quadratic Graphs Parabolas Ppt Download
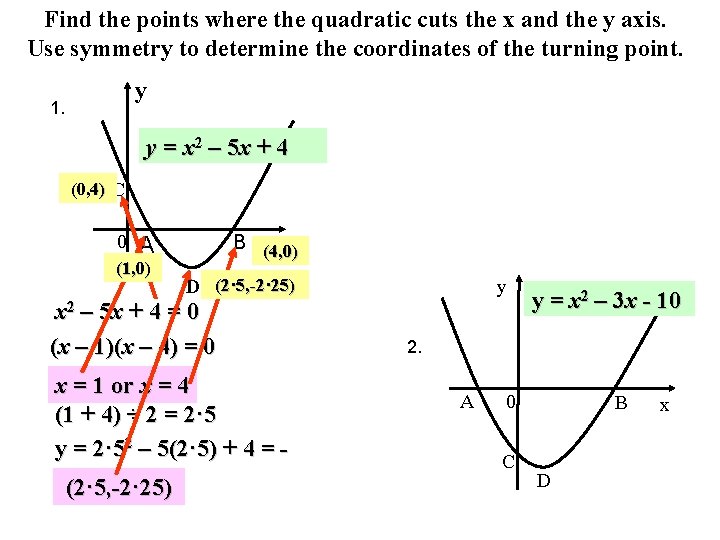
Quadratic Graphs Parabolas 1 To Draw A Quadratic

11 A Digraph With 2 Cut X Y Neither Of The Bridges Of This 2 Cut Download Scientific Diagram
Figure 3 Graph Of Dependency For A Function With An Unsymmetrical Maximum Cut On The Right Y X2 To The Left Of The Maximum Y 0 7 X2 To The Right Of The Maximum
Perseus Iies Su Se
Find The Area Of The Segment Cut Off From The Parabola Y 2 2x By The Line Y 4x 1 Sarthaks Econnect Largest Online Education Community

7 3 Equation Of A Tangent To A Circle Analytical Geometry Siyavula

Find The Area Of The Smaller Part Of The Circle X 2 Y 2 A 2 Cut Off By The Line X A Sqrt 2 Youtube

Int Int B Int Dv Where B Is The Wedge Cut From The Cylinder X 2 Y 2 1 By The Planes Z 0 And Z Y Study Com




