ひし形 の 定理
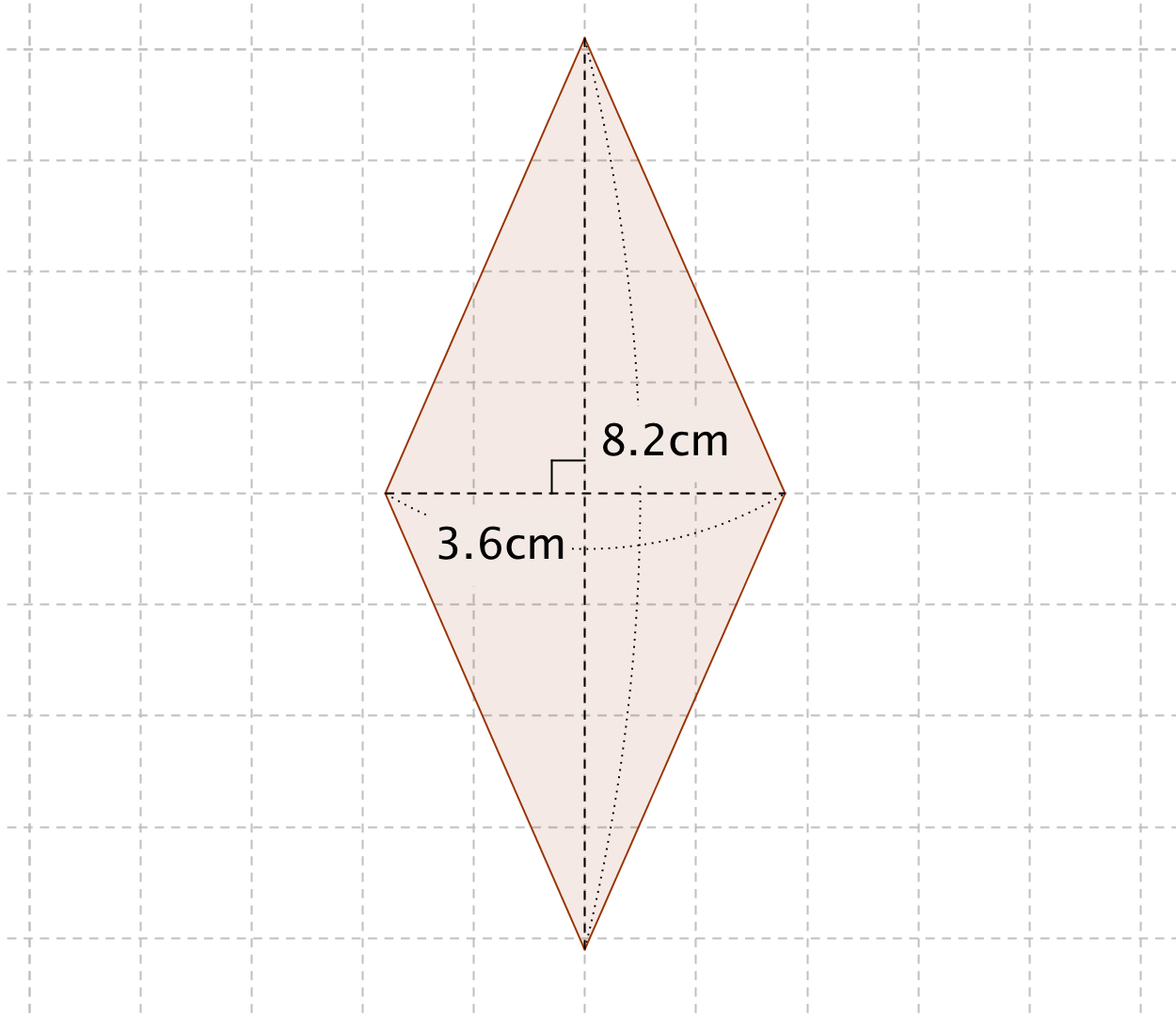
ひし形の面積を求める公式は ひし形の面積 対角線 対角線 ひ し 形 の 面 積 = 対 角 線 × 対 角 線 ÷ 2 なので、 ひし形の面積 ひ し 形 の 面 積 = 36 × ÷ 2 = 2952 ÷ 2 = 1476 ( c m 2) になります。.

ひし形 の 定理. 変換の公式を覚えていれば、わりと楽に解答できます。 鳳テブナンの定理で解く 電圧降下の考え方を理解していれば簡単に解けます。 この3つが主な解き方となります。3の鳳テブナンの定理については、別のページで解説します。 キルヒホッフの法則で解く. 3分でわかる!ひし形(菱形)の定義 中2数学 中2数学多項式の計算問題を瞬殺できる3つのステップ 中1数学 コンパスと定規で作図三角形の書き方がわかる3つのステップ 中3数学. ひし形は、同じ長さの辺が直角ではない状態で連続した四角形でした。 辺と辺の触れ合う角の角度が、直角の場合は正方形と言います。 正方形であれば簡単に書けそうですが、ひし形はどうやって作図すればいいのでしょうか? コンパスを使って作図する 最もオーソドックスな作図の方法は、コンパスを使います。 「コンパスなんて小学校に通っていた時代以来、使っていない」と.
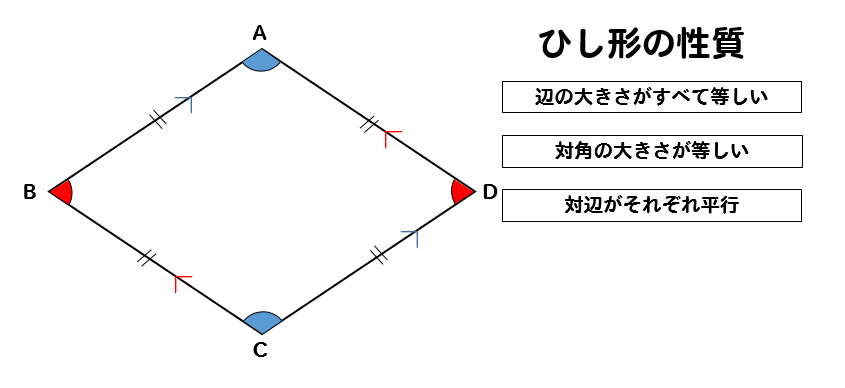
図形の定義及び性質〔参考:算数教科書の定義・定理辞典 著 志水廣 啓林館わくわく算数〕 ひし形 すべての辺の長さが等しい四角形 向かい合う辺が平行である。. ひし形(菱形)とは? 定義 ひし形(菱形)とは、 つの辺の長さがすべて等しい四角形 のことをいいます。 この定義に従うと、 正方形 もひし形の一種ですね。 まずはこの定義をしっかり覚えておきましょう。 ひし形の面積の公式 次に、ひし形の面積を求める公式を確認しましょう。 ひし形の面積の公式 ひし形の 本の対角線を 、 とおくと、面積 は ひし形の面積 対角線 対角線. ひし形の 定義・・・ 4辺が等しい平行四辺形 定理・・・ 2対角線は垂直に交わる といった感じでしょうか。.
17/1/ 中2数学 スポンサーリンク 定期テストは出題されて、直接的に、入試に出題されることがほとんどないのが、「図形の定義と性質のまとめ」です。 定期テストでは、覚えておけば、得点出来るところですので、数学というより、暗記です。 入試で. 図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し い。. そんなひし形の定義はしっかりと覚えておかなければならない重要な項目です。 ひし形の定義ですが、4つの辺が全て等しい四角形です。 大人の方も正確には答えられないかもしれませんね。 このひし形ですが、いくつかの特徴を持っています。 しっかりと特徴をおさえておくことで、様々なパターンの図形問題に対応していくことが出来ます。 まず、 平行四辺形 の一種でもあるということです。.
ちなみに、長方形・正方形・ひし形の定義は全て答えられますか? あいまいだなと思った方は中学2年生の教科書を見返してみましょう。 図形問題が苦手な方は、 上記以外にも様々な図形の定義、定理を1つ1つしっかりと理解して、. 台形の中でも、 組の辺が共に平行となっている四角形は「平行四辺形」です。 さらに、平行四辺形のうち、すべての角が ならば「長方形」、すべての辺が等しければ「ひし形」、そのどちらも満たすならば「正方形」です。 平行四辺形・長方形・ひし形・正方形は、実はどれも台形の一種と言えますね。 台形の面積の公式 台形の面積を求める公式は次のとおりです。 台形の面積の公. このように すべての辺が等しい四角形 のことをひし形といいます。 ここでちょっと考えて欲しいのが ひし形っていうのは、すべての辺が等しい四角形。 ということは、ちょっと見方を変えると 「2組の向かい合う辺がそれぞれ等しい」 ってことでもある。.
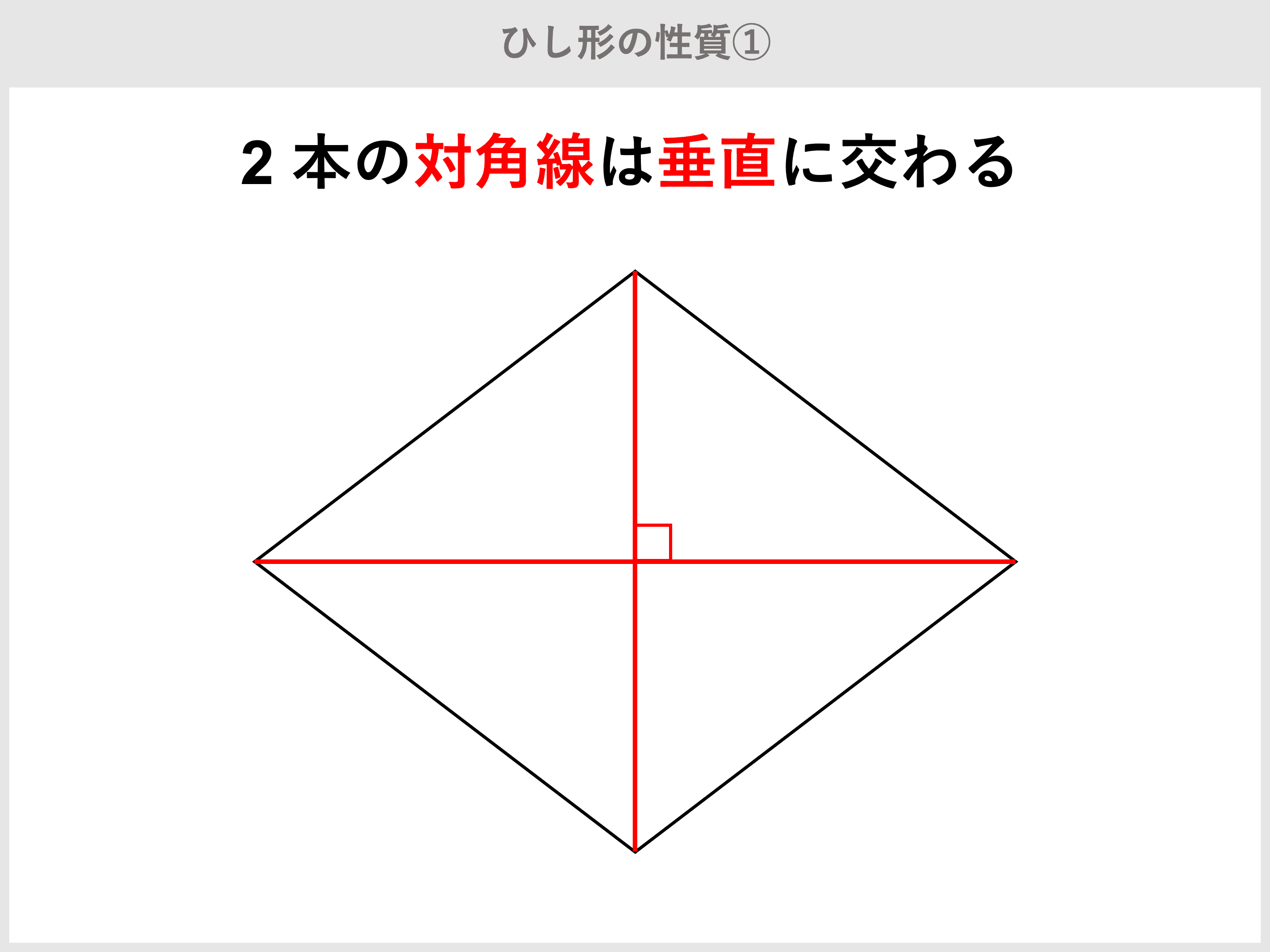
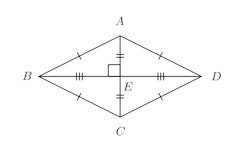
〔ひし形の対角線の性質〕ひし形の対角線は(それぞれの中点で)垂直に交わる。 〔証明〕ひし形abcdの対角線ac,bdの交点をoとする。 aboと ( )において ひし形の定義から. 上の「平行線と線分の比の定理」の逆も成り立てば、もっと鋭い武器になりますね! すなわち、「ここと、ここの比が同じ ならば 、2直線は 平行である !. テブナンの定理の問題集 21年10月28日 直流回路 スポンサーリンク 電流を求めたい部分を切り離します。 等価電源 V 0 を求める。 等価抵抗 R 0 を求める。 (回路内部の電源をすべて短絡する) 等価回路に変換する。.
ひし形の定義は 「4つの辺がすべて等しい四角形」 正方形の定義は 正方形の定理 「4つの角がすべて等しく、 「正方形の対角線は、 4つの辺がすべて等しい四角形」 長方形の定理 「長方形の対角線は、長さが等しい。」 ひし形の定理 「ひし形の対角線は. A^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた. ひし形は平行四辺形の一種です。 向かい合う辺が平行な四角形が平行四辺形ですが、さらに 4 4 辺の長さが等しい図形がひし形になります。 ( 4 4 辺の長さが等しい時は向かい合う辺は必ず平行) 今回は対角線の長さが分かっている時のひし形の面積の求め方を説明していきます。 2 2 つの方法で説明することができるので、ぜひ小学生のお子さんに教える際などに参考にしてください。 目次 非.
ひし形の定義、定理(特徴・性質)は、 ③ 対角線が直交 する ですね。 そして、 ① ひし形の面積 = 底辺×高さ または ② ひし形の面積 = \. 定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形はひし形である. 対角線の長さが等しく、それぞれの中点で交わるとき、長方形になる。(証明) ひし形になる条件 対角線がそれぞれの中点で垂直に交わるとき、ひし形になる。(証明) 問題 1 平行四辺形abcdが、次の条件をもつと、それぞれ、どんな四角形になりますか。.
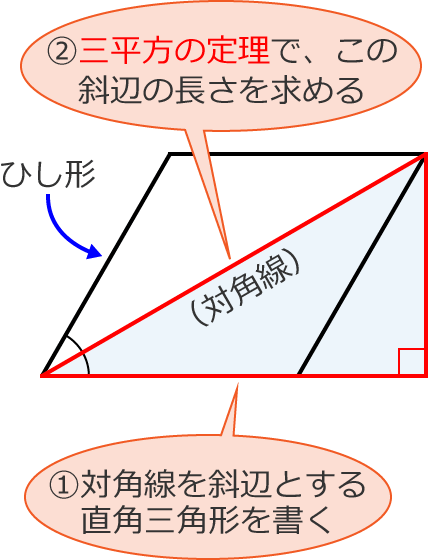
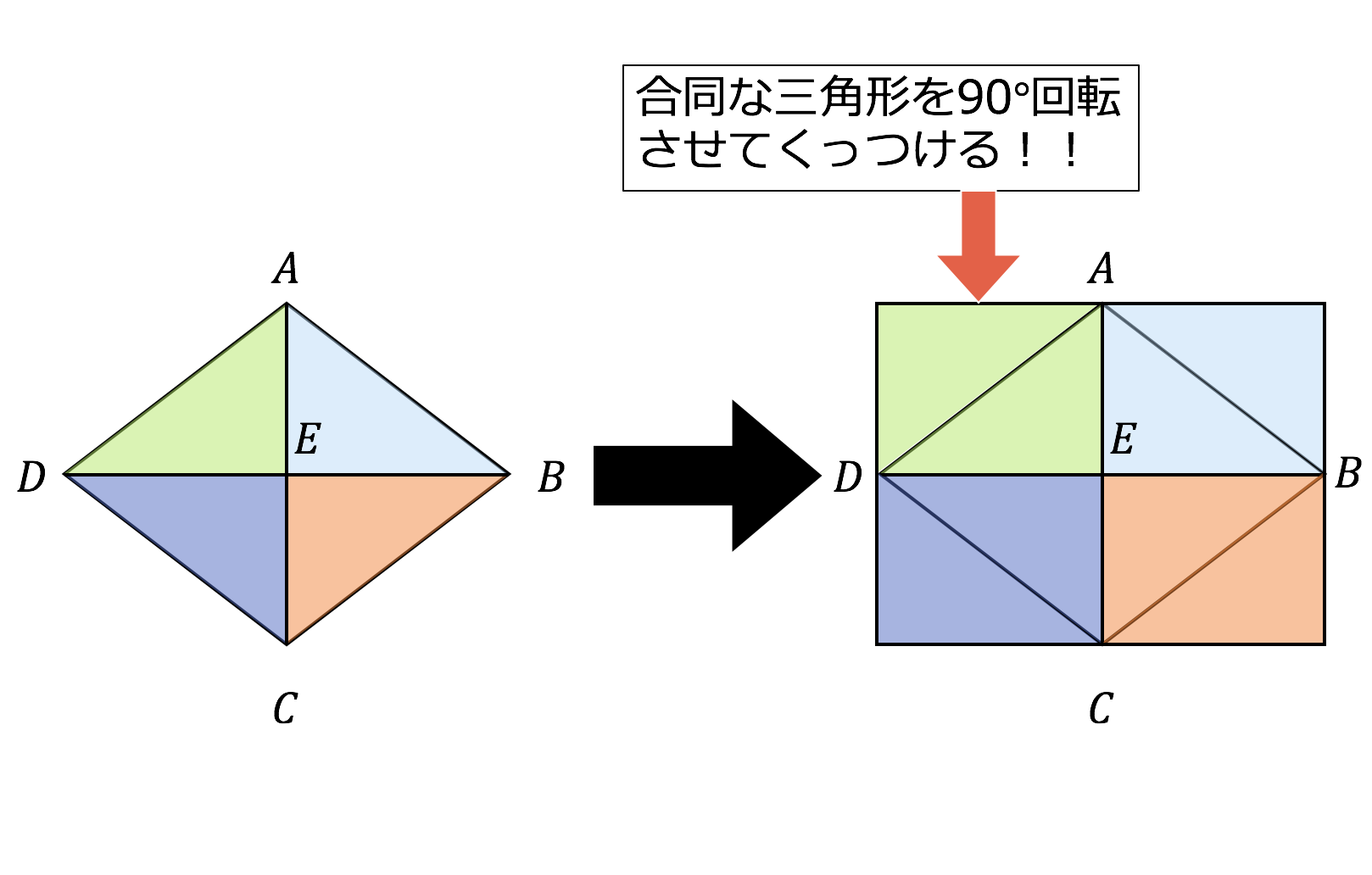
長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については 長方形 が 『対角線の長さが等しい』 、 ひし形 が 『対角線が直交する』 という性質があります。 そして正方形は平行四辺形でもあり、長方形でもあり、ひし形でもあるので. ひし形の定義は「全ての辺の長さが等しい四角形」であり、「2つの対角線は互いに垂直に交わる」という性質があります。 さて、下の図のようにひし形を2つの対角線で区切ると、4つの直角三角形に分けることができます。 この三角形はすべて同じ形(合同)になります。 ひし形を2つの対角線で4つの直角三角形に分けた この4つの直角三角形を並び替えると、下の図のように長方形にすることが出. 方を引き出すことができる。また、この課題学習を三平方の定理を学習した後に実施すれば、 (ウ)の対角線の長さを正確に求めることかできる。 三平方の定理を利用して、ひし形pbqdの面積を求める。 ap=ズ(cm)とする。 d bd2=122+ ゴ8 bd>0⊥車り bd.
ひし形の定義は 全ての辺の長さが等しい四角形 です。 下図をみてください。 これがひし形です。 上図のように4つの辺の長さが等しい四角形です。 角度の大きさは一致しなくても良いです。 また、似た図形に「平行四辺形(へいこうしへんけい)」があります。 下図のように見た目は似ていますが、平行四辺形の定義は「2組の辺の長さ等しい四角形」です。 平行四辺形は全ての辺の長さが等しい. 長方形の定理の逆 四角形で対角線の長さが等しければ 長方形である × 長方形の定理の逆 ~平行四辺形で対角線の長さが等しければ 長方形である ひし形の定理の逆 四角形で対角線が垂直に交われば ひし形である × ひし形の定理の逆. ※ひし形の定義式との関係 を,証明を読み直してとら え,図形の性質を証明して いる。(ノート・発言) 発展の問.については,次 時に短時間で答え合わせを 行う。.
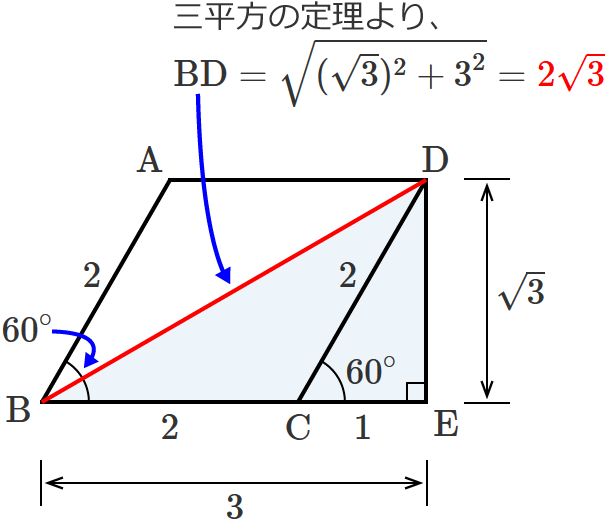
ひし形の対角線の長さの求め方
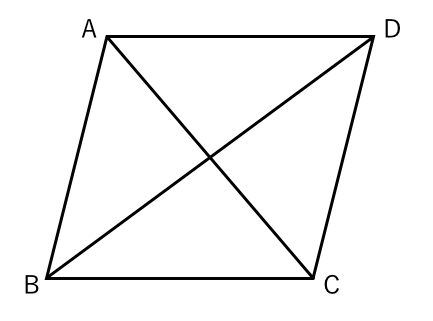
ひし形についての問題 苦手な数学を簡単に
この2番の答えが何故ひし形になるのか分からないです中点連結定理 Yahoo 知恵袋
ひし形 の 定理 のギャラリー

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
Tossランド 特別な平行四辺形
Ed City Daito Osaka Jp

フェルマーの最終定理並ぶひし形のアイコン のイラスト素材 ベクタ Image

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
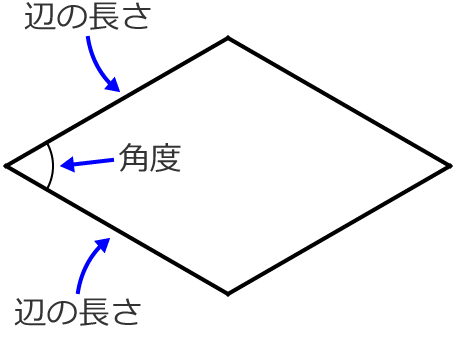
ひし形の対角線の長さの求め方

菱形定義 平行四辺形 ひし形 長方形 正方形の違い Vsrius
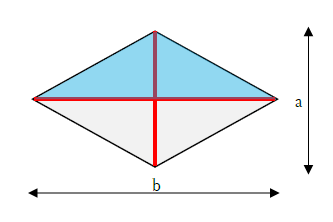
ひし形の面積は 1分でわかる求め方 公式 辺の長さ 対角線との関係

3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
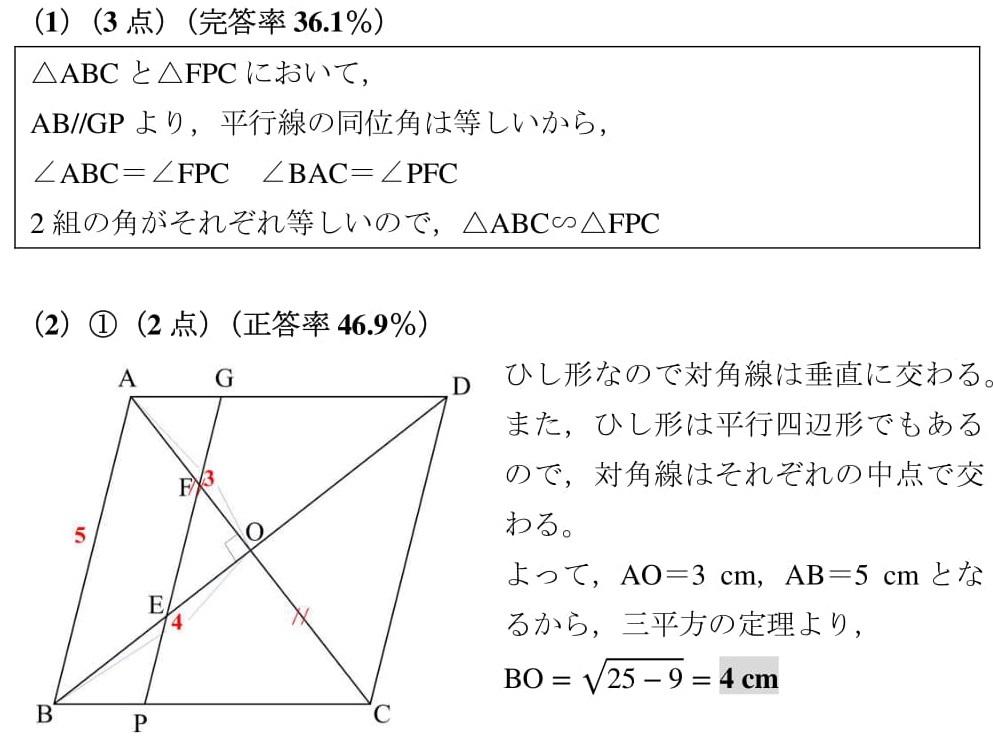
正答率0 1 素直に菱形 21年大分県 高校入試 数学 良問 難問

ひし形の定義 性質 条件 Youtube
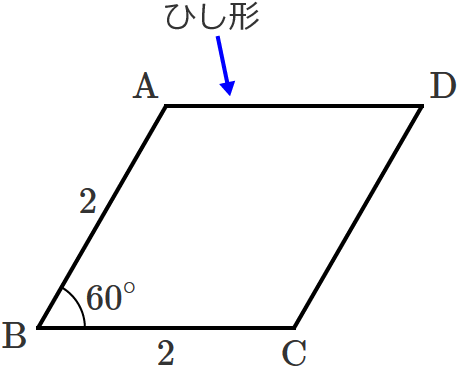
ひし形の対角線の長さの求め方
Tsumugi Ne Jp
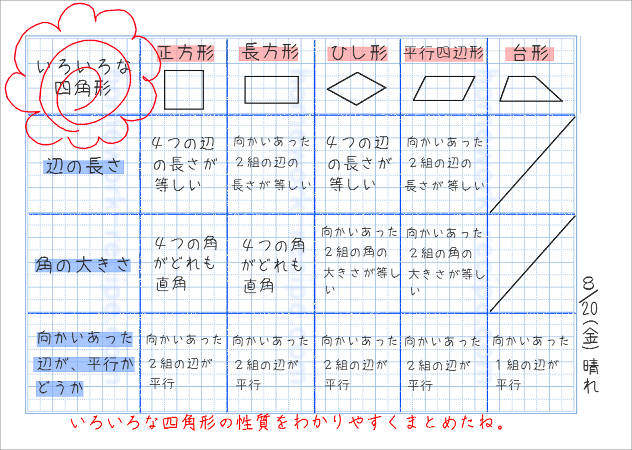
いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ

ひし形についての問題 苦手な数学を簡単に

1 と 2 がなぜそうなるのか理由を教えていただきたいです Clearnote
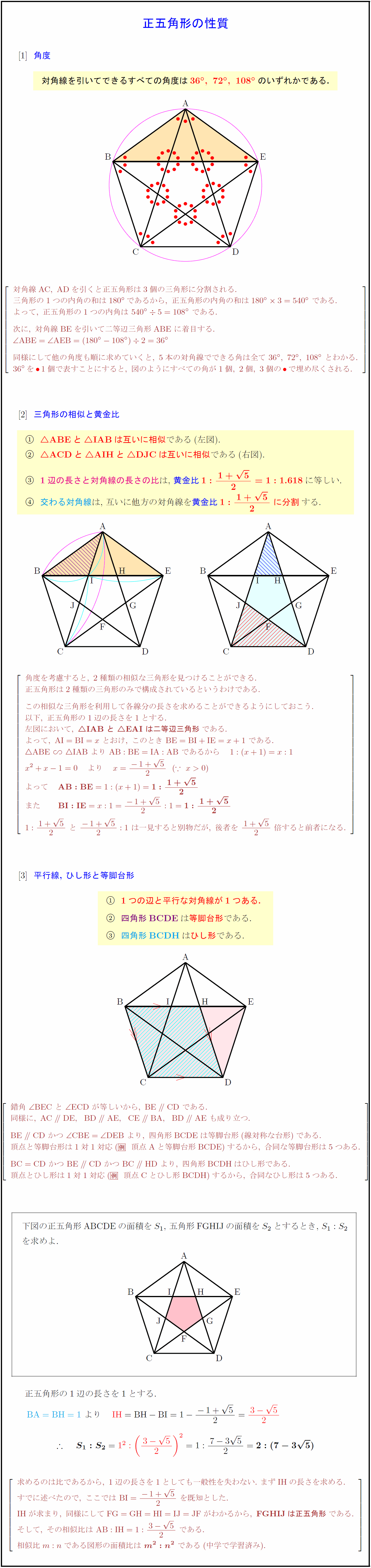
高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月
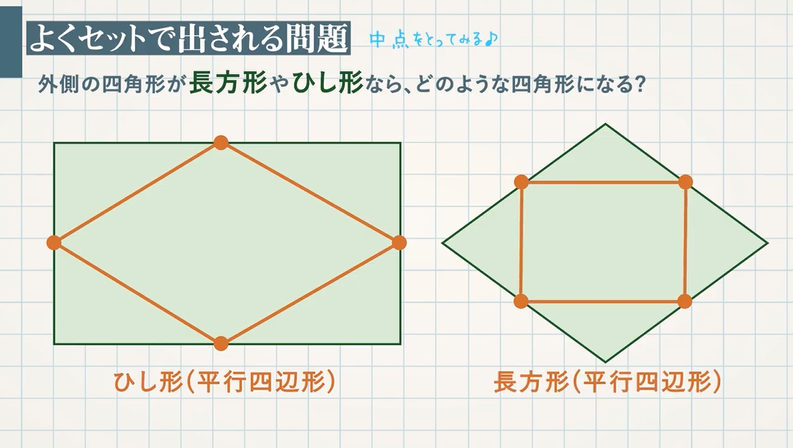
中点連結定理を使った平行四辺形であることの証明 教遊者
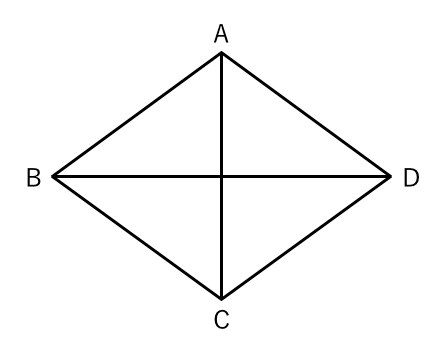
ひし形についての問題 苦手な数学を簡単に
Ed City Daito Osaka Jp

ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ
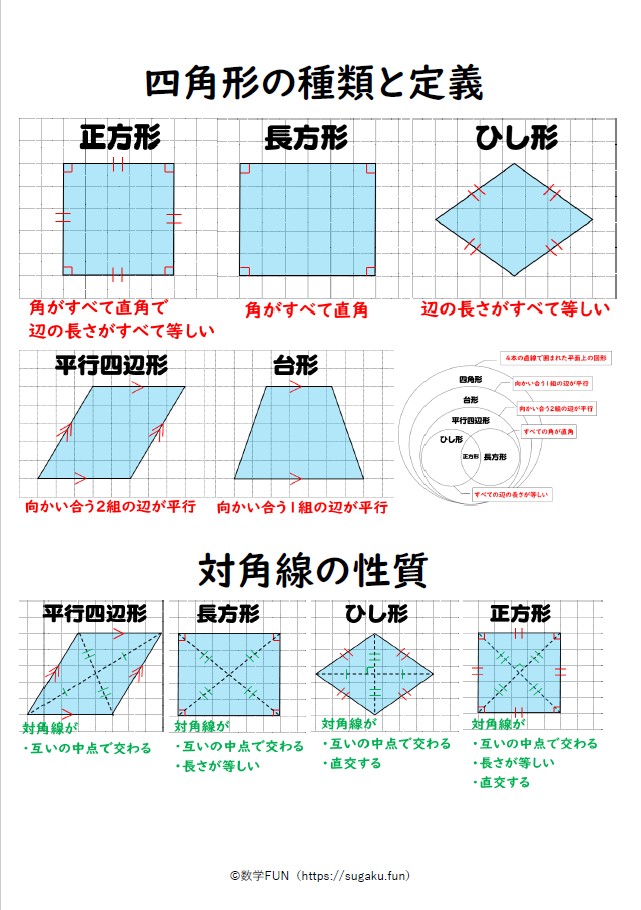
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

菱形 Wikipedia
長方形 ひし形 円 等脚台形 直角三角形 正方形 の定理と定理を教えてくだ Yahoo 知恵袋
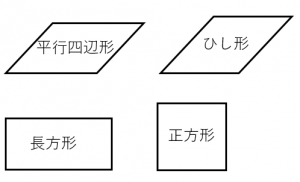
平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
受験テクニック ひし形の面積は何 ですか Youtube
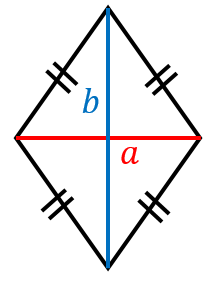
ひし形の面積を求める方法と例題 具体例で学ぶ数学

空間の切断面の面積を求める問題 無料で使える中学学習プリント

中学校数学 証明のコツ 四角形の性質

ひし形の面積の求め方 公式と計算例
勉強しよう数学 ひし形の対角線の直交の公式

高校数学b 角の二等分線のベクトル2パターン 受験の月
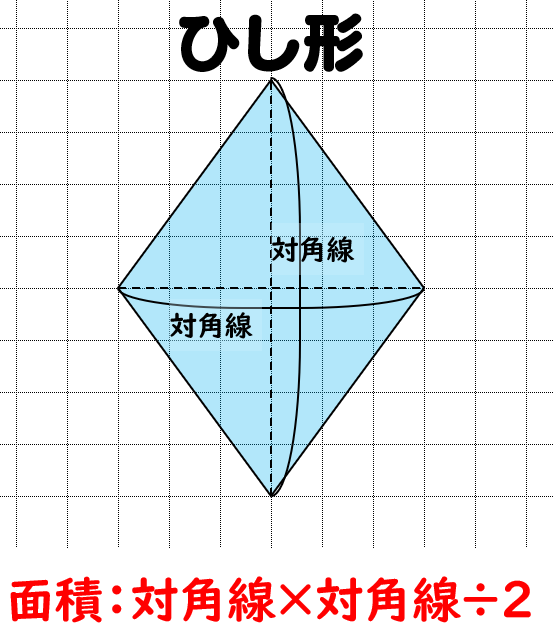
ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

中点連結定理を利用した証明 チーム エン
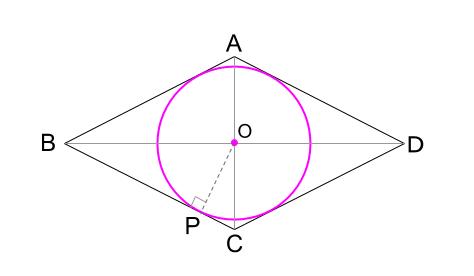
作図 ひし形の内接円 中学数学の無料オンライン学習サイトchu Su
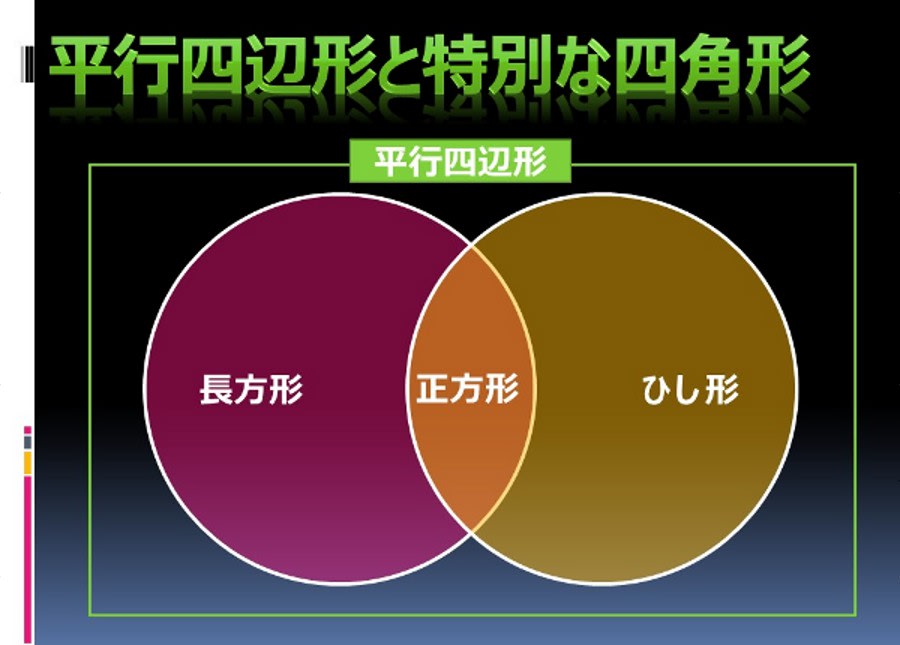
高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座

高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
1
3

ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ
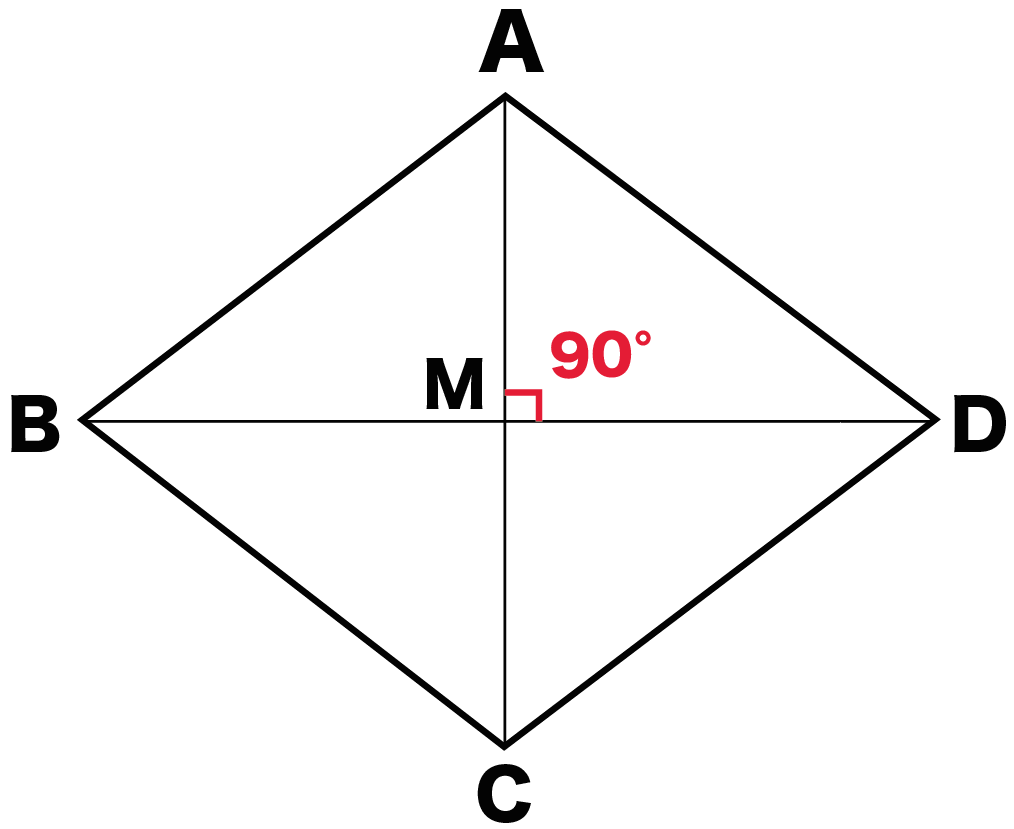
ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく
2 の答えがひし形になることを中点連結定理を用いて証明したいのですが 模範 Yahoo 知恵袋

四角形の4つの辺の中点を結んでできる四角形
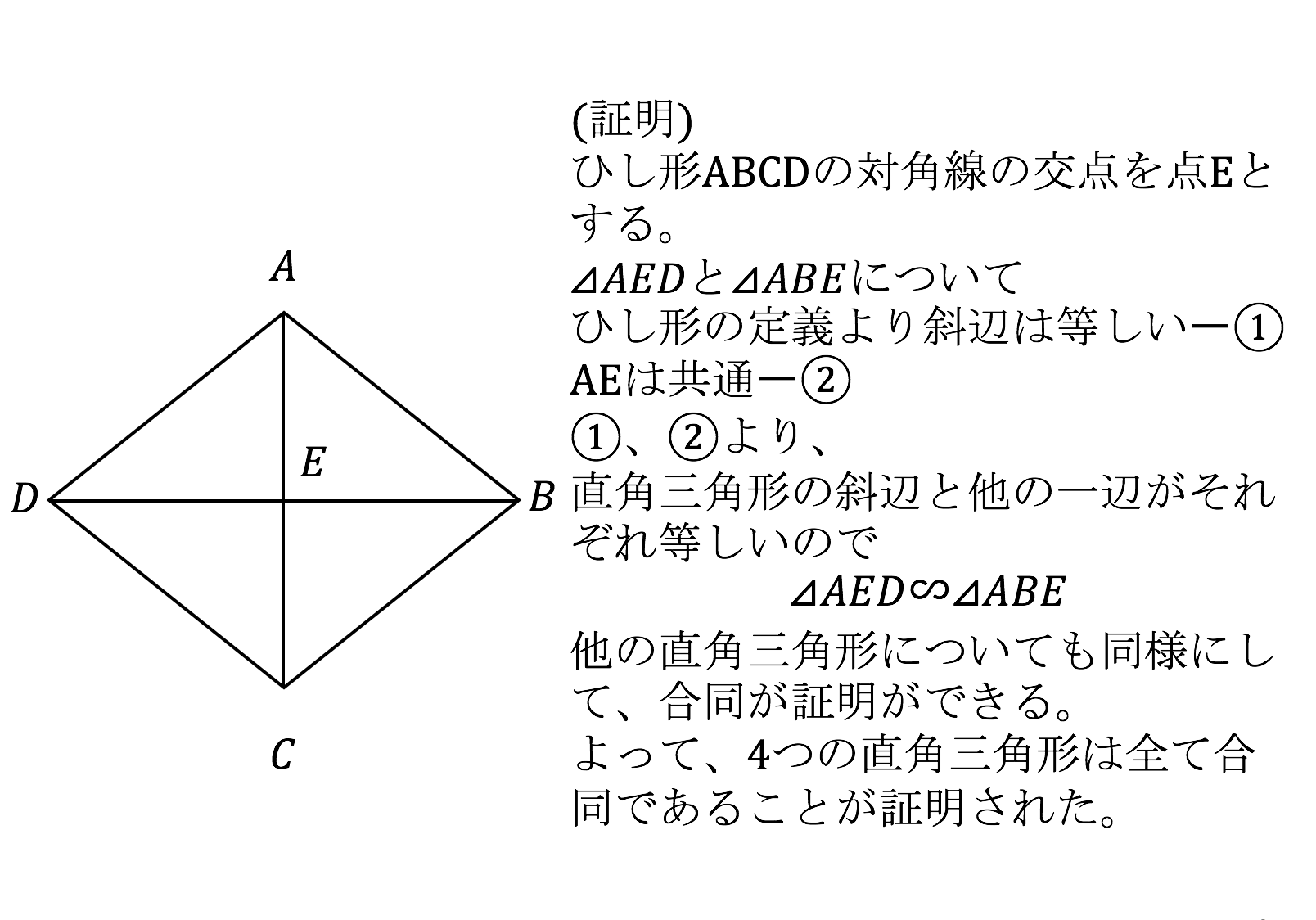
3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ

中点連結定理を使った平行四辺形であることの証明 教遊者
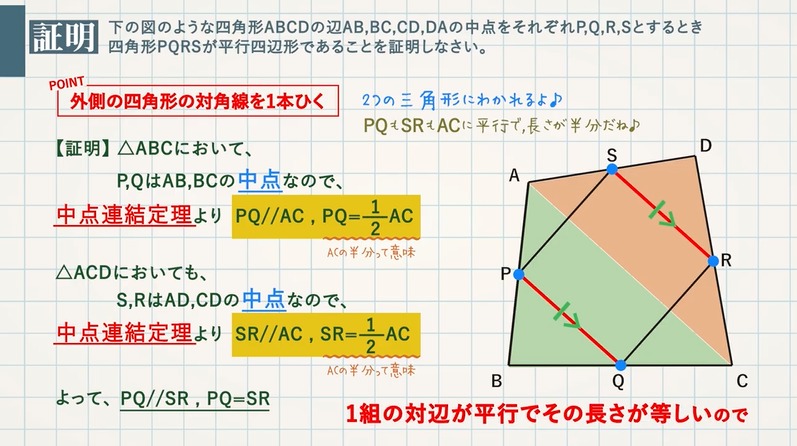
中点連結定理を使った平行四辺形であることの証明 教遊者

平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学

ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
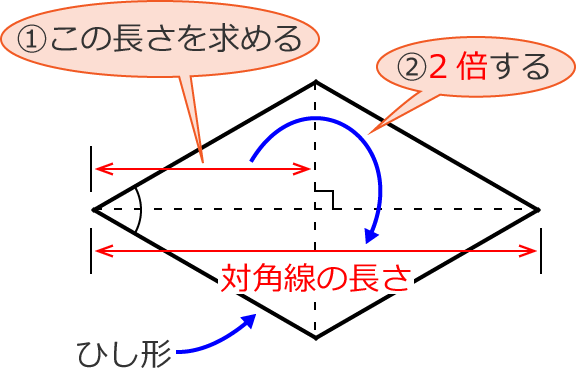
ひし形の対角線の長さの求め方
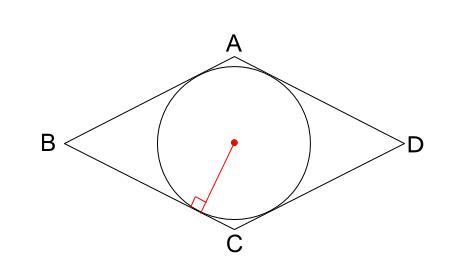
作図 ひし形の内接円 中学数学の無料オンライン学習サイトchu Su
Ed City Daito Osaka Jp

ひし形の面積の求め方 公式と計算例
Logos Jp Net

ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
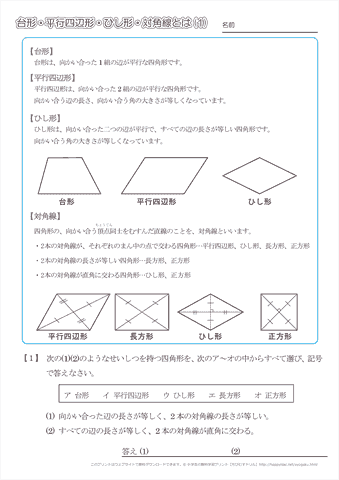
小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
Ed City Daito Osaka Jp

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
Edu City Misato Lg Jp

3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく

中3 中点連結定理の証明です やり方も教えてください Clearnote
1
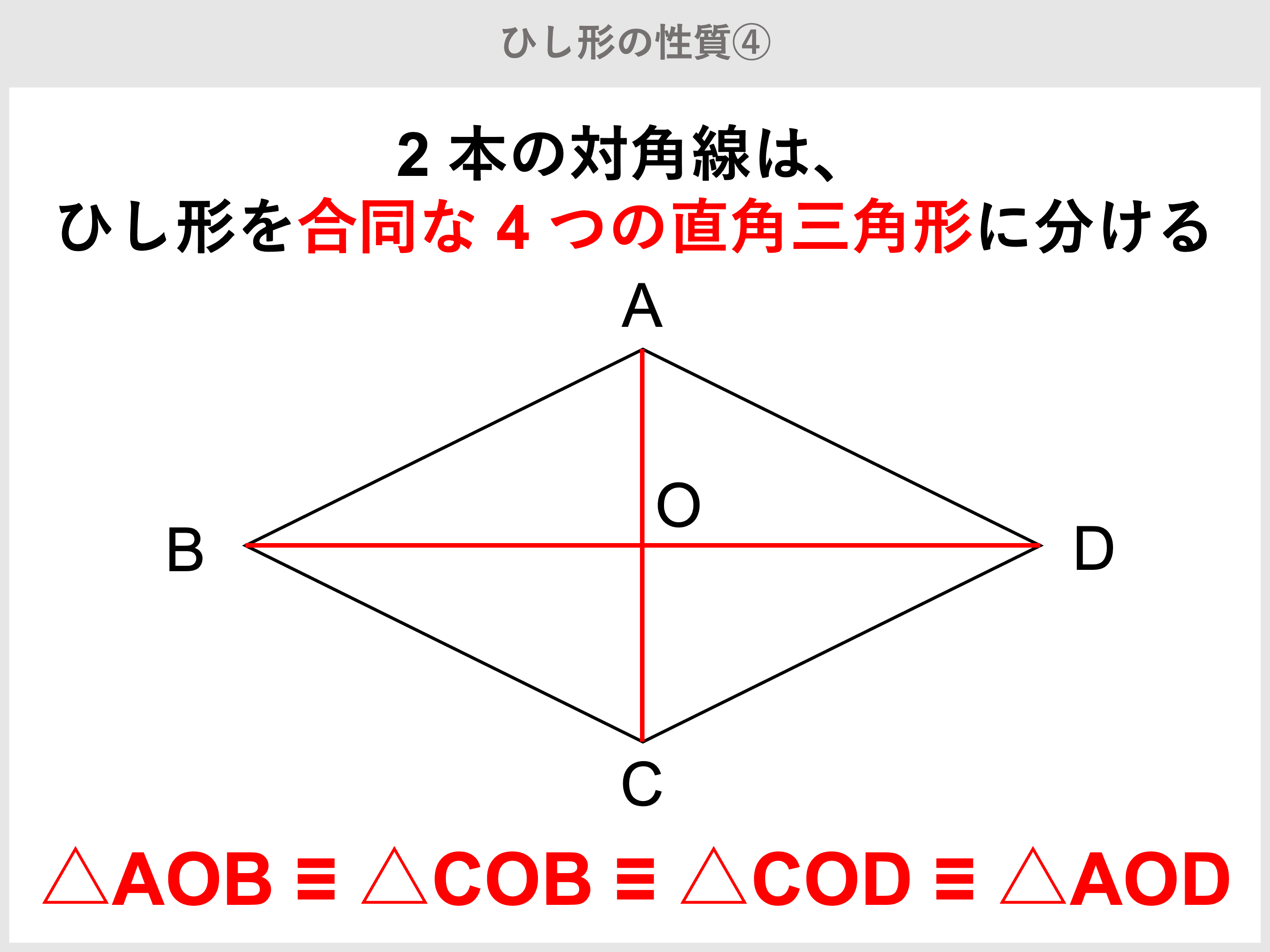
ひし形とは 定義や面積の公式と求め方 計算問題 受験辞典
ひし形とは 定義や面積の公式と求め方 計算問題 受験辞典
Edu C Pref Miyagi Jp

高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
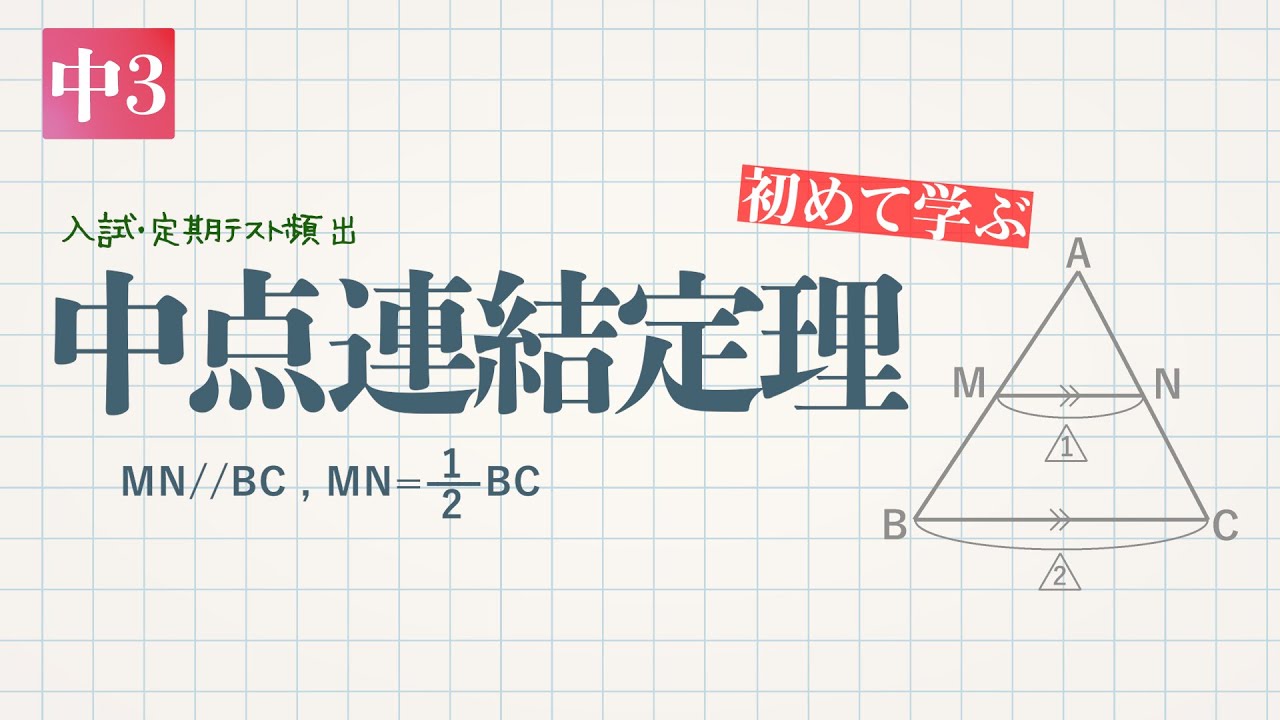
中点連結定理を使った平行四辺形であることの証明 教遊者
Tsumugi Ne Jp

ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ
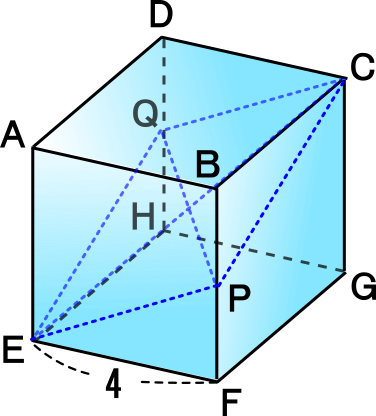
中学3年数学練習問題 三平方の定理 空間図形への利用 2
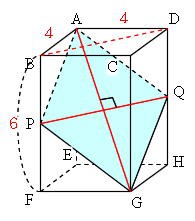
Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ

ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく

四角形の4つの辺の中点を結んでできる四角形

3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく

3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
ひし形の対角線の長さの求め方
500枚 四角形abcdのそれぞれの辺の中点 Yahoo 知恵袋

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
3

中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またそ Clearnote
正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
2 の答えがひし形になることを中点連結定理を用いて証明したいのですが 模範 Yahoo 知恵袋

中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またそ Clearnote

中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またそ Clearnote
中三数学 三平方の定理のところです B 45 一辺が4cmのひし形 Yahoo 知恵袋

証明 1 教えてください 中点連結定理使うのはわかるのですが Clearnote
3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ
ひし形の面積の公式 算数の公式

中3数学 中点連結定理ってどんな定理 まなビタミン
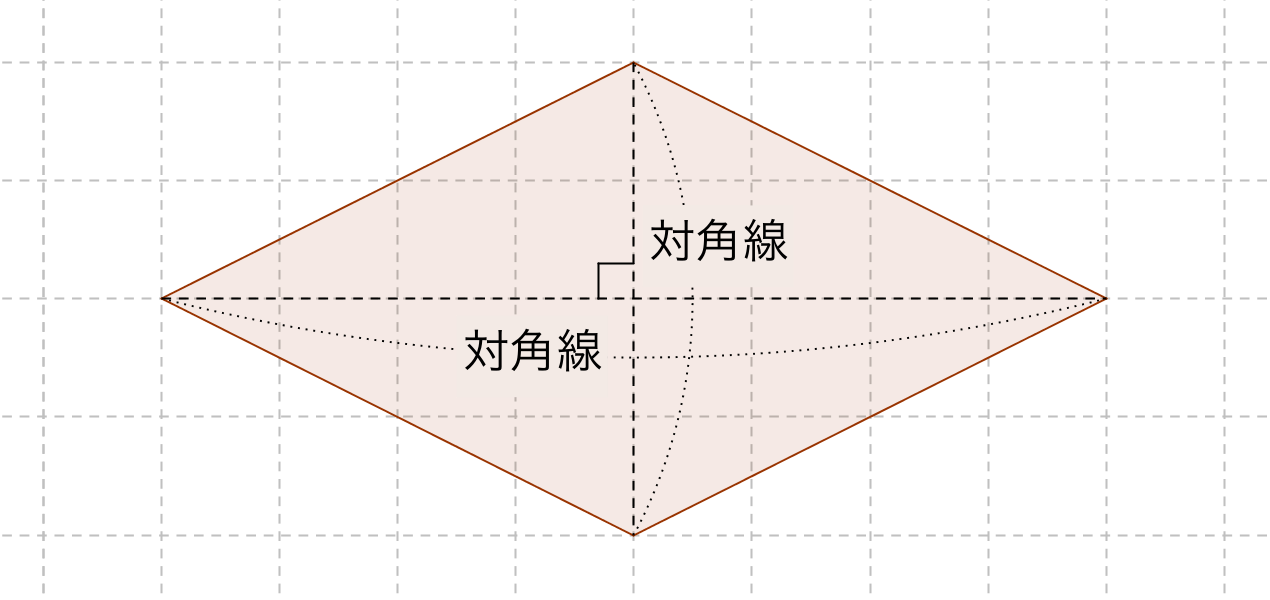
ひし形の面積の公式 算数の公式

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
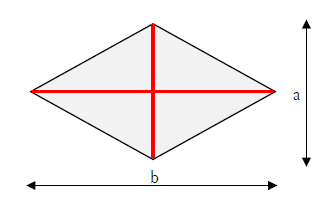
ひし形の面積は 1分でわかる求め方 公式 辺の長さ 対角線との関係

高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
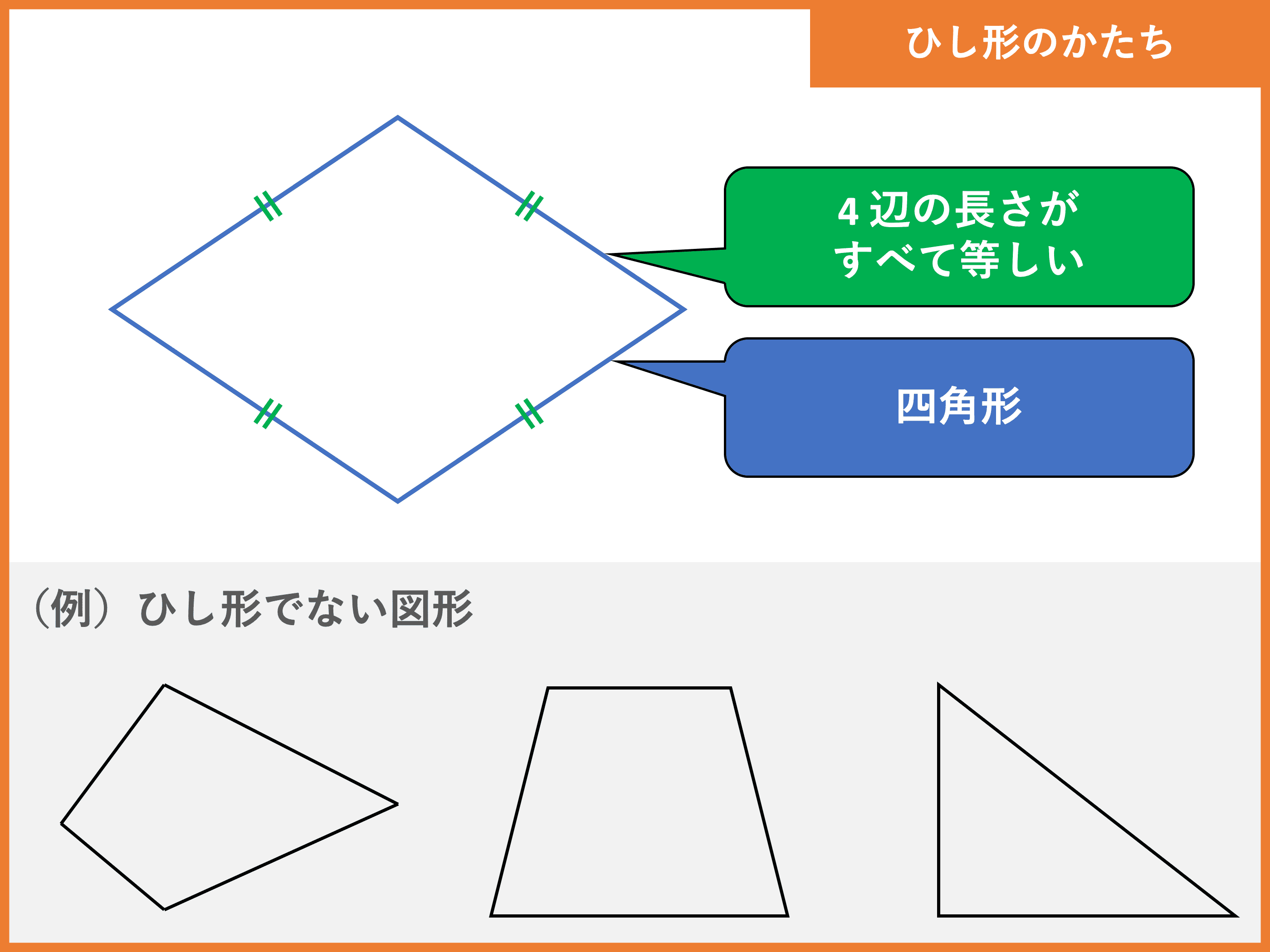
ひし形とは 定義や面積の公式と求め方 計算問題 受験辞典
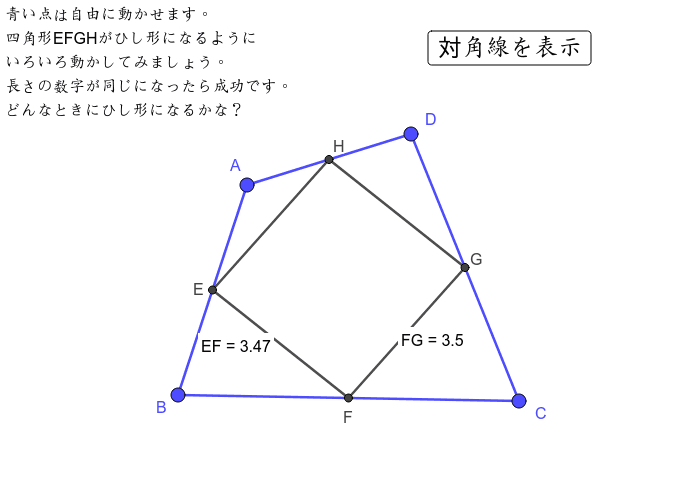
四角形abcdの各辺の中点を結んでひし形を作ろう Geogebra
ねこ騙し数学
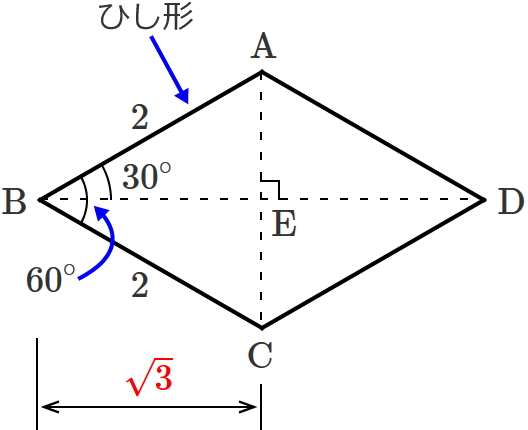
ひし形の対角線の長さの求め方

ひし形の面積の求め方 公式と計算例
菱形と長方形はどちらが美しいですか Quora
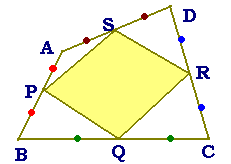
中点連結定理
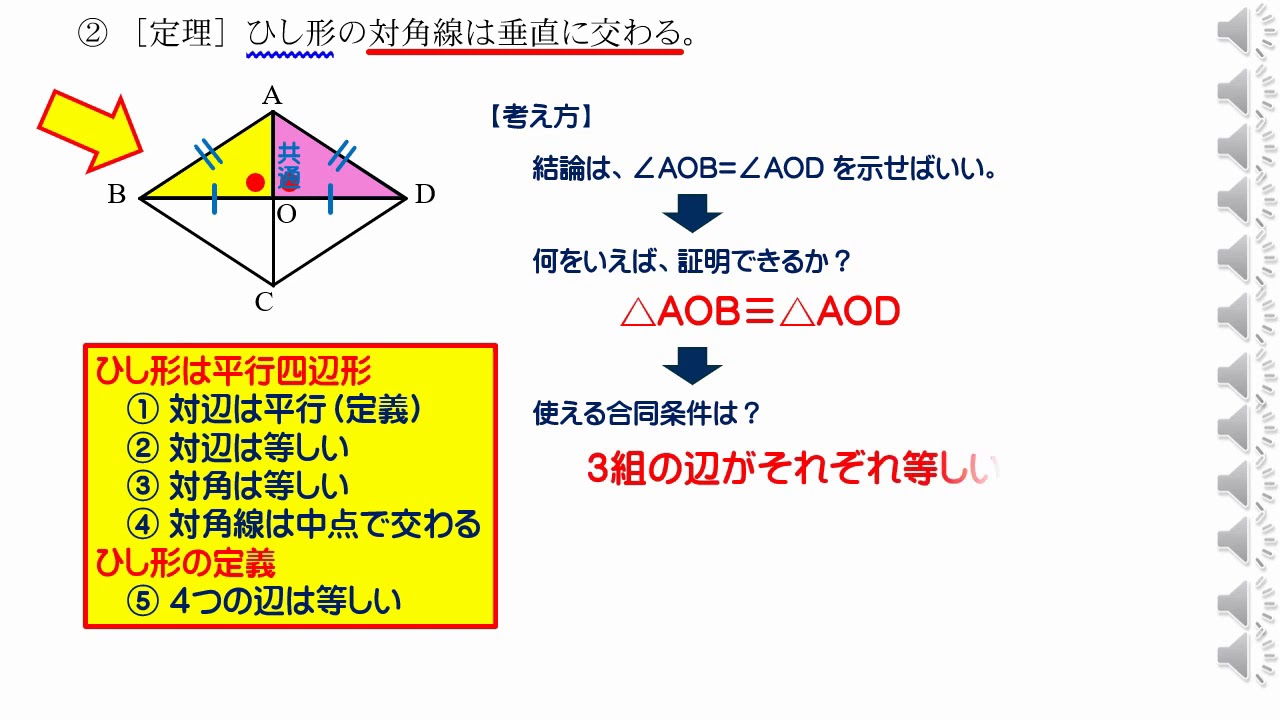
特別な平行四辺形 Youtube

ひし形の面積の求め方 公式と計算例




