中学 数学 中央 値
中3数学「真の値と近似値の定期テスト過去問分析問題」 近似値・誤差の練習問題です。 最近少しずつ入試でも出題され始めたところであります。 練習を重ねて習得していきましょう。 近似値・誤差 近似値と誤差真の値に近い値を近似値、近似値と.
中学 数学 中央 値. 単元 資料の分析,資料の活用,近似値と有効数字, 「中1の7章をまとめました! 度数分布表や代表値などが書かれています。 いいね、フォローよろしくお願いします🙇♂️」, 学年 中学1年生, キーワード 中1,数学,度数分布表,ヒストグラム,柱状グラフ,相対度数,ラマ,代表値,平均値,中央値. 中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく. 中央値は 真ん中の人の値 だったよね。 データは全部で 12個 あるから、「6番目の人の値」と「7番目の人の値」の平均値が中央値になるね。 xがないときには、中央値は8 では、xを除いて、 値の大きい方から並べて 考えてみよう。 xがないときには、中央値は8になっている ね。 このデータの中に、xが8以上の値としてはいってくるか、8より小さい値になるかで中央値は変わってくるんだ。 xが8以.
入試日 02/04 80偏差値 59 50偏差値 55 中央大学附属中学校の偏差値です。 80偏差値:合格可能性80%に必要な偏差値です (併願校を選定する際にご利用ください)。 50偏差値:合格可能性50%に必要な偏差値です (第一志望校を選定する際にご利用ください)。. 小学算数では以前よりグラフが難しくなり、代表値も扱うようになります。速さは小5、分数×整数、分数÷整数は小6で初めて学習するように。 中学数学では従来中1で扱っていた誤差、近似値、a×10 n が、中3で学習することになります。. 中学数学中央値の求め方をイチから解説するぞ! kaztaro 中学数学・理科の学習まとめサイト! 資料の活用 中学数学最頻値の求め方をイチから解説するぞ!.
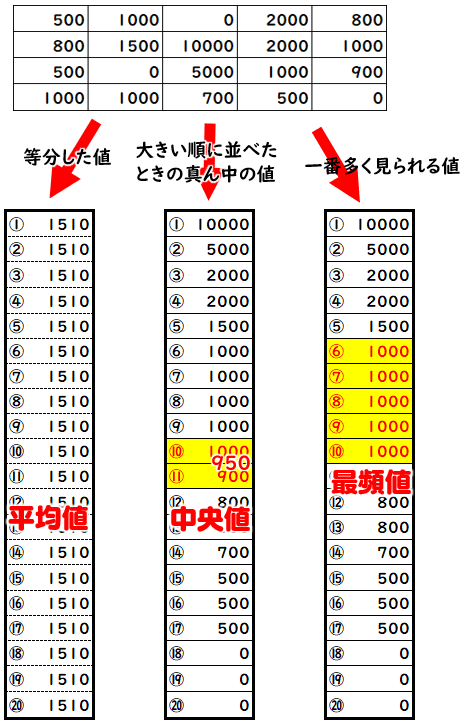
代表値とは、データ全体の特徴を表した値のことです。 平均値 は、「すべての数値を足して、数値の個数で割ったもの」、 中央値 は、「数値を小さい方から並べたときに、真ん中に来るもの」、 最頻値 は、「一番個数が多いもの」です。 どれも「データを特徴づける値」ですが、 それぞれの代表値には、得意・不得意があります 。 データが次のようにきれいな左右対称の山の形に. 中央値(メジアン) 資料の値を大きさの順に並べた時の中央の値を 中央値(メジアン) という。 例 生徒25人の身長の中央値は低い方から13番目の人の値となる(高い方から数えても13番目で同じ)。 生徒数が24人の場合、12番めと13番目の2人の値の平均となる。. 中学数学をやり直したい社会人にもおすすめです。 それぞれのxの値を求めよ。ただし、点Oは円の中心である。 すると, 5つの連続する偶数は、nを整数として,中央の偶数が2nとする.
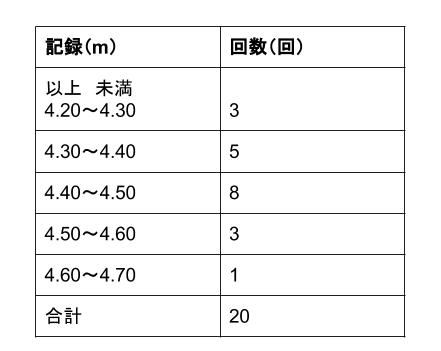
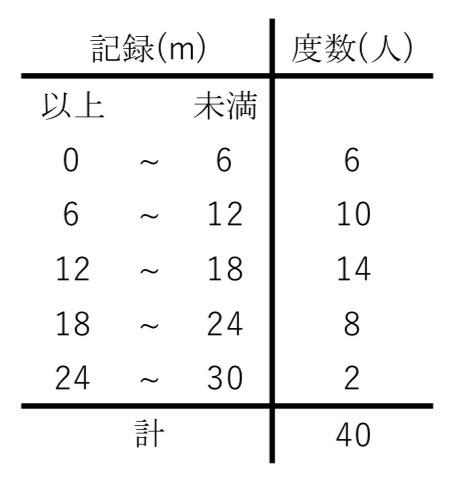
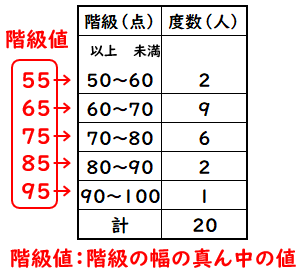
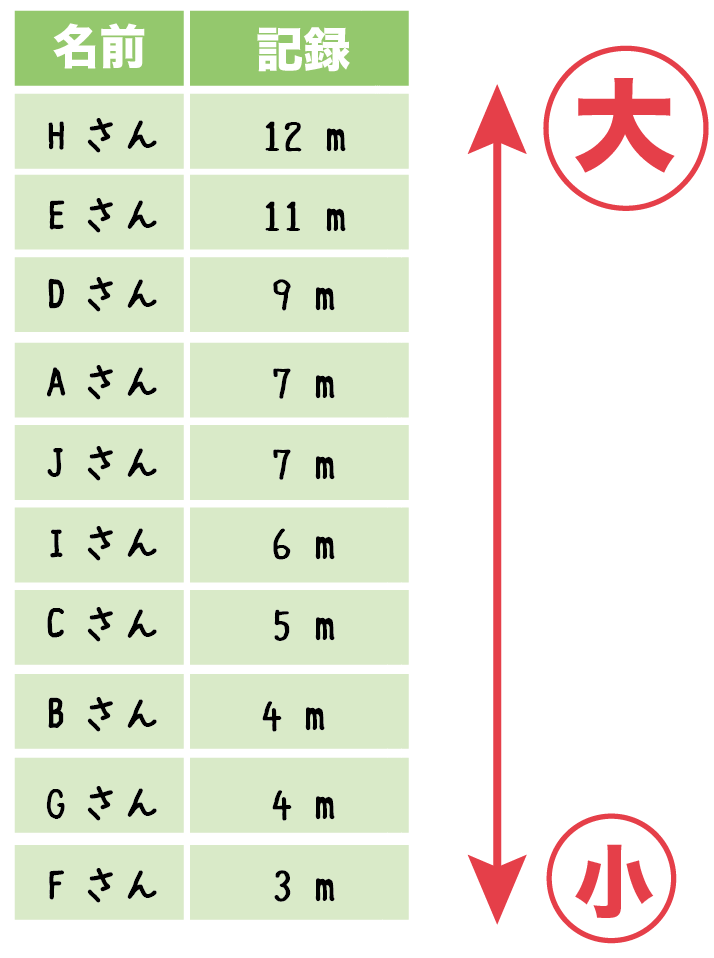
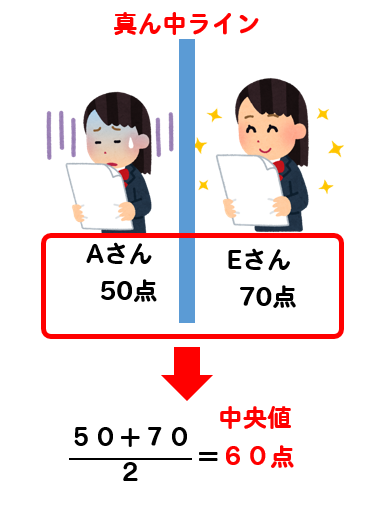
中学数学最頻値(モード)の求め方がわかる2ステップ Ken 最頻値(モード)の求め方がわからない!. であり、真ん中の値は 159 159 と 156 156 です。 この 2 2 つの平均が、偶数個の資料の中央値です。 ()÷2 = 1575 ( 159 156) ÷ 2 = 1575 よって、求める中央値は 1575(cm) 1575 ( c m) です。 度数分布表からの中央値 度数分布表からは、各資料の真の値はわかりません。 よって、階級値を用います。 例1 表は、 A A さんの走り幅跳び 回の記録である。 中央値を求めなさい。 解説. 中央大学附属中学(小金井市)の偏差値・口コミなど、学校の詳細情報をまとめたページです。他では見られない情報が満載です。 数学と英語は補修がたまにあります。 東京都の中学の偏差値の一覧を一目で見ることができます!.
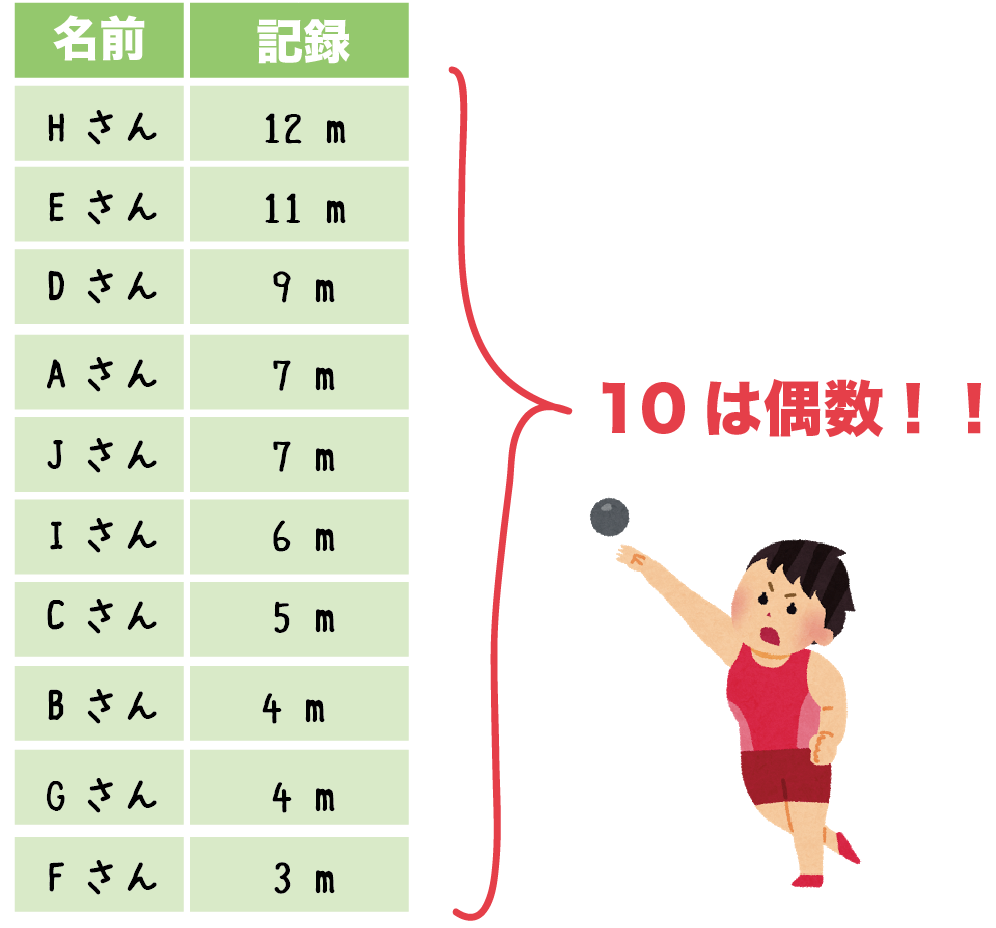
中央値(奇数個のとき)の練習問題解答 記録を順にならべると、 68、69、70、79、、、となり真ん中にくるのが、79となります。 よって中央値は、79です。 中央値(偶数個のとき)の練習問題 次のような、あるクラスのグループ8人の10点満点の小テストの記録です。 8人の記録の中央値を求めてみましょう。 中央値(偶数個のとき)の練習問題解答 記録を順にならべると、 6. ~ 中学1年 数学 ~ Lesson 47 代表値-平均値・階級値・中央値・最頻値 第7章 資料の活用 <<L46 度数分布・ヒストグラム・相対度数 の問題に戻る L47 代表値平均値・階級値 の解答表示>>. 「中央値」の特徴と求め方 中央値は 大きい順に並べたときの真ん中に位置するデータの値 です。 データの数が奇数個ならちょうど真ん中のデータが存在するのですが、偶数個の場合は2つのデータにまたがった位置が真ん中となってしまいます。 たとえばデータが21個なら11番目に大きい値が中央値です。 しかし今回の例はデータが個なので、10番目と11番目の間がちょうど真ん中になります。.
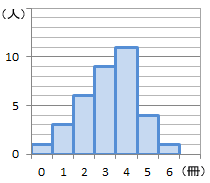
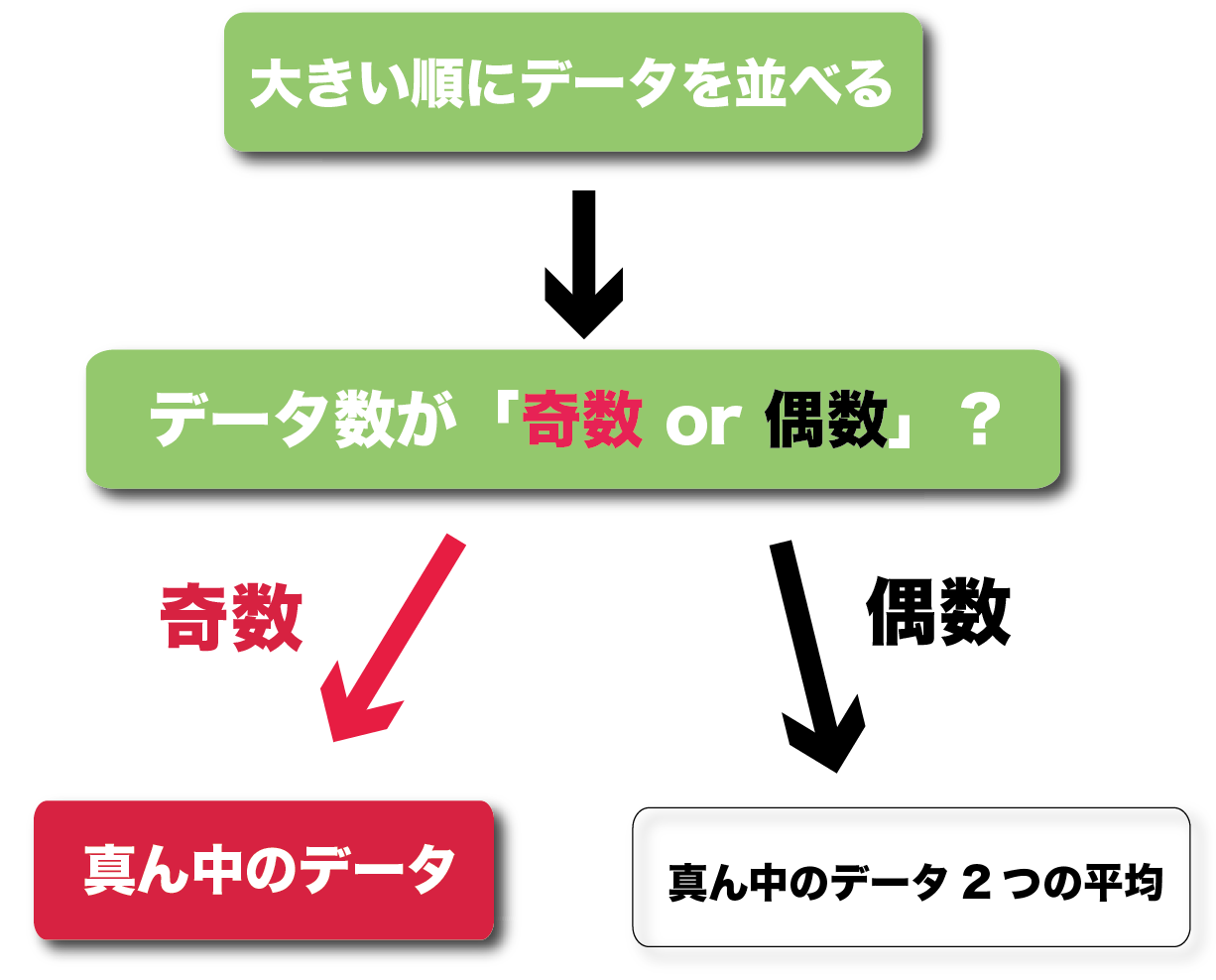
中央の順位は、 ( 1 6 )/2=35 (番目)から、 3番目と4番目の冊数の平均が中央値になります。 中央値= ( 1 2 )/2=15 (冊) 中央が何番目かを計算する方法は、中点の座標計算と同じです。 点Aの座標が (1,0)、点Bの座標が (6,0)のとき、 線分ABの中点の x 座標は、 (16)/2=35 例題1 データが5個あります。 中央値を求めてください。 (15)/2=3 から、3番目が中央値なので、 (答) 13 例題2 データ. データの大きさが 奇数 のとき、 中央の位置にくる値をそのまま中央値 とします。たとえば、データの大きさが5個であれば、3番目の値が中央値になります。 それに対して、データの大きさが 偶数 のとき、 中央の2つの値の平均値を中央値 とします. 代表値 定義 代表値:資料全体の特徴を1つの数値で代表させたもの 例) 平均値,中央値,,最頻値 階級値:階級の中央の値 ※度数分布表から平均値を求めるときには,ある階級に入っている全ての資料は階級値をとるとみなして計算する。.
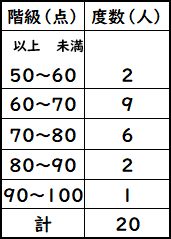
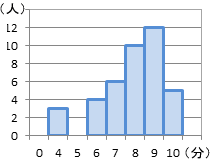
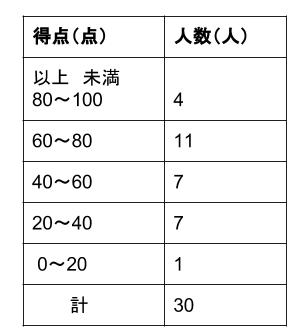
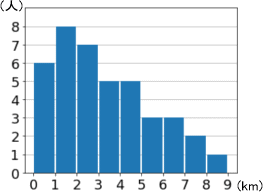
代表値 資料の特徴を表す値を代表値といいます。 平均値、最頻値、中央値 などがあります。 このページでは、「最頻値」について学習しましょう。 最頻値 最頻値は、資料の中でもっとも多くあらわれる値のことで、モードともいいま. 中学数学高校入試で使える重要公式を一覧でまとめ 三乗の展開公式(ab)3乗の計算方法は?問題 時間・分・秒を変換計算式はどうやる? 中央値 最頻値 平均値 相対度数 など. 中央値は、5番目と6番目の中央の値なので、 (2324)/2=235 (m) ・・・ (答) 2 (1) 度数合計が70なので、 ア=70 () =7062=8 ・・・ (答) (2) (170)/2=355 から、 中央値は、35番目と36番目の中央の値になる。 度数の累計から、 35番目と36番目が含まれる階級は、1 ~ 150 (答) 1分以上150分未満 3 Gの点数、Hの点数をG、Hとする。 条件から、 G>H ・・・① 平均値.
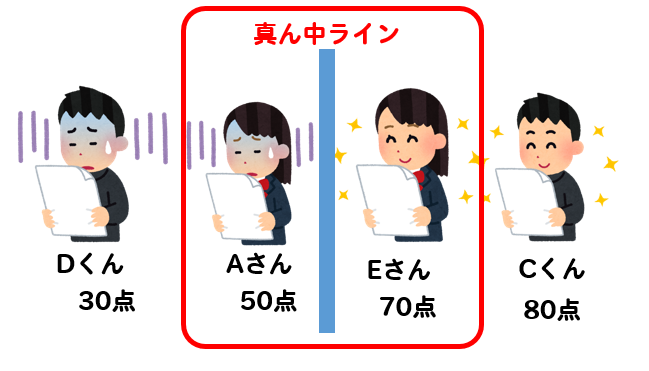
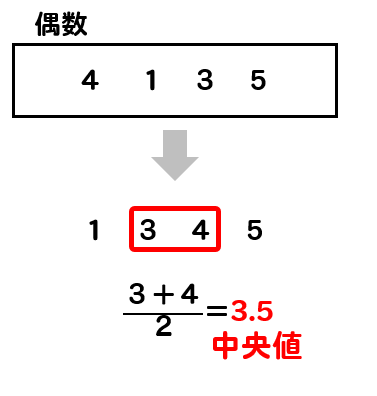
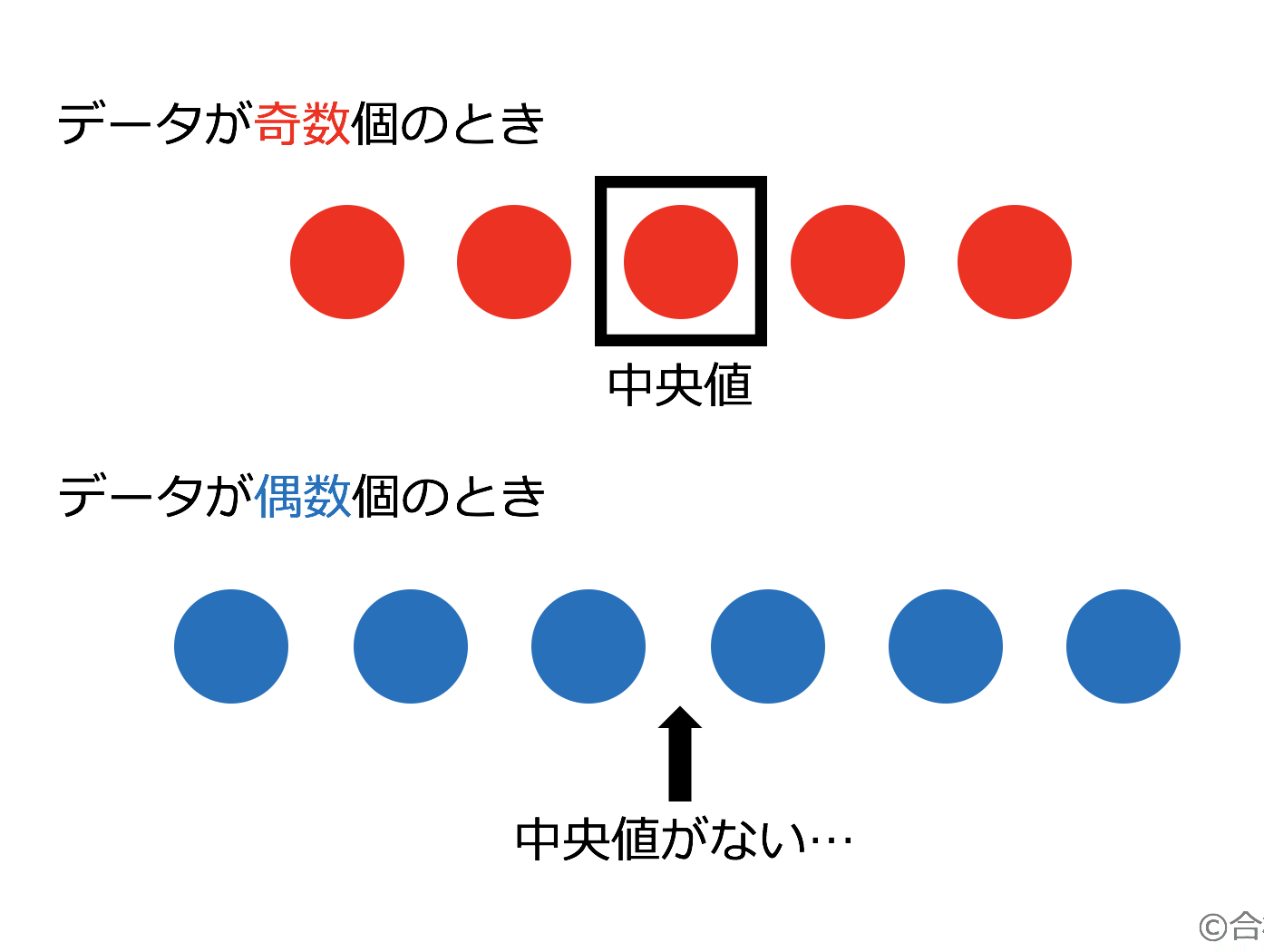
1 男女それぞれの中央値(メジアン)を求めなさい。 ≪小さい順に並び替える≫ 男子 ⇒ 39、40、43、44、45、48、52 女子 ⇒ 35、37、38、40、41、42、43、45 ≪女子の中央値の計算≫ (40+41)÷2=40.5 ≪答≫ 男子の中央値:44kg、 女子の中央値: 40.5kg 2 男女それぞれの平均値を小数第二位まで求めなさい。 男子 ⇒ (39+40+43+44+45+48+52)÷7=44.428. 中央値とは、 「データを大きい順(または小さい順)に並べたとき、真ん中に来る値」 のことを言います。 中央値は メジアン と呼ばれたりもします。 真ん中の値を図で確認してみましょう。 データの数が奇数個のときは真ん中の値がちゃんと出てきましたが、偶数個のときは真ん中がありません。 偶数個のときはどうするのでしょうか? データの数が偶数個のときは真ん中の2つ. 度数分布とは? 表や多角形の作り方、平均値・中央値・最頻値の問題 21年2月19日 この記事では、「度数分布」についてわかりやすく解説していきます。 度数分布表や度数分布多角形の作り方、平均値・中央値・最頻値を問う問題も説明していくので.
中学2年生の最初に追加されたのがこの2つです。 今までは高校生の数学Ⅰにあったもので、中学数学に存在しませんでした。 中央値が使われており、中学1年生の統計の内容の延長です。 簡単なのですがうっかり勉強しそびれそうな、存在の薄い単元です。. 中央値とは、データを小さい順、または大きい順に並べたとき、 中央の順番に位置する『値』 です。 例えば、 つのデータ があるとき、小さい順並べ直し、 真ん中の 番目にある が中央値になります。 データの最小値と最大値の中間(順番的に)にある値になるので、 最小値付近や最大値付近より中央よりの方が似たような値が多い ということから使われる代表値です。 中央値を求めるときの注意点. 平均値以外の代表値として、中央値 正の数と負の数 22 文字と式(中学) 19 一次方程式 23 比例と反比例(中学) 16 平面図形(中学) 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数.
1
中央値 求め方
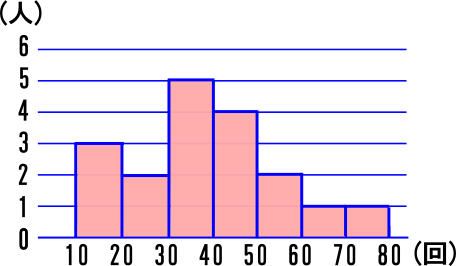
中学1年数学練習問題 平均値 階級値 中央値 最頻値の求め方と解答
中学 数学 中央 値 のギャラリー

資料の活用 中1数学 中3総合a対策 しおちゃんの元氣アップ ココロのサプリ

中1数学 資料の活用 中央値 資料の総数が偶数の場合 Youtube

中央値 最頻値 中1数学 資料の活用4 Youtube

中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中一 数学 代表値 中学生 数学のノート Clearnote

中学数学 資料の散らばりと代表値

数学 代表値 中学生 数学のノート Clearnote
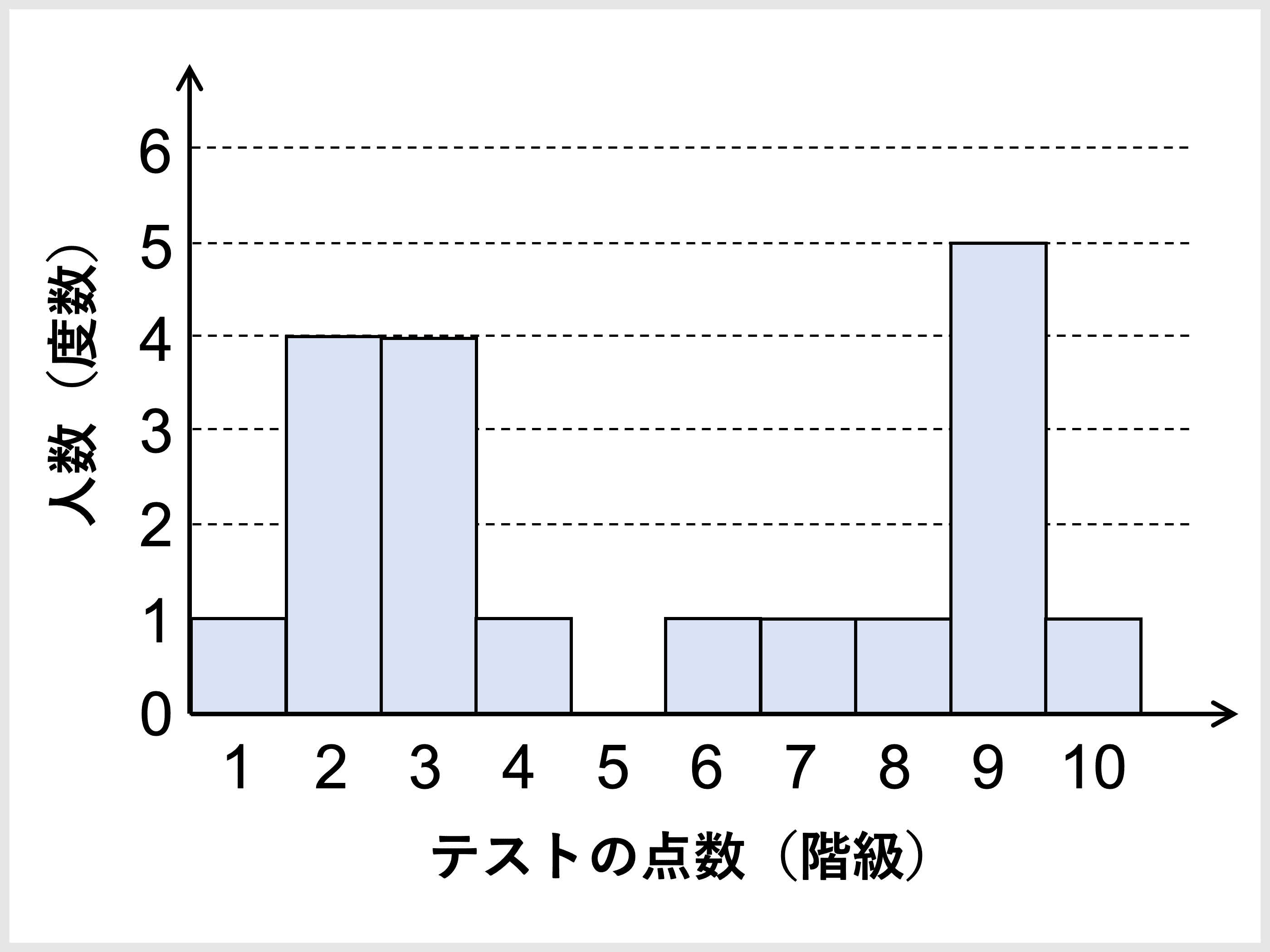
平均値 中央値 最頻値の違い 求め方 使い分け 計算問題 受験辞典
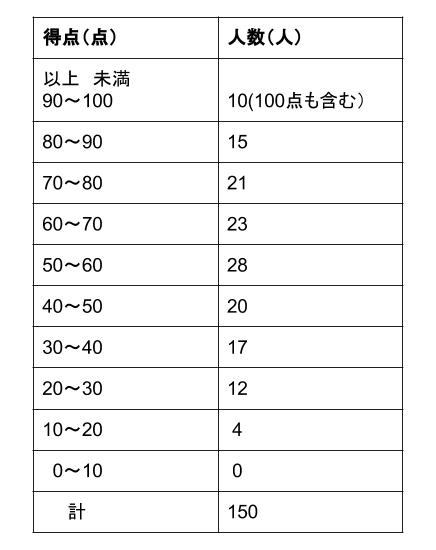
中学数学 度数分布表 ヒストグラム 中学数学の無料オンライン学習サイトchu Su
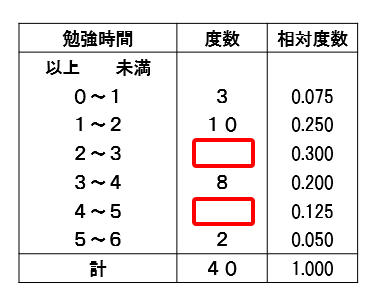
中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
代表値 平均値 中央値 最頻値 の意味と違い 数学fun

代表値の応用問題 教遊者

中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく
中央値を求める2 中学から数学だいすき
平均値 最頻値 中央値の求め方 あるクラスの男子生徒20人の Yahoo 知恵袋
中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋
3つの代表値 中学から数学だいすき

中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
Pref Hiroshima Lg Jp

代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 教遊者

中1数学 資料の散らばりと代表値 まとめ 中学生 数学のノート Clearnote

中1数学 相対度数と代表値のポイント Examee

平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ

度数分布表から平均値を求める 中学1年の数学 身勝手な主張
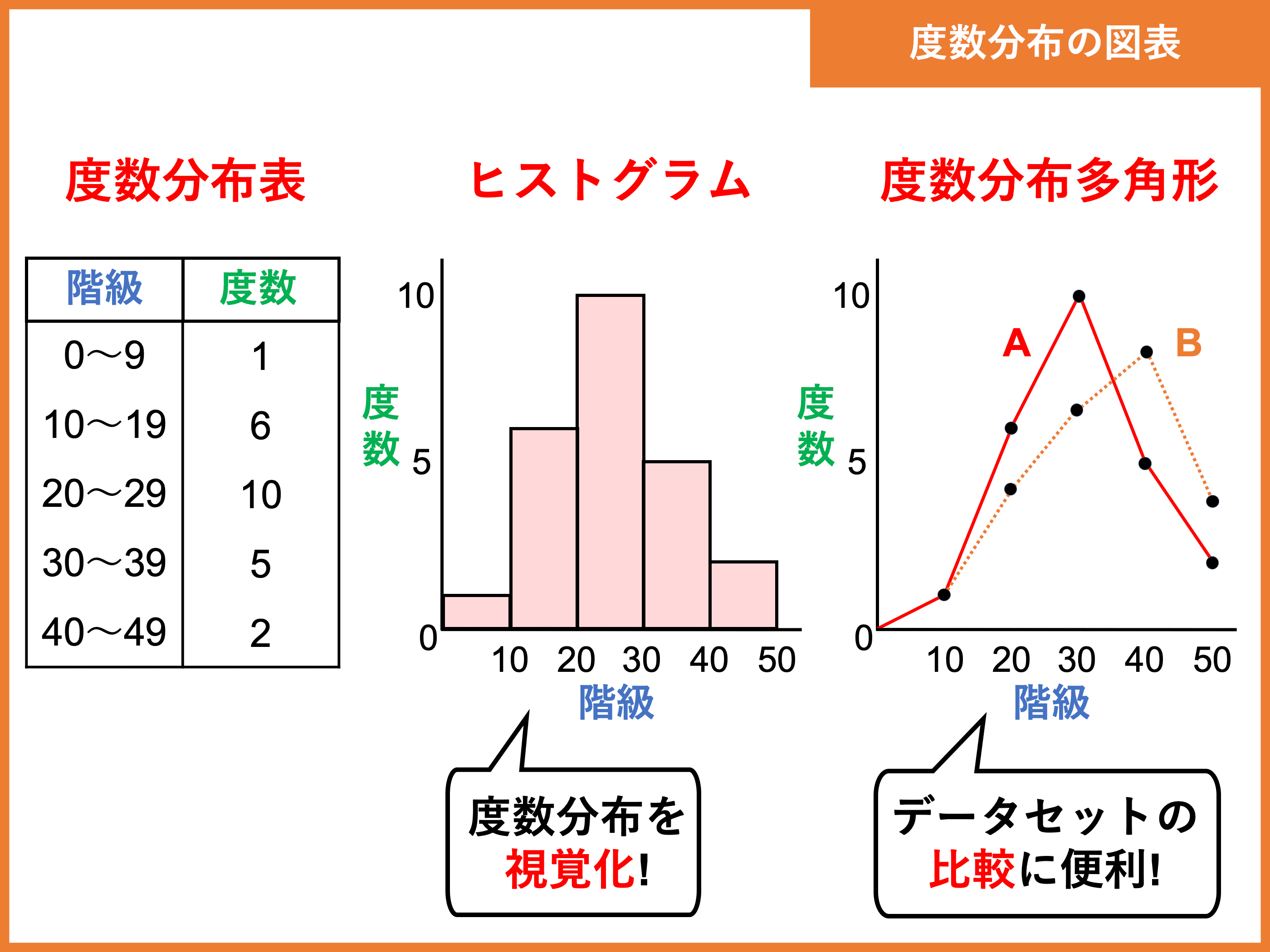
度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典
代表値 平均値 中央値 最頻値 の意味と違い 数学fun
これの中央値 最頻値 平均値の求め方を教えてください 中央値とは言 Yahoo 知恵袋
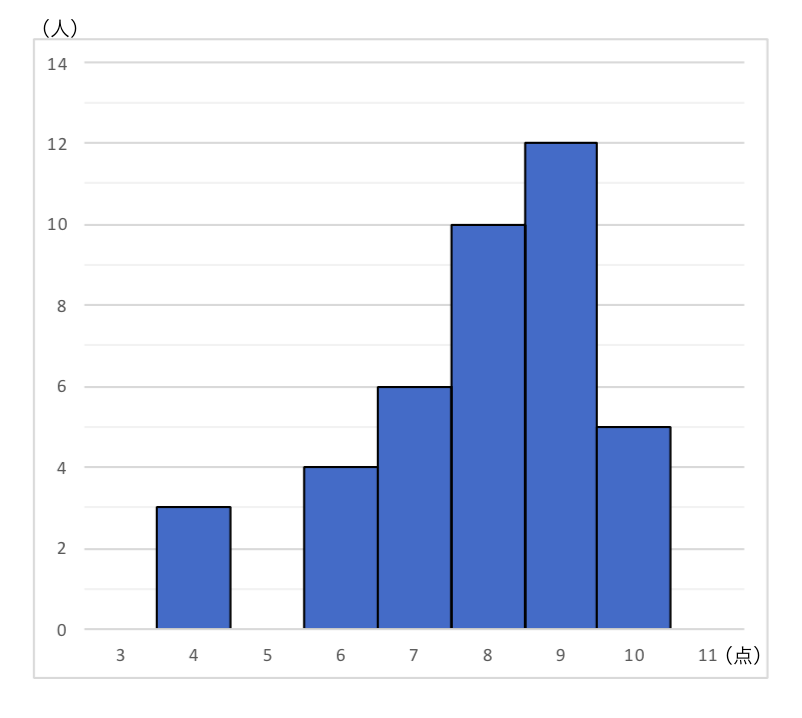
ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に

度数分布表からの平均値の求め方 中学数学 定期テスト対策 ベネッセ教育情報サイト
中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ

中1 数学 中1 87 代表値と散らばり Youtube
中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su

算数 中学数学 数 算数でも数学でも出てくる 平均値と中央値 の違い 年収のお話もあるよ 年度学習指導要領改訂で中央値は算数で習うようになりました Youtube

十王はなまる塾 7 17 教科書が新しくなって 小6算数 今年から教科書が新しくなりました 小学6年算数 資料の整 理 というところに 代表値としての平均値 中央値 最頻値 ドットプロット などが新しく学習する内容として入りました これはこれまで
度数分布表から平均値と最頻値を求める 苦手な数学を簡単に

中学校数学1年 資料の活用 代表値と散らばり 最頻値まで Youtube

中学校数学映像講座 統計 中央値と平均値 ふるやまんの算数塾

中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく
中央値を求める 中学から数学だいすき

数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ
中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 中央値 メジアン を求める意味って Qikeru 学びを楽しくわかりやすく

中1 資料の活用 代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 デジタル板書データ リクエスト動画 Youtube

代表値 平均値 中央値 最頻値 の意味と違い 数学fun

高校数学 代表値 平均値と仮平均法 受験の月

中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ

中1 中1 数学 範囲 代表値 大放出ぅ 中学生 数学のノート Clearnote
代表値 平均値 中央値 最頻値 の意味と違い 数学fun

中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 教遊者
中央値を求める 中学から数学だいすき
中1数学中央値についてあるサイトで中央値の求め方は 1 データ数 Yahoo 知恵袋

代表値 平均値 中央値 最頻値 の意味と違い 数学fun

中学数学 資料の散らばりと代表値
中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
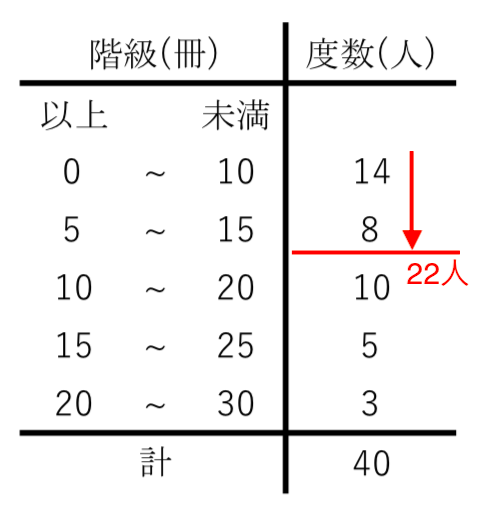
度数分布表から相対度数を求める 苦手な数学を簡単に

3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ
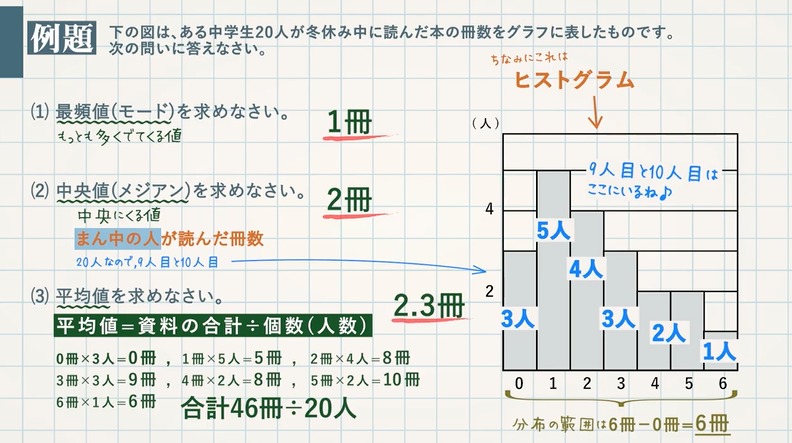
代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 教遊者

中学1年の数学 動画 代表値と散らばりの問題 19ch

5分で分かる 中学数学 116 中央値 範囲 Youtube
3

中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく
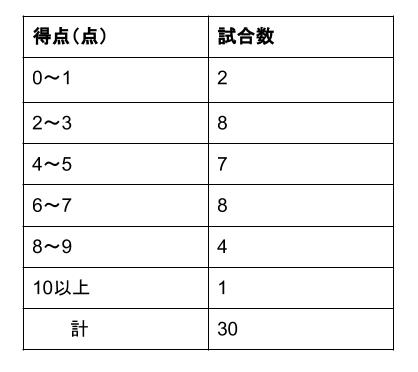
中学数学 代表値 最頻値 中学数学の無料オンライン学習サイトchu Su
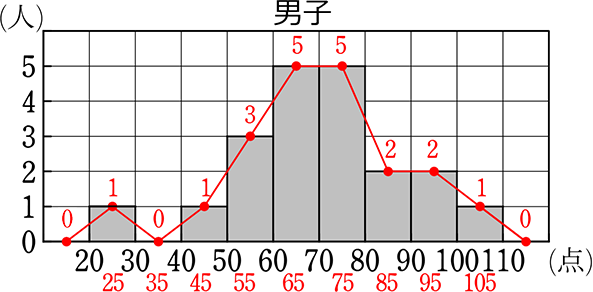
中学数学 資料の散らばりと代表値

メジアン と モード 中学数学 資料の活用 をファッションでおぼえる 愛知県安城市の個別塾 学習塾 ナビ個別指導学院 安城南校ブログ

世界一わかりやすい数学問題集中1 7章 資料の活用
資料の分析 代表値の関係 中学から数学だいすき

平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ

中1 数学 7 3 中央値 最頻値 Youtube

中央値について 真ん中の落とし穴に気をつけろ 苦手な数学を簡単に

中1数学 相対度数 平均値 最頻値 近似値 中学生 数学のノート Clearnote

中学数学 きょうの1題 資料の散らばり 11 中学数学高校数学個別指導in山形市 数専ゼミ

平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ

平成25年長野県立高校 入試問題 平均値 中央値 最頻値の問題 現役塾講師のわかりやすい中学数学の解き方

中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット
City Funabashi Lg Jp
中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

平均値 中央値 最頻値はどう使い分ける 3つの代表値を詳しく解説 遊ぶ数学

中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ

代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 教遊者

高校数学 代表値 中央値 メジアン と最頻値 モード 受験の月

中央値の簡単な求め方みたいなのがあったら教えて頂きたいです Clearnote

中学数学資料活用 の新着タグ記事一覧 Note つくる つながる とどける
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ

中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ
3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ

高校数学 中央値 と 最頻値 練習編 映像授業のtry It トライイット
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ
3

中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット
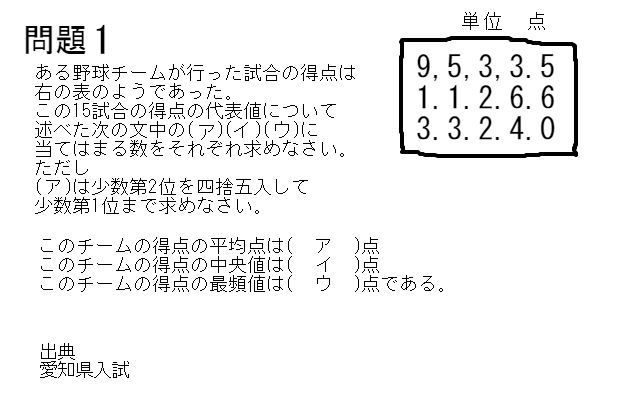
得点源 平均値 中央値 度数分布表 まとめ 中学 数学 理科の復習サイト

中学数学 3つの代表値の求め方 Qikeru 学びを楽しくわかりやすく

中学数学 中央値の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中1資料の活用 中学生 数学のノート Clearnote

数理統計学事始 平均値と中央値をさまざまな視点でみる 数学 統計教室の和から株式会社
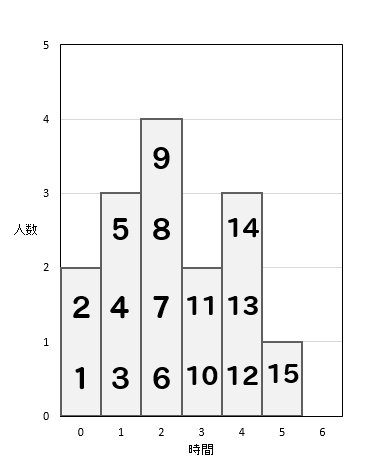
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ

世界一わかりやすい数学問題集中1 7章 資料の活用




