Let The Circle X 12+y 2225 Cuts Rectangular Hyperbola
Question 10 The circle x 2 y 2 = 8x and hyperbola x 2 /9 – y 2 /4 = 1 intersect at the points A and B Find the equation of a common tangent with positive slope to the circle as well as to the hyperbola Solution The equation of circle x 2 y 2 = 8x can be rewritten as (x – 4) 2 y 2 = 16 Tangent to hyperbola is y = mx √(9m 24.

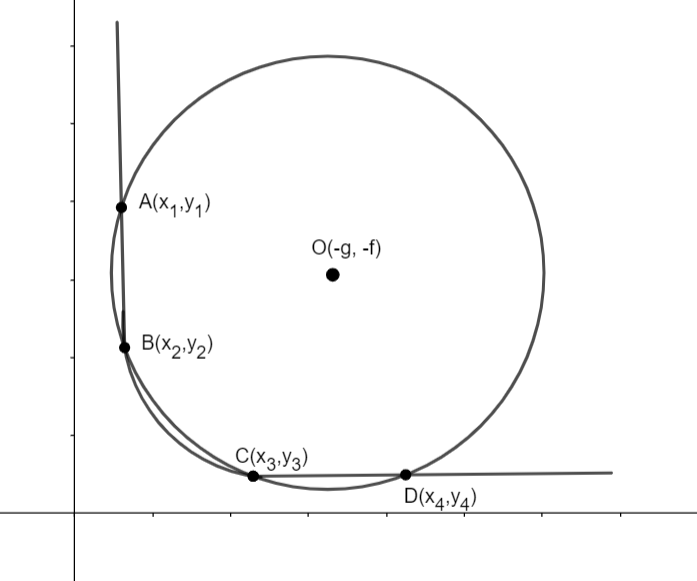
Let the circle x 12+y 2225 cuts rectangular hyperbola. 2 Each slice will be roughly rectangular in shape, with height yand width x From similar triangles, the height yfor a slice a position xwill satisfy y 3 = x 6 or y= x 2 1 Thus the area of one rectangular slice will be width height = ( x) x 2 = x 2 ( x) Since the slices begin at x= 0 and end at x= 6, Total area = Z 6 0 x 2 dx = x2 4 6 0 = 36 4 0 = 9 sq units Check Area of a triangle = 1 2. A rectangular hyperbola and a circle meet in four points The mean of these four points is the middle point of the centres of the hyperbola and that of the circle Let us explain this concept in detail Let the rectangular hyperbola be xy = c 2 and the equation of the circle be x 2 y 2 2gcp 2fy k = 0 Any point on the hyperbola is (cp. Where S is the hemisphere given by x2 y2 z2 = 1 with z ≥ 0 Solution We first find ∂z ∂x etc These terms arise because dS = q 1(∂z ∂x) 2 (∂y) 2dxdy Since this change of variables relates to the surface S we find these derivatives by differentiating both sides of the surface x2 y2 z2 = 1 with respect to x, giving 2x2z∂.
The angle between the asymptotes of is 2 tan1 (b/a) or 2 sec1 (e) Director Circle The locus of the point of intersection of the tangents to the hyperbolo , which are perpendicular to each other, is called a director circle The equation of director circle is x 2 y 2 = a 2 – b 2 Rectangular Hyperbola A hyperbola whose asymptotes include a right angle is said to I. Examples Based on Hyperbola Illustration 1 If the chords of the hyperbola x 2 – y 2 = a 2 touch the parabola y 2 = 4ax, then the locus of the middle points of these chords is the curve (a) y 2 (x a) = x 3 (b) y 2 (x – a) = x 3 (c) y 2 (x 2a) = 3x 3 (d) y 2 (x – 2a) = 2x 3 Solution Let the midpoint of the chord be (h,k) Then, the equation of the chord of x 2 – y 2 = a 2 is. The circle x^{2}y^{2}=4x2y2=4 cuts the line joining the points A(1,0)A(1,0) and B(3,4)B(3,4) in two points P Get the answers you need, now!.
As we have seen, cylindrical surfaces don’t have to be circular A rectangular heating duct is a cylinder, as is a rolledup yoga mat, the crosssection of which is a spiral shape In the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a. Answer (1 of 2) Rectangular hyperbola is a hyperbola for which the asymptotes are perpendicular, also called an equilateral hyperbola or right hyperbolaThis occurs when the simajor and semiminor axes are equal So, a=b Since the eccentricity of the hyperbola is given by e=( (a^2 b^2)^(1. A circle cuts the rectangular hyperbola xy = 1, in the point (xr, yr ) r = 1, 2, 3, 4, prove that x1 x2 x3 x4 = y1 y2 y3 y4 = 1.
KVPYSX 18 Math Paper with Solutions KVPYSX 18 paper with solutions Maths is a perfect resource for those who are preparing for KVPY examination The first step towards the KVPY Exam Preparation is to solve the Previous Year Question Papers Along with the question paper, the answer key has also been provided here. Show that the ellipse $$ \frac{x^2}{a^2} \frac{y^2}{b^2} = 1 $$ and the hyperbola $$ \frac{x^2}{α^2} −\frac{y^2}{β^2} = 1 $$ will inte Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack. The parametric equations of the circle x2 y2 = r2 are given by x = r cosθ, y = r sin θ where θ is the parameter and the parametric equations of the circle (x – h)2 (y – k)2 = r2 are given by x – h = r cosθ, y – k = r sinθ or x = h r cosθ, y = k r sinθ Fig 115 NoteThe general equation of the circle involves three constants which implies that at least three conditions.
Get answer Statement 1 Every line which cuts the hyperbola x^2,4y^2,16=1 at two distinct points has slope lying in (2,2)dot Statement 2 The slope of the tangents of a hyperbola lies in (oo,2)uu(2,oo)dot. Let’s now prove that the circulation form of Green’s theorem is true when the region D is a rectangle Let D be the rectangle a, b × c, d a, b × c, d oriented counterclockwise Then, the boundary C of D consists of four piecewise smooth pieces C 1, C 1, C 2, C 2, C 3, C 3, and C 4 C 4 (Figure 634) We parameterize each side of D as follows C 1 r 1 (t) = 〈 t, c 〉, a ≤ t. (b) Z1 0 Zp x x2 p x.
B e = 2/√3;. C e = √3/2;. Answer (1 of 2) Normally multiplying an expression with i hides it from the real plane (so it is not totally lost) 1 2 Since both x and y are real you will find that x^2y^2=1 \mid x^2 y^2=1x^2 \mid \div 1 y^2=x^21=(x1)(x1) \mid \sqrt{} y=\pm \sqrt{(x1)(x1)}= \pm \sqrt{x1}.
Srihithasai152 srihithasai152 Math Secondary School answered • expert verified The circle x^{2}y^{2}=4x2y2=4 cuts the line joining the points A(1,0)A(1,0) and B(3,4)B(3,4) in two points PP and Q let \frac{B P}{P. Let the circle `( x 1 )^2 ( y 2 )^2 = 25` cuts a rectangular hyperbola with transverse axis along `y = x` at four points `A,B,C` and `D` having coordinates `( x_i, y_i ) i = 1,2,3,4` respectively `O` being the centre of the hyperbola Now match the entries from the Following two columns. Question 40 A double ordinate PQ of the hyperbol 2)(y 2 /b 2) = 1 is such that Δ OPQ is equilateral, O being the centre of the hyperbola Then the eccentricity e satisfies the relation a 1 < e < 2/√3;.
B and C are placed symmetrically with respect to the xaxis on the branch of the hyperbola not containing A Suppose that the triangle ABC is equilateralIf the sidelength of the triangle ABC is ka, then k lies in the interval (A) (0, 2. Click here👆to get an answer to your question ️ If the circle x^2 y^2 = 1 cuts the rectangular hyperbola xy = 1 in four points (xi,yi) i = 1,2,3,4 then. Recall from Section 34 that the circle x^2 y^2 = r^2, USING ASYMPTOTES TO GRAPH A HYPERBOLA Graph x^2/25y^2/49=1 Figure 341 For this hyperbola, )x becomes y = (7/5)x Use the xintercepts if x = 5, then y = (7/5)(5) = 7, and if x = 5, y = 17 These four points, (5, 7),(5, 7), (5, 7), and (5, 7), lead to the rectangle.
Let f (x, y) and g (x, y) be For a rectangle whose perimeter is m, use the Lagrange multiplier method to find the dimensions that will maximize the area Solution As we saw in Example 1391, with x and y representing the width and height, respectively, of the rectangle, this problem can be stated as Maximize f (x, y) = x y subject to g (x, y) = 2 x. In this section we will look at converting integrals (including dA) in Cartesian coordinates into Polar coordinates The regions of integration in these cases will be all or portions of disks or rings and so we will also need to convert the original Cartesian limits for these regions into Polar coordinates. Let the equation of the circle is `x^(2) y^(2) = 25` and the equation of the line `x y = 8` If the radius of the circle of maxium area and also touches.
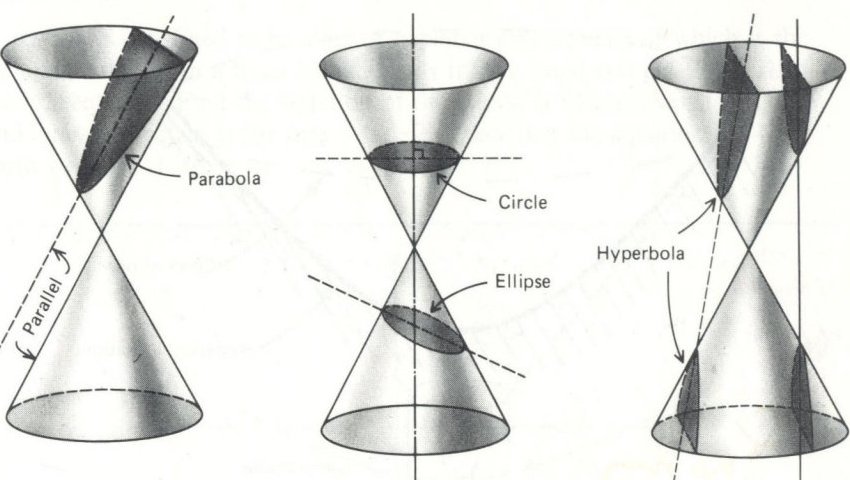
Given Circles is x 2 y 2 2x 2y 2 = 0 Which can be written as (x 1) 2 (y 1) 2 = 4, so C(1, 1) and radius is 2 Let O be the centre and AB be the chord, angle = 90° Draw OA and OB & ∠AOB = 90° Now OA and OB are radius of the circle OA = OB & ∠OAB = & ∠OBA Angle opposite to equal sides are equal But ∠OAB ∠OBA ∠AOB = 180° 2∠OAB = 180 – 90 ∠OAB = 45. A conic section is the locus of a point that advances in such a way that its measure from a fixed point always exhibits a constant ratio to its perpendicular distance from a fixed position, all existing in the same plane learn about the important terminology, concepts, and formulas regarding the conic section, followed by Parabola, Ellipse, and Hyperbola. Z 2 Z 1 Z π/2 Z π a) (6x 2 2y)dydx b) (usint tcosu)dtdu 0 −1 0 0 Z 1 Z x 2 Z 1 Z u p c) 2x 2ydydx d) u2 4dvdu √ 0 x 0 0 3 Express each double integral over the given region R as an iterated integral, using the given order of integration Use the method described in Notes I to supply the limits of integration For some of them, it.
Let S 1 and S 2 be the foci of a rectangular hyperbola, on the hyperbola $\frac{x^2}{a^2}\frac{y^2}{b^2} = 1 $ cuts the circle x 2 y 2 = a 2 at the points Q(x 1, y 1) and R(x 2, y 2), then = 1/y 1 1/y 2 (A) 2/k (B) 1/k (C) a/k (D) b/k Click to See Answer Ans (A) 46 The reflection of the curve xy = 1 in the line y = 2x is the curve 12x 2 r xy sy 2 t = 0, then the value of r. Solution Answer (d) Let P = ( sec θ 1/ √3. On a rectangular hyperbola x 2 – y 2 = a 2, a > 0, three points A, B, C are taken as follows A = (–a, 0);.
The circle x 2 y 28x=0 and hyperbola x 2 /9y 2 /4=1 intersect at the points A and B The equation of a common tangent with positive slope to the circle as well as to the hyperbola Share It On Facebook Twitter Email 1 Answer 1 vote answered by yushGupta (776k points) selected by gaurav sahu Best answer Solution (1) Equation of. コレクション let the circle (x1)^2 (y2)^2=25 Let the circle (x1)^2(y2)^2=25 {eq}\displaystyle (x 15)^2 y^2 = 225 {/eq} Circle Equation Graphically it is very easy to recognize a circular curve since most people are familiar with that figureFree Circle calculator Calculate circle area, center, radius and circumference stepbystep This website uses cookies to ensure you get. STATEMENT1 Tangent at any point on the hyperbola meets the coordinate axes at points Q and R, the circumcentre of has coordinate and STATEMENT2 Equation of tangent at point to the curve is.
Let the equation of circle is x 2 y 2 2gx 2fy c = 0 It cut the circle x 2 y 2 = 4 orthogonally if 2g0 2f0 = c 4 ⇒ c = 4 ∴ Equation of circle is x 2 y 2 2gx 2fy 4 = 0 Q It passes through the point (a, b) ∴ a 2 b 2 2ag 2f 4 = 0 Locus of centre (g, f) will be a 2 b 2 2xa 2yb 4 = 0 2ax 2by (a 2 b 2 4) = 0 450 Views Answer 6 A variable. Yintercepts Simply let x = 0 in the equation given in the. A rectangular hyperbol 2 – y 2 /b 2 ⇒ x 2 / 2 = 1 Or, x 2 – y 2 = a 2 Eccentricity of rectangular hyperbola Also, xy = c.
1 Let F~(x;y;z) = h y;x;xyziand G~= curlF~ Let Sbe the part of the sphere x 2 y2 z2 = 25 that lies below the plane z= 4, oriented so that the unit normal vector at (0;0;. 1 Integrate f(x;y) = sin(p x2 y2) over (a) the closed unit disc;. Given by x2 2y2 3z2 = 1 Solution Let’s deflne g(x;y;z) = x2 2y2 3z2, so the problem is to flnd the maximum of F(x;y;z) subject to the constraint g(x;y;z) = 1 We have rF = ‚rg , (2(xy z);2(xy z);2(xy z)) = ‚(2x;4y;6z) Reading this component by component and including the restriction we get the system of equations xy z = ‚x (A) xy z = 2‚y (B) xy z = 3‚z (C) x 2.
D e > 2/√3;. Sketch the hyperbola `y^2/25x^2/4=1` Answer First, we recognise that it is a northsouth opening hyperbola, with a = 5 and b = 2 It will look similar to Example 1 above, which was also a northsouth opening hyperbola We need to find The yintercepts (there are no xintercepts for this example) The asymptotes;. (b) the annular region 1 6 x2 y2 6 4 Solution (a) ZZ sin(p x2 y2)dA = Z2ˇ 0 Z1 0 (sinr)rdrd = 2ˇ(sin(1) cos(1)) (b) ZZ sin(p x2 y2)dA = Z2ˇ 0 Z2 1 (sinr)rdrd = 2ˇ(cos(1) 2cos(2)sin(2) sin(1)) 2 Calculate the following integrals by changing to polar coordinates (a) Z2 0 Zp 4 x2 0 p x2 y2 dydx;.
X 2y2 = 5 = 25 And this equation is true for any point on the circle For instance, we could take a point Q(x1,y1) in a different quadrant 5 Q(x 1, y 1) x 1 y 1 5 5 −5 −5 N O Once again, we can drop a perpendicular from Q to the xaxis And now we can use the rightangled triangle OQN to see that x2 1 y 2 1 = 5 2 So the coordinates. If a rectangular hyperbola `(x1)(y2)=4` cuts a circle `x^(2)y^(2)2gx2fyc=0` at points `(3, 4), (5, 3), (2, 6)` and `(1, 0)`, then the value of `(gf)`. Answer (1 of 3) Any circle that touches hyperbola x^2 y^2 = 25 in two places and the circle x^2 y^2 = 25 in one place will have its centre on the yaxis NOTE there is another circle with the same radius that is tangent to the hyperbola and the given circle with its centre along the negati.
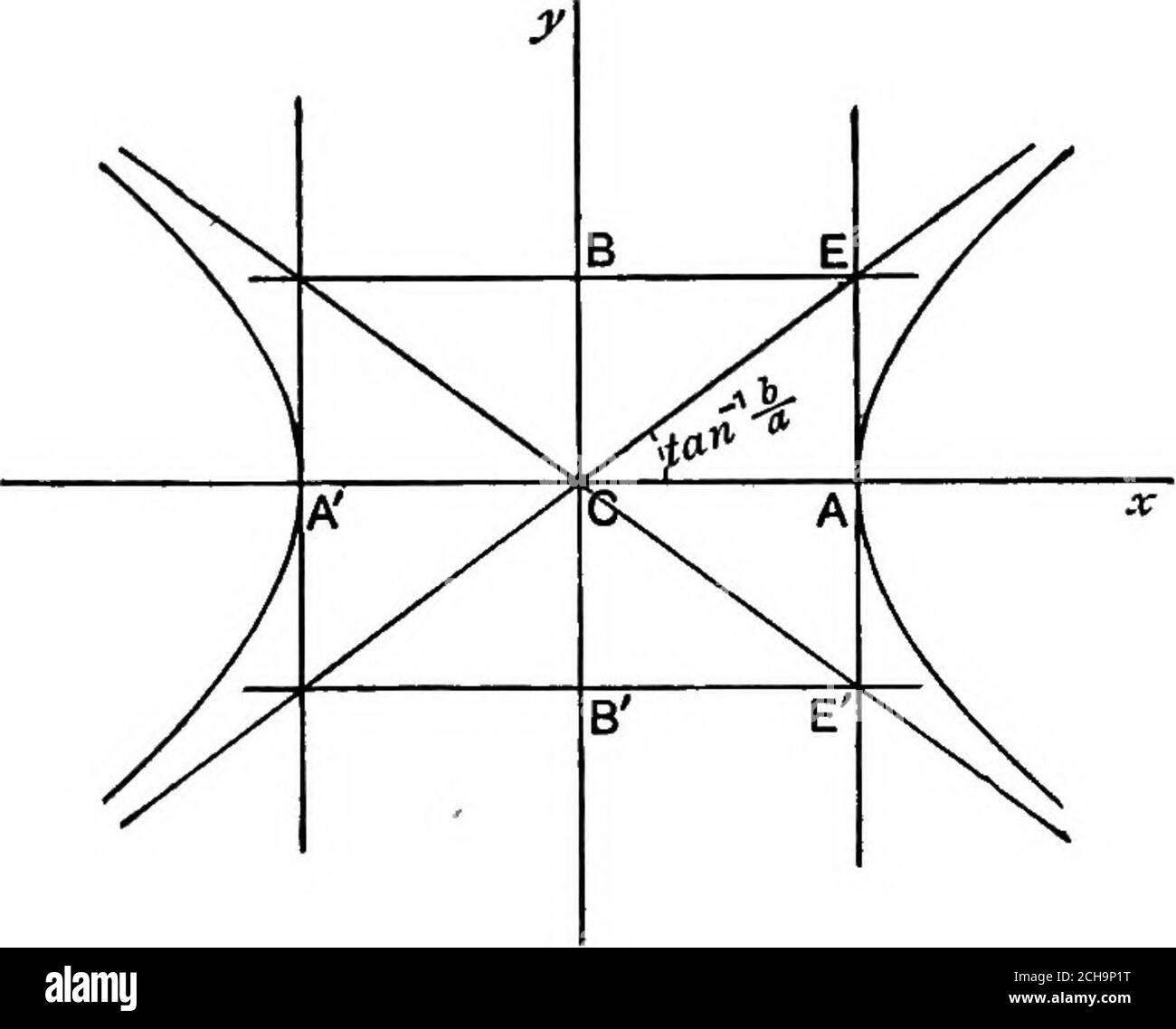
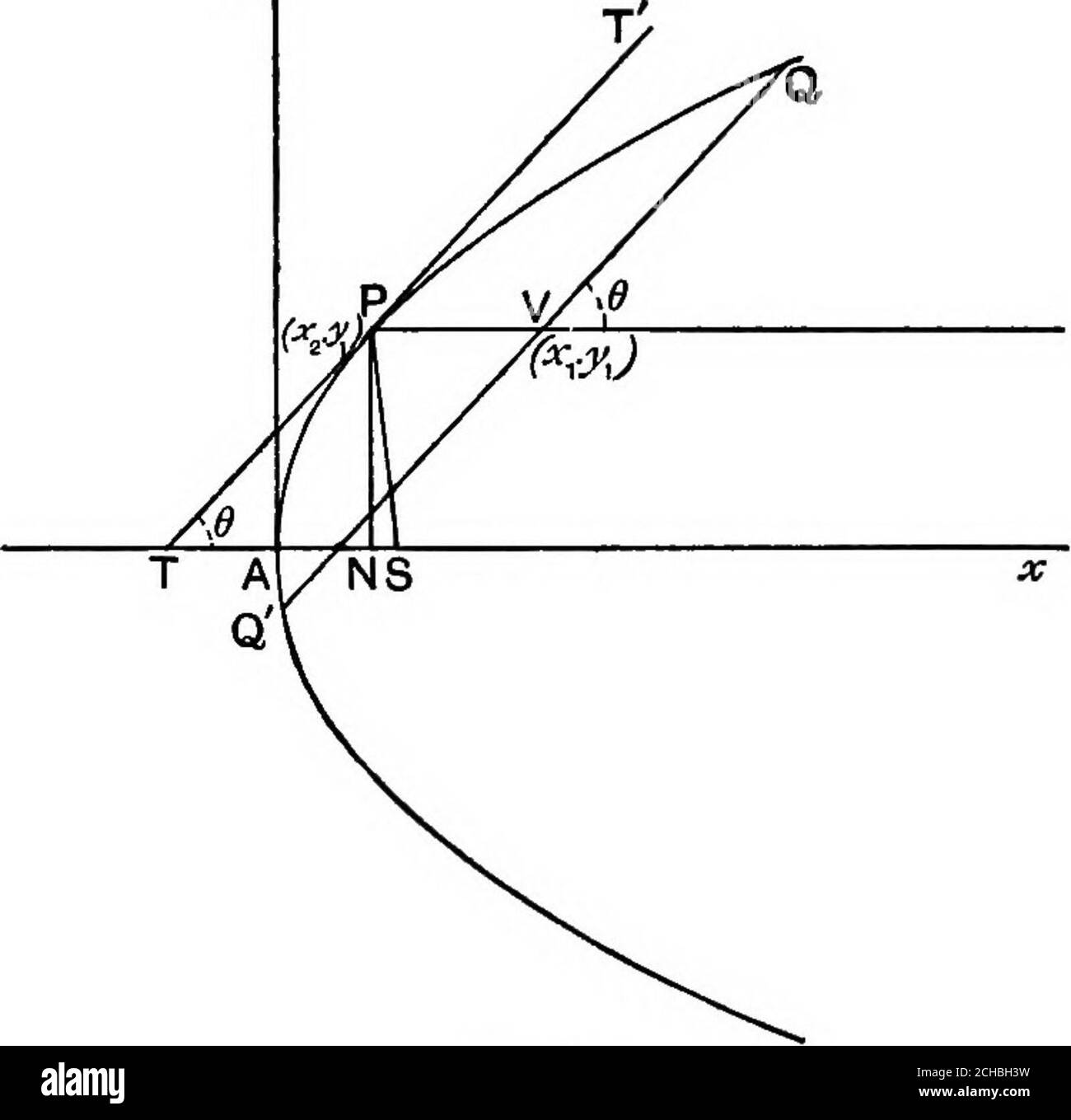
The hyperbol 2 – y 2 /b 2 = 1, is 2 tan –1 (b/a) This is = π/4, ie, if b/a = 1 ⇒ b = a The equation of rectangular hyperbola referred to its transverse and conjugate. 1i Use Stokes’ Theorem to nd ZZ S G~d~S Solution Here’s a picture of the surface S x y z To use Stokes’ Theorem, we need to rst nd the boundary Cof Sand gure out how it should be oriented The. Example 18 Find the line integral Z C ((x −y)~ix~j)·d~r where C is the segment of the circle x2 y2 = 9 with 0 6 ϑ 6 π/2 oriented counterclockwise Notice that if we parametrize this portion of the circle and evaluate this integral, we get a very messy trig integral Therefore, we shall try to use Green’s Theorem indirectly.
X2 y2 = 2, so 172;252;312 is an arithmetic progression (common di erence 336) Finding all 3term arithmetic progressions of perfect squares is thus essentially1 equivalent to nding all rational points on the circle x2y2 = 2 An obvious rational point on this circle is (1;1) Using lines through this point we will describe all other rational points on the circle Theorem 21 The points on. 選択した画像 let the circle (x1)^2 (y2)^2=25 5547Let the circle (x1)^2(y2)^2=25 Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra,.

Double Integrals In Polar Coordinates Article Khan Academy

Vertices Direction Of A Hyperbola Example 2 Video Khan Academy
1
Let The Circle X 12+y 2225 Cuts Rectangular Hyperbola のギャラリー

Mensuration Cone Circle Ellipse Parabola And Hyperbola Previous Papers Question Paper

The Academy Corner Dong Thap In South Vietnam Portal Manualzz
The Tangent At The Point P On The Rectangular Hyperbola Xy K 2 With Centre Sarthaks Econnect Largest Online Education Community
Cissoid High Resolution Stock Photography And Images Alamy

13

Hyperbola Wikipedia
The Hyperbola Algebra And Trigonometry

Hyperbola Equation Properties Examples Hyperbola Formula

Fp3 Chapter 2 Further Coordinate Systems Ppt Download

If A Rectangular Hyperbola And A Circle Meet In Four Points The Coordinates Of The Center Of The Hyperbola Is 1 9 And That Of The Circle Is 3 7 Find The Mean

Hyperbola Wikipedia

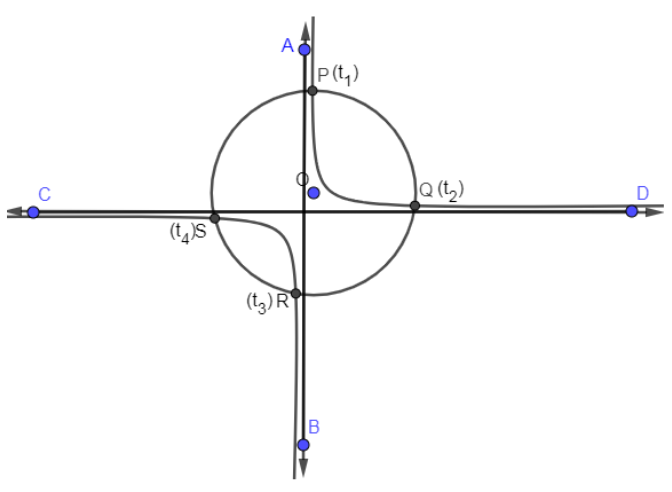
Let The Circle X 1 2 Y 2 2 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four

Section Of Solid
Hyperbola Standard Equation Conjugate Hyperbola With Examples
.jpg)
Ask The Physicist

14 19 Sphere Engineering Mathematics Volume I Second Edition Dev Guis
X Axis Cut Out Stock Images Pictures Page 3 Alamy
X Axis Cut Out Stock Images Pictures Page 3 Alamy

Mathematics Ar Engineering College

Hyperbola Wikipedia

Precalculus University Of Washington
Cissoid High Resolution Stock Photography And Images Alamy
What Is The Radius Of The Circle S That Touches The Hyperbola X 2 Y 2 25 In Exactly Two Places And Touches The Circle X 2 Y 2 25 In One Quora
1

Geometriae Pars Universalis
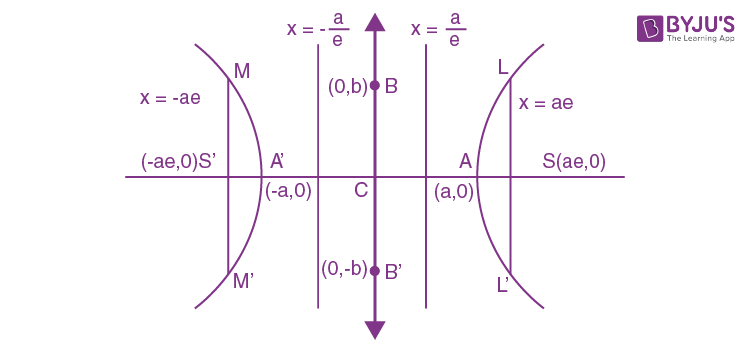
Hyperbola Standard Equation Conjugate Hyperbola With Examples

Coordinate Geometry Flip Ebook Pages 301 350 Anyflip Anyflip

Solved Integrate F X Y X Over The Region In The First Chegg Com

Free Objective Test 02 Practice Test 11th And 12th Self Study 365

Sketching Quadratic Functions Ppt Download

If The Circle X 2 Y 2 1 Cuts The Rectangular Hyperbola Xy 1 In Four Points Xi Yi I 1 2 3 4 Then

Hyperbola Wikipedia

Mathematics Ar Engineering College
Pplato Flap Math 2 3 Conic Sections
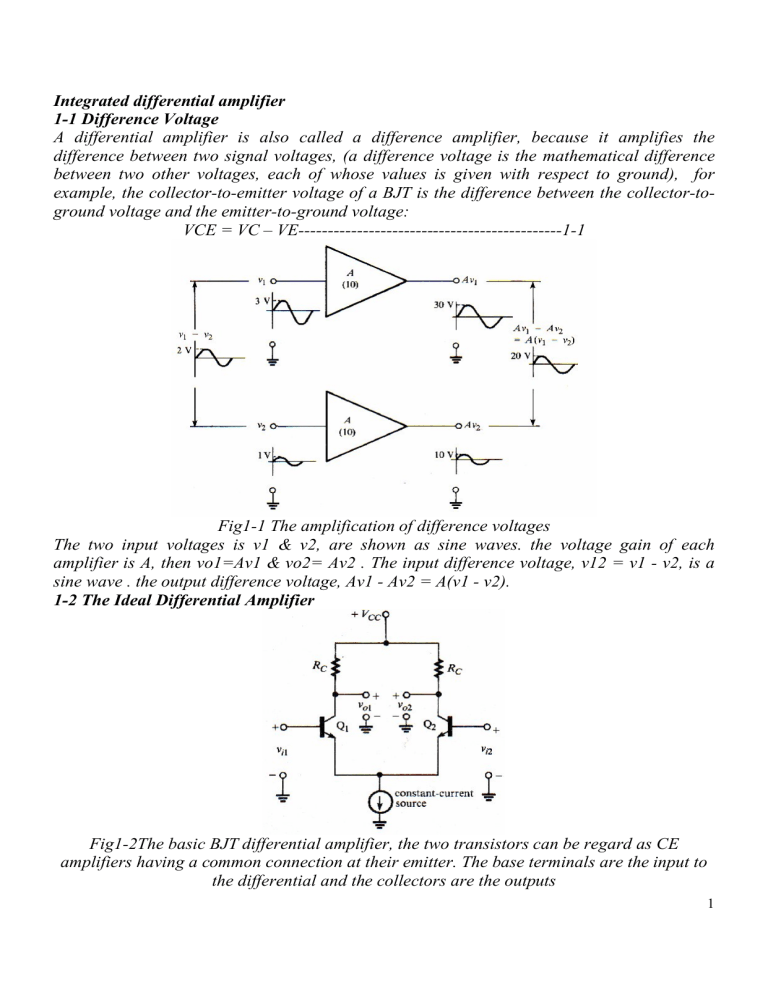
Integrated Differential Amplifier 1 1 Difference Voltage A Differential
Vertex Of The Hyperbola Definition Of The Vertex Of A Hyperbola

Olympiad Total Gadha
Hyperbola Calculator Calculate With Hyperbola Equation

14 19 Sphere Engineering Mathematics Volume I Second Edition Dev Guis
If The Circle X 2 Y 2 A 2 Cuts The Hyperbola Xy C 2 At Four Points Xk Yk Where K 1 2 3 And 4 Then Sarthaks Econnect Largest Online Education Community

Then They Intersecil Is C O X Aly B C Ax Byc 11 1 At Two Points The B 16x 10xy 2y 2 0

Calc3 1001 By James Bardo Issuu
What Is The Equation Of The System Of The Orthogonal Trajectories Of The Family Of Circles Math X 1 2 Y 3 2 R 2 Math Quora
Ellipse Equation

Bia Math đa Gộp
What Is The Differential Equation Of Circles Tangent To The X Axis Quora

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1

Solved If A Circle And Rectangular Hyperbola Xy C2 Meets In Self Study 365

Conic Sections
2

Solved If A Circle And Rectangular Hyperbola Xy C2 Meet In T Self Study 365
Hyperbola Equation Properties Examples Hyperbola Formula
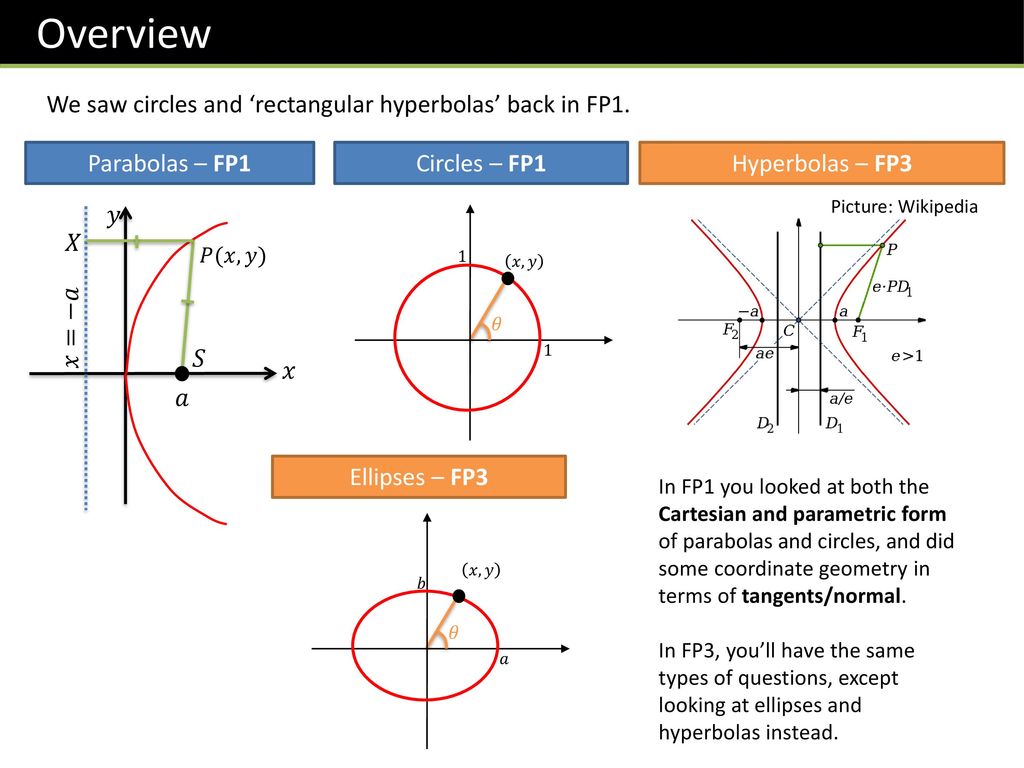
Fp3 Chapter 2 Further Coordinate Systems Ppt Download
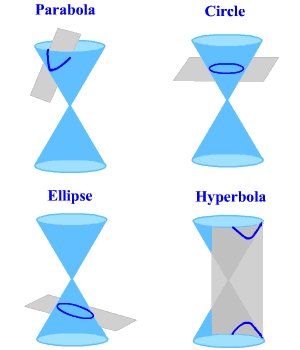
Conic Sections And Standard Forms Of Equations
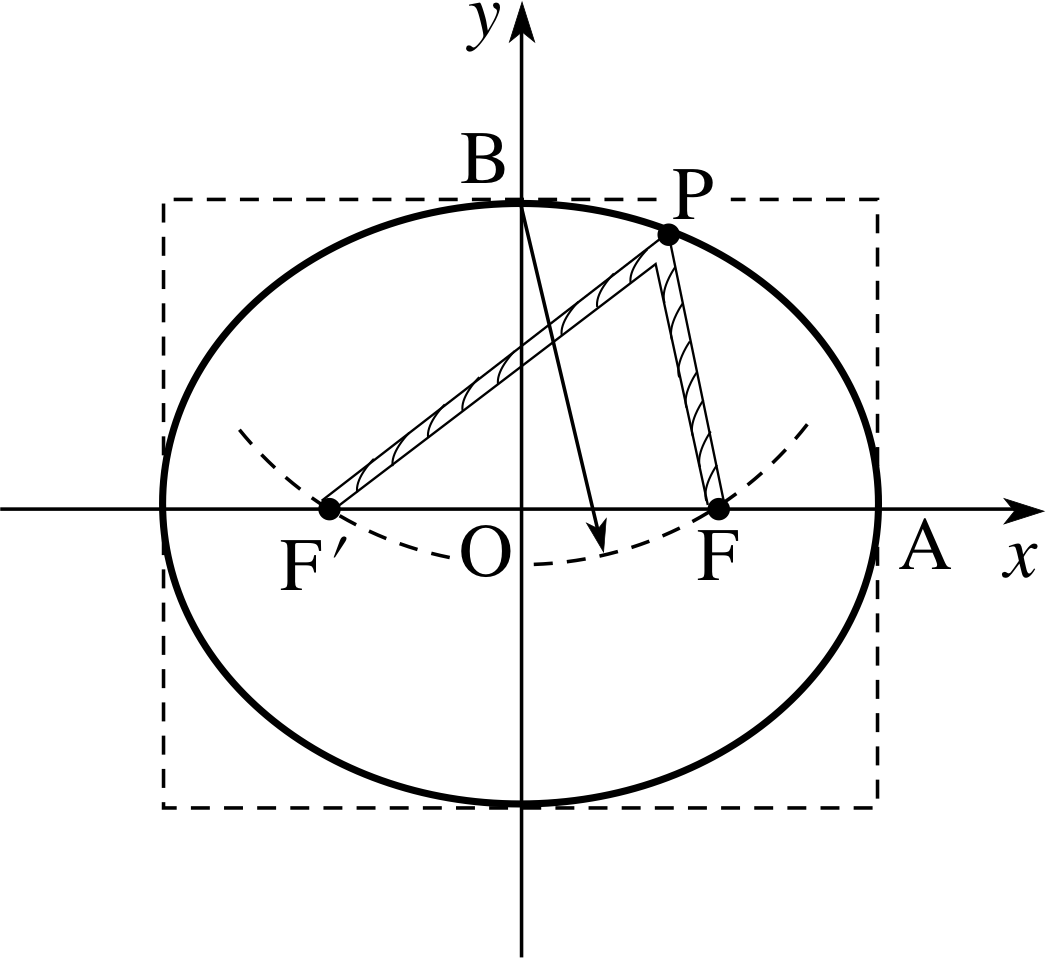
Pplato Flap Math 2 3 Conic Sections
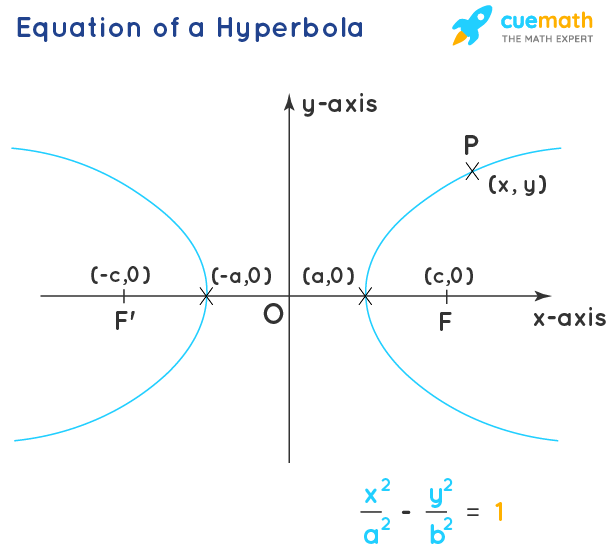
Hyperbola Equation Properties Examples Hyperbola Formula
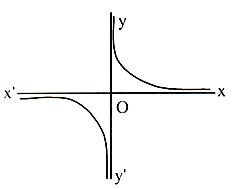
Intersection Of Cricle And Rectangular Hyperbola Study Material For Iit Jee Askiitians

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1
If A Circle Cuts A Rectangular Hyperbola Xy 16 In Four Class 11 Maths Cbse

Mensuration Cone Circle Ellipse Parabola And Hyperbola Previous Papers Question Paper

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1
The Parabola Algebra And Trigonometry Openstax

Calameo Algebra 2 Mcgraw Hill

Coordinate Geometry Flip Ebook Pages 301 350 Anyflip Anyflip
See Tutors Answers
Intersection Of Cricle And Rectangular Hyperbola Study Material For Iit Jee Askiitians

Mensuration Cone Circle Ellipse Parabola And Hyperbola Previous Papers Question Paper

Math Beatles Math
2

Trestle
Numbers Quadratic Relations Conic Sections
2
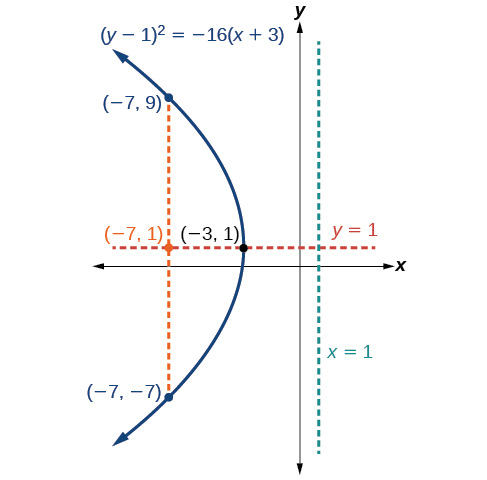
The Parabola Algebra And Trigonometry Openstax

The Parabola Algebra And Trigonometry Openstax
2
Megalecture Com
Cissoid High Resolution Stock Photography And Images Alamy
If A Circle And The Rectangular Hyperbola Xyc2 Meet Class 11 Maths Cbse

Fp3 Chapter 2 Further Coordinate Systems Ppt Download

Hyperbola Wikipedia
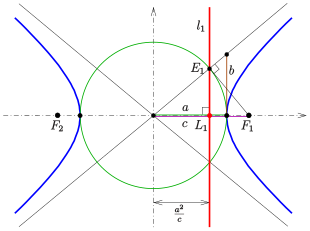
Hyperbola Wikipedia
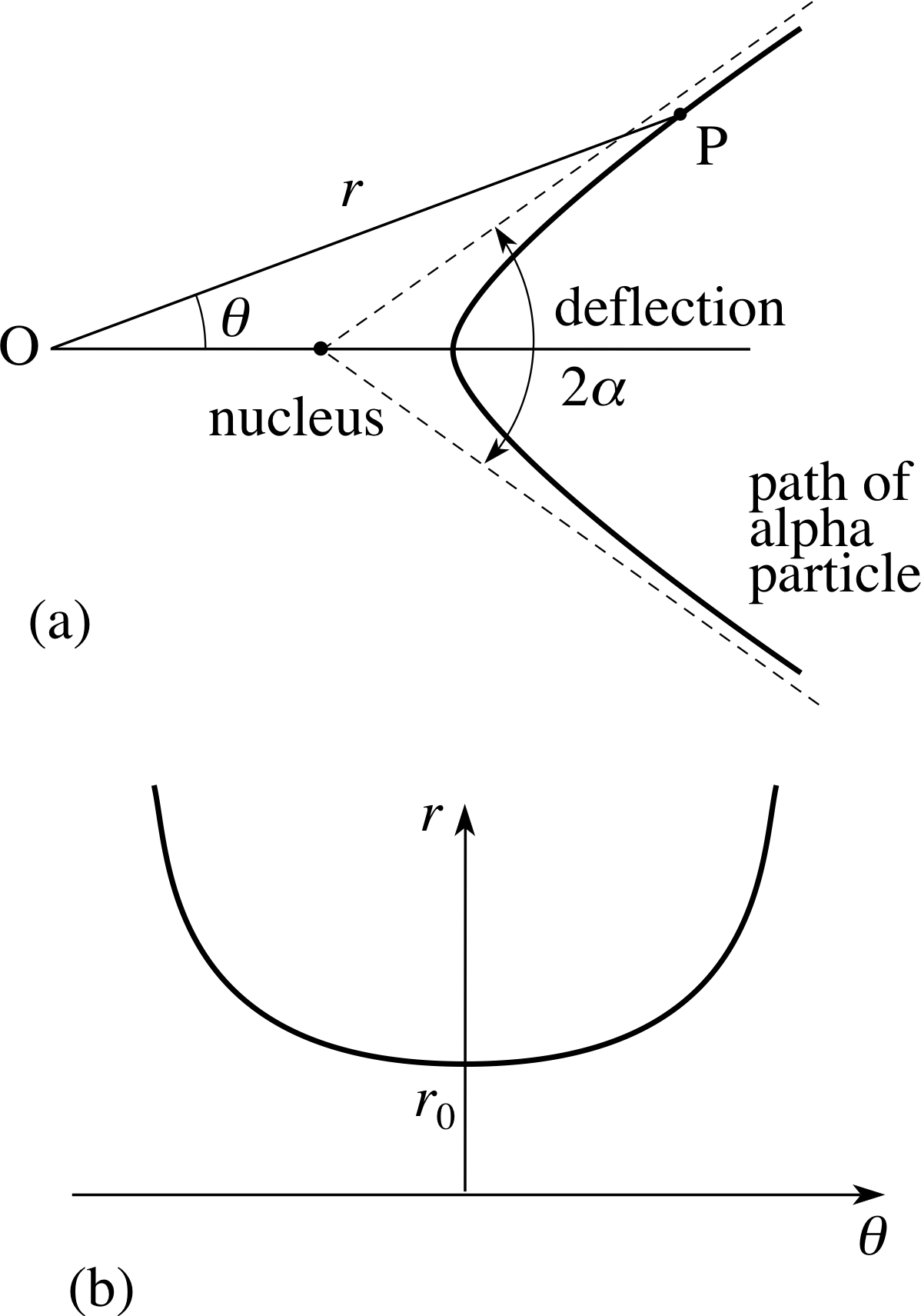
Pplato Flap Math 2 3 Conic Sections

Mathematics Part1 Pages 1 250 Flip Pdf Download Fliphtml5

Quadratic Function

Hyperbola Equation Properties Examples Hyperbola Formula
2
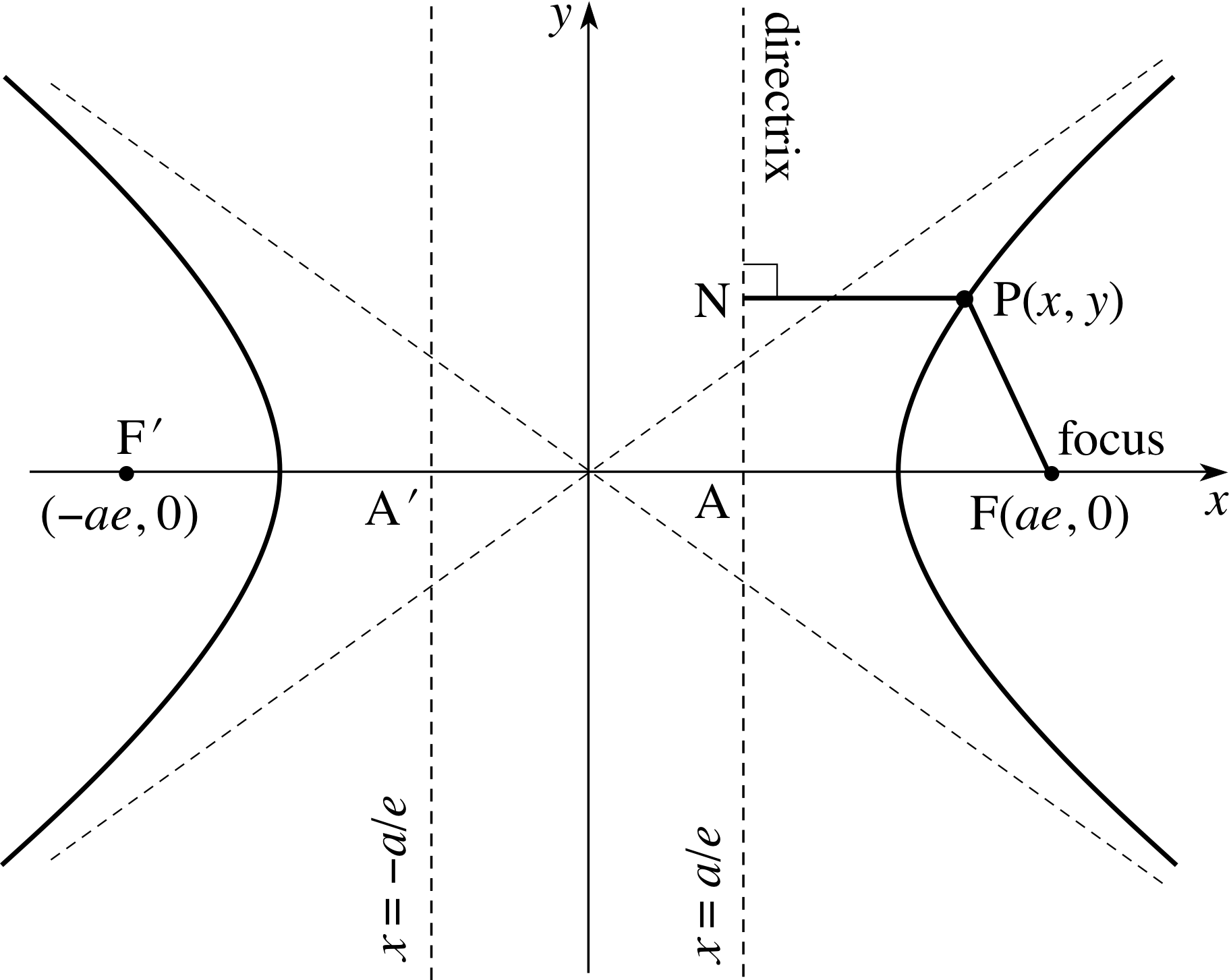
Pplato Flap Math 2 3 Conic Sections

14 19 Sphere Engineering Mathematics Volume I Second Edition Dev Guis
Osa Hypersingularity Electromagnetic Edge Condition And An Analytic Hyperbolic Wedge Model
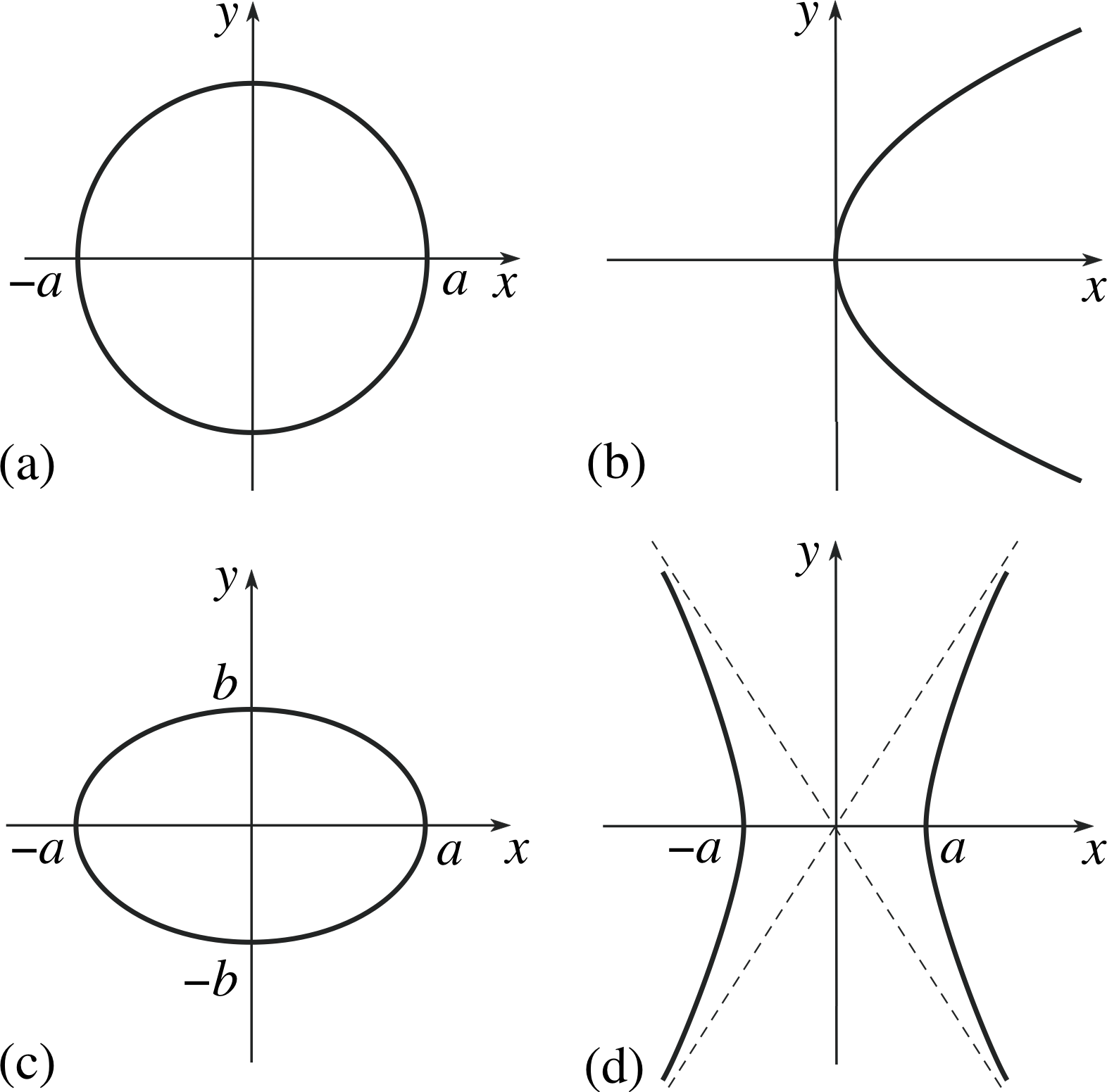
Pplato Flap Math 2 3 Conic Sections
What Is The Condition So That The Line Px Qy R Is Tangent To The Circle X Y A Quora

Advanced Problems Mathematics
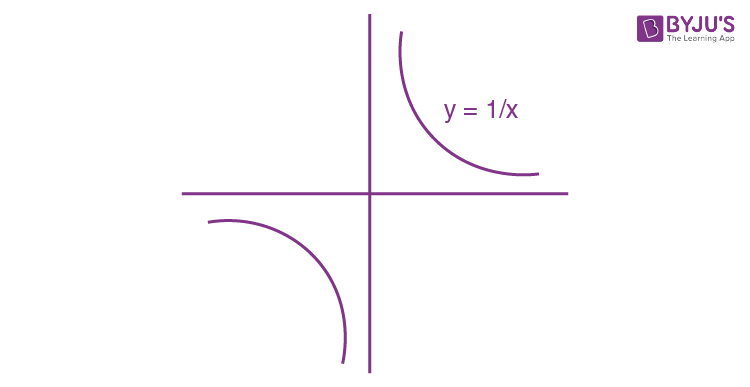
Hyperbola Standard Equation Conjugate Hyperbola With Examples
Ellipse Formula
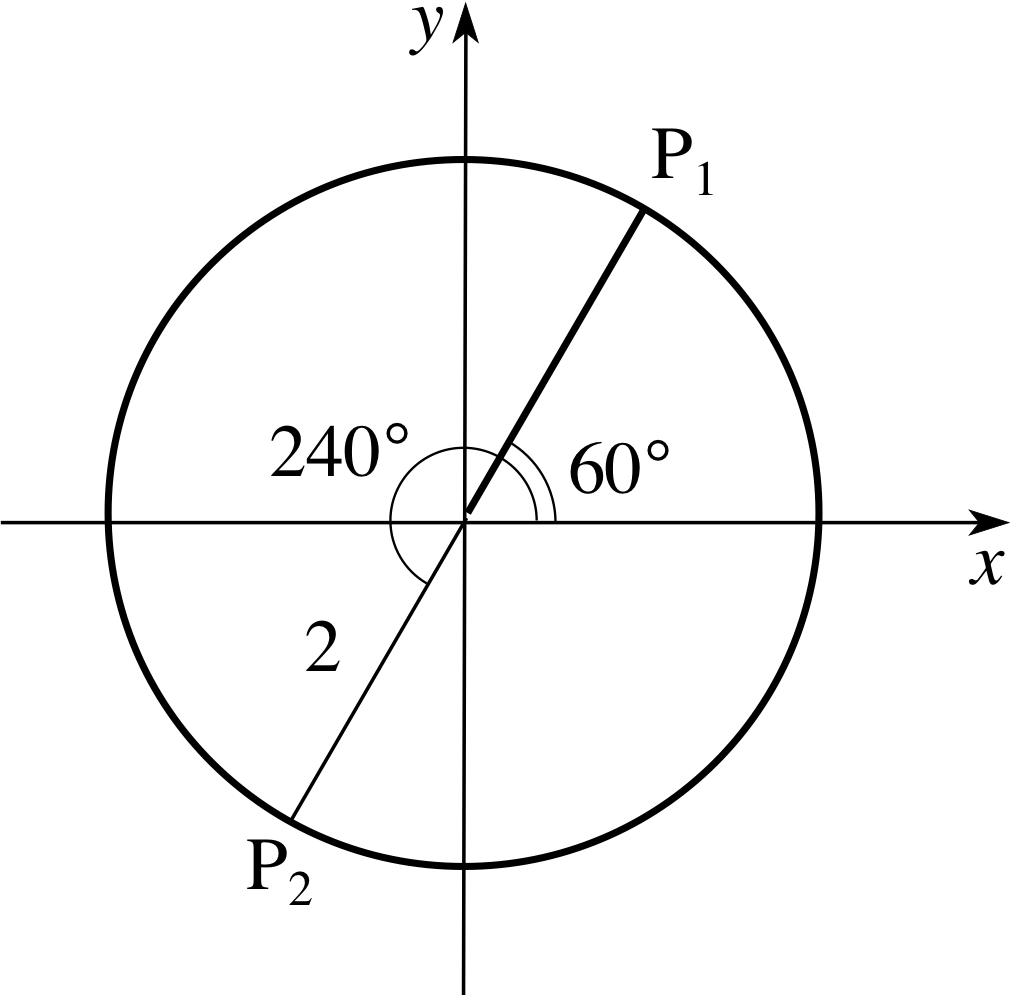
Pplato Flap Math 2 3 Conic Sections

Geometriae Pars Universalis

Let The Circle X 1 Y 1 25 Cuts A Rectangular Hyperbola With Transverse Axis Along Y X At Four Points A B C And D Having Co Ordinates X1 Y1
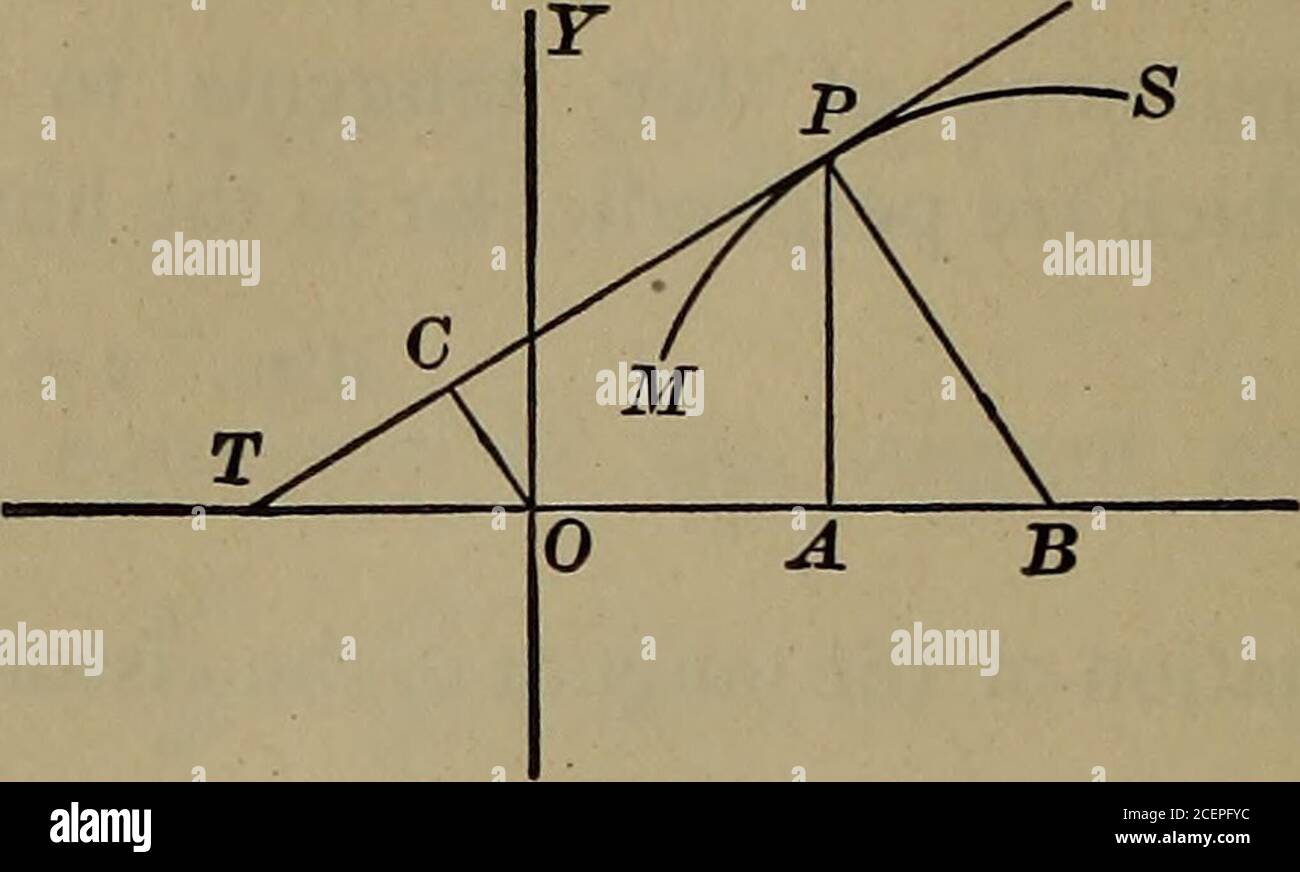
Booksubjectcalculu High Resolution Stock Photography And Images Alamy

Mensuration Cone Circle Ellipse Parabola And Hyperbola Previous Papers Question Paper




