線対称 点対称
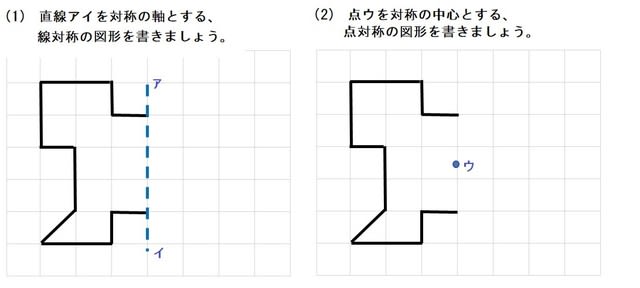
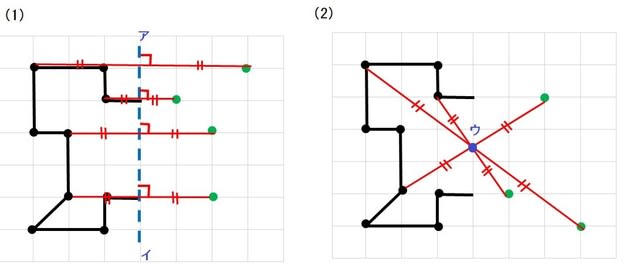
1 次の図形から,点対称な図形と線対称な図形を答えましょう。 線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点は,どれですか。 ⑶ 直線BCに対応する直線は,どれですか。.
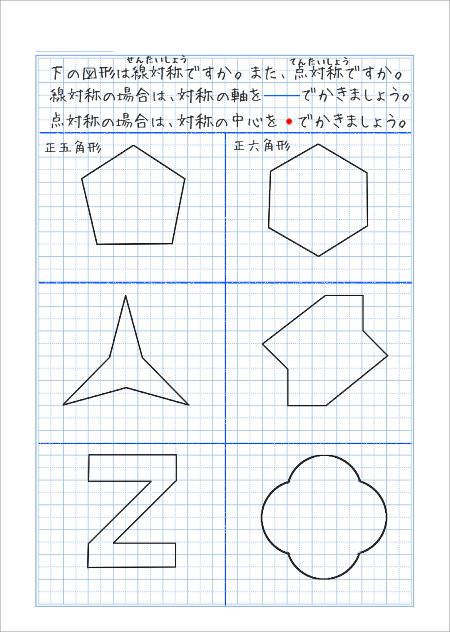
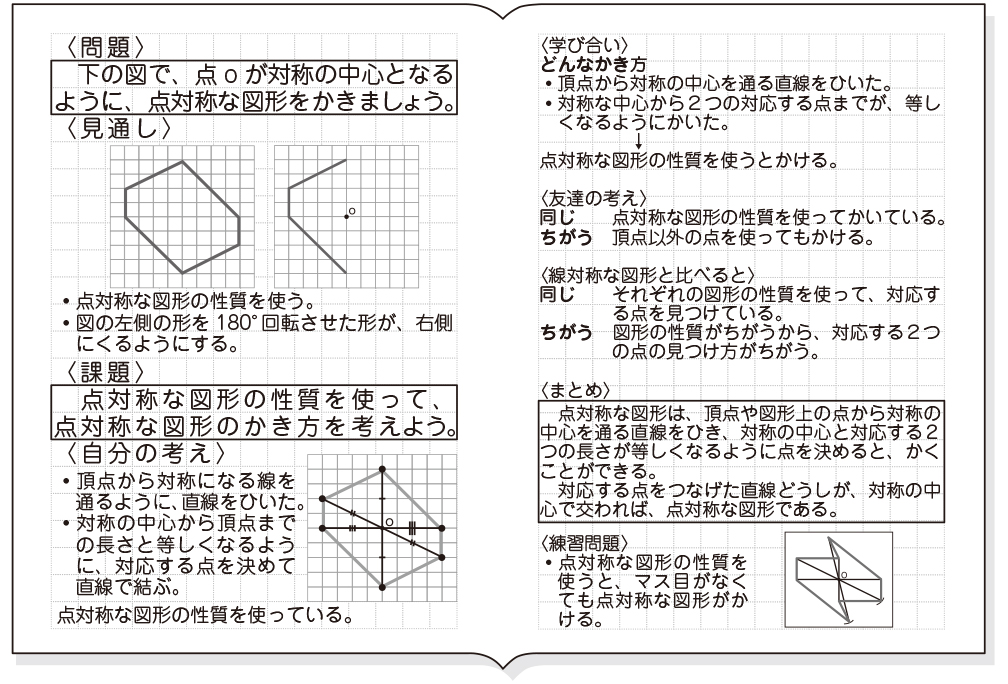
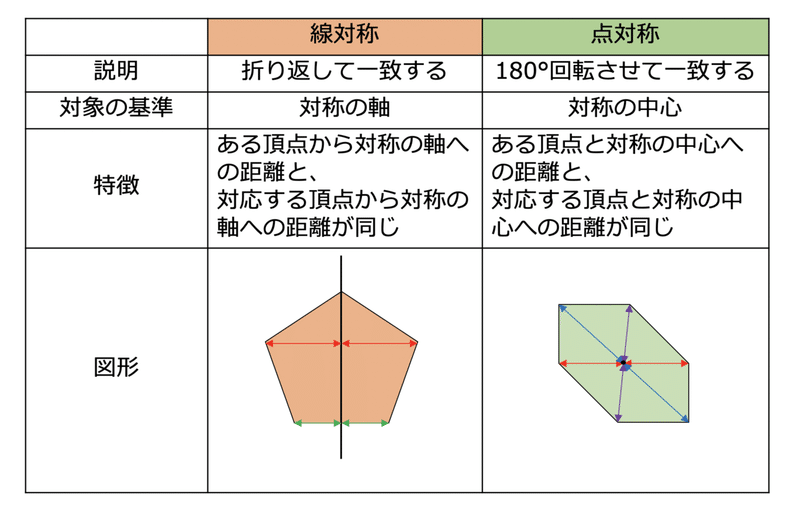
線対称 点対称. 線対称・点対称 線対称の定義 対称の軸で折り重ねたときに重なる点を対応する点,重なる線を対応する線,重なる角を対応する角といいます。 なお,小学校では,1つの図形の性質を表すものとして線対称を扱い,2つの図形の関係としての線対称の位置にある図形は扱いません。 線対称な図形の性質は,次のようにまとめています。 点対称の定義 対称の中心のまわりに180°まわして重なる点,線,. 時計のトリックを見破れ ~対称~ 容疑者が撮影した写真には、:を示すデジタル時計がうつっていた。 その時計のトリックを、ゼロが「線対称」「点対称」の関係を使って明らかにしてゆく。. 2 〇線対称な図形をかこう。 教科書p13 ステップ3(1) 3 〇点対称について学ぼう。 教科書p14~17 ステップ2 4 〇点対称な図形をかこう。 教科書p18 ステップ3(2) 5 〇多角形と線対称・点対称について学ぼう。 教科書p19~ ステップ4.
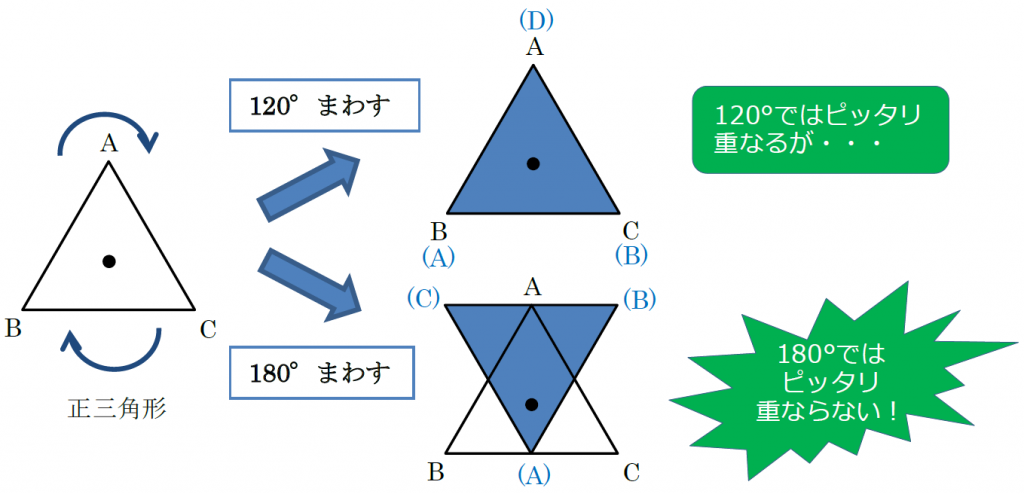
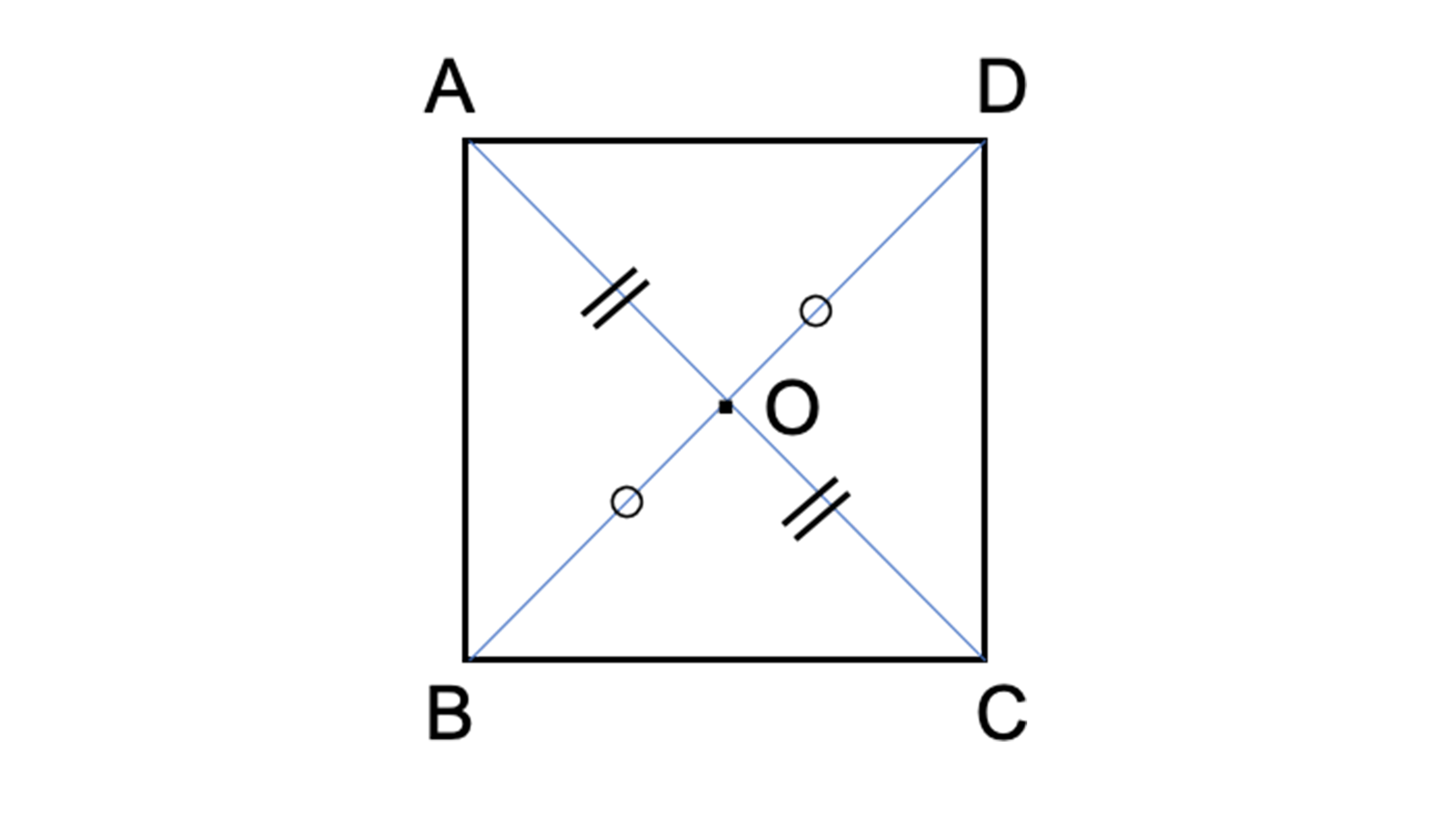
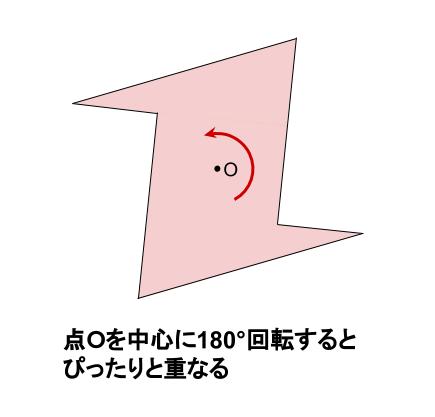
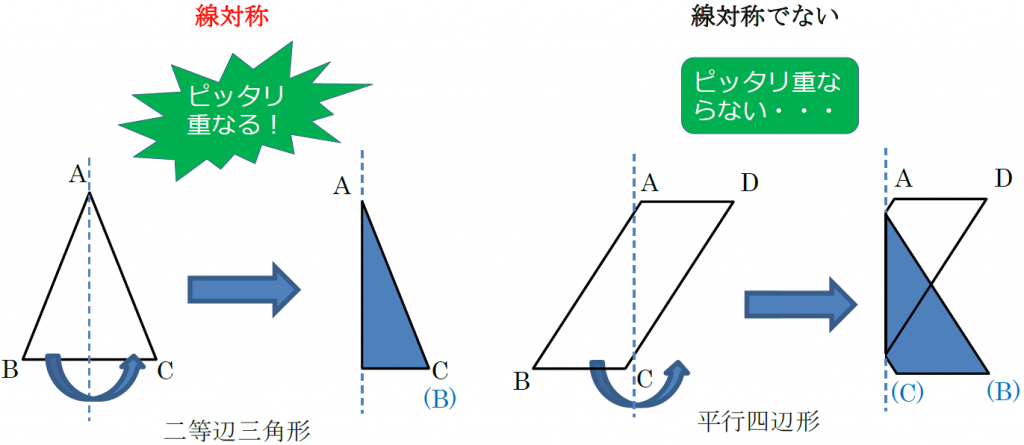
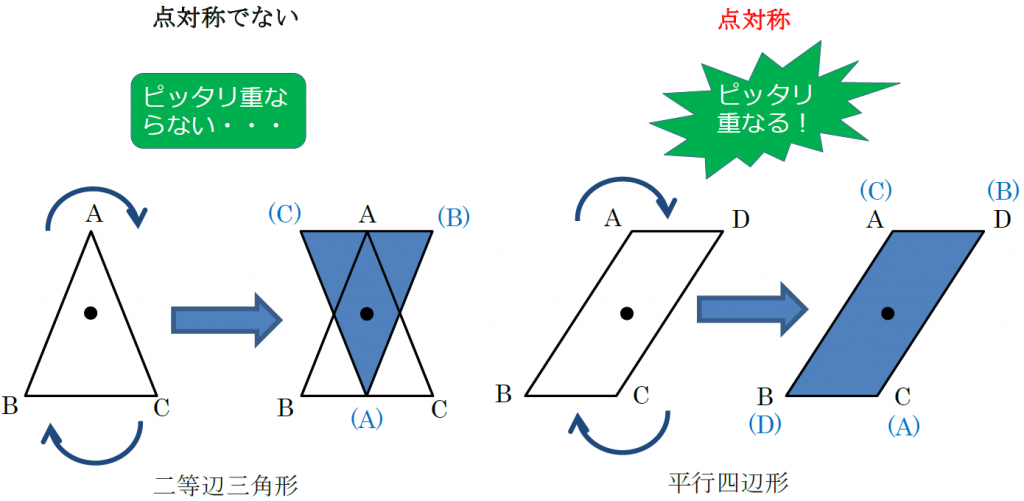
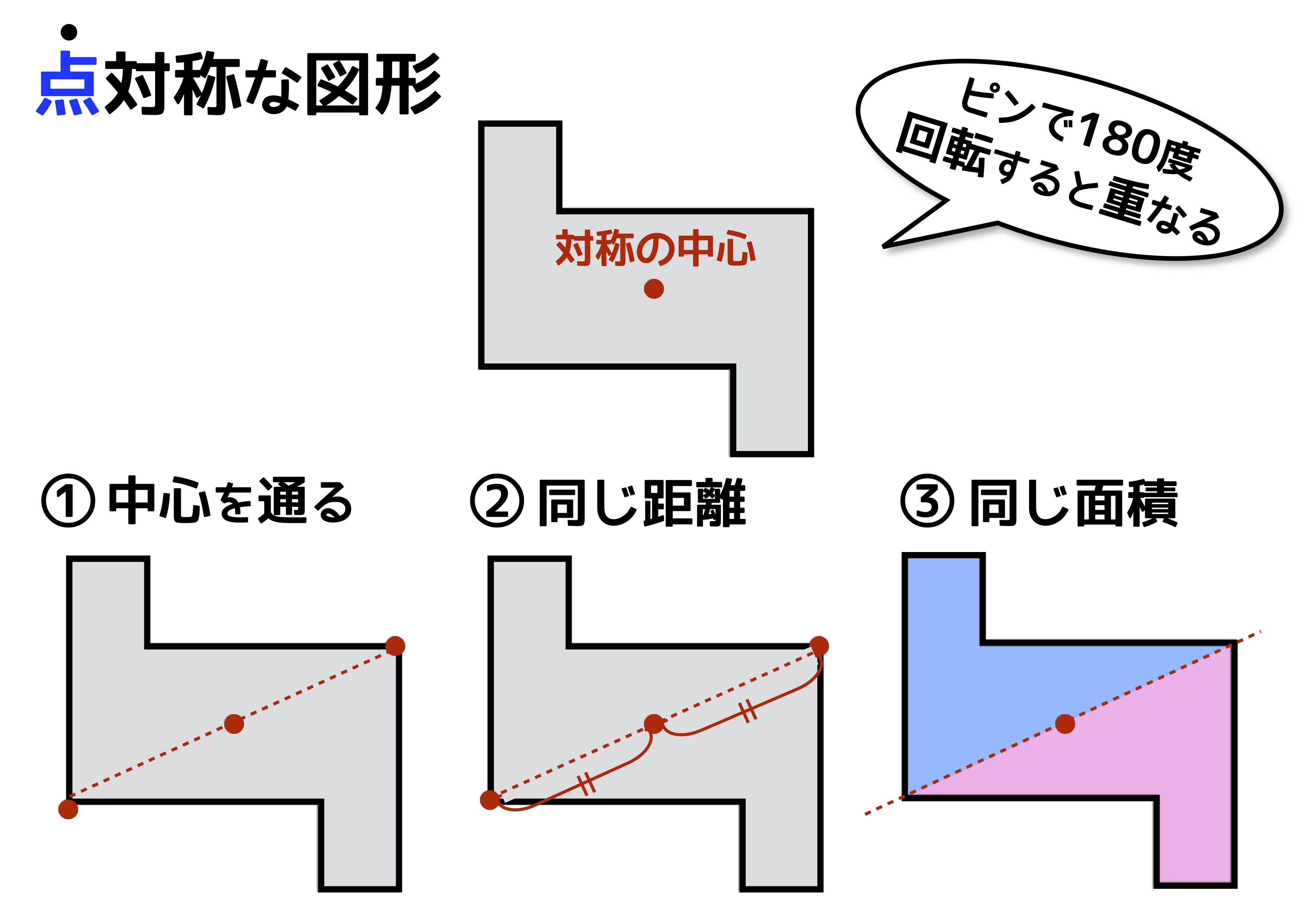
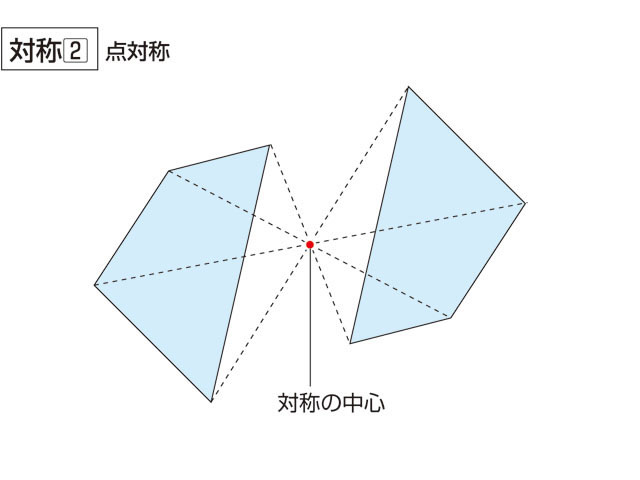
線対称は、ある図形に線を引いて、その線を境に折り曲げたとき、ぴったり重なることです。 私たちの生活の中で、紙をぴったり重ね合わせることも多いので、イメージしやすいでしょう。 対称には、線対称だけでなく点対称や面対称もあります。 当サイトでは、建築学で使う数学について解説しています。 下記も併せてご覧ください。 建築で数学は必要? 現役設計者が教える必要な公式、範囲、. 解説 次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を点対称な図形といいます。 このとき回転の中心となる点を対称の中心といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。. C1:は~い!線対称です! C2:点対称にもなっています! 大多数の子どもはここまでの学習を振り返り、正方形が点対称でも線対称でもあること を確認した。また、対象の軸は何本かを問うと 線対称か否か 対称の軸の数 点対称か否か 正方形 4.
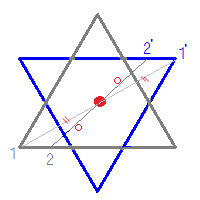
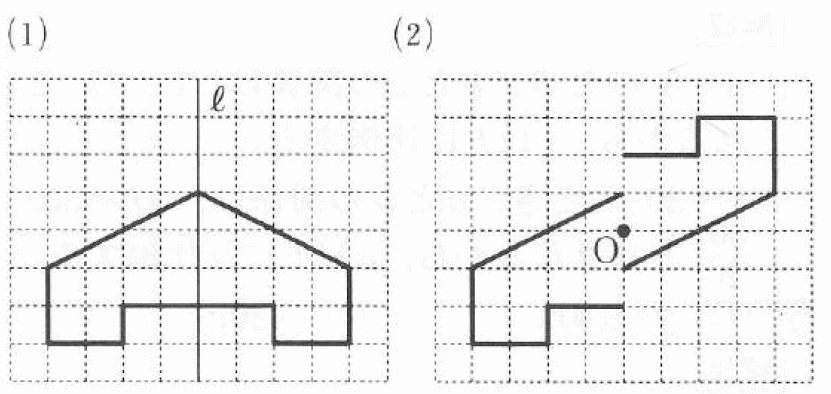
② 点Oが対称の中心となるような点対称な図形 4 次の㋐~㋔の図形について,あとの問いに答えましょ う。 ㋐ 平行四辺形 ㋑ 正三角形 ㋒ 正方形 ㋓ 正五角形 ㋔ 正六角形 ① 線対称でも点対称でもある図形はどれですか。すべて 選びましょう。. 直線アイが対称の軸になるように,線対称な図形をかきましょう。 点Oが対称の中心になるように,点対称な図形をかきましょう。 次の図形について,下の表を完成させましょう。 正三角形 正方形 平行四辺形 ひし形 線対称かどうか ×. 直線に関する対称移動行列の導出 1916 前回の記事では、直線に関して対称な点の公式を導出しました。 しかし、このままではとても覚えづらく、使い勝手も悪いです。 そこで、適用できる条件を狭めることで、応用性の高い公式を導きたいと.
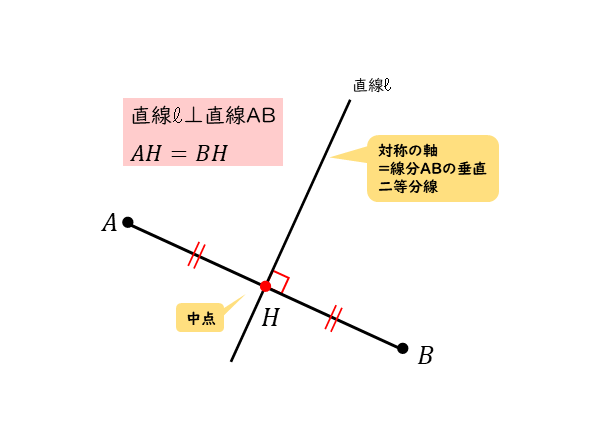
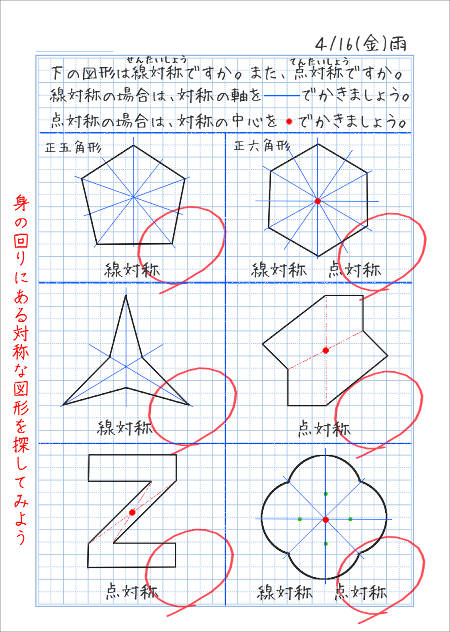
第一学年の「平面図形」の授業では、線対称・点対称の意味とその性質・特徴を理解することを目標とし、ここでは英単語を興味を持って探して、触れることができるようにしたいと考えた。 実際の授業 第一段階 平面図形の観察 アルファベット26個について、線対称のものには対称軸を、点対称のものには対称の中心をかかせた。 (※Kの字体は、斜めの線が1点から出ている字体を使. 数学で「対称」と言えば「線対称」を意味することは中学の数学で学んでいると思いますが、 ここで必要な条件は2つあります。 図を書くと分かりやすいけど、 問題文だけを見ているとなかなか出てきませんよ。 ・直線 と 点 と点 を結ぶ線分が直交する。 ・2点 の中点Mは直線 上にある。 これらは が2点を結ぶ線分の『 垂直二等分線 』だということです。 この2つを満たせばいいわけですが方法. 直線に関して対称な点 直線ℓに関して点Aと対称な点Bを図示すると、以下のようになります。 直線ℓに関して対称な2点A,B 点Aと点Bは、直線ℓに関して対称なので、 対応する点 となります。 線対称な図形では、 対称の軸 がありますが、これは直線ℓのことです。 対称の軸 である直線ℓは、線分ABに対して、 垂直に、かつ二等分する ように交わります。 ですから、直線ℓは、 線分AB.
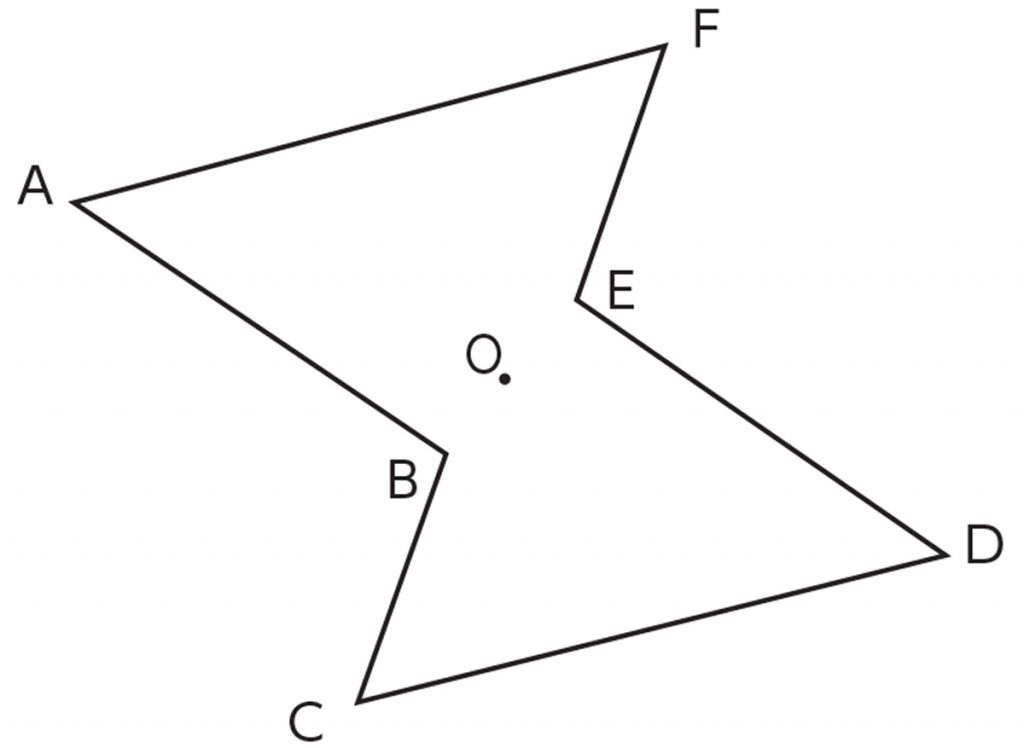
スポンサーリンク 数学点の「対称移動(たいしょういどう)ってどうやるの? 高校数学 数学おじさん 点の対称移動を理解するには、 次の3つの点を理解するといいんじゃ ①、X軸対称 ②、Y軸対称 ③、原点対称. このとき回転の中心となる点を 対称の中心 といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ進むと対応する点があります。 それぞれの点に対応する点があります。 ※ 花火のように広がる図形・放射状図形は,点対称と間違わないように気を. 悩みのタネは、「線対称」と「点対称」に由来している、と思う。 それぞれ、私の教育課程では中学初期に現れた。 「線対称」・・・ ある線を基準に図形を分けたとき、双方の図形が一致する性質。 鏡像対称ともいう。 「点対称」・・・ ある点を.
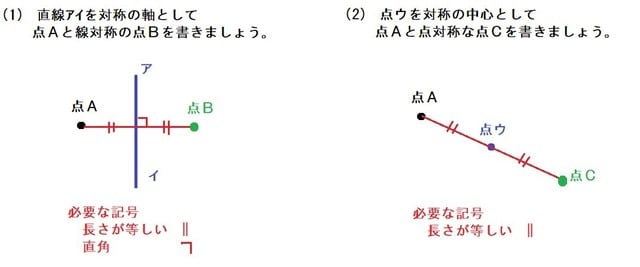
線対称は、対称の軸に対称に点を打って、線をつなげていきます。 点対称は、対称の点に対称な点を打って、線をつなげていきます。 解きポイント ・線対称は、線に対して対称 ・点対称は、点に対して対称 正しく対称の点が打てれば、線対称も点対称も作図で迷うことはないでしょう。 マス目がある場合は、正しくマス目を追っていけば、作図ができます。 ただし、点対称の作図の時. 線対象・点対称 算数問題が解けません。 よくわからないので教えてください。 問題:対象の軸が4本ある図形を選びなさい 正三角形 長方形 ひし形 平行四辺形 台形 正方形 答えは正方形だけなのですが何故ですが ひし形は違うのですか?. 直線に関して対称な点とは、次の図のような関係のことです。 図のように、直線lに関して点Aと点Bが対称であるための条件は ・ ABとlが垂直に交わる ・ ABとlが交わる点PがABの中点である 図に今の条件をかき加えると これらを利用して、次の問題を解いてみましょう。 練習問題 直線"4x−2y+3=0"に関して、点A (−2、4)と対称な点Bの座標を求めなさい まず"4x−2y+3=0"と点"A (−2、4)"を図示.
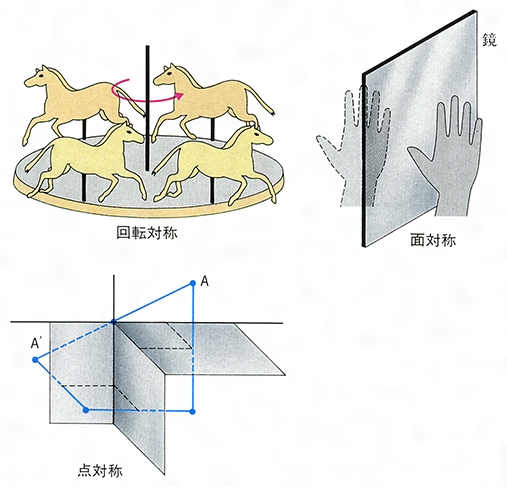
図形の線対称移動 線対称移動とは,ある直線に関して折り返す移動です。 線対称移動の性質として 「対称軸が,対応する点どうしを結んだ線分の垂直二等分線になる」 が挙げられます。 まずは点の対称移動を考えます。. 線対称 (line symmetry/reflective symmetry) 対称軸 (line of symmetry/axis of symmetry)① 点対称 (point symmetry/central symmetry) 対称の中心 ① (point of symmetry/米center of symmetry/ 英centre of symmetry) 回転対称 (rotational symmetry) 回転対象の角 (angles of rotation) 平行移動 (translation) 例文. ①線対称・点対称の意味 ②線対称・点対称の性質 ③線対称・点対称のかき方 ④正多角形と対称な図形の見方 教え方1 折り重ねて重なる形を見せて、重ねたときの重なる点や直線に気づかせながら、線対称の図形を教えます。.
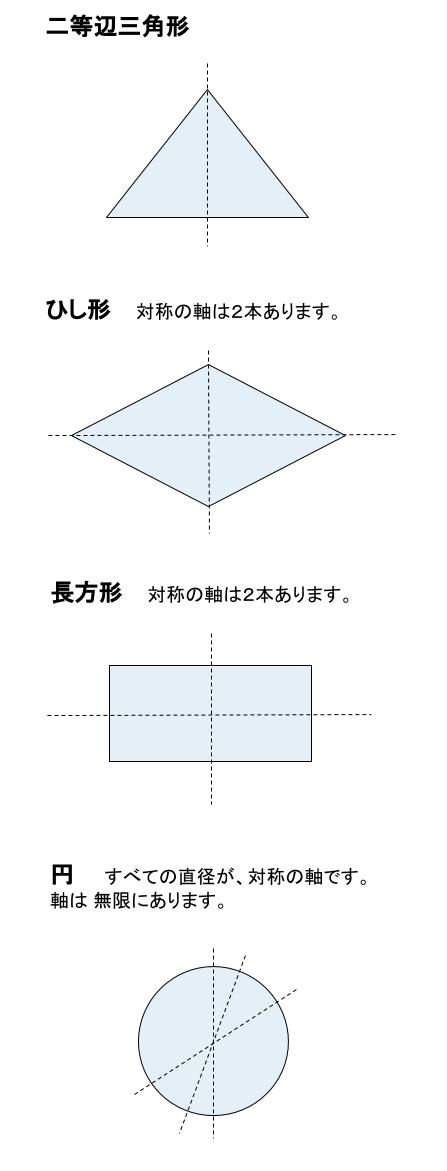
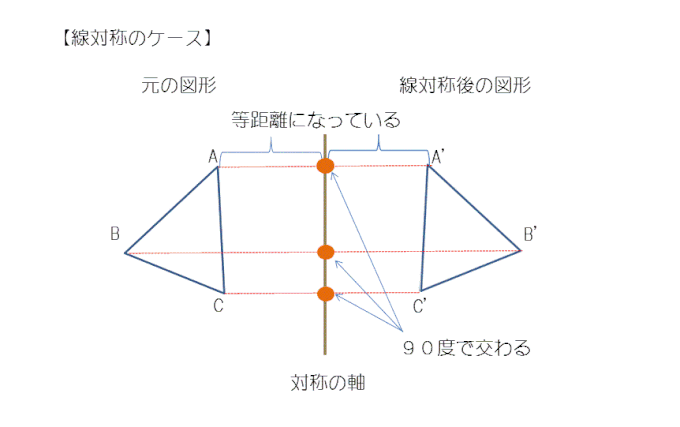
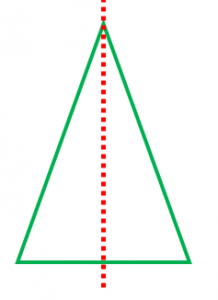
各次元の線対称 線対称の最も一般的な性質は、高次元のものである。 2次元では、それに2次元特有の性質が加わる。 2次元 点線はそれぞれの図形の対称軸を表す。 右下の図形は線対称ではない 2次元図形の線対称は、 反射対称 (英reflection symmetry)と同じものである。 reflection symmetryを線対称と訳すことも多い。 なおその場合、3次元図形のreflection symmetryは面対称と訳す。 対称軸. 技能 線対称、点対称な図形をかくことができる。 知識・理解 線対称、点対称な図形の意味や性質について理解する。 時 学習活動 研究上の手立て 間 ①自分 の内面 とつながり②友達 ③既習事項 1 「線対称な形 」 の特徴 を考① 当たりとし くじ引き 行い、. 線対称と点対称 対称(たいしょう)は、「互いに対応してつりあっていること」を意味しますが、\数学では、 1 1 点 O O を通る直線上で、 O O についてそれぞれ反対の側にあって、 O O から等しい距離にある 2 2 点を、 O O について 互いに対称である と定義しています。 線 対 称 ある直線を折り目として折り返したとき、両側の部分がぴったり重なる状態を 線対称 (せんたいしょう) であるといい.
結晶と対称性 結晶:対称性により分類することができる x線の回折パターンは、結晶の対称性と対 応している →まず、結晶の対称性について理解しよう 対称要素:8種類 単位胞の対称性:32種類 結晶の対称性:230種類 7. 線対称との違いや、基本をおさえていきましょう。 点対称な図形は1点を中心に180度回転させても同じ形 点対称とは、ある1点を中心として図形を180度回転させたとき、元の図形と回転させた図形がピッタリ重なる関係を示します。 たとえば上図の左側にある 図形:正方形ABCDを点Oを中心として180度回転させてみましょう。 すると回転させた前後で全く形が変わらない(右図)のが分かるので. 線・面対称の場合,一方を他の 鏡像 または鏡映ともいう。 (2)一つの図形において,ある対称中心(軸・面)に関しそれと対称な図形が,もとの図形と一致するとき,これを点(線・面)対称な図形という。 また一つの直線(回転軸)を中心として図形を回転させたとき,1/n回転ごとにもとの図形と一致するならば,これをn回回転対称の図形という。 →関連項目 双晶 | 相称 | 対称要素 出典 株.

線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun 数学 正多角形 小学校 算数

中学生の数学講座 線対称 点対称
中1数学 点対称な図形とは まなビタミン
線対称 点対称 のギャラリー

え はなぜ点対称なんですか なぜ線対称じゃないんですか Clearnote
学習プリント Com

私の実践 私の工夫 算数 児童が楽しみながら目をキラキラと輝かせて取り組む授業を目指して 6年 対称な図形 啓林館
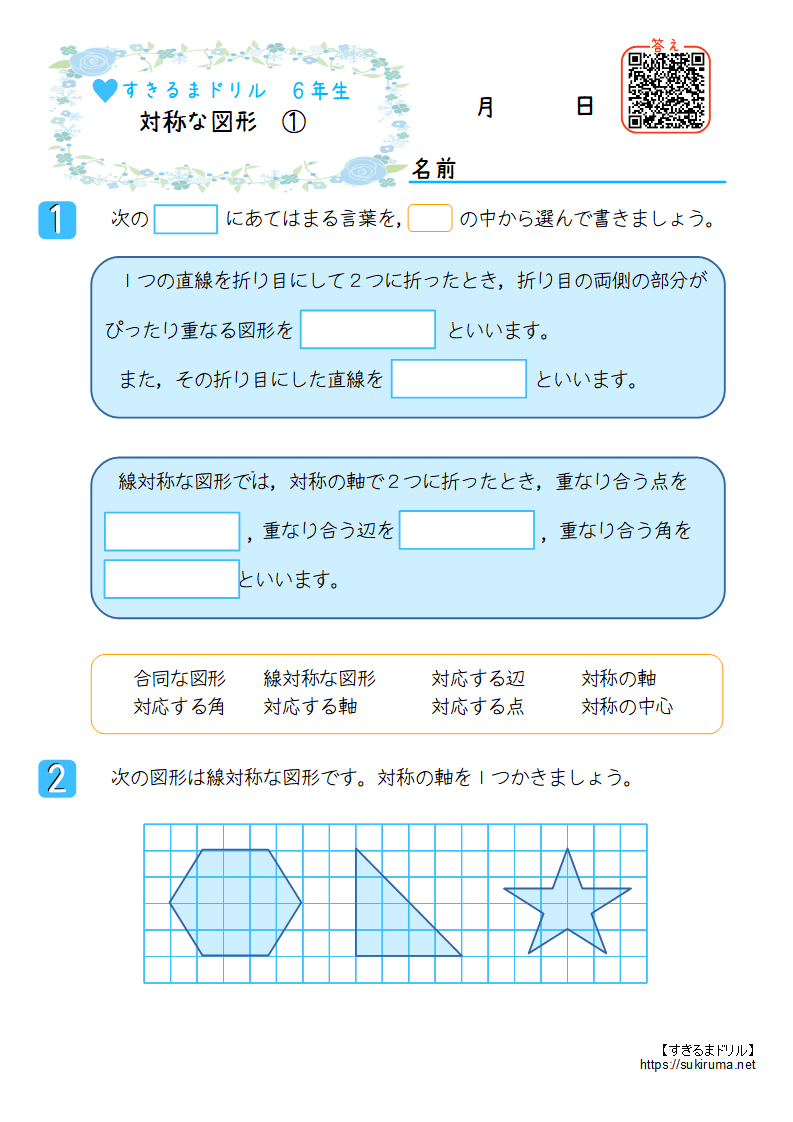
すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント
学習プリント Com
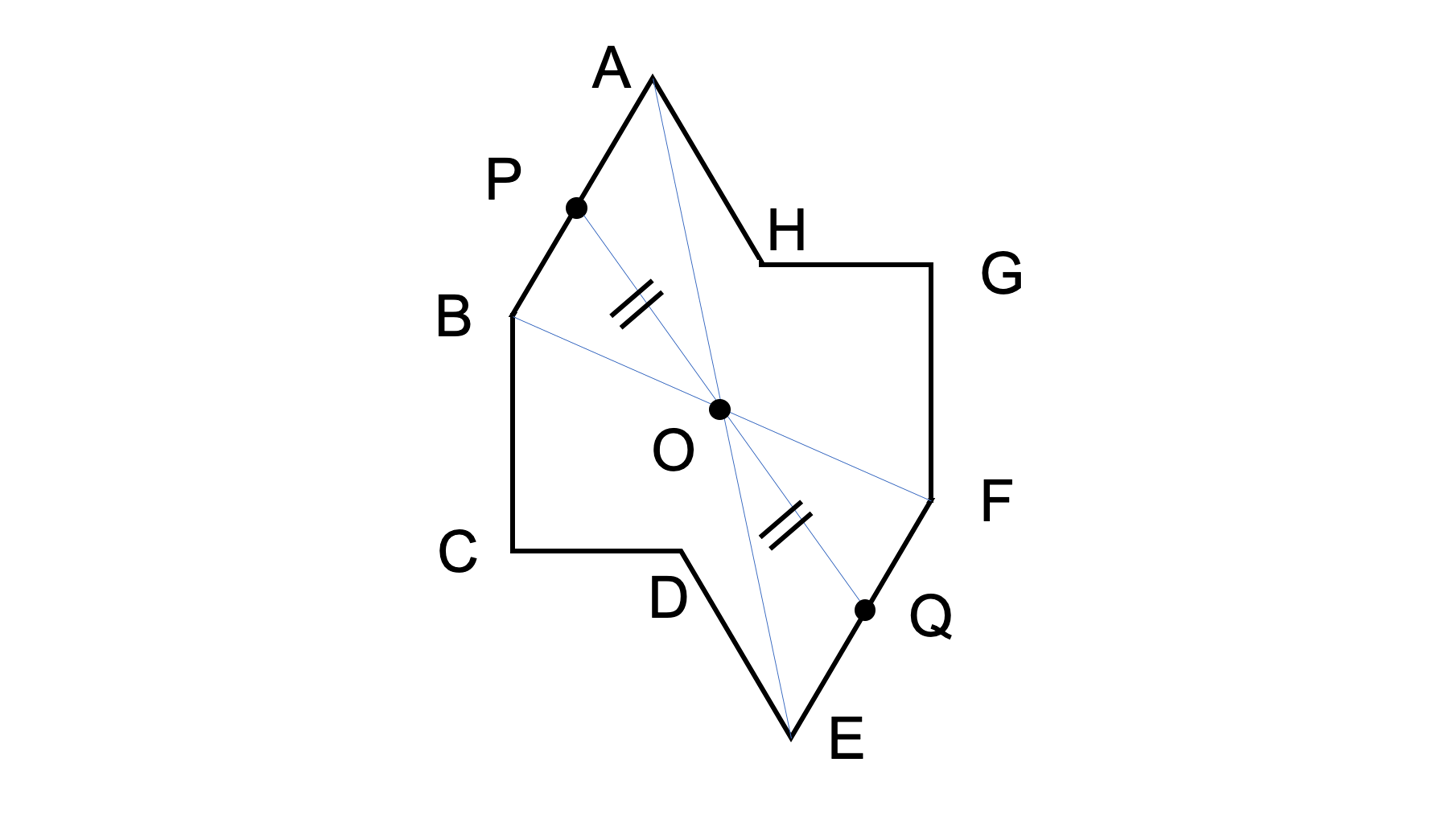
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
多角形と対称 6年生 翁島 おきなしま 小学校ホームページ
このシンボル 県章 は線対称な図形 点対称な図形 ー6年生ー 翁島 おきなしま 小学校ホームページ

線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学
多角形と対称 6年生 翁島 おきなしま 小学校ホームページ

線対称の図形を正確に描けるようになろう 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

三角形の対称性 スクールプレゼンター教材共有サイト スクプレ道場

線対称と点対称1

対称な図形 Ict教材eboard イーボード

6年算数 対称な図形 9時間目 いろいろな図形を対称の見方で調べよう Youtube

対称の授業final 算数

対称な図形 線対称と点対称 小学生 算数のノート Clearnote
小6算数 点対称な図形の性質 指導アイデア みんなの教育技術
中学数学 線対称な図形 中学数学の無料オンライン学習サイトchu Su

線対称図形と点対称図形の見分け方 算数解法の極意
中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su
線対称と点対称の違いを十分理解して混同しないこと 小学生の子供の成績を上げる方法

小六の復習 線対称 点対称な図形 小学生 算数のノート Clearnote

世界一分かりやすい算数 小6 対称な図形
円は点対称 線対称のどちらですか 両方です 円の真ん中を中心と Yahoo 知恵袋
線対称 点対称
線対称 点対称
3
線対称と点対称 小6 再度確認と定着 算数の教え方教えますmother S Math Happy Study Support

小学6年生 算数 8月 線対称 点対称 円の面積 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support
地図記号 これは線対称 点対称 ー6年生ー 翁島 おきなしま 小学校ホームページ
中1数学 点対称な図形とは まなビタミン
Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor
対称とは コトバンク

悩みのタネ 線対称 と 点対称 声に出さないけど思っていること
中1数学 点対称な図形とは まなビタミン
対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学
6年算数線対称点対称図形 わかる教え方
1

6年生 算数 線対称 点対称のテスト かぎやっ子日記
1
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
図形と方程式 直線に関して対称な点について 日々是鍛錬 ひびこれたんれん

対称の英語 線対称 点対象 平行移動など 英語独学マスター
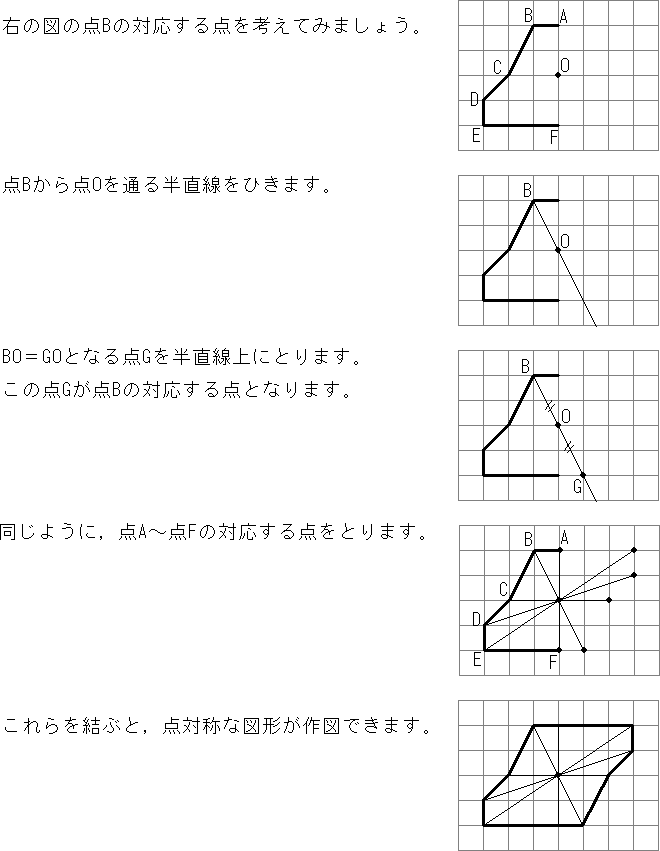
点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト

世界一分かりやすい算数 小6 対称な図形
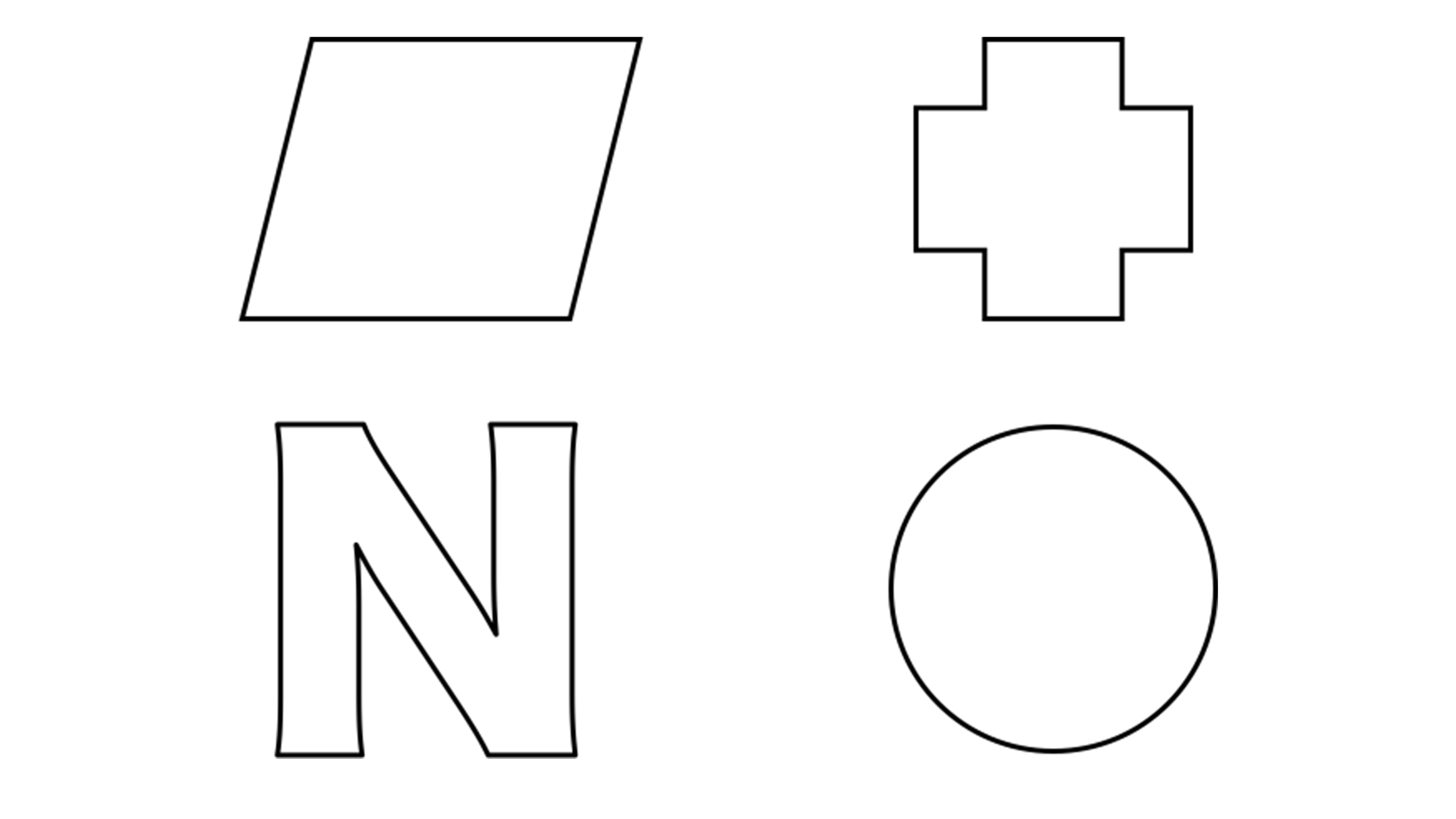
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
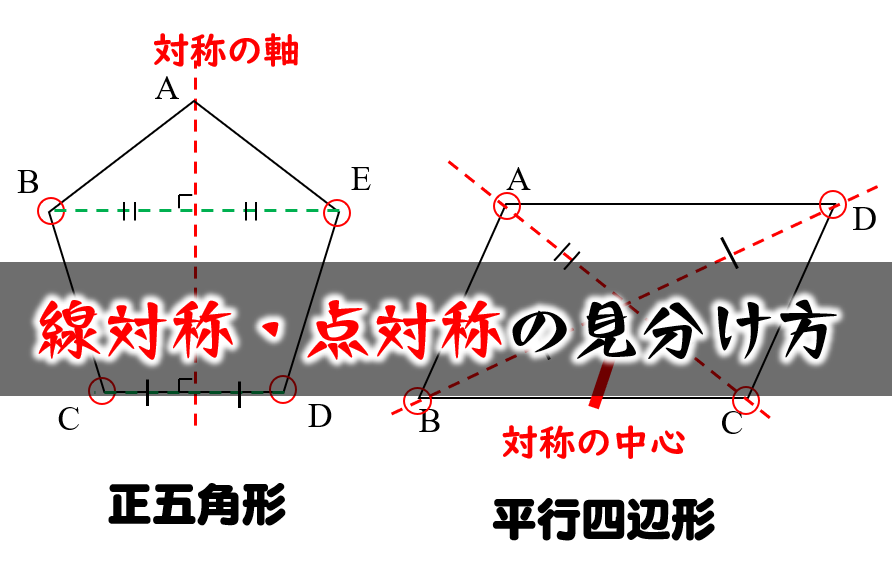
線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun

平面図形 線対称と点対称の覚えておきたい3つの違い Qikeru 学びを楽しくわかりやすく
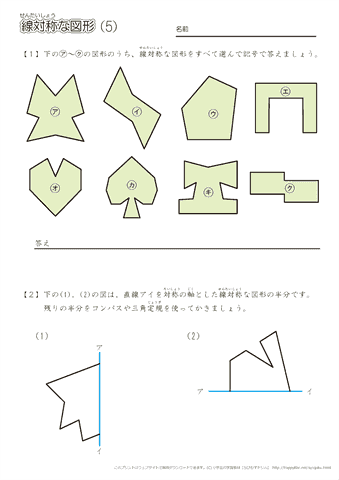
小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生

6年 線対称 点対称 小学生 算数のノート Clearnote
小6算数 対称な図形 点対象 指導アイデア みんなの教育技術
線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
線対称と点対称 小6 再度確認と定着 算数の教え方教えますmother S Math Happy Study Support
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
高校数学 Net
点対称移動

対称な図形 多角形と対称 02 Youtube

スマホok 6年 対称な図形 多角形と対称 Youtube
実践例 プログラミングで対称な図形を学ぶ 山崎智仁 Tomohito Yamazaki Note

線対称 算数解法の極意
点対称とは何 Weblio辞書

線対称と点対称の自主学習ノート 家庭学習レシピ
何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support
線対称と点対称の自主学習ノート 家庭学習レシピ

算数のヒント 1 線対称 豊富小中学校 姫路市立学校園ホームページ

線対称描画と点対称描画について Hyper Paint チュートリアル 使い方 講座
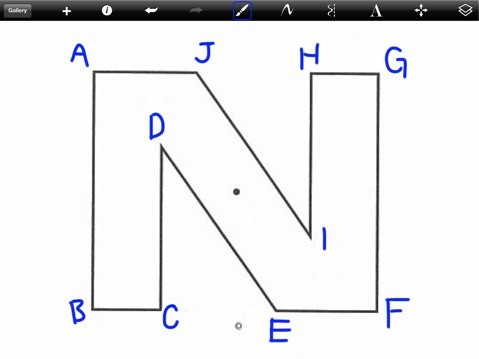
点対称な図形の対応する頂点を確認する Ipadとiphoneで教師の仕事をつくる

線対称 点対称 算数用語集

塾 学校 家庭を結ぶ 受験情報サイト 学びネット

線対称で点対称な図形をかく 算数を究める

小6算数 線対称と点対称の違いは何 線対称と点対称の解き方 教え方 いっしょに勉強しよ

大多喜町 学習支援動画 算数 小学6年生 対称な図形 線対称 点対称 Facebook

小6 対称な図形 四角形 日本語版 Youtube

アルファベットゲームで学ぶ対称図形の取り組み 現場の課題解決策に迫る 授業に役立つヒント お役立ち情報コラム 楽しむ 応募 投稿 教職員共済

小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生

算数のヒント 2 点対称 豊富小中学校 姫路市立学校園ホームページ

算数の単元導入教材 対称な図形 で活用できるアルファベットで対称を探そう 小学校6年生 対称な図形 Youtube
みんなの算数オンライン 教科書レベル 6年 線対称と点対称 多角形の線対称 点対称 例題と解説
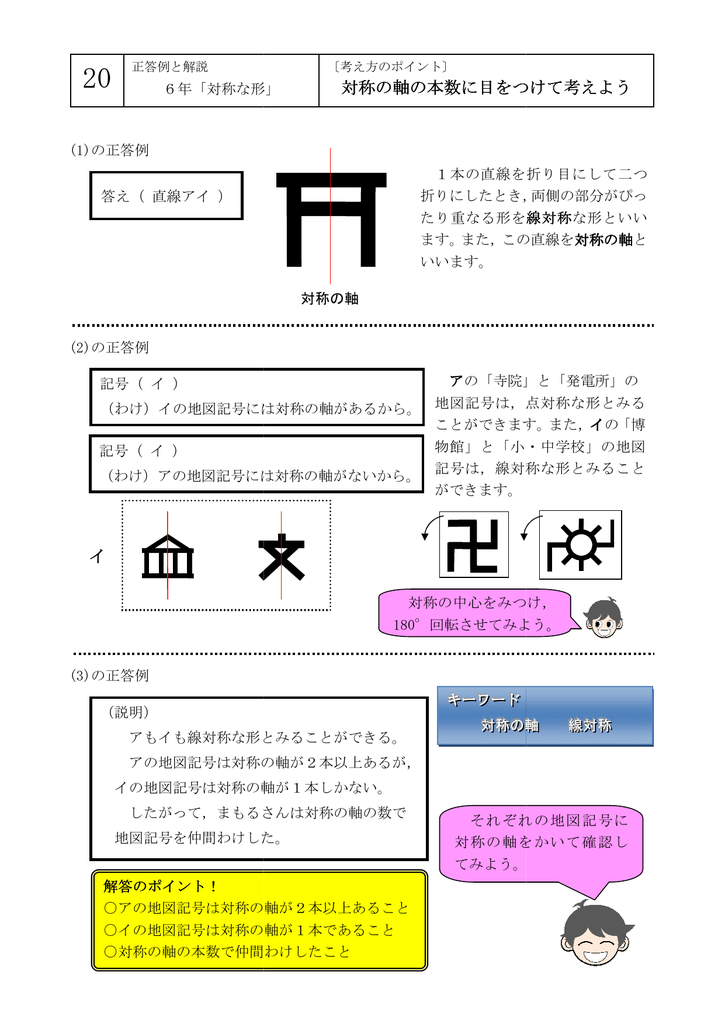
イ 対称の軸の本数に目をつけて考えよ 数に目をつけて考えよう 数に目
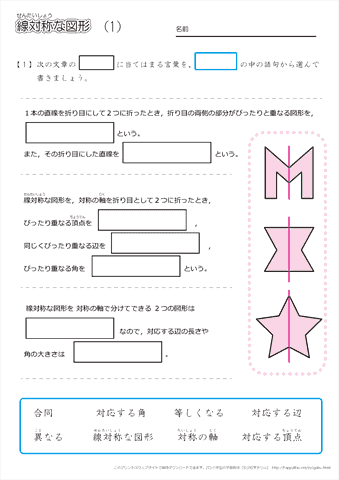
小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生
6年算数線対称点対称図形 わかる教え方
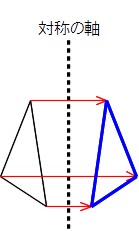
Math 点対称な図形のかき方 働きアリ

線対称と点対称の自主学習ノート 家庭学習レシピ
対称な図形 たしかめよう 6年生 翁島 おきなしま 小学校ホームページ

線対称 点対称 算数用語集

線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
アルファベットのa H R Zの中で 点対称な図形と線対称な図形 線対 Yahoo 知恵袋
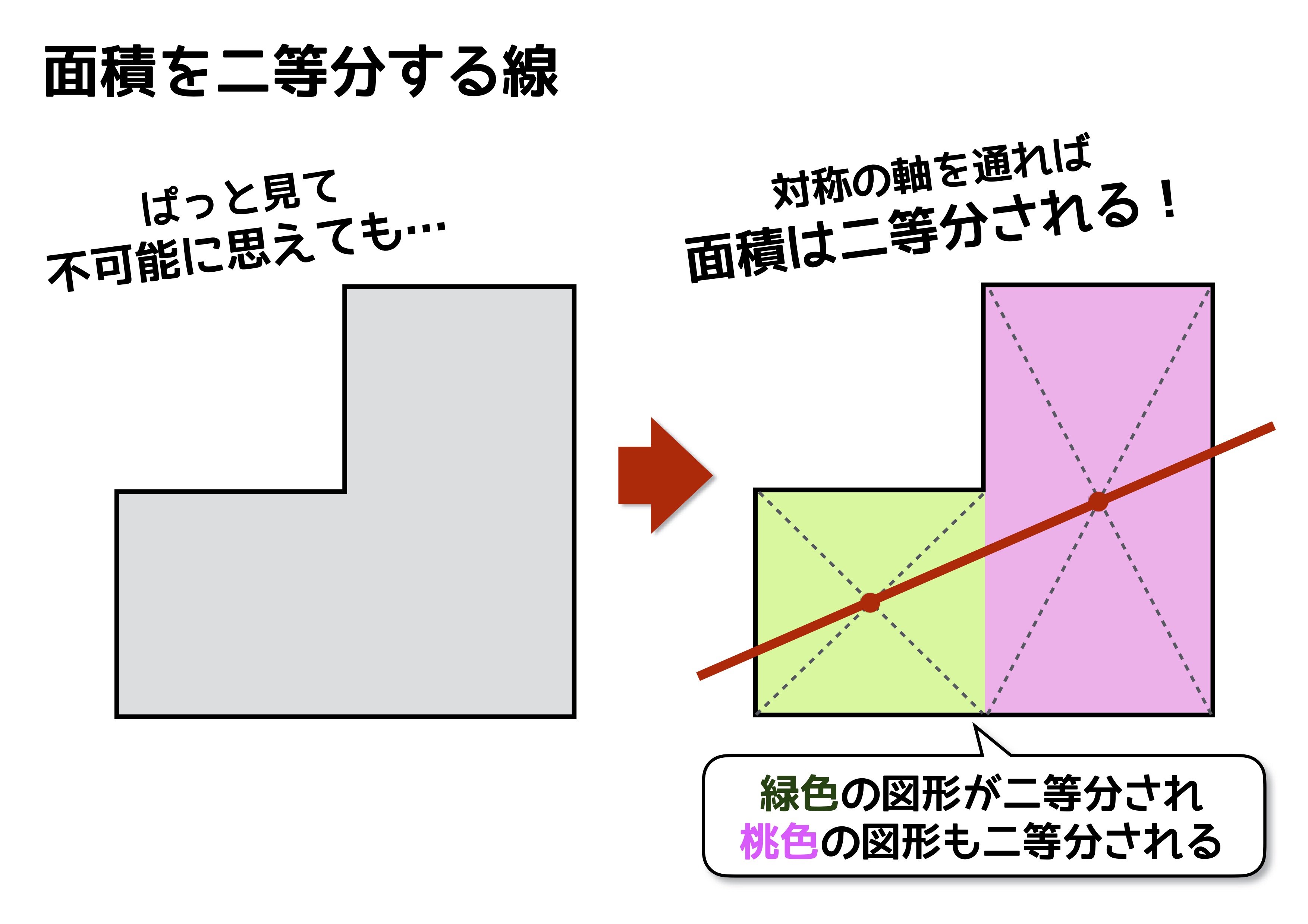
線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
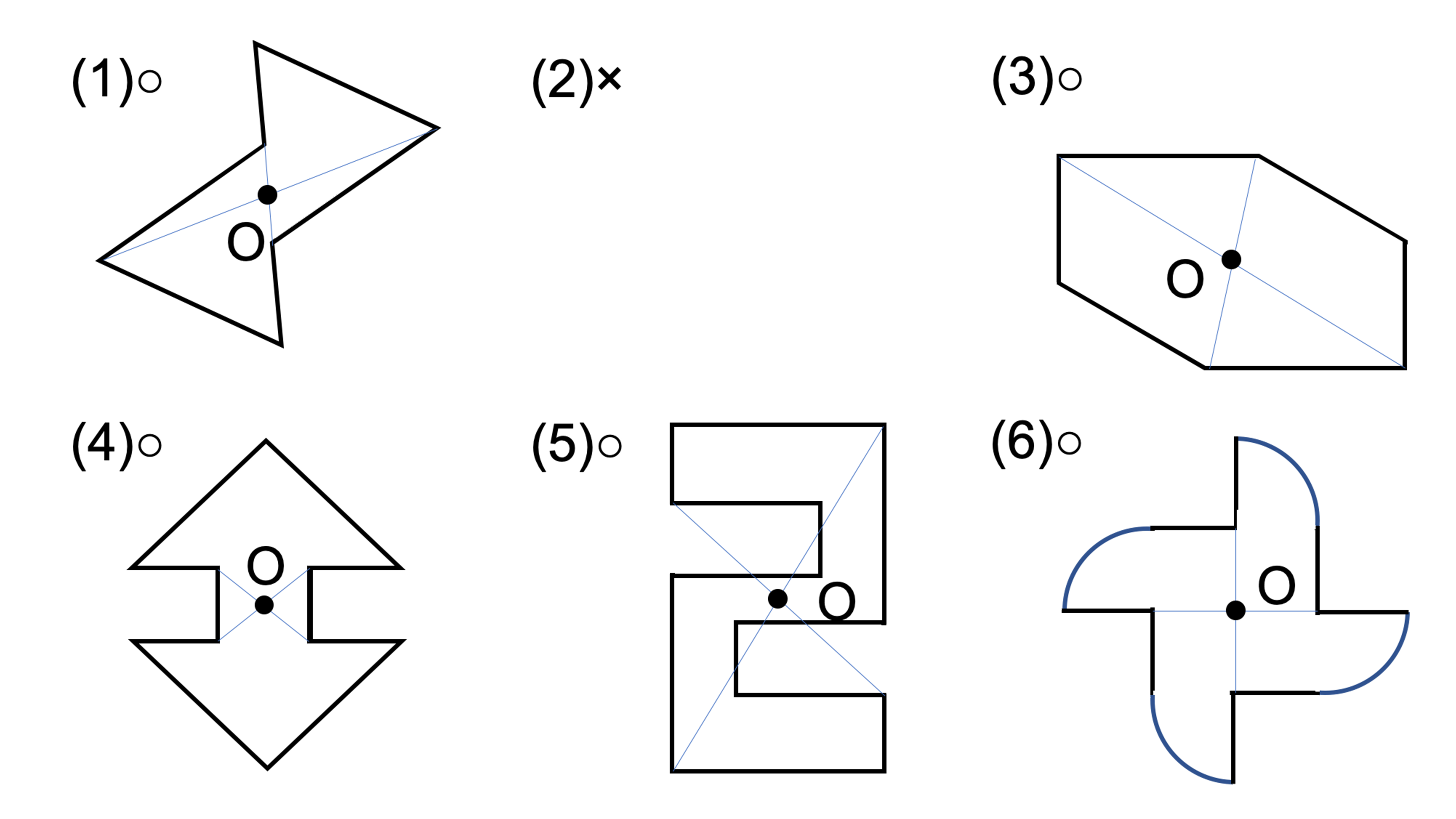
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
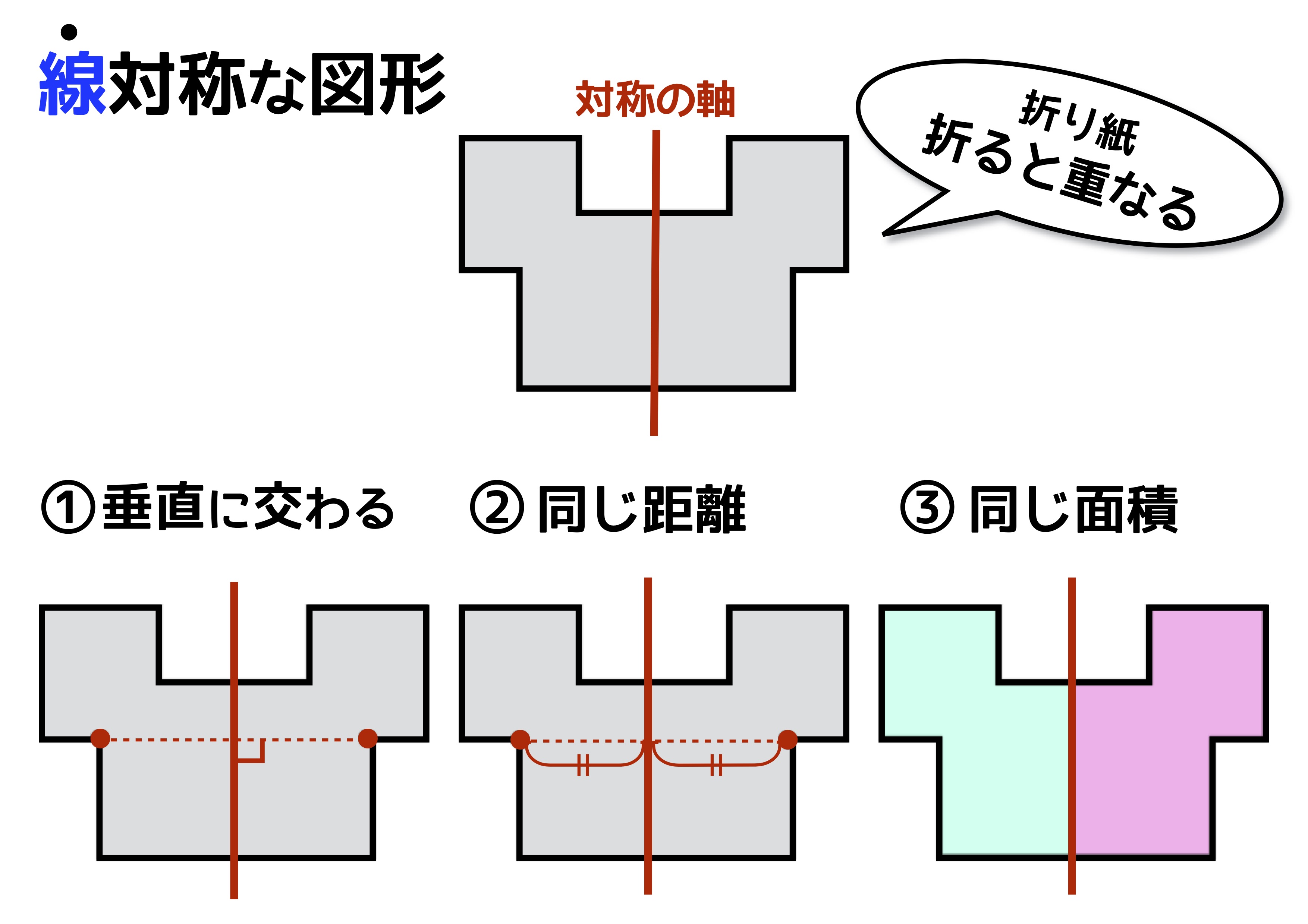
平面図形 線対称と点対称の覚えておきたい3つの違い Qikeru 学びを楽しくわかりやすく

直線に関して対称な点の座標を求める問題 数学ii By ふぇるまー マナペディア

中1数学 円とおうぎ形 について 平面図形 ひっそりと物理や数学を解説する

点対称の図形の書き方を教えてください Clearnote

スタディギア 折って回して考えよう Facebook
線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ

高校入試 英語 数学 学習 線対称と点対称

高校数学 直線に関して対称な点の求め方 練習編 映像授業のtry It トライイット
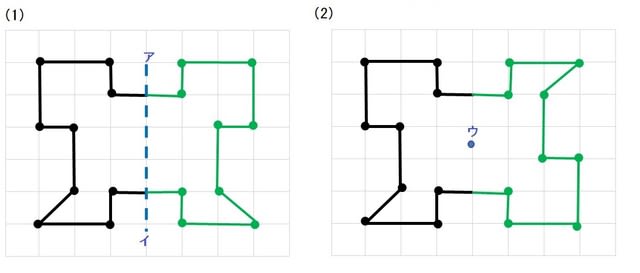
何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




