組み合わせ と 順列
ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。.

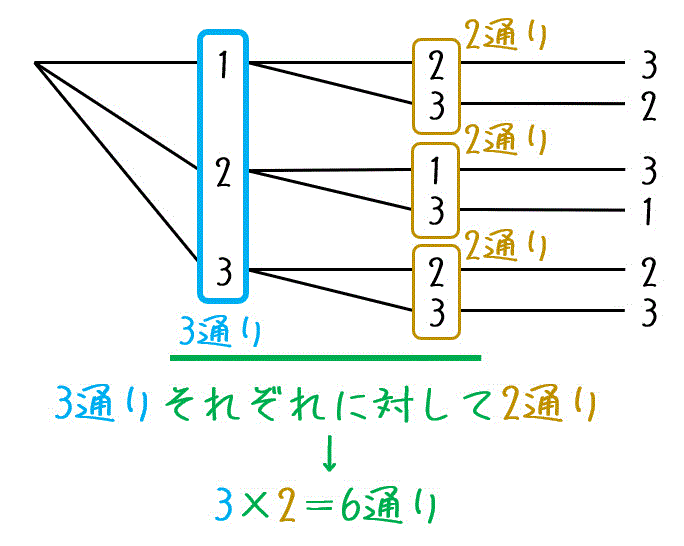
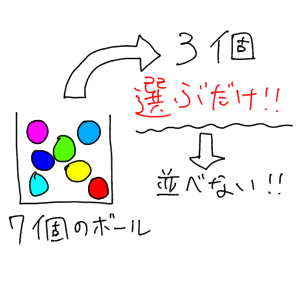
組み合わせ と 順列. 順列では、この 6 パターンを「すべて別の並べ方」としてカウントしますが、 組み合わせでは、この 6 パターンを「 1 つのグループ」としてカウントします。 つまり、この場合の「順列の総数」は「組み合わせの総数」の 6 倍重複しています。 ※ この 6 という数字を「 重複度 」といいます よって「順列の総数」を 6 で割れば「組み合わせの総数」を求めることが可能です。 重複度. 設問1の解答と解説: ここは素直に公式を使うのが確実で一番早い。 順列と組合せの公式がごっちゃにならないように覚えましょう。 設問1は、『走る順番は何通りあるか? 』を問われているので順列の公式を使います。 nは、大人3人と子供4人の合計7人. 順列・組み合わせについては,選んだものが区別できるかどうかで順列か組み合わせかが決まります。 30人のクラスで「 委員長と副委員長1名ずつ 」を決める方法は 順列 で 30 P 2 通り「 2人の委員 」を決める方法は 組み合わせ で 30 C 2 通りでしたね.
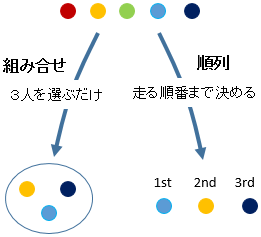
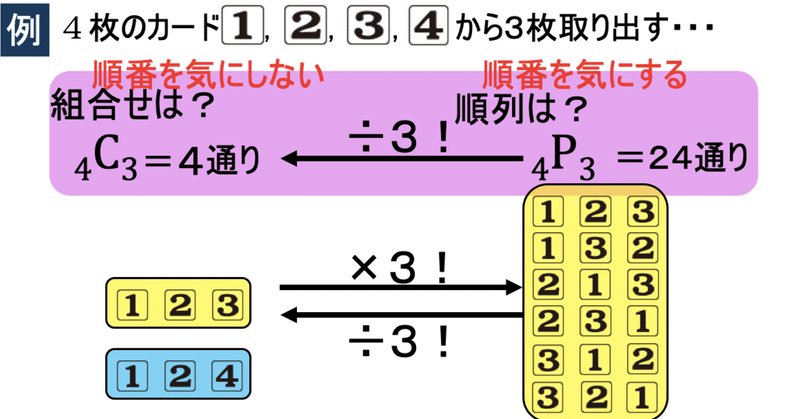
組み合わせとは 組み合わせは順列と混同されがちですが、その内容は大きく違います。それは 並べるのか並べないのか という違いです。どういうことかというと、例えば 5 人から 3 人を選ぶ のと 5 人から 3 人を選んで並べる. 順列と組合せ 順列 (例題) A,B,C,D,E の5枚のカードから3枚取り出し、横1列に並べます。 並べ方は何通りあるでしょう. 順列と組み合わせの使い分けについては, 「 選んだものを区別するかしないか 」 「 選んだものを入れ替えて別の場合になるかどうか 」 で判断できるんだったね。 順列と組み合わせの使い分け 公式の復習最初簡単に思っていても実は難しかったりするのが順列と組み合わせの使い分け方ですね。 順列と組み合わせの公式 順列「 n 個の異なるものから区別できるように r 個を選ぶ方法.
練習問題 順列と組合せの問題を混ぜました。 順列と組合せの違い 順列 :「選んで並べる」「ABとBA を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「ABとBAは区別せず同じもの」 に注意しながら,考えてみてください。 例題3 (1) 5. いろいろな順列 a、b、c、dの4人が丸テーブルに着席する仕方は全部で何通りあるだろうか。 この場合は 図d のように、4人が一つずつ順送りに位置を変えてできる四つの並び方はすべて同じものとみられる。 図d のように、一番上から始めて時計と逆回りにとった四つの順列をabcd, dabc, cdab, bcda. この問題では、 順列と組み合わせ、どちらの公式を使うべき でしょうか。 By frankieleon 正解は、 組み合わせの数の公式 。 答えは 5 C 2 =10通りとなります。 この性質から、組み合わせの数は「コインを5回投げたときに2回表が出る 確率 」を求めるときなどに、 二項分布 の確率関数で利用されています。 コイン投げから分かる二項分布。 正規分布やポアソン分布との関係.
組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する.. 小学6年生の算数 場合の数|組み合わせ 練習問題プリント ツイート 順序は考えず選んで組を作るときの選び方 「組み合わせ」を調べる方法を練習できる問題プリントです。 場合の数・組み合わせ(1) 答え 場合の数・組み合わせ(2) 答え 場合. 順列と組合せ 実は、ここまで学習してきた場合の数は、全て「順列」と呼ばれるものでした。 このページでは「組合せ」について学習していきます。 では、順列と組合せはどこが違うのでしょう。 その違いは一言で言うならば、 順番を気にするかし.
順列のまとめ 6個の異なる文字( a,b,c,d,e,f ) を,重複することなく,3 個順に並べるときの並べ方は全部で何通りあるか? 6P3 6u5u4 通り 10個の異なる文字(a,b,c,d,e,f,g,h,i,j) を,重複することな く,4個順に並べるときの並べ方は全部で何通りあるか?. 確率の順列と組み合わせの問題で 順列 または 組み合わせ -- ---- 組み合わせ 順列 になることはありますか? 高校数学 組分けの問題なのですが、「9人を3人ずつ3組に分ける」という問題で、どうして最後に3!で割るのでしょうか?. 組み合わせは、順序に意味がある順列とは異なります。 総数 = n、抜き取り数 = r とすると、組み合わせの総数は、次の数式で表されます。 問題3それぞれA,B,Cと書かれたカードがあります。.
例として の 3 人が座る場合を考えると,上の図の 3 通りの座り方は, どれも から見て右回りに の順に座っているので同じ座り方になります。 このようなときには円順列の考え方を用います。 まず,誰でもよいので 1 人の座る位置を固定します。. 順列と組み合わせの違いは、選び出した/取り出したものの 並び順を考慮するかどうか です。 「順列」は取り出したものの 並び順を考慮 しますが、「組み合わせ」では 並び順を考慮しません 。 例えば 人 (A , B , C , D , E) の中から 人を選ぶ順列と組み合わせを考えると、人の選び方には A と B、B と C、C と D などがありますね。 「順列」では AB と BA を区別しますが、「組み合. 世界大百科事典 第2版 順列・組合せの用語解説 n個の互いに区別のつくものからr個取って,ある順序に並べたものを順列という。そのような並べ方,すなわちn個のものからr個を取った順列が全部でいくとおりあるかは,で与えられる。また,異なるn個のものからr個を取り出し順序は考え.
1組としたものを、 n 個のものから r 個とった組合せといい、その総数は で求めます。 つまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「. 1 day ago 組み合わせとは「n個の要素からなる集合からk個の要素(元)を重複なし、並び順を考慮しないで取り出して並べたもの」と考えられる。 例えば、「0, 1, 2, 3」という4要素の集合から2個を重複なしで、並び順を考慮せずに取り出そうとすると「 (0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)」という6個の組み合わせがあることが分かる(順列とは異なり、. 順列とは、いくつかのものを順序をつけて列に並べる並べ方の総数です。 組み合わせとは、いくつかの要素の集まりからいくつかの要素を選び出すときの、組み合わせの種類の総数のことを指します。 「順列」も「組み合わせ」もいくつかのものの中からいくつか選ぶというのは共通しています。 しかし、組み合わせは選んで終わりなのに対し、順列は選んだあとの 順番 も決める必.
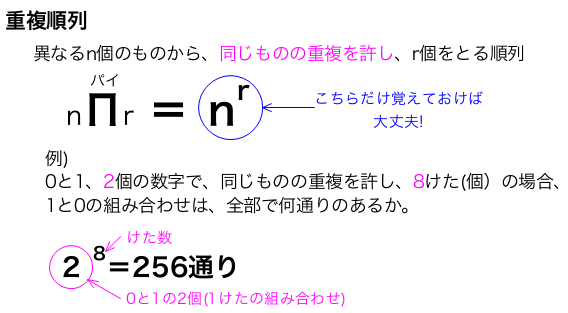
順列と組み合わせ この問題の解説をお願いします 数学 組み合わせの質問です 男子5人女子4人の中から5人選ぶとき少なくとも女子2人が選ばれる組み合わせを求めよ 女子2人を選ぶ組み合わせ4C2 男子と残った女子から3人選ぶ組み合わせ7C3 よって4C2×7C3を答え. 数学的な考え方 順列や組み合わせについて、落ちや重なりのないように図や表を適切に用いたり、名称を記号化して端的 に表したりして、順序良く筋道立てて考えることができる。 技能 順列や組み合わせについて、落ちや重なりのないように、起こり得る場合を順序よく整理して調べること ができる。 知識・理解 順列や組み合わせについて、落ちや重なりのないように調べるには、あ. 組み合わせ論とは、複数の要素が取りえる方法について考えることです。 順列(階乗)重複順列順列組み合わせ についてまとめています。 関連記事:確率期待値と確率頻度分布について 順列(階乗) 順列(階乗)は、ある数の要素を並べるときの数を示.
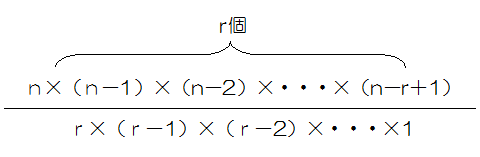
場合の数 組み合わせ 中学受験 田中貴 Com

順列と組み合わせ Alis

重複順列と重複組み合わせの問題はどうやって見分ければいいですか Clearnote
組み合わせ と 順列 のギャラリー
重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78

数学a 順列と組合せの使い分けとコツ 教科書より詳しい高校数学

場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート

なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん
うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾

順列 組合せと確率 新装版 数学入門シリーズ 山本 幸一 本 通販 Amazon

二項定理 二項定理のための 順列 組合せ 大人が学び直す数学

二項定理 二項定理のための 順列 組合せ 大人が学び直す数学

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

Excelを使った数値計算ツールsuitexl

Python 順列 組み合わせを求めよう Python初心者の備忘録
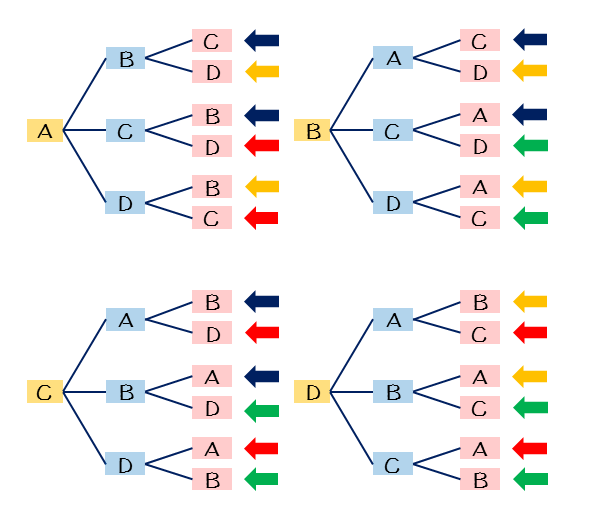
順列と組み合わせの違いをリレーのチーム選考に例える コード7区

順列と組み合わせ 算数用語集
数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki

順列と組合せの違いやイメージを徹底解説 問題のパターンや解き方のコツまで伝授 文系受験数学ラボ
組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ

高校数学a Npr と Ncr の使い分け 映像授業のtry It トライイット

順列と組み合わせの公式とその違い 問題付き 理系ラボ
円順列 公式

重複順列と重複組合せ 感じる科学 味わう数学

順列と組み合わせの関係 楽しく学ぶ大学受験数学

場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ

重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

順列の問題 一定の条件で並べる 高校数学の知識庫

順列組合せの公式はp 総乗 を使うべき 万象酔歩
組合せの計算の導入 順列との違い Root Note

順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典

Android 用の 順列 組み合わせ Apk をダウンロード

同じものを含む順列の問題 京極一樹の数学塾

場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ

順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング

場合の数 組合せについて 日々是鍛錬 ひびこれたんれん
場合の数 組合せについて 日々是鍛錬 ひびこれたんれん
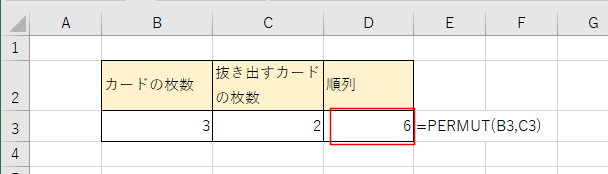
順列と組み合わせを計算する Permut Combin関数 Excel関数

重複順列と重複を許して取る組み合わせの違い Clearnote

高1 数a 場合の数 4 組合せ 高校生 数学のノート Clearnote

順列pと組み合わせcの違いと 簡単 な見分け方
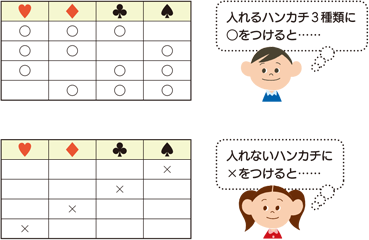
順列と組み合わせ 算数用語集
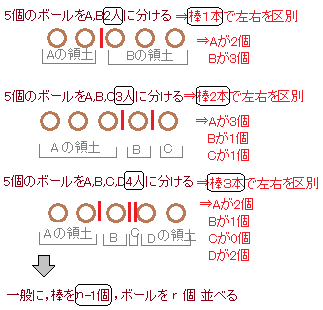
重複組合せ

順列 組合せ記号 Pukiwiki
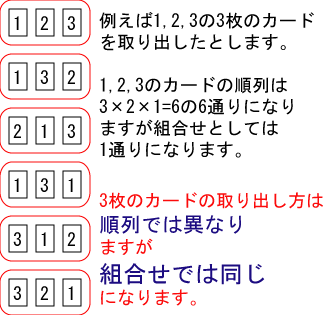
組合せの総数

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
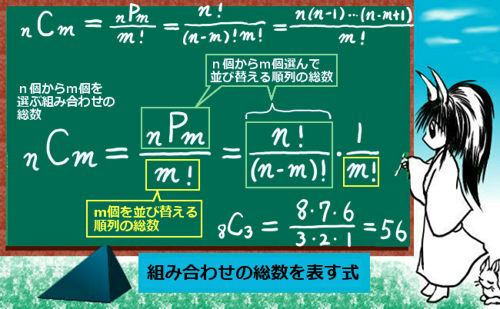
組み合わせの総数 場合の数 理数系無料オンライン学習 Kori

Excel Permut関数 順列の数を求めたい くうねるのエクセル教科書
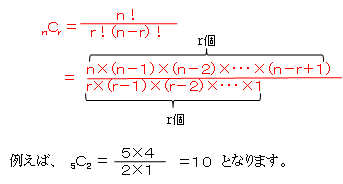
順列 組合せ 確率 統計 web教材 木暮

高校数学 数a 15 組合せ 文字編 Youtube
数列 順列 組み合わせ計算機 1 0 2 Apk Download Com Easelabs Software Progressioncalculator Apk Free

動画で解説 数学講座 順列と組み合わせのちがい ふじい塾 English Mathematics

重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学

数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki

順列 組合せランダムチェック公開 現役講師が作った使えるサイト

リンゴ9個 重複組合せ 解説その1 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
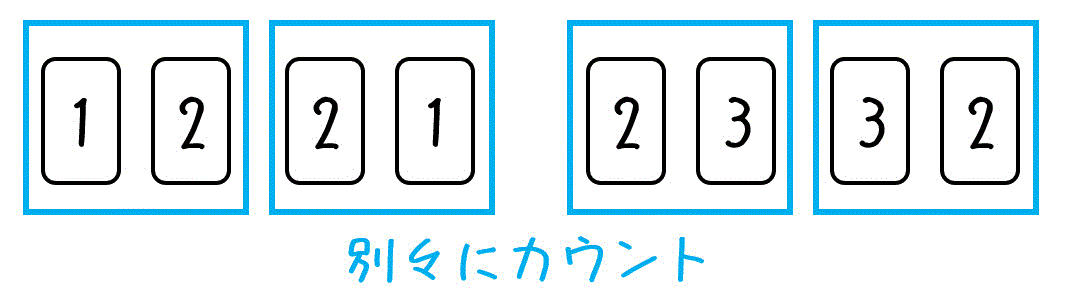
うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾

算数における順列 組み合わせの扱いについて かけ算の順序の昔話
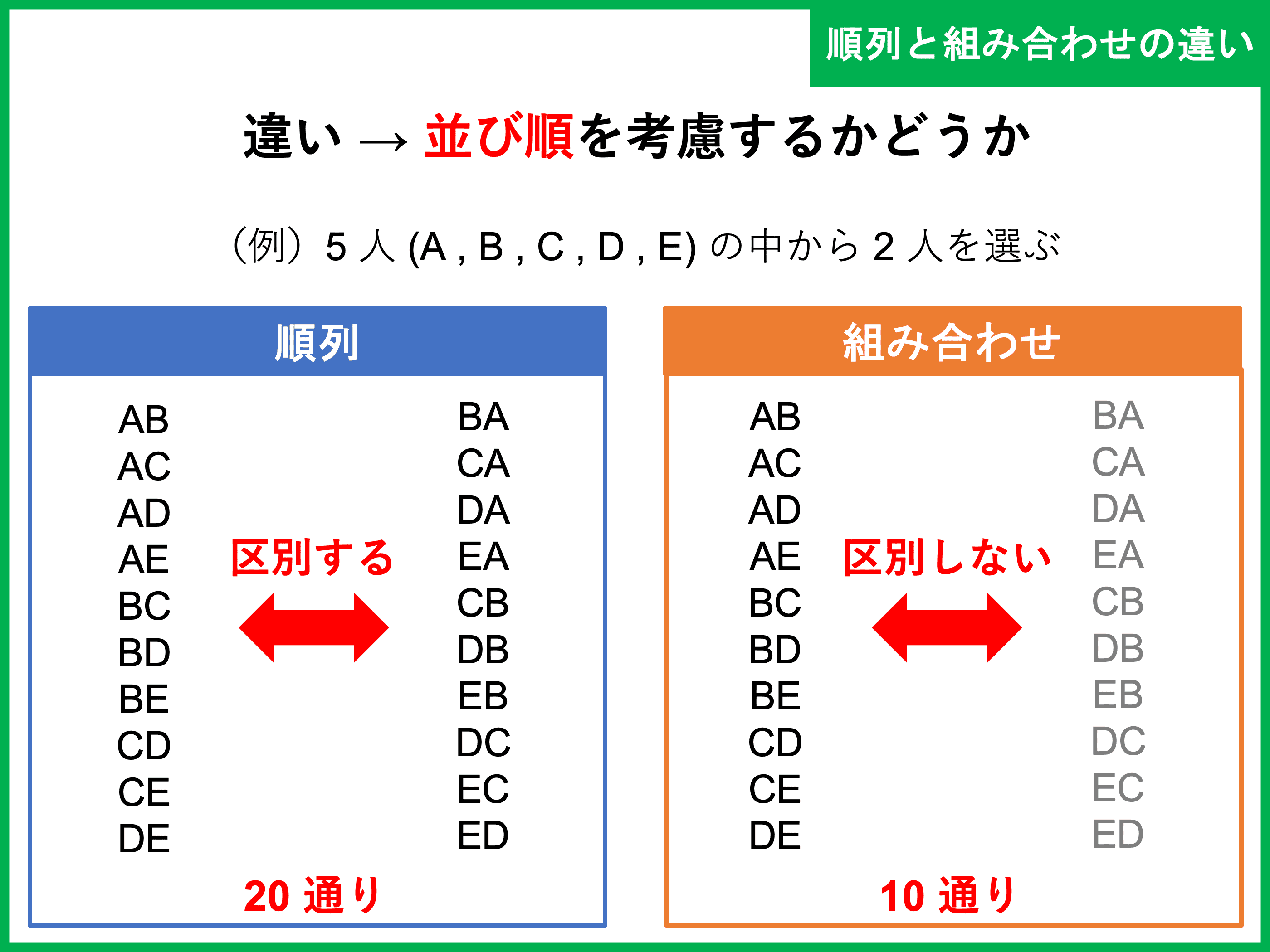
順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典
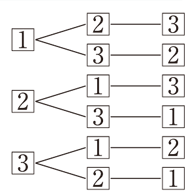
順列と組み合わせ 算数用語集

順列と組み合わせの公式とその違い 問題付き 理系ラボ

順列 組合せの覚書
数列 順列 組み合わせ計算機 Para Android Baixar Gratis Versao Mais Recente 21

順列と組合せの違いと例題 高校数学の美しい物語

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
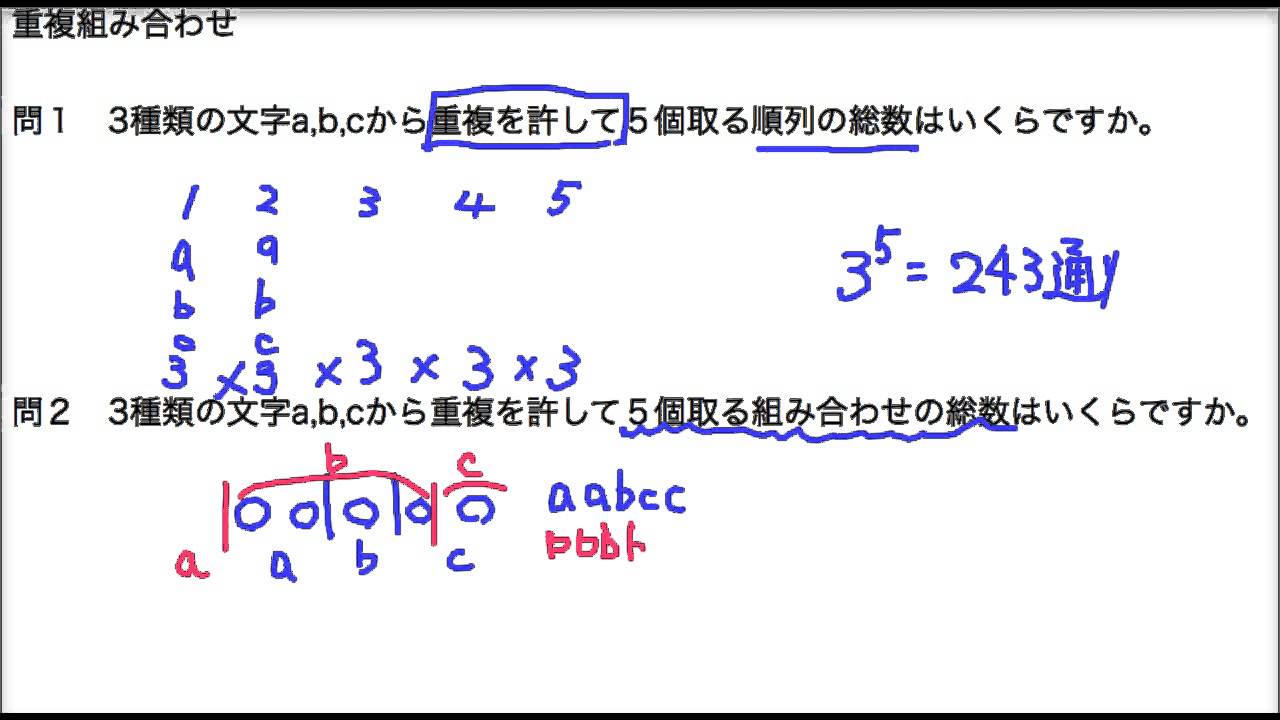
重複組み合わせ1 順列と組み合わせの違い Youtube

順列と組み合わせの公式とその違い 問題付き 理系ラボ
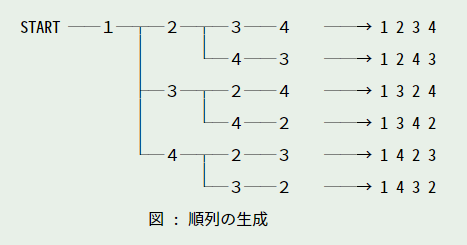
お気楽 Scheme プログラミング入門

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ

同じものを含む順列の問題 京極一樹の数学塾

3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ

順列と組み合わせの公式とその違い 問題付き 理系ラボ

数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube

1日1題spi 順列 組み合わせ サプログ 企業の人事 大学の教授 職員 社会人 内定者との協力体制を整え 就活生 そして働くことを頑張りたい人を応援します

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ

組み合わせの総数ncrを求めよう だいたい1分でわかる ネコのて動画 マナビジョン Benesseの大学 短期大学 専門学校の受験 進学情報
Spi練習問題 Com

Pythonで階乗 順列 組み合わせを計算 生成 Note Nkmk Me
Spi練習問題 Com

順列と組み合わせの公式とその違い 問題付き 理系ラボ

同じものを含む順列と組合せは 同じ です 問題4選もあわせて解説 遊ぶ数学

最短経路 順列 優技録
Spi練習問題 Com

北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭
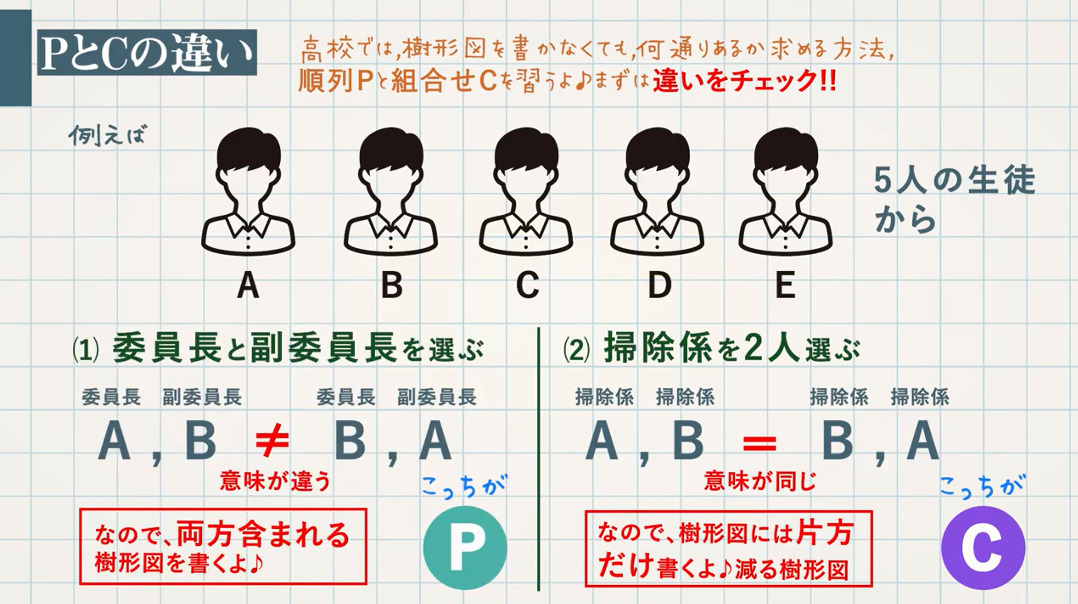
場合の数 番外編 順列p 組合せc 教遊者

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

順列と組み合わせの公式とその違い 問題付き 理系ラボ
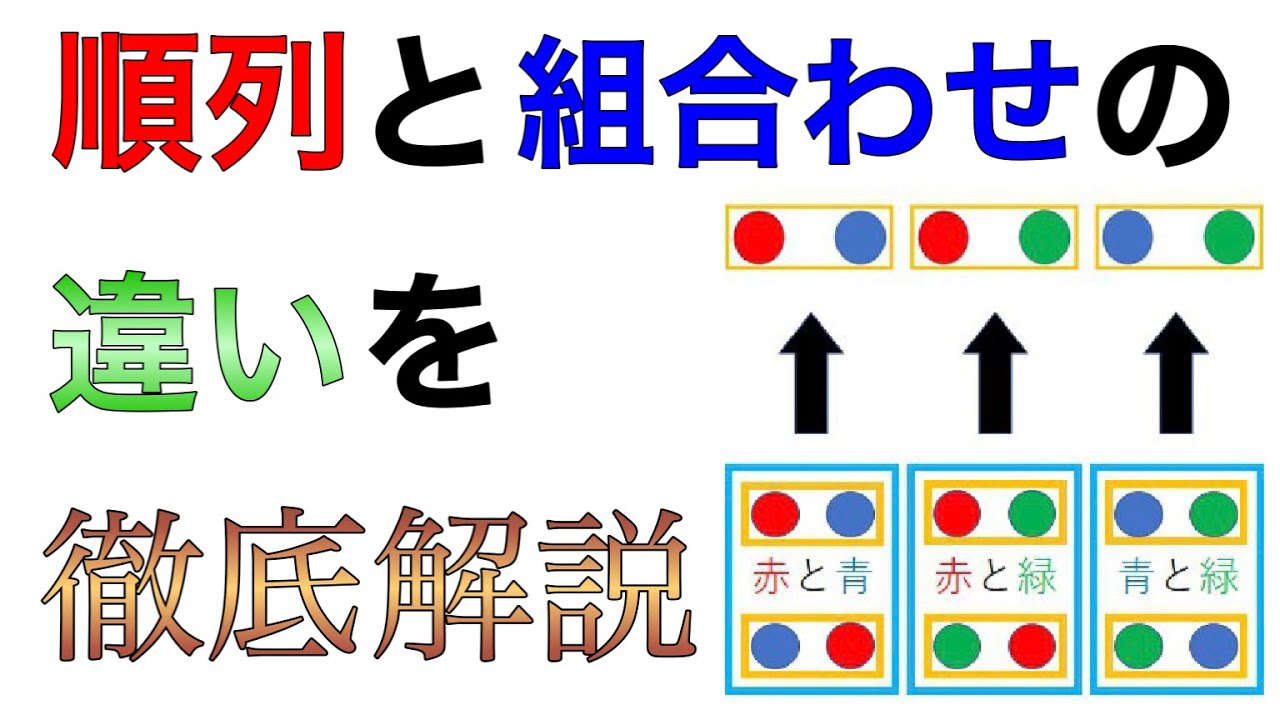
順列と組み合わせの違いを基礎からわかりやすく解説 Youtube

Spi 数学 対策問題 組み合わせ 順列 しかくのいろは

苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業

機械学習の統計学 順列と組み合わせって何 ししまる みらいのクルマをつくる人 Note

高1 数学a 順列 組み合わせ 高校生 数学のノート Clearnote

重複順列と重複を許して取る組み合わせの違い Clearnote

組み合わせ なぜ階乗で割るのかイメージ解説しました 中学数学 高校数学のサイト ときどき大学数学
1
3

順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
1

順列と組み合わせの違いとは そしてそれぞれの意味を0から解説

中学数学 場合の数
練習問題2で なぜこの問題は組み合わせの公式ではなく 順列の公式を使 Yahoo 知恵袋
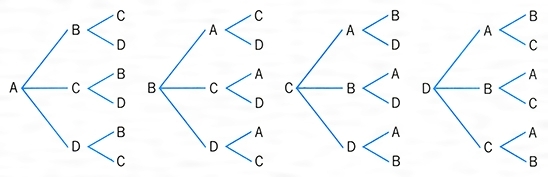
順列 組合せとは コトバンク

数列 順列 組み合わせ計算機 By Yoshiaki Onishi




