三 平方 の 定理 応用
70以上 三 平方 の 定理 応用 余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 一般に、交流回路の計算では、瞬時値の代わりにベクトルを用いる。 ベクトルは原点を起点とした大きさと偏角を持つ量.
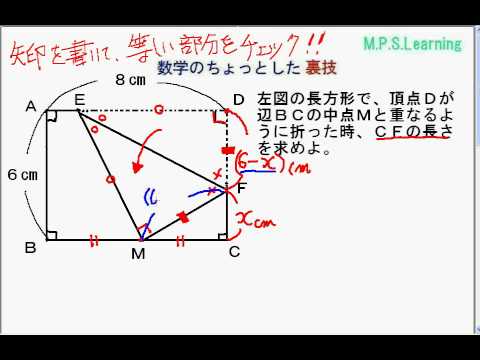
三 平方 の 定理 応用. ですから, 余弦定理の場合は − 2 b c cos θ の項が三平方の定理に付け加えられているだけですね. つまり, ∠ A が 90 ∘ から θ に変わると,三平方の定理の等式が − 2 b c cos θ 分だけズレるということになっているわけです. このように見る. 三平方応用 折り返し 例題 長方形ABCDの頂点CをAと 重なるように折り返すときの 折り目FGの長さを求める。 A B C D E F G 12cm 18cm 直角三角形ABGで三平方の定理を用いてAGとBGを求める。 AG=xcmとする。 AGはCGを折り返した線分なのでBG= (18x)cmとなる。 三平方の定理より 122 (18x)2=x2 144 xx2=x2 36x = 468 x = 13 A B C D E F G 12cm 18cm P 13cm 5cm. 四平方の定理とはひとことでいうと三平方の定理の3次元空間バージョンです. そう,四平方の定理はかの有名な三平方の定理さんと親戚のような関係なんです笑. 三平方の定理だと, $${ a }^{ 2 }{ b }^{ 2 }={ c }^{ 2 }$$ ですが四平方の定理だと,.
こんにちは、ウチダです。 今日は、数学Ⅱで習う 「剰余の定理と因数定理」 について、まずは剰余の定理をわかりやすく証明し、実際にどう用いて問題を解いていけばよいかを考察し、最終的には二乗で割った余りを求める応用問題なども解説していきます♪. A B C ABC ABC の面積を表します。 三平方の定理の三次元空間バージョンです! なお,四平方の定理というと整数論におけるラグランジュの四平方和定理( →整数論の美しい定理7つ の5つ目)のことを指す場合もあるので注意して下さい。 目次 四平方の. ・直角三角形 ⇒ ならば (斜辺c)2 = (隣辺a)2 (対辺b)2 ・ (最大の辺) 2 = (他の辺) 2 (他の辺)2 ⇒ ならば 直角三角形 cf 直角三角形の辺の名前 ∠θを基準に、 隣にあるのが 隣辺 対面にあるのが 対辺 ですが中学では、「斜辺」と「それ以外」で十分ですね これだけです! 直角三角形 の3辺のうち、 2辺が判れば残りの1辺がわ.
三平方の定理とは、別名「ピタゴラスの定理」とも呼ばれる、とても古くからある数学の定理です。 具体的にはCを直角とする直角三角形ABCの辺 a,b,c a, b, c について、 a2 b2 = c2 a 2 b 2 = c 2 が成り立つ、というものです。 この定理は紀元前1800年ごろにまで遡ることができ、当時のバビロニア粘土板に描かれている数がこの三平方の定理のことを指しているのでは、という研. 四平方の定理 ~三平方の定理の拡張~四平方の定理三平方の定理というと, 直角三角形において,(斜辺の2乗) = (他の2辺の2乗の和)が成り立つという有名な定理ですここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四三 平方 の 定理 三平方の定理 中 3 数学 三. 三 平方 の 定理 応用 問題例題1 下の図の、\\ (x\\) の値を求めなさい。 解答 下の図のように補助線をひき、左の直角三角形に 三平方の定理を用います。 \\ (x^2=2^28^2\\) \\ (x^2=68\\) \\ (x=±\\sqrt {68}\\) \\ (=±2\\sqrt {17}\\) この問題では、当然 \\ (x\\) は正の値なので.
して,三平方の定理を利用 し,問題を解決することが できると実感している。 〔ICEモデル〕 角三角形の辺の長さを求め の具体的 考え・基礎知識 応用・ひろがり 三平方の定理を理解し,直 ることができる。 三平方の定理を使えば,線. 三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角. まずは、ピタゴラスの定理(三平方の定理)をおさらい ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。 直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c² 例えば、斜辺5cm、底辺3cmの直角三角形の場合、以下のようにもう1辺の.
三 平方 の 定理 空間 図形 難問この映像授業では「中3 数学 三平方の定理6 空間図形」が約8分で学べます。 問題を解くポイントは「立体の対角線や高さは、三平方の定理をADqは∠D=90゜の直角三角形.また,dqは三平方の定理により4√2 だから、 adqに三平. 三平方の定理は、数百通りともいわれる証明法が提案されている。 よく目にする証明法は、正方形を用いた証明、相似を用いた証明、内接円を用いた証明などがあります。 三平方の定理の一般角への応用 三平穂の定理は、あくまでも直角三角形において成り立つ定理ですが、一般角においてはどうなるのでしょうか。 それは、高校数学で学ぶ、第二余弦定理というもので、以下のように表されます. 三平方の定理 kaztastudy 中1作図直角90度を三等分する線の書き方を解説! 二次方程式平方根の考えを使った解き方、平方完成を利用した解き方を解説!.
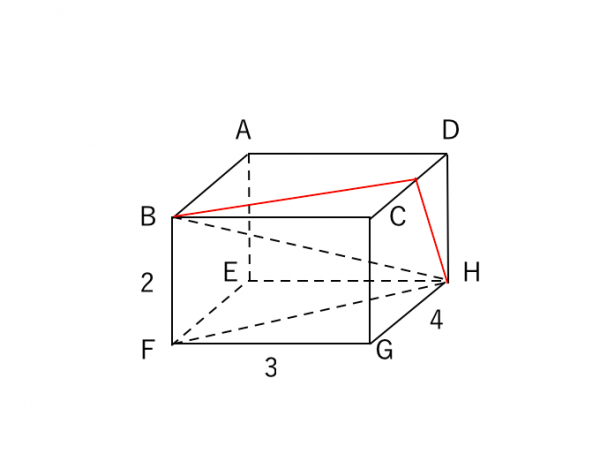
三平方の定理の応用問題 応用問題①「1 辺と 1 角から辺の長さを求める」 応用問題②「2 辺の長さを求める」 三平方の定理とは? 公式 三平方の定理とは、 直角三角形の辺の長さについて成り立つ等式 です。 まずは定理を確認してみましょう。 三平方の定理 直角三角形の直角を挟む 辺の長さを とし、斜辺を とすると、 の等式が成り立つ。 文字だけだとわかりづらいですが、以下. 三平方の定理を利用することができます。 すると、それぞれ と表すことができます。 この2つの式を連立方程式とみて計算すると が等しいので、代入法で解くと の値がわかったところで に代入してやると だから このようにして 三角形の高さを求めることができました。 よって、三角形の面積は 答え 高さがわからない三角形では このように直角三角形を2つ作り それぞれの底辺を を用いて表す。 そ. 三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 立体は切断したり、展開したりしてできる限り平面で考える 直方体の対角線 例 対角線の長さBHを求める。 A B C D E F G H 5cm 4cm 3cm 方針 対角線BHを斜辺とする直角三角形は BFHだが、 辺FHの長さが出ていない。 そこで先に直角三角形FGHで三平方の.
2平方定理 この定理はフェルマーの2平方定理とも呼ばれることがあり,証明はオイラーによってはじめてなされたとされています. 定理. 奇素数 (奇数かつ素数,すなわち 3 以上の素数) p p が 4 で割ると 1 余るとき, p p は 2 つの平方数の和として表さ. 数学中学三年生三平方の定理の応用の問題です。 問題文図は、幅4cmの紙テープを線分ACを折り目として折ったものである。∠ABC=30度のとき、次の問いに答えよ。1.線分ACの長さを求めなさい2.線分BCの長さを求めなさい3.網の重なった部分 ABCの面積を求めなさい※特に2がわかりません ABCでAC. こんにちは!レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 見た目はシンプルで一見簡単そうに見えますが、かなりの難易度だと思います。 さすが灘 (*´Д`) ヒント 答え 詳しい解説 ①補助線を引く ②ABの長さを求める ②1 相似を見つける ②2 DE EA = BD BA ③三平方.
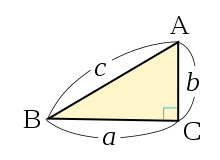
三平方の定理 右図のような直角三角形については b2c2=a2 が成り立つ. 三平方の定理を使えば,直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる. たとえば右図では, b , c が分かっていれば a が求められる. a , c が分かっていれば b が求められる. a , b が分かっていれば c が求められる. 例1 右図で黄色の三角形について三平方の定理を使うとAHの長さが求めることがで. 三平方の定理のポイント 三平方の定理はピタゴラスの定理ともいわれ有名な定理ですが、 中学校では図形の最後に習います。 応用範囲は広いです。 しかし、1,2年生のときにしっかり基本を身につけていれば大丈夫です。. が成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。.
三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 A B 例図の線分ABの長さを求める。 x y O A (2,1) B (7,3) 確認線分ABの長さを求めよ。 A (1,5) B (6,2) x y O B (2,2) A (1, 4) O x y 長方形. ・空間図形のなかに,三 平方の定理を利用する ための直角三角形を見 いだすことができる. ・三平方の定理やこれま でに学んだ図形の性質 を利用して,問題を解 決することができる. ・三平方の定理を利用し て,直角三角形の辺の長 さを求めることが. 三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて.
ピタゴラスは遅かった 三平方の定理「最古の応用例」 畑の図面が記されている粘土板。 三平方の定理を使って面積や形が正確に描かれている. この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだ。 たとえば、斜辺の長さがc、その他の辺の長さがa・bの直角三角形ABCがあっとすると、 a² b² = c² っていう公式が成り立っているんだ. ① 三平方の定理 三平方の定理 (ピタゴラスの定理) c2= a2 b2 これだけです !!.
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と.
中学数学 三平方の定理を利用した応用問題の解き方のコツを教えてください Yahoo 知恵袋

三平方の定理の応用

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
三 平方 の 定理 応用 のギャラリー

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
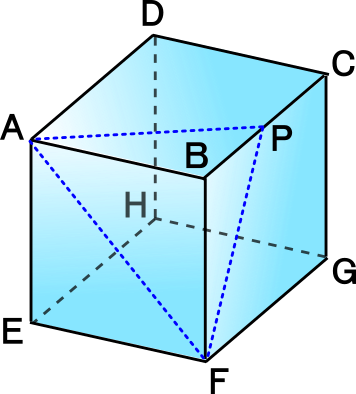
中学3年数学練習問題 三平方の定理 空間図形への応用 2

三平方の定理の応用問題 中学3年数学 Youtube
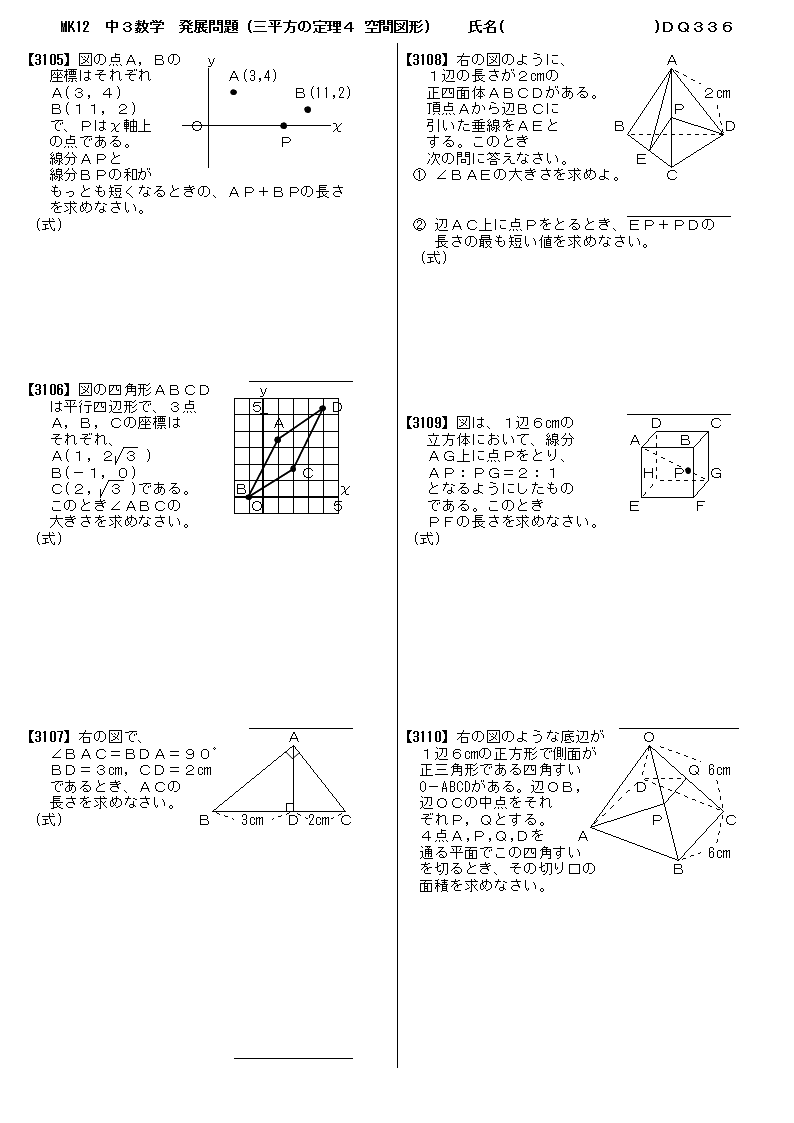
無料 中3数学 発展 応用問題 問題プリント 326 三平方の定理4 空間図形
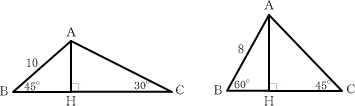
三平方の定理の応用 まとめ1 中学から数学だいすき

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
3
三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4
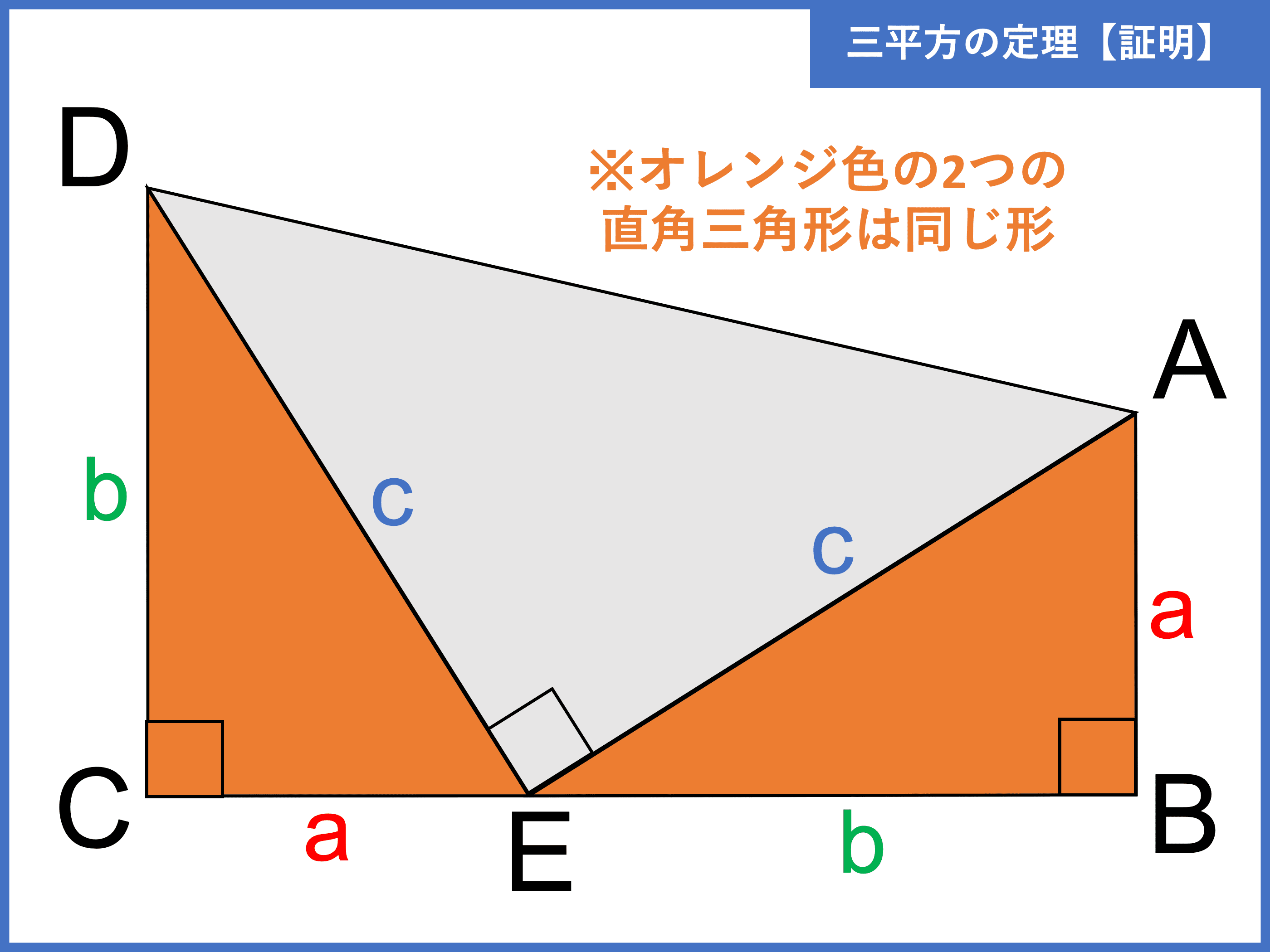
三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

Studydoctor三平方の定理の利用 中学3年数学 Studydoctor
中3数学 三平方の定理の応用 折り曲げ 2 Youtube

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

トレミーの定理とその3通りの証明 応用例 高校数学の美しい物語
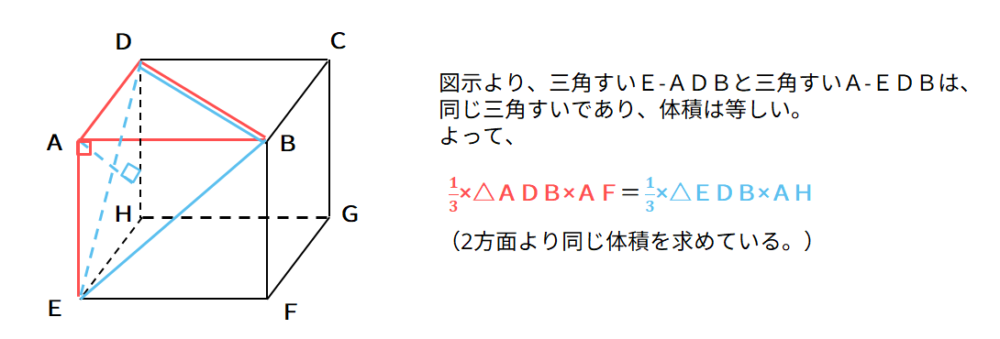
高校入試対策数学 空間図形と三平方の定理の対策問題 デルココ
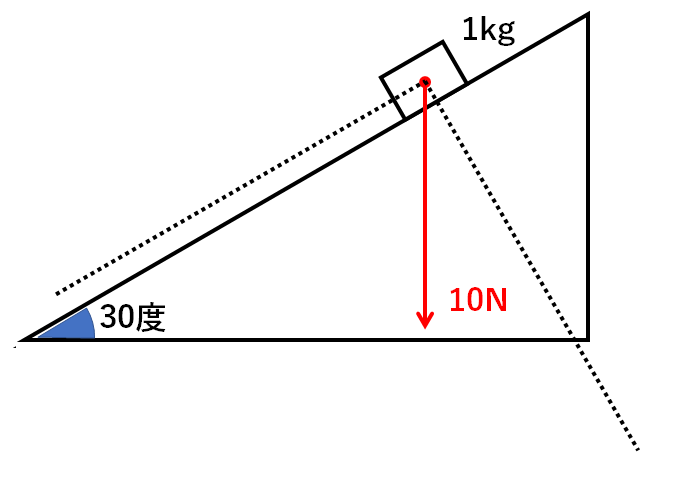
中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube

三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張

中学 数学 理科の復習サイト 三平方の定理 総合
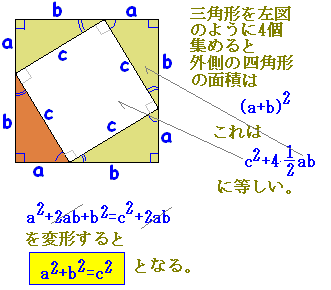
三平方の定理
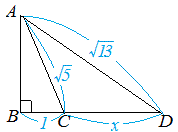
三平方の定理の応用
三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

等積変形を応用して典型題を解こう ヒポクラテスの月 も簡単にわかる 中学受験ナビ

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

応用問題の解説 三平方の定理と応用 1
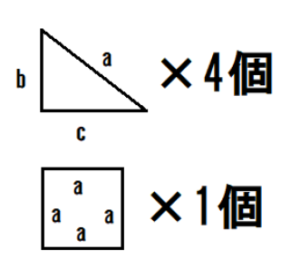
三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会
中学数学 三平方の定理の応用問題です 問題の考え方 解説 をお願い Yahoo 知恵袋
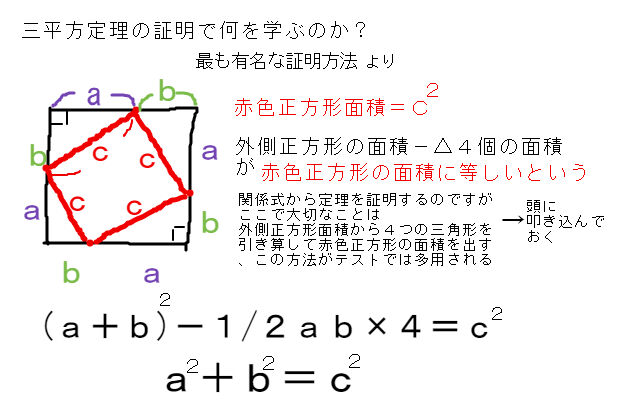
三平方定理の証明内容で最も覚えておくべきこと 中学 数学 理科の復習サイト
1

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 空間図形 三平方の定理 働きアリ
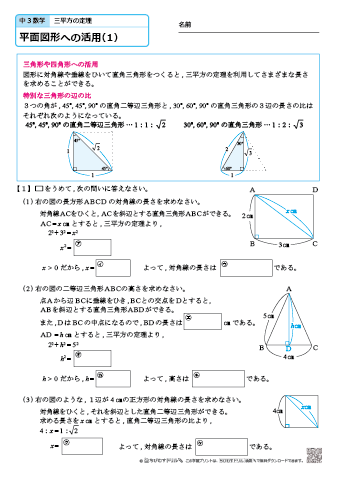
中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生
Sukinakazu Net
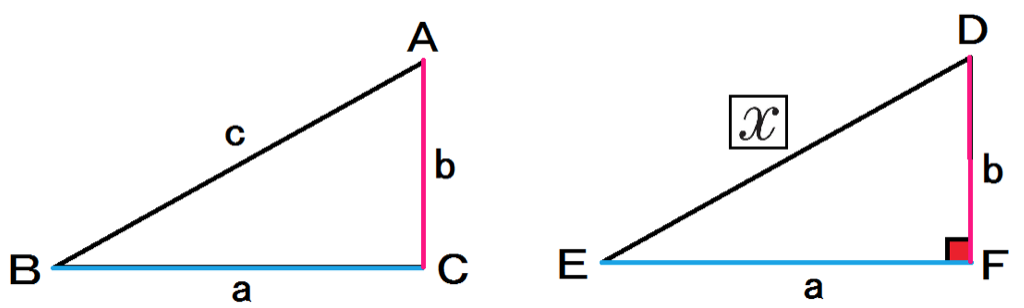
中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori
Tsumugi Ne Jp

数学 中3 61 三平方の定理 基本編 Youtube

無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1
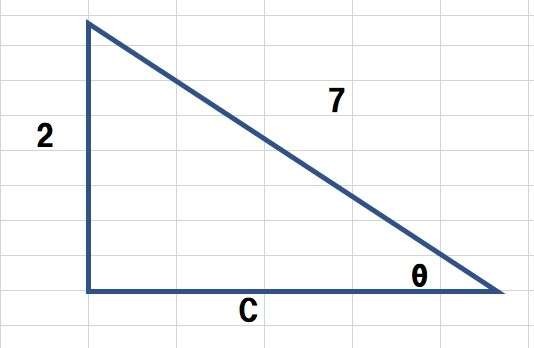
数学 三平方の定理を5秒で計算する裏ワザ 見ないと損する 予備校なら武田塾 京成佐倉校

知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より
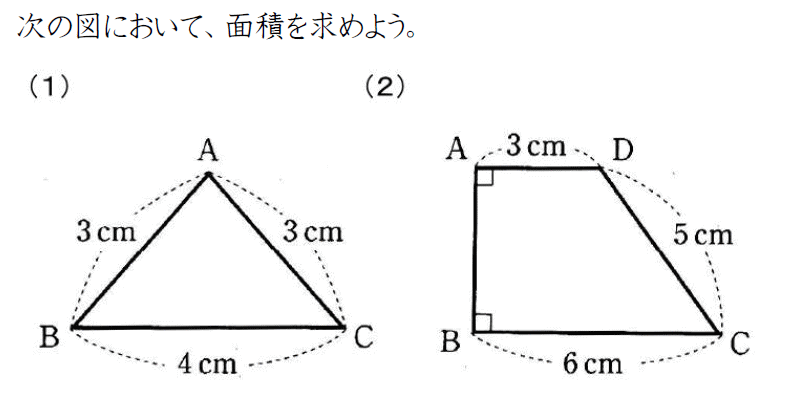
Studydoctor二等辺三角形や台形の面積と三平方の定理 中学3年数学 Studydoctor

ピタゴラスの定理 Wikipedia

三平方の定理 応用問題 関数

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
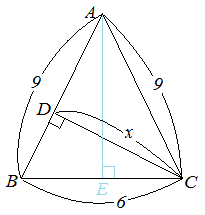
三平方の定理の応用
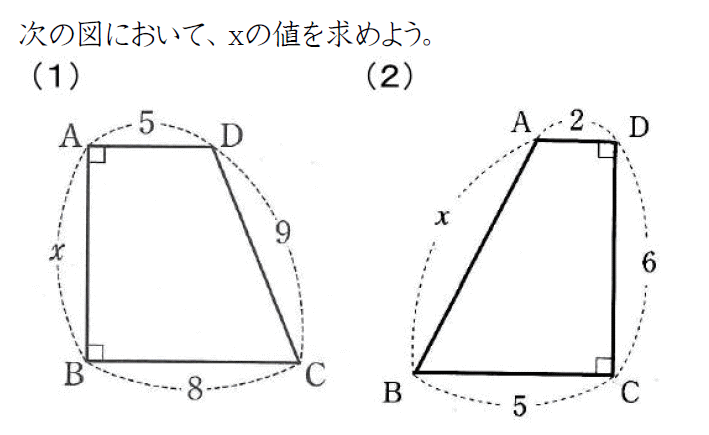
Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor

中3の数学の問題 セルモ大蔵 世田谷 の塾長ブログ
1
三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba
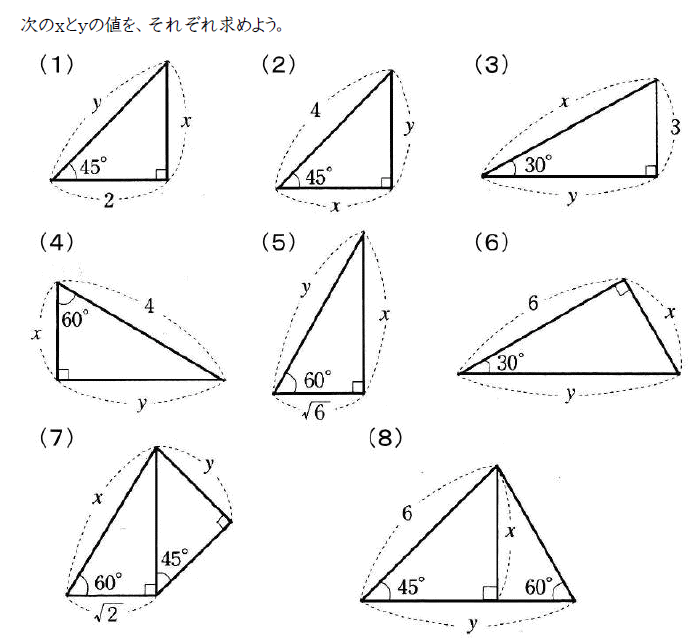
Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

中3数学 三平方の定理16 三平方の定理と面積 円 すべて無料 星組の中学数学講座
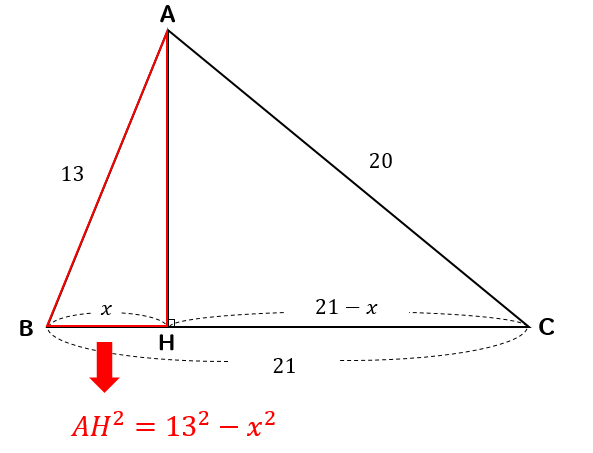
三平方の定理 方程式を利用する発展問題を解説 数スタ

中学数学 三平方の定理を利用する難問 応用 丁寧な解説 なぜか分かる はかせちゃんの怪しい研究室

ม 3 โน ตของ 中学数学 三平方の定理 基礎編 ช น Clearnote

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
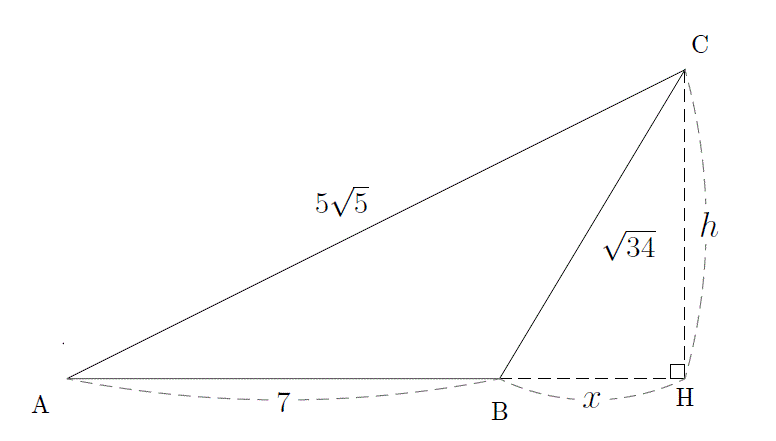
かみのドリル 三平方の定理

三平方の定理と相似の問題 無料で使える中学学習プリント

三平方の定理の応用 イ弋マ本ゼミナール

中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット
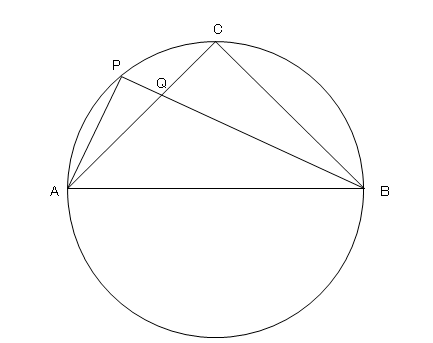
三平方の定理の応用 3 ネット塾

無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2

三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学
余弦定理

無料 中3数学 発展 応用問題 解答プリント 336 三平方の定理4 空間図形
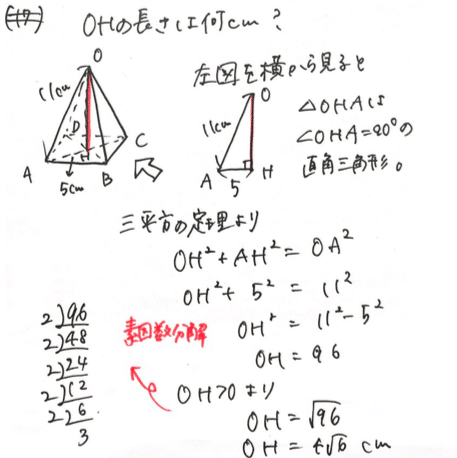
ピタゴラスは傲慢だった 数学検定3級から学ぶピタゴラスの定理 旧 ミヤラジ マチコ先生のラジ勉 公式note Note

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

中3数学 三平方の定理の応用 75度に要注意 Youtube
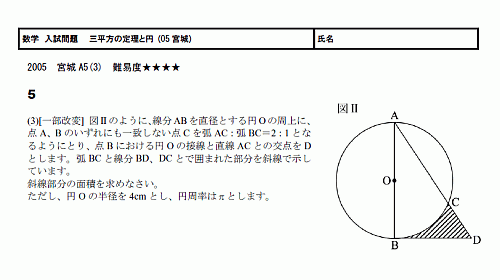
数学 高校入試 無料学習プリント教材
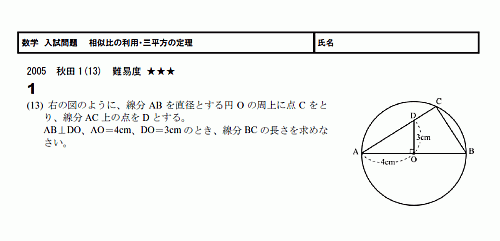
相似比の利用 三平方の定理 スタディーx
三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

中学数学 三平方の定理
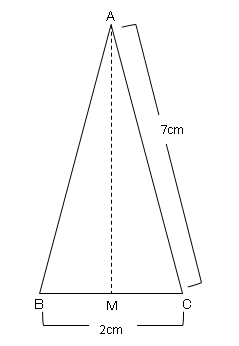
三平方の定理の応用 2 ネット塾
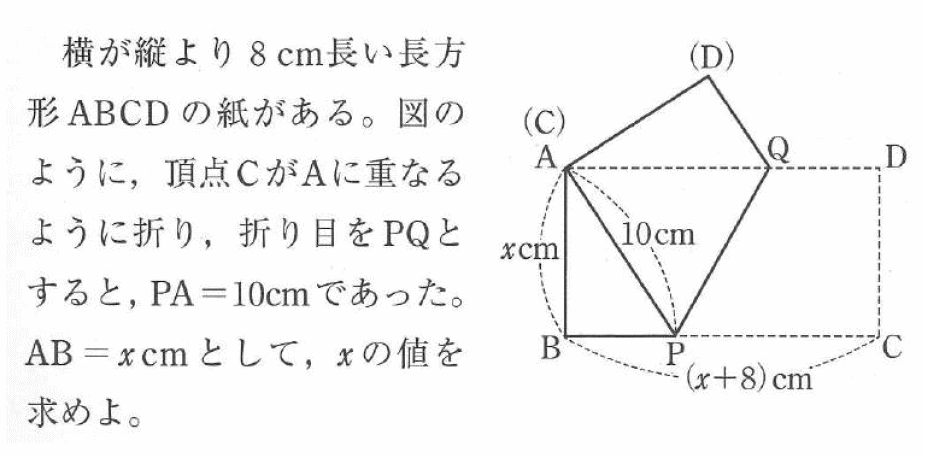
Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor

三平方の定理の応用問題が分かりません この問題を教えてください 数学 教えて Goo

世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
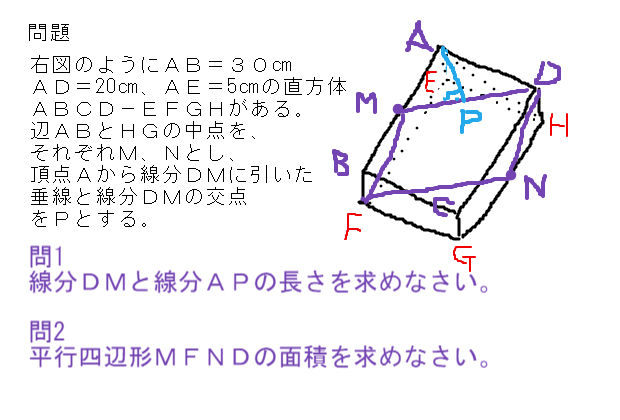
図形での三平方の定理の応用問題 正答率22 中学 数学 理科の復習サイト

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生

三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント

三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける Clearnote
三平方の定理 立体 苦手な数学を簡単に
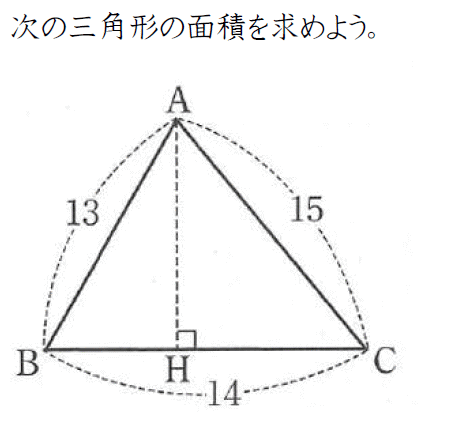
Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor
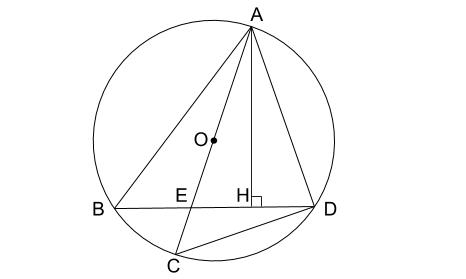
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

画像2 7枚 ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル
三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba
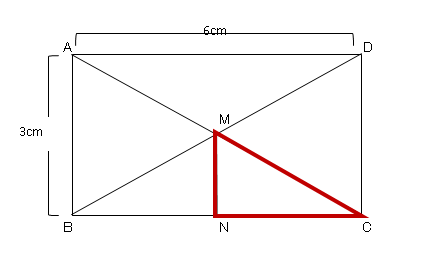
三平方の定理の応用 1 ネット塾

ピタゴラスの定理 Wikipedia
中学校数学 3年生 図形 三平方の定理 Wikibooks
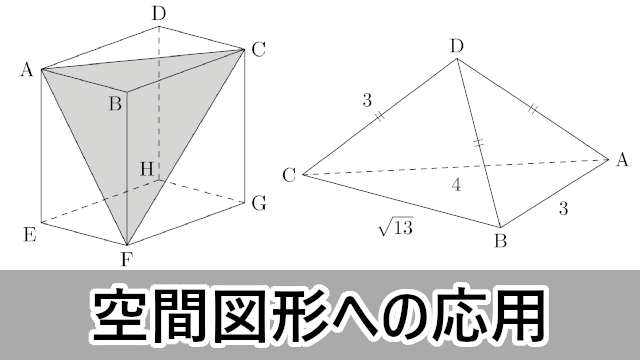
数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法

中線定理のいろいろな証明と問題 理系ラボ

ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル




