Unit Circle X2+y21
First change the disk (x − 1) 2 y 2 = 1 (x − 1) 2 y 2 = 1 to polar coordinates Expanding the square term, we have x 2 − 2 x 1 y 2 = 1 x 2 − 2 x 1 y 2 = 1 Then simplify to get x 2 y 2 = 2 x, x 2 y 2 = 2 x, which in polar coordinates becomes r 2 = 2 r cos θ r 2 = 2 r cos θ and then either r = 0 r = 0 or r = 2 cos θ r = 2 cos θ Similarly, the equation of the paraboloid changes to z.

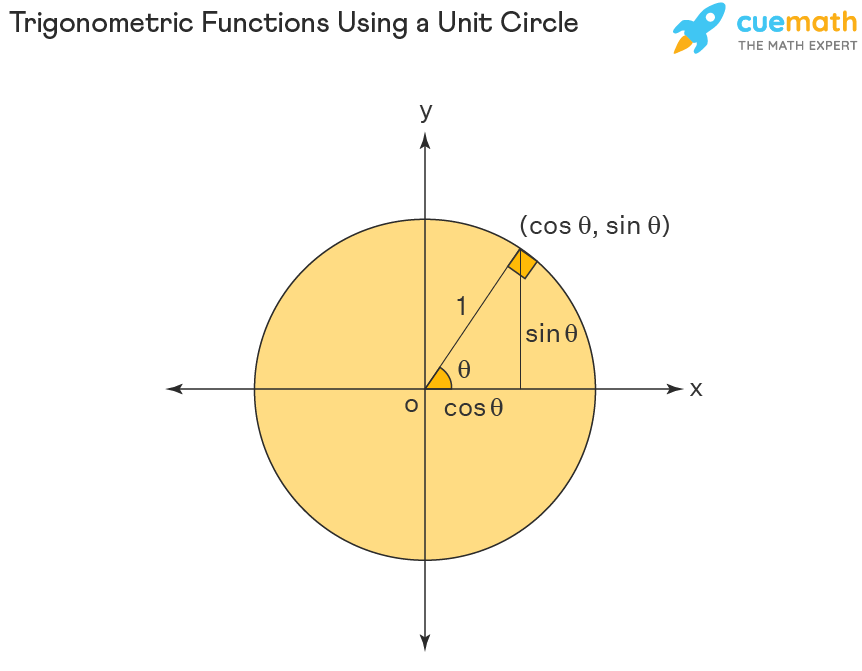
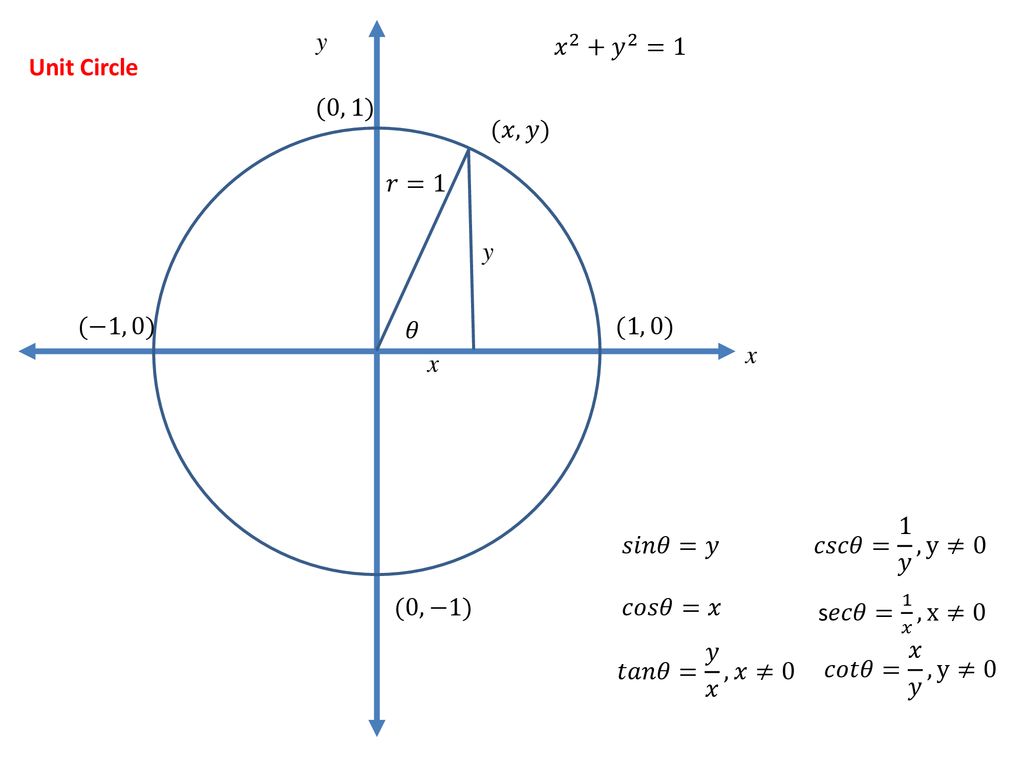
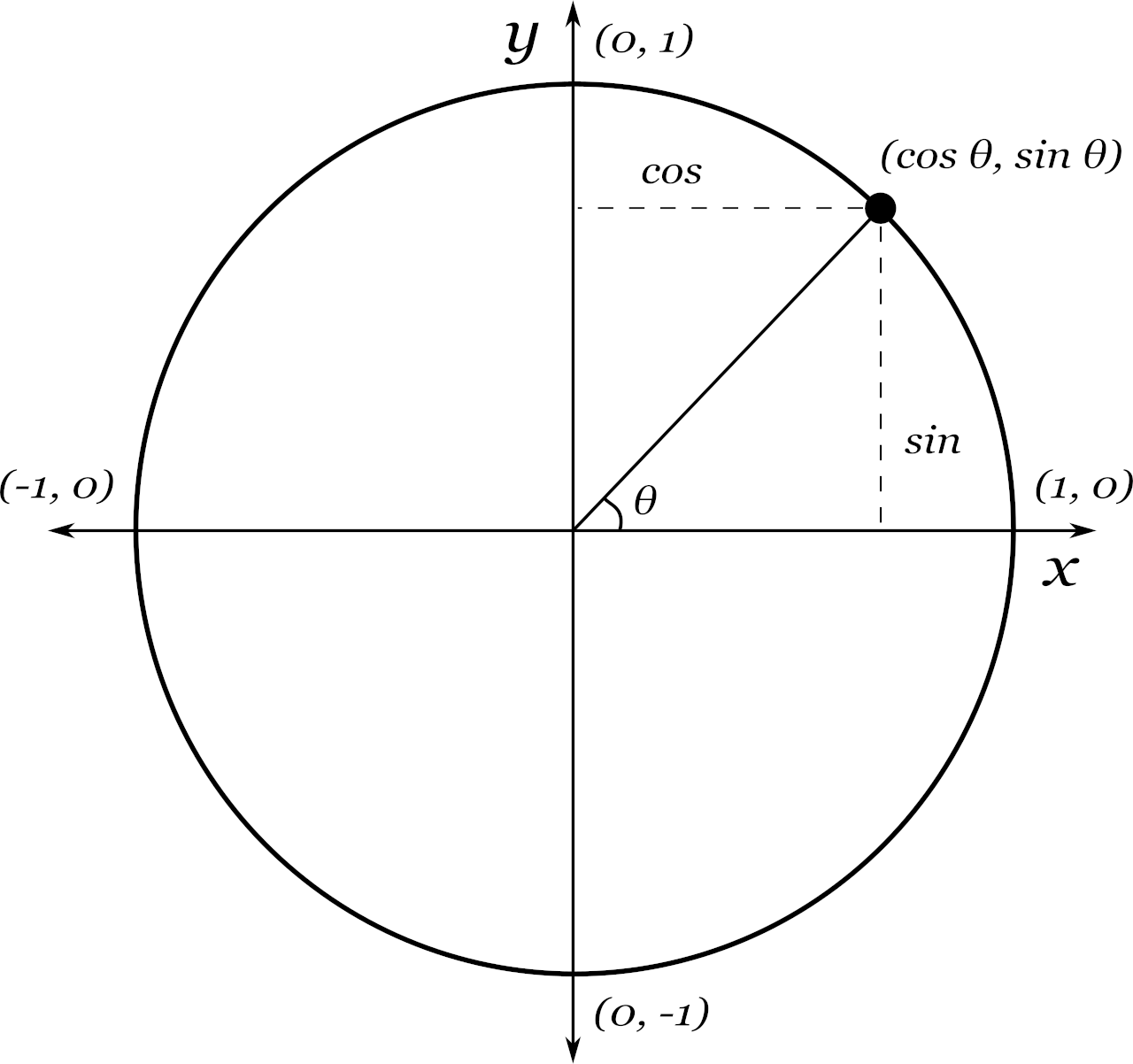
Unit circle x2+y21. A x B y C y/ x D x E y (1,0) 7T What is the csc 3 ?. This is simplified to obtain the equation of a unit circle Equation of a Unit Circle x 2 y 2 = 1 Here for the unit circle, the center lies at (0,0) and the radius is 1 unit The above equation satisfies all the points lying on the circle across the four quadrants. Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides x 2 y 2 = 1 2 But 1 2 is just 1, so x2 y2 = 1 (the equation of the unit circle) Also, since x=cos and y=sin, we get (cos (θ))2 (sin (θ))2 =.
Radian measure is direct result of a central angle that has its vertex at the center of a unit circle, a circle having a radius of one Unit circle (equation x 2 y 2 = 1) If we consider point P on a unit circle in the first quadrant. True The sine and cosine functions are sinusoidal functions That means when the graph of y = cos x is shifted to the right π/2 units to obtain the graph of y = cos(xπ/2), the graph is same as the graph of y = sin x. That is, at any time \(t\) the particle is at a point \((x, y)\) on the unit circle \(x^2 y^2 = 1\text{}\) We plot points at different times to see how the particle moves on the circle The particle completes one full trip counterclockwise around the circle every \(2\pi\) units of time.
(1)To come up with this, remember that we can parameterize a circle x2 y2 = 1 in R2 by = cos t, = sin (and, as increases, this goes around the circle counterclockwise) Here, we’re looking at x 2y = 9;. This is the equation of the unit circle and so the two parametric equations are a parameterization of the unit circle Now, consider x = sin ( t ), y = cos ( t );. 405 Trigonometric Functions of Any Angle This is an original lesson based on OpenStax Precalculus lesson 5253 Figure 1 London Eye credit (pixabay/skeeze) The London Eye is a farris wheel with a diameter of 394 feet By combining the ideas of the unit circle and right triangles, we can describe the location of any capsule on the Eye with.
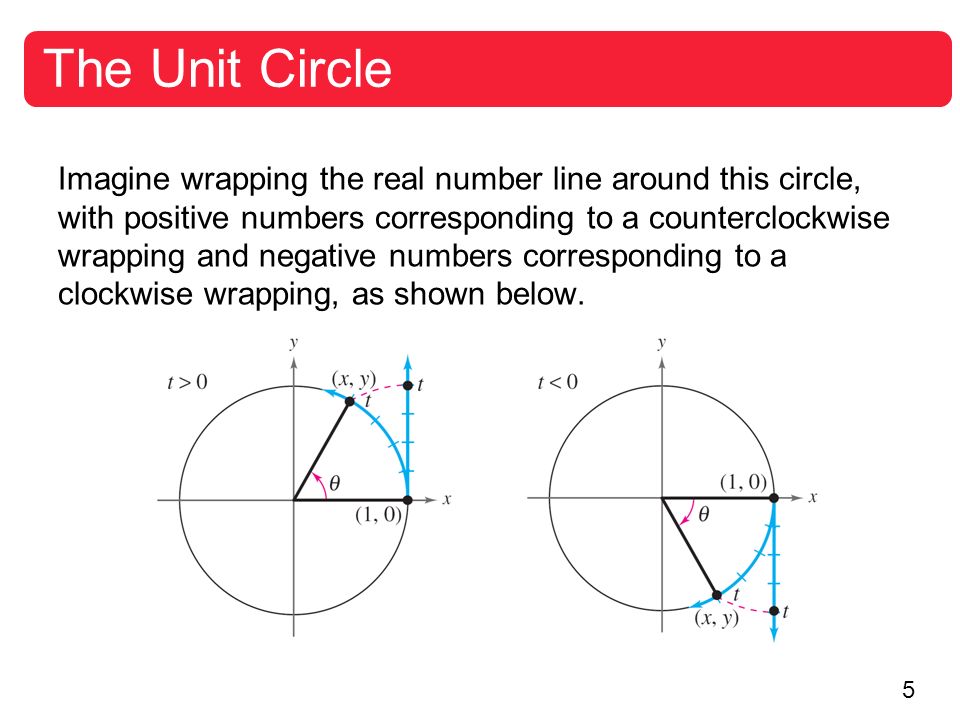
The unit circle is a circle of radius 1 unit that is centered on the origin of the coordinate plane The unit circle is fundamentally related to concepts in trigonometry The trigonometric functions can be defined in terms of the unit circle, and in doing so, the domain of these functions is extended to all real numbers The unit circle is also related to complex numbers. Let f ( x, y) = e x 2 y 2 on the disk D = { ( x, y) x 2 y 2 ≤ 1 } We will evaluate ∬ D f ( x, y) d A In rectangular coordinates the double integral ∬ D f ( x, y) d A can be written as the iterated integral ∬ D f ( x, y) d A = ∫ x = − 1 x = 1 ∫ y = − 1 − x 2 y = 1 − x 2 e x 2 y 2 d y d x. SECTION 51 The Unit Circle 403 point P1x, y2 on the unit circleThe point P1x, y2 obtained in this way is called the terminal point determined by the real number t y 0 1 x t0 (a) Terminal point P 1x, y2 determined by t 0 (b) Terminal point P1x, y2 determined FIGURe 2 by t 0 The circumference of the unit circle is C 2p112 2p.
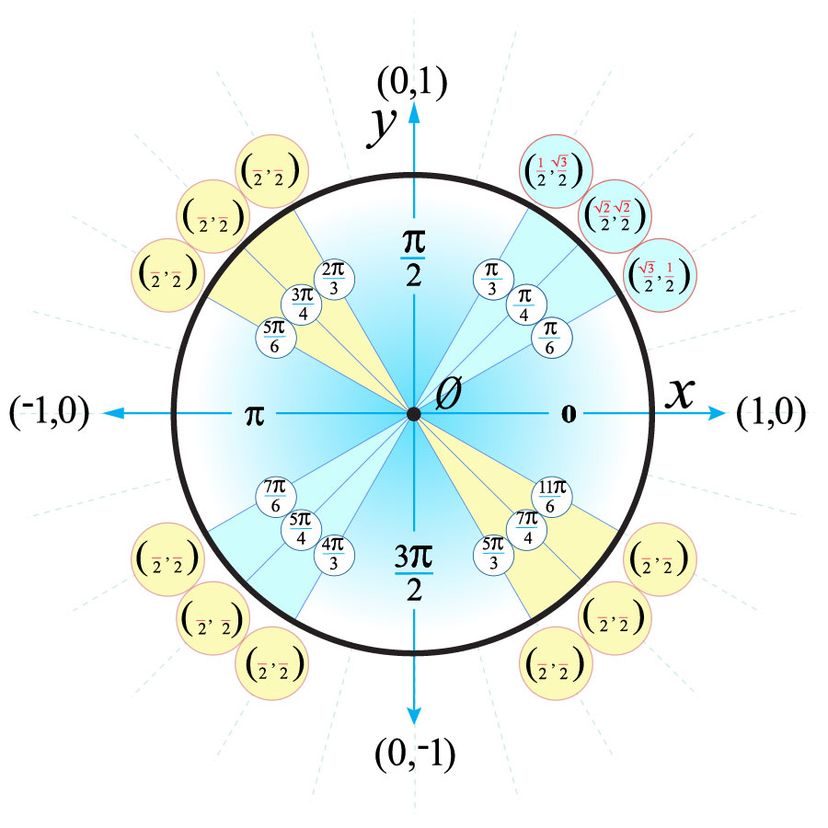
Unit Circle Trigonometry Coordinates of Quadrantal Angles and First Quadrant Special Angles x y 1 1 1 1 0o 90o 180o 270o 360o 30o 1o 60o 150o 210o 240o 300o 330o 135o 45o 225o 315o Putting it all together, we obtain the following unit circle with all special angles labeled. X^2 y^2 = 1 ——→ 2x 2y y’ = 0 , so y’ = x/y at the point (x, y) = which is m ( the slope) at that point So the equation of lines tangent y = ( x/y) x b but since (x,y) is a point on the unit circle x^2 y^2 = 1 the above will give { by multiplying both sides by y} y^2 = x^2 by imply by = y^2 x^2 = 1 —> b = 1/y. Then, Q x = 1 2 Q x = 1 2 and P y = − 1 2, P y = − 1 2, and therefore Q x − P y = 1 Q x − P y = 1 Notice that F was chosen to have the property that Q x − P y = 1 Q x − P y = 1 Since this is the case, Green’s theorem transforms the line integral of F over C into the double integral of 1 over D By Green’s theorem,.
Find stepbystep Probability solutions and your answer to the following textbook question The unit circle $\{ (x, y) x^2y^2 = 1\}$ is divided into three arcs by choosing three random points A,B,C on the circle (independently and uniformly), forming arcs between A and B, between A and C, and between B and C. Graph of the function and that is different is a graph of the culinary different access we're plus ones were pretty equal to one, and obviously if one is in is defined in this area and they have to and after and the force of unity calculate each off the their formula and the Romanoff it funds also So we're starting First of all, we can diet access choir plus y squared equal to one, or it is. We now expand the above equation and group like terms 2 x 2.
Y)on C through the relation r = h x;. 8T Find the solution set of 4 sin2 (x) = 1, where 0 x 2 9T A 10foot ladder is leaning against a vertical wall Let h be the height of the top. The equation of a circle of radius r centered at the origin (711) x 2 y 2 = r 2 Note the x coordinate and the y coordinate can take on negative values, depending on the quadrant of the terminal side of the angle Example 712 Find the y coordinate of point A ( − 5 9, y) if point A lies in QIII on the unit circle.
y = 3/4x25/4 We could use calculus but first as with all Mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case x^2 y^2 = 25 represents a circle of centre (a,b)=(0,0) and radius r=5 First verify that (3,4) actually lies on the circle;. 勾股 勾股定理说明:在直角三角形里,斜边的平方等于另外两边的平方的和: x 2 y 2 = 1 2 但 1 2 是 1,所以: x 2 y 2 = 1 (单位圆的方程) 因为 x=cos 和 y=sin,我们得到: (cos(θ)) 2 (sin(θ)) 2 = 1 一个有用的 "恒等式" 重要的角:30°、45° 和 60° 你应该尝试牢记这些角度的正弦、余弦和正切的. The unit circle chart shows the position of the points along the unit circle that are formed by dividing the circle into eight and twelve parts The coordinates of each point can be solved for using the one of the two corresponding special triangles Figure 1 Unit Circle Chart π (pi).
If we rewrite this as x 3 2 y 3 2 = 1, then we can write x 3 = cost, y 3 = sint 1. And the fact I'm calling it a unit circle means it has a radius of 1 So this length from the center and I centered it at the origin this length, from the center to any point on the circle, is of length 1 So what would this coordinate be right over there, right where it intersects along the xaxis?. 3 EX 1 Let r(t) be the parameterization of the unit circle centered at the origin Draw these vector fields and think about how the fluid moves around that circle F⇀(x,y) = 2i^ When F(x,y) is parallel to the tangent line at a point, then the maximum flow is along a circle When F(x,y) is perpendicular to the tangent line at a point, then there is no.
1) g(z 0) 2 If Dis a plane region with oriented boundary @D= C, then Z C Pdx Qdy= ZZ D @Q @x @P @y dxdy 3 If Dis a simply connected plane region, then F = (P;Q) is a gradient vector eld rgif and only if F satis es the mixed partials condition @Q @x = @P @y (Recall that a region Dis simply connected if every simple closed curve in. In a unit circle x 2 y 2 = 1, why can you substitute the x and y with cos and sin?. X = rcost y = rsint This can easily be verified, as x^2 y^2 =.
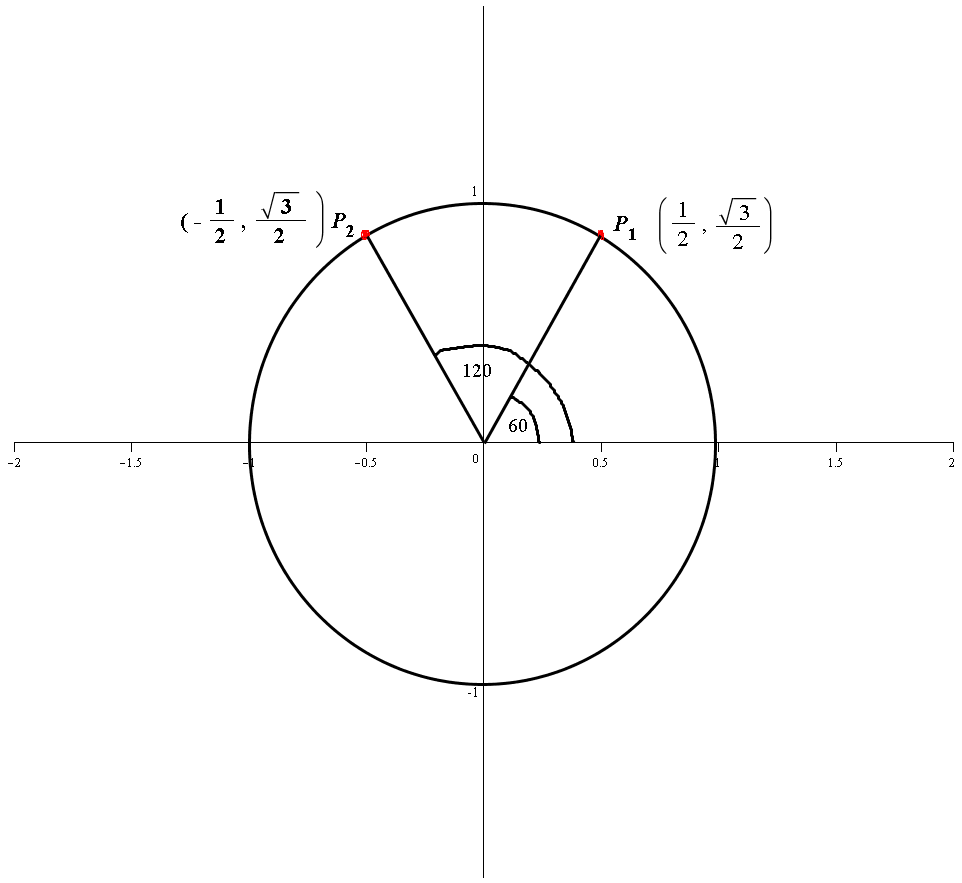
( θ)) However, to my understanding, cos is the adjacent side over the hypotenuse ( x r) and sin is the opposite side over the hypotenuse ( y r ). y1=x1=0707 and y2=x2=0707 Concluding that the line y = x intercept the unit circle x^2y^2=1 at points (0707, 0707) and (0707, 0707) douwdek0 and 1 more users found this answer helpful heart outlined Thanks 1 star outlined star outlined star outlined. X^2y^2=1 radius\x^26x8yy^2=0 center\ (x2)^2 (y3)^2=16 area\x^2 (y3)^2=16 circumference\ (x4)^2 (y2)^2=25 circlefunctioncalculator x^2y^2=1 en.
Y x 2 y =4 (1) ie, a circle of radius 2 cen tered at the origin W e start b y asso ciating p osition v ector r to eac h p oin t(x;. Dswhere Cis the upper half of the unit circle x 2 y = 1 First, we must write Cin parametric form The upper half of the unit circle is 268 CHAPTER 5 VECTOR CALCULUS the given points can be parametrized by x= 1, y= t, 1 t 2 Thus Z C 2 2xds = Z 2 1 2 p 1dt = 2 3 Therefore Z C 2xds= 5 p 5 1 6 2 Two other integrals can be obtained using. { (x = 2 3cost),(y = 1 3sint) } } \\ \\ \\pi le t le 5pi The Cartesian equation of a circle with centre (a,b) and radius r is (xa)^2 (ya)^2 = r^2 And so the equation (x2)^2 (y1)^2 = 9 represents a circle of centre (2,1) and radius 3 The parametric equations of a circle of centre (0,0) and radius r are;.
One moves along the curve C 1, the parabola defined by y = 2 x 21 The other particle moves along the curve C 2, the bottom half of the circle defined by x 2 (y1) 2 = 1, as shown in Figure 1532 Force is measured in pounds and distances are measured in feet Find the work performed by moving each particle along its path. Method 2 Use calcus Differentiate x^2 y^2 = 1 We get slope M1 = x/y To have perpendicularity M1*M2 = 1 M2= y/x Equation of normal Y = M2*X C C= 0, therefore normal passes through the orgin. circle x2 y2 = 4, the cross sections perpendicular to the xaxis are right isosceles triangles with a leg on the base of the solid 13 Picture for Example 4 14 Example 5) Find the volume of the solid whose base is bounded by y = x 1 and y = x21, the cross sections perpendicular to the xaxis are rectangles of height 5.
Answer to (1) Find the average value of the function \sqrt{x^{2}y^{2}} over the first quadrant of the unit circle using polar coordinates. X2 y2 = 1, x 2 y 2 = 1, 🔗 and this is the equation of the unit circle a point (x, y) ( x, y) lies on the unit circle if and only if x2 y2 = 1 x 2 y 2 = 1 Figure 221 Coordinates of a. Therefore the circle $$\{(x,y) \in \b R^2 x^2 y^2 = 1\} = f^{1}(\{1\})$$ is closed in $\b R^2$ Your set is also bounded, since, for example, it is contained within the ball of radius $2$ centered at the origin of $\b R^2$ (in the standard topology of $\b R^2$) Since $\{(x,y) \in \b R^2 x^2 y^2 = 1\}$ is a closed and bounded subset of $\b R^2$, the HeineBorel.
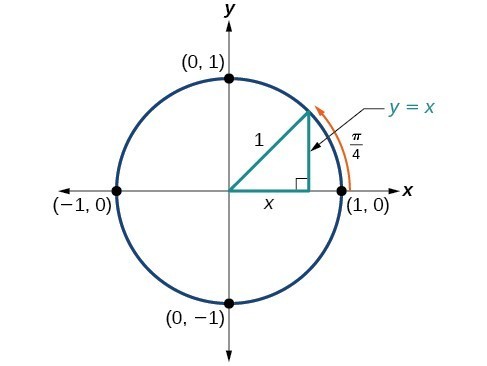
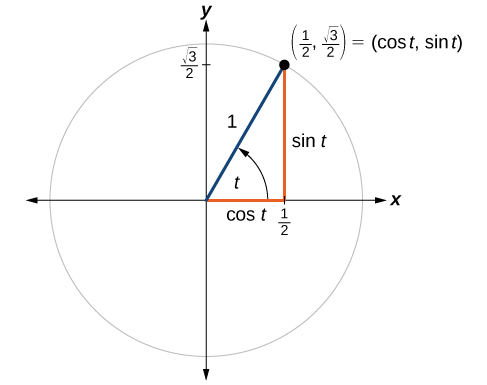
Example 1 Find the points of intersection of the circle with the line given by their equations (x 2) 2 (y 3) 2 = 4 2x 2y = 1 Solution to Example 1 We first solve the linear equation for y as follows y = x 1/2 We now substitute y in the equation of the circle by x 1/2 as follows (x 2) 2 ( x 1/2 3) 2 = 4 ;. So P is the point of intersection (in the first quadrant) of the circle x 2 y 2 = 1 and the line y = x Substituting x for y in the equation of the unit circle x 2 x 2 = 1 2x 2 = 1 x 2 = 1/2 k = ± 1/ √ 2 Because P is in the first quadrant, x = 1/ √ 2 and y = x, we have y = 1/ √ 2 also Thus the terminal point determined by π/4 is. T 0, 2 We apply the same procedure to eliminate the parameter, namely square x and y, and add the terms x2 y2 = sin 2 (.
Circle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples. Y i (2) The co ordinates x and y in (2)are not arbitrary {they are related through equation (1) This means that w e are free to assign a v alue only one of the co. The radius of the unit circle is 1 ∴ Required equation of circle \ \left ( x 4 \right)^2 \left ( y 2 \right)^2 = 1\, \ \Rightarrow\ \ x^2 y^2 8x 4y 19 = 0\ Concept Circle Standard Equation of a Circle Report Error.
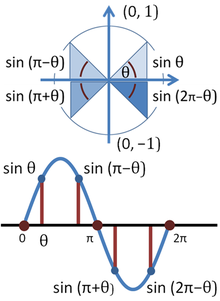
Example 1 Evaluate Z C (2 x2y) ds, where C is the upper half of the unit circle x2 y2 = 1 Solution the half circle can be parametrized by (x = cost, y = sint, 0 t p Then Z C (2 x2y) ds = Zp 0 (2 cos2 tsint) q (cost)02 (sint)02dt = Zp 0 (2 cos2 tsint) q sint2 cost2dt = Zp 0 (2 cos2 tsint)dt = 2t 1 3 cos3 t p 0 = (2p 1 3) (1 3) = 2p 2 3 3. θ of point P on the unit circle are P(x, y) (x, y), then sin (θ) = ?. List of trigonometric identities In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined Geometrically, these are identities involving certain functions of.
The unit circle x y2 = 1 is shown above, along with a triangle formed by using parts of the lines y = x, y = 1, and y=1 Looking at the picture, the area of the blue region is simply the area of the triangle, with a quarter of the area from the circle subtracted out. For this point, you can find a open ball of radius $\sqrt{1125^2 06^2}1$, which lies completely "outside" the blue unit circle and therefore lies completely in the complement of the unit circle In general, you can do this for any point not lying on the unit circle. The unit circle is defined by the equation x^2 y^2 =1 From elementary trigonometry we recall the identity (cos (t))^2 (sin (t))^2 =1 for all 0, 2p) This directly gives us our first parametrization of the unit circle Let x (t) = cos (t) and y (t) = sin (t).
Well, x would be 1, y would be 0.

If A X Y X 2 Y 2 25 And B X Y X 2 9y 2 144 Then A B Contains

Paramanand S Math Notes Theories Of Circular Functions Part 1
Solved The Circle X 2 Y 2 1 Cuts The X Axis At P And Q Another Circle With Centre At Q And Variable Radius Intersect The First Circle At R Above The Mathrm X Axis And Line Segment P Q
Unit Circle X2+y21 のギャラリー
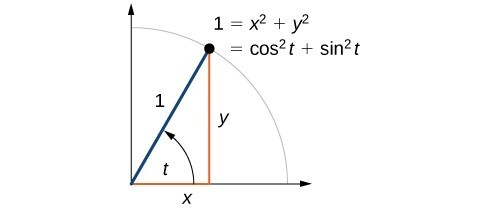
Unit Circle Sine And Cosine Functions Precalculus Ii

Solved The Unit Circle X 2 Y 2 1 Consists Of Four One To One Functions F 1 X F 2 X F 3 X And F 4 X See Figure A Find The Domain And A Formula For Each Function B Find The Inverse Of

Thomas Calculus 11e 8 1262 Pages 351 381 Flip Pdf Download Fliphtml5
Math 251 Diary Fall 08
How To Find A Missing Coordinate On A Unit Circle Dummies
View Question Unit Circle
Unit Circle Sine And Cosine Functions Precalculus Ii

Trigonometric Functions On The Unit Circle Given A Point On The

Unit Circle Video Trigonometry Khan Academy

The Set X Consists Of All Points Within And On The Unit Circle X 2 Y 2 1 Whereas The Set Y Consists Of All Points On And Inside The Rectangular Boundary X 0 X
Terminal Points On The Unit Circle
Cerritos Edu

Unit Circle And Radians Unit 3 Radians L

Trigonometric Functions And The Unitary Circle X Engineer Org
Unit Circle Equation Of A Unit Circle Unit Circle Chart

The Set X Consists Of All Points Within And On The Unit Circle X 2 Y 2 1 Whereas The Set Y Consists Of All Points On And Inside The Rectangular Boundary X 0 X

Circles

Unit Circle Trigonometry Learning Math Math Concepts

4 2 4 4 The Unit Circle Trig Functions The Unit Circle Is Defined By The Equation X 2 Y 2 1 It Has Its Center At The Origin And Radius 1 0 Ppt Download

With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle Study Com

Left 1 2sqrt 2 Right Is A Point On Circle X 2 Y 2 Q Which Of The Following Is Not The Point On The Circle At 32 Units Distance From 1 2 Sqrt 2 A Left 1 2sqrt 2 Right B
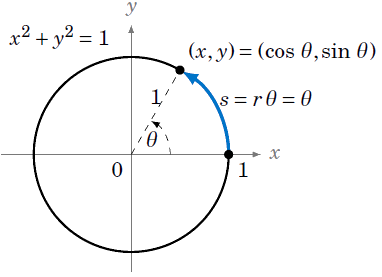
Graphing The Trigonometric Functions Opencurriculum
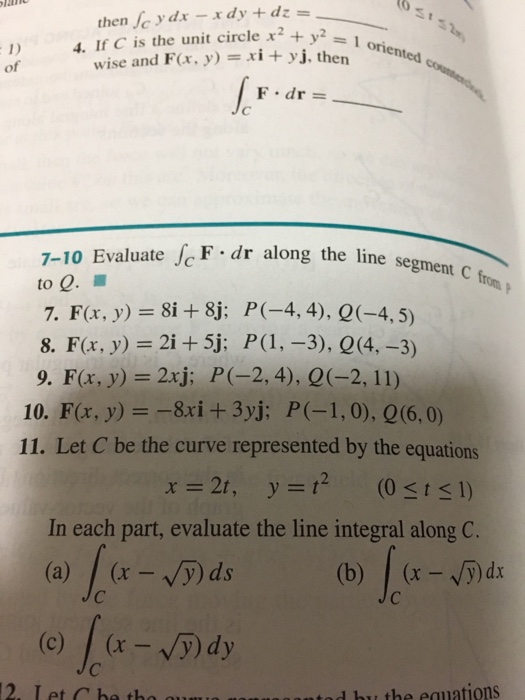
Solved If C Is The Unit Circle X 2 Y 2 1 Oriented Chegg Com
Unit Circle Wikipedia

Solved 4 A Evaluate Integral Sc F Dr For The Vector Chegg Com

The Unit Circle Ck 12 Foundation
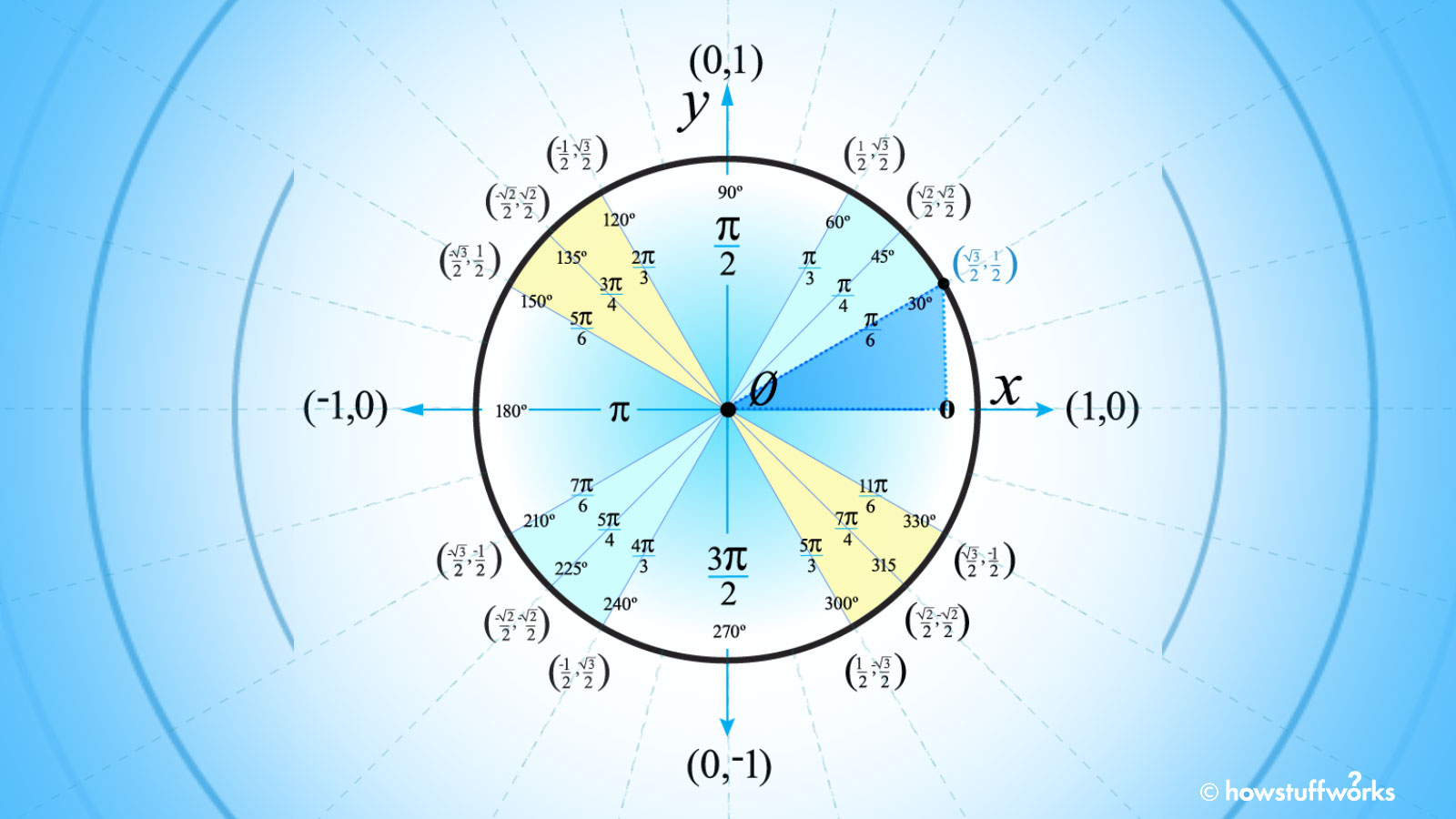
How To Use The Unit Circle In Trig Howstuffworks

Unit Circle Wikipedia

Complex Numbers Absolute Value
1
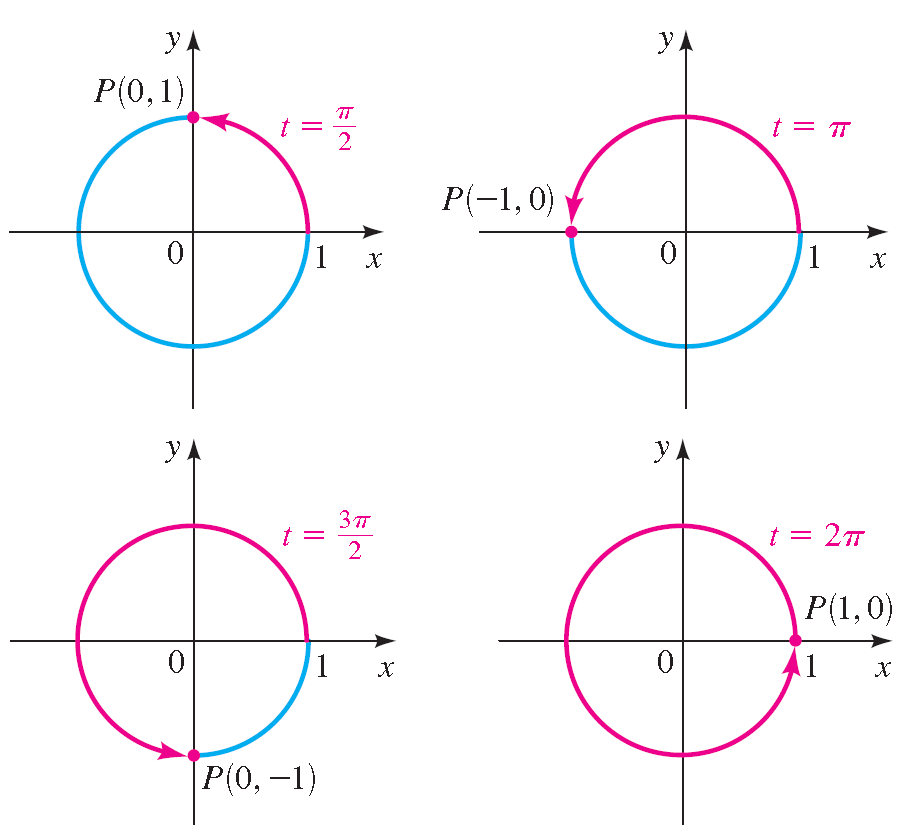
Terminal Points On The Unit Circle

Unit Circle

Unit Circle Trigonometry

Prove That The Unit Circle X 2 Y 2 1 Is A Closed Set Newbedev

Sine Function Sin X

Maths Form 2 Circles Aidagaskin
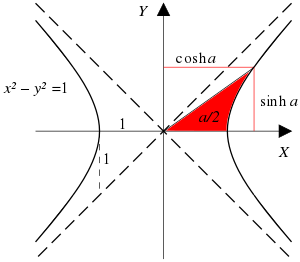
Inverse Hyperbolic Functions Wikipedia

Unit Circle
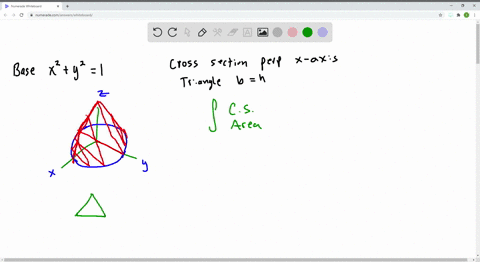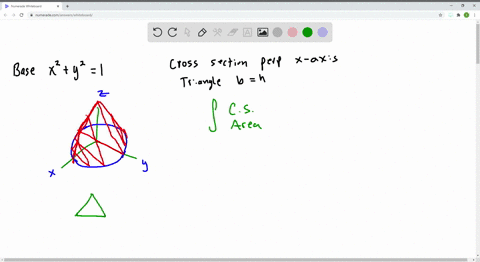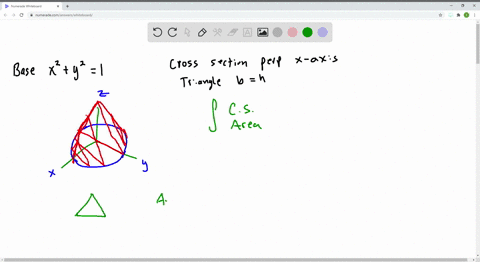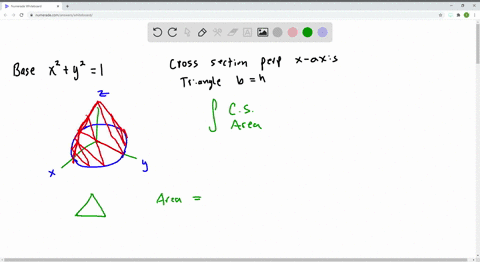
Solved Let B Be The Solid Whose Base Is The Unit Circle X 2 Y 2 1 And Whose Vertical Cross Sections Perpendicular To The X Axis Are Equilateral Triangles Show That The Vertical Cross Sections Have

Unit Circle
1 1 The Unit Circle Mathematics Libretexts
Solved Provide A Formula That Can Be Used To Determine Whether A Point Lies On A Circle That Is Cantered About 0 0 With A Diameter Of 12 Course Hero

Blank Unit Circle Worksheets Free To Print Now Matter Of Math

If The Radii Of The Circle X 1 2 Y 2 2 1 And X 7 2 Y 10 2 4 Are Increasing Uniformly W R T Times As 0 3 Unit S Is And 0 4 Unit S Then They Will Touch Each Other At T Equal To 45s
How Do You Graph X 2 Y 2 1 Socratic
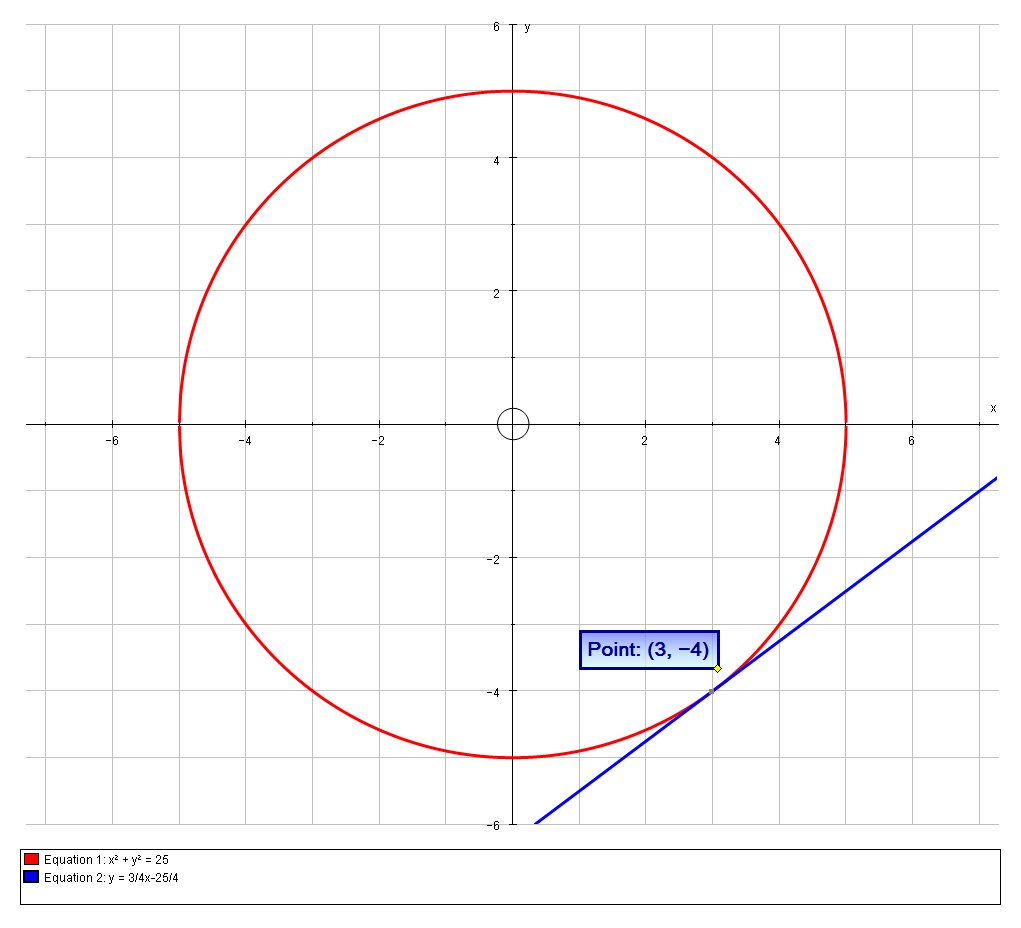
How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic
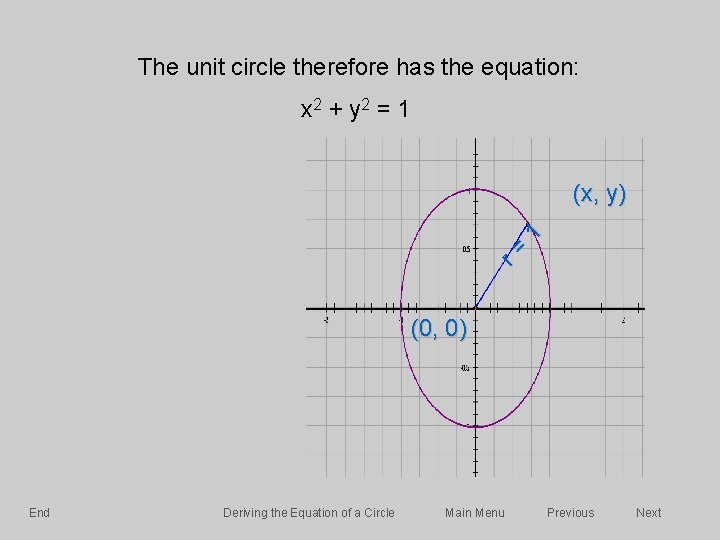
Skip Introduction A Closer Look At Graphing The

A With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle B Provide A
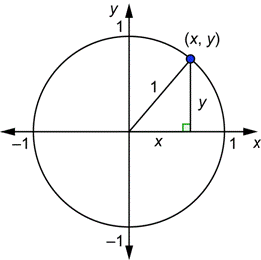
Unit Circle Trigonometry
1
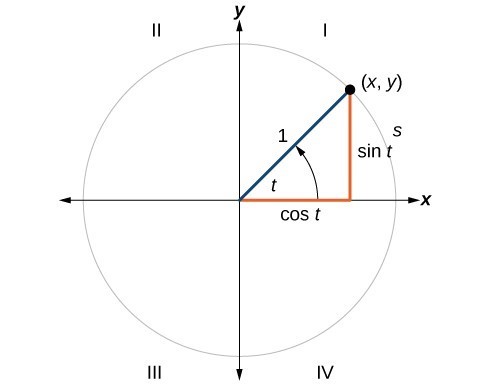
Unit Circle Sine And Cosine Functions Precalculus Ii
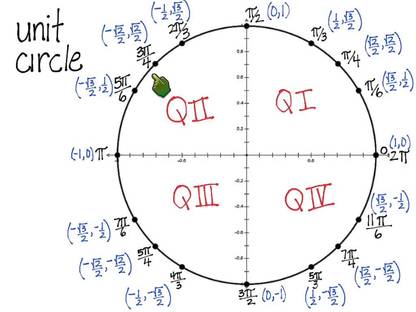
Measuring Your World
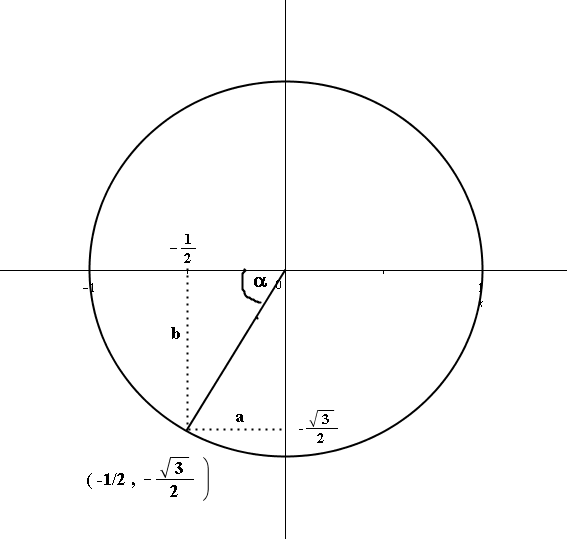
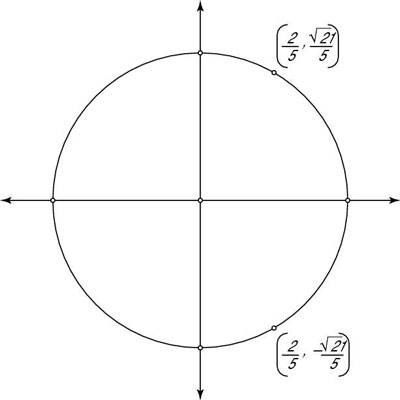
Find X Y On The Unit Circle Given That The X Coordinate Of P Is 1 2 And P Is In Quadrant Iii Socratic
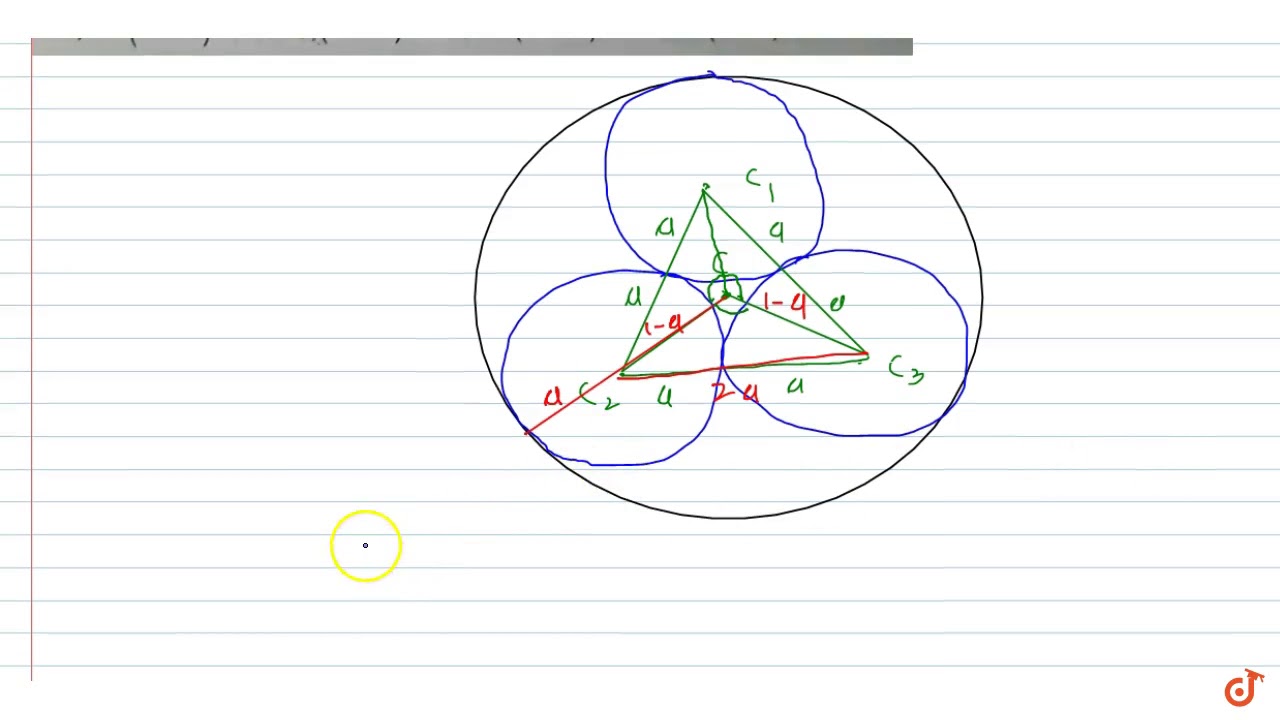
Inside The Unit Circle S X 2 Y 2 1 There Are Three Smaller Circles Of Equal Radius A Touches Youtube
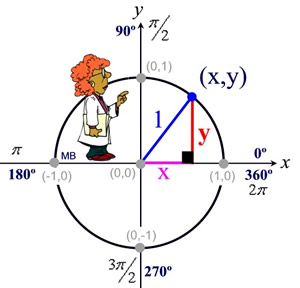
Unit Circle Mathbitsnotebook Ccss Math
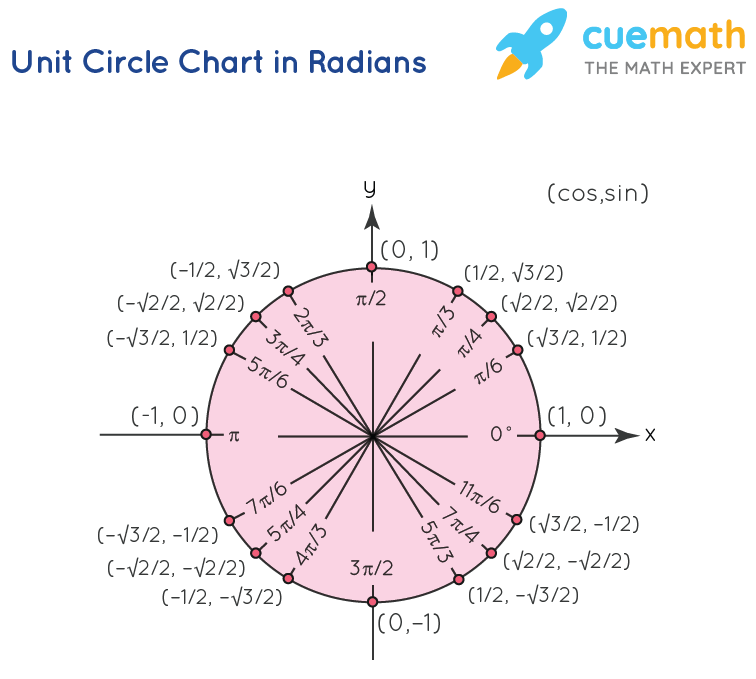
Unit Circle Equation Of A Unit Circle Unit Circle Chart
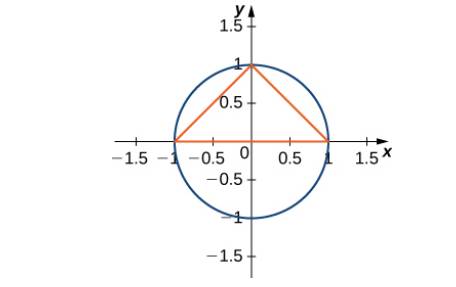
The Largest Triangle With A Base On The X Axis That Fits Inside The Upper Half Of The Unit Circle Y 2 X 2 1 Is Given By Y

Variant Of Pythagorean Triples Mathematics Stack Exchange

Example 2 Find Area Enclosed By Ellipse X2 Y2 B2 1

Misc 18 Mcq Area Of Circle X2 Y2 16 Exterior To Parabola
Is Math X 2 Y 2 1 Math An Even Or Odd Function Quora
How To Use The Unit Circle In Trig Howstuffworks

Trig Unit Circle Review Article Khan Academy
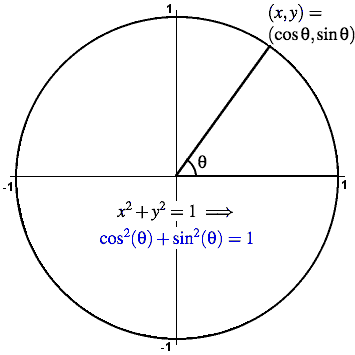
Trigonometry Facts The Amazing Unit Circle

Trigonometric Function The Unit Circle Ppt Download
Equation Of A Circle
Unit Circle Chart

6 A Plot Of The Unit Circle Satisfying X 2 Y 2 1 Download Scientific Diagram
A Is Uniformly Distributed In The Unit Circle With The Class Y Being Download Scientific Diagram
Unit Circle
If The Point X Sqrt 3 2 Is On The Unit Circle What Is X Socratic

Deformation Of The Unit Circle S X 2 Y 2 1 Under The Superflow Download Scientific Diagram

3 4 Circular Functions X 2 Y 2 1 Is A Circle Centered At The Origin With Radius 1 Call It The Unit Circle 1 0 Ex 1 For The Radian Measure Ppt Download

11 03 Graphs Of Circles Lesson Mathspace
Trigonometric Functions The Unit Circle Identify A Unit Circle And Describe Its Relationship To Real Numbers Evaluate Trigonometric Functions Ppt Download
Unit Circle Wikipedia
4 2 Trigonometric Functions The Unit Circle Ppt Download
Unit Circle Algebra And Trigonometry
Unit Circle Calculator Inch Calculator

Example 10 Find Area Enclosed Between Two Circles X2 Y2 4

Inside The Unit Circle S X Y X 2
3

Apc The Unit Circle
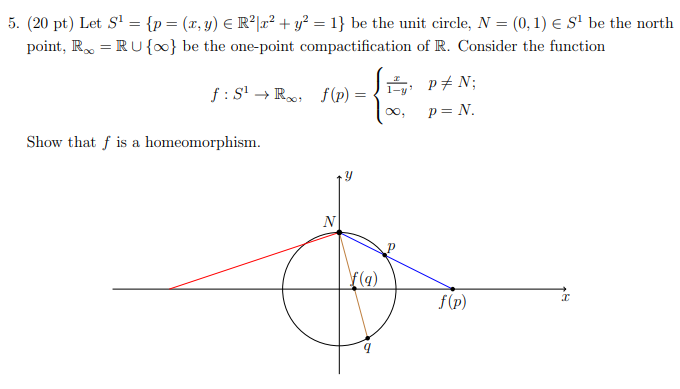
Solved Let S 1 P X Y R 2 X 2 Y 2 1 Be The Chegg Com

Answered At What Points Will The Line Y X Bartleby
Unit Circle
Let Rs Be The Diameter Of The Circle X2 Y2 1 Where Class 12 Maths Cbse
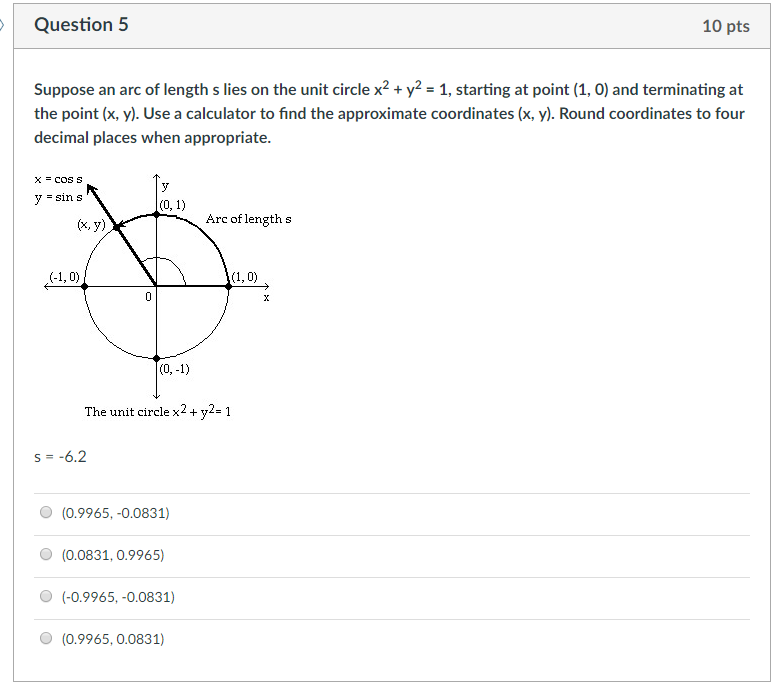
Solved Question 5 10 Pts Suppose An Arc Of Length S Lies On Chegg Com
Solved The Unit Circle Is Given For The X And Y Axis In The Chegg Com
Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download
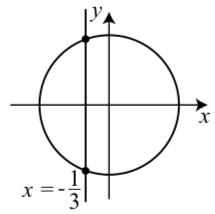
1 1 The Unit Circle Mathematics Libretexts
If We Let Math Y Sin X Csc X 2 Cos X Sec X 2 Math Then What Is The Minimum Value Of Math Y Math Quora

Example 7 Find Area Lying Above X Axis Included B W Circle

Deformation Of The Unit Circle S X 2 Y 2 1 Under The Superflow Download Scientific Diagram
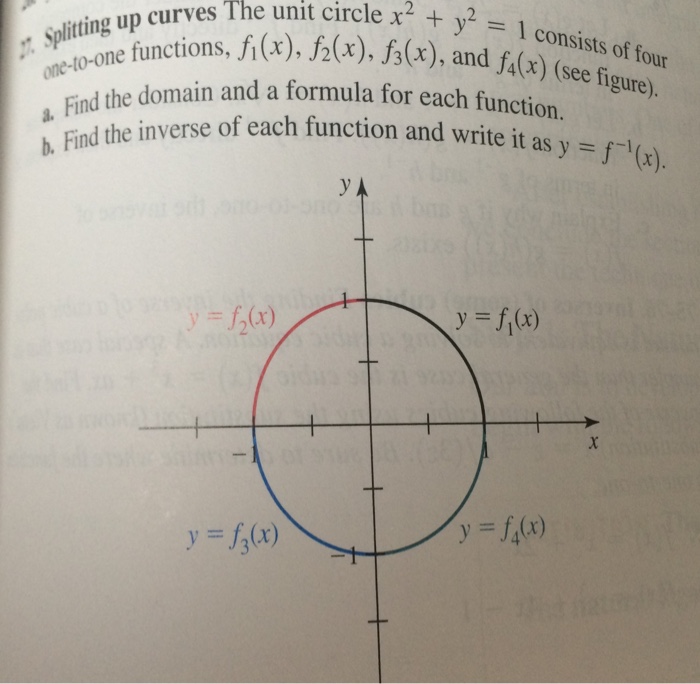
Solved Splitting Up Curves The Unit Circle X 2 Y 2 1 Chegg Com

Class 12 Example 7 63 Find The Points On The Unit Circle X 2 Y 2 1 Nearest And Farthest From 1 1 Youtube
Unit Circle Chart
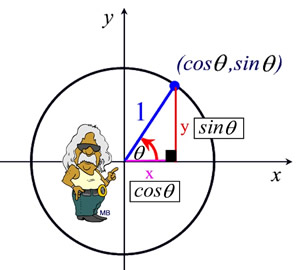
Unit Circle Mathbitsnotebook Ccss Math

Do Now Graph The Equation X 2 Y 2 1 Draw And Label The Special Right Triangles What Happens When The Hypotenuse Of Each Triangle Equals 1 Ppt Download
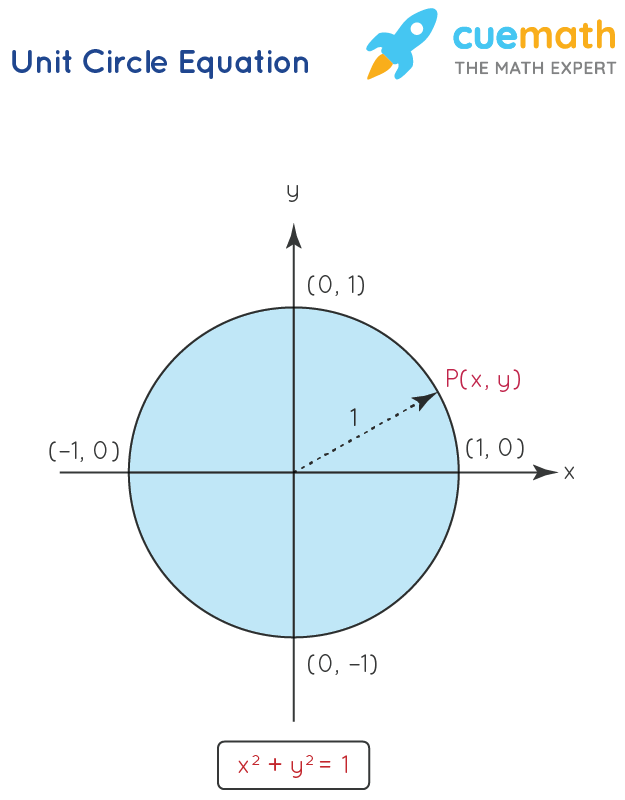
Unit Circle Equation Of A Unit Circle Unit Circle Chart

Deformation Of The Unit Circle S X 2 Y 2 1 In The Plane Z 1 Download Scientific Diagram




