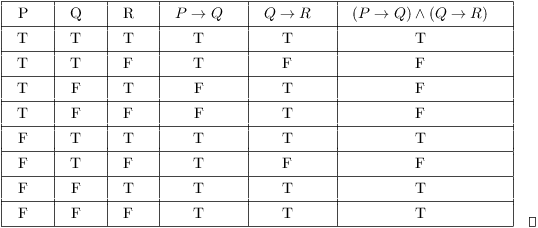
If P Then Q If Q Then R Therefore If P Then R
Using the definitions of the connectives in Section 02, we see that for this to be true, either P → Q P → Q must be true or Q→ R Q → R must be true (or both) Those are true if either P P is false or Q Q is true (in the first case) and Q Q is false or R R is true.

If p then q if q then r therefore if p then r. P → q (p implies q) (if p then q) is the proposition that is false when p is true and q is false and true otherwise Equivalent to finot p or qfl Ex If I am elected then I will lower the taxes If you get 100% on the final then you will get an A p I am elected q I will lower the taxes Think of it as a contract, obligation or pledge. Learning Objectives1) Interpret sentences as being conditional statements2) Write the truth table for a conditional in its implication form3) Use truth tabl. (p → q) ∧ (p → r) ├ p → (q ∧ r) If p then q;.
If P, then Q 2 If Q, then R 3 Therefore, if P, then R Disjunctive Syllogism (DS) 1 P or Q 1 P or Q 2 notP 2 notQ 3 Therefore, Q 3. Answer (1 of 3) Given P Q = R with P = R and R is perpendicular to P Consider a closed right angled triangle ABC with AC perpendicular to AB so that angle A is 90 degrees Let P & Q be represented, respectively by the vectors AB and BC, where as vector AC represents R (make a rough sketch of. P→Q means If P then Q ~R means NotR P ∧ Q means P and Q P ∨ Q means P or Q An argument is valid if the following conditional holds If all the premises are true, the conclusion must be true Some valid argument forms (1) 1 P 2 P→Q C Therefore, Q (2) 1 ~Q 2 P→Q C Therefore, ~P (3) 1 P 2 Q 3 (P ∧ Q)→R C Therefore, R (4) 1 P 2 P→Q 3 Q→R 4 R→S C Therefore, S.
Does the conclusion must be true?. ~p q↔p ~r→q Therefore, ~r Note that the statements "y is not an even number" and "y is an odd number" mean the same thing, and are therefore equivalent This argument has three premises ~p;. If an independent premise is removed, the support that other premises supply to the conclusion is not affected.
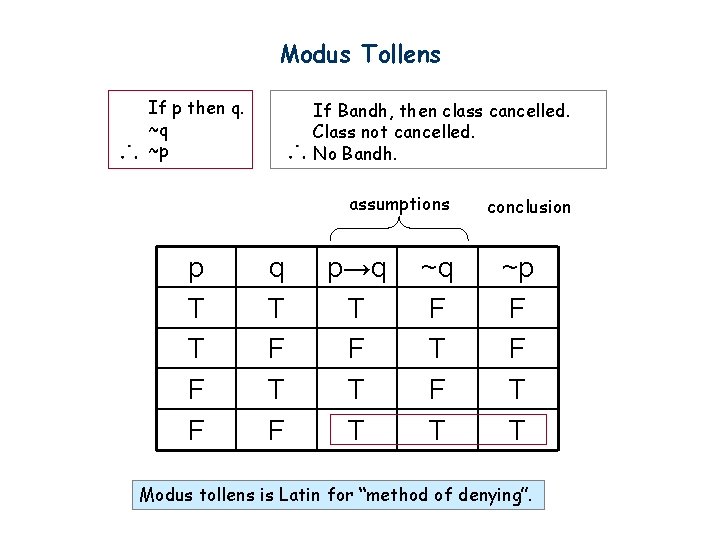
Two premises are both true But if Q →R and ~R are both true, then ~Q is also true For ~Q follows from Q →R and ~R, in virtue of modus tollens So, if the premises are all true, then so is ~Q That means that all the following formulas are true – P →Q, Q. If p then q p Therefore, q If p then q Notq Therefore, notp Exposition The consequent of a conditional statement is the part that usually follows "then" The part that usually follows "if" is called the "antecedent" I write "usually" here because there are many different ways to make a conditional statement, but we needn't go into. More generally, disjunctive elimination goes if p then q if r then q p or r therefore q Disjunctive elimination doesn’t make special mention of contradictory statements, as your argument above does, but one is entitled to draw the conclusion C from premises 1, 2, and 3 by virtue of this rul.
R means (p ^ q ) !. P → q q → r p∨q → r is a perfectly valid argument Let p =“I sleep a lot”, q =“I don’t do any homework” and r =“I will do well in this class” Then this translates to “If I sleep a lot, then I don’t do any homework If I don’t do any homework, then I. QUESTION 1 Modus tollens has this argument pattern The correct option for this question is If p, then q Not q Therefore, not p It is because in Modus Tollens p and q are prepositions Modus Tollens states that if p implies q, and q is false, View the full answer.
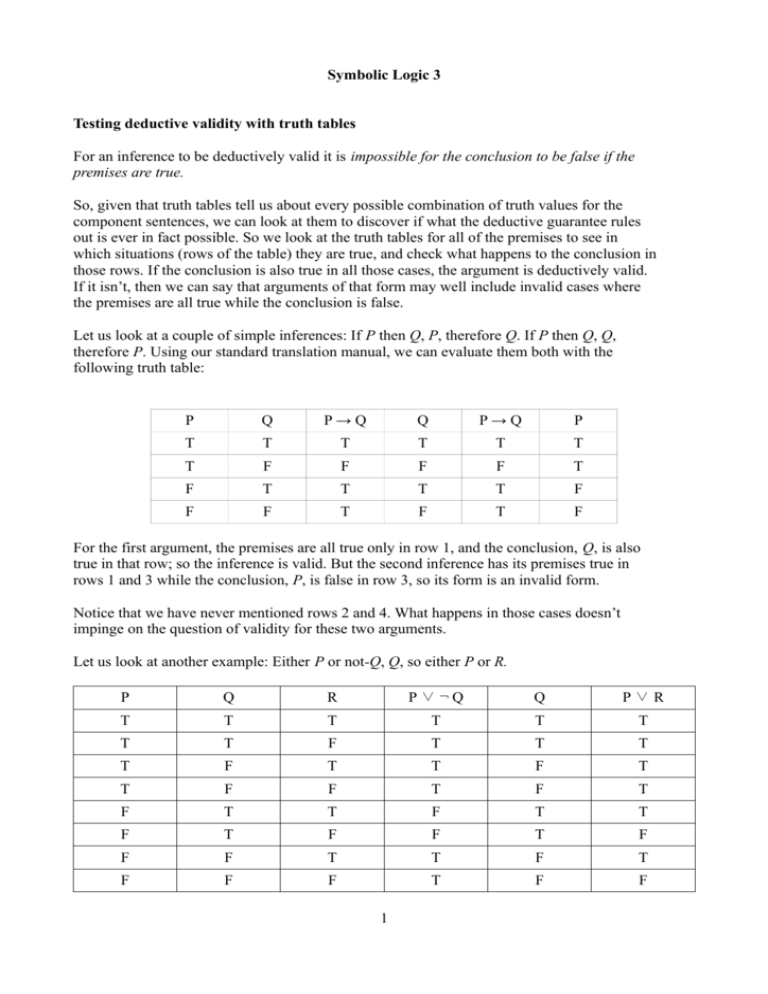
If P then Q, Q, therefore P Using our standard translation manual, we can evaluate them both with the following truth table P Q P → Q Q P → Q P T T T T T T T F F F F T F T T T T F F F T F T F For the first argument, the premises are all true only in row 1, and the conclusion, Q, is also. For example, the compound statement P → (Q∨ ¬R) is built using the logical connectives →, ∨, and ¬ The truth or falsity of P → (Q∨ ¬R) depends on the truth or falsity of P, Q, and R A truthtableshows how the truth or falsity of a compound statement depends on the truth or falsity of the simple statements from which it’s. Show that $(p \implies q) \wedge (q \implies r) \implies (p \implies r)$ is a tautology I have the truth tables but cannot algebraically manipulate the language itself to prove it Proving hypothetical sylloligism (p implies q, q implies r, therefore p implies r) with boolean algebra 1 Show that $(p \to q)\land(q \to r)\to (p \to r)$ is.
P = "" Q = "" R = "Calvin Butterball has purple socks" I want to determine the truth value of Since I was given specific truth values for P, Q, and R, I set up a truth table with a single row using the given values for P, Q, and R Therefore, the statement is true. If Q then R Again this is because the first is always true when P is false, but choosing Q and R appropriately makes the second false Also, you are very confused about logic An implication of the form "P implies Q" has absolutely nothing to do with "P iff Q", so it makes no sense to talk about equality For now, make sure you understand the truth tables of all the logical. It is convenient to read → sentences in English using if then That is, we read P → Q ( “P arrow Q”) as if P, then Q But there are many other ways in English of saying the same thing, and hence many other ways of reading → sentences in English Q if P P only if Q Q provided that P Q in case P Provided P, Q In the event that P, Q.
P ^ q !. 2 then (p 2)2 > (3 2) 2 We know that p 2 > 3 2 Therefore, (p 2)2 = 2 > (3 2) 2 = 9 4 Is the argument valid?. P q r q p r ∴ q aka Disjunction Elimination Corresponding Tautology ((p q) ∧ (r q) ∧ (p r )) q Example Let p be “I will study discrete math” Let q be “I will study Computer Science” Let r be “I will study databases” “If I will study discrete math, then I will study Computer Science”.
A Inverse statement B Contrapositive Statement C A syllogism D Converse statement Other questions on the subject Mathematics Mathematics, 1840, miguel3maroghi Some boys and girls were asked if they had a pet one third of the group were boys there were boys % of. If p = q and q = r then p = r What statements is this?. P only if q means "if not q then not p, " or equivalently, "if p then q" Biconditional (iff) The biconditional of p and q is "p if, and only if, q" and is denoted p q It is true if both p and q have the same truth values and is false if p and q have opposite truth values Sufficient condition p is a sufficient condition for q means "if p then q" Necessary condition p is a necessary condition for.
And the conclusion is~r We then create truth. Valid argument forms alwaysproduce valid arguments irrespectiveof the propositions chosen to replace the variable letters used in the argument form This leads to the following definition DefinitionLet p, q, r,etc stand for propositions An invalid argument formis an argument given in terms of p, q, r, such that the resulting argument may be invalid or may be. Therefore if p is true then q and r are true ∴ (¬p∨¬q) e negation of (p and q) is equiv to (not p or not q) Ô.
If p then q p Therefore q eg All humans are mortal Socrates is a human Therefore, Socrates is mortal 2 Modus Tollens (“Method of denying”) If p then q ~q Therefore ~p eg All humans are mortal Zeus is not moral Therefore, Zeus is not a human • Exercise Section 23, #26, 27, p 62. If P, then Q Therefore, if not P, then not Q which may also be phrased as → (P implies Q) → (therefore, notP implies notQ) Arguments of this form are invalid Informally, this means that arguments of this form do not give good reason to establish their conclusions, even if. R When in doubt, use parenthesis c Xin He (University at Buffalo) CSE 191 Discrete Structures 19 / 37 Translating logical formulas to English sentences Using the above logic operators, we can construct more complicated logical formulas (They are calledcompound propositions) Example Proposition p Alice is smart.
(p → q) (p → r) ∴ (p → (q∧r)) if p then q;. The argument form "If p, then q q Therefore, p" is Invalid An argument intended to provide probable support for its conclusion is Inductive This argument—"If Buffalo is the capital of New York, then Buffalo is in New York Buffalo is in New York Therefore, Buffalo is the capital of New York"—is an example of. And if p then r;.
So, when P is indeed true, so is Q The combinationof P is true with Q is false DOES NOT OCCUR Since this is the only time"if P then Q" is false, we know that "if P then Q" is true The sentence "If (if P, then Q) and (if Q, then R), then (if P, then R)" captures the. Therefore if p is true then q and r are true De Morgan's Theorem (1) ¬ (p ∧ q) ├ (¬p ∨ ¬q) The negation of (p and q) is equiv to (not p or not q) De Morgan's Theorem (2) ¬ (p ∨ q) ├ (¬p ∧. ( ( p > q ) ^ ~p ) > ~q is not a tautology (it is false when p is false and q is true) Begging the question or circular reasoning occurs when one or more steps of a proof are based on the truth of the statement being proved Methods of Proof of an Implication Generally, we will be solving problems of the form, ``If p, then q'' where p.
Click here👆to get an answer to your question ️ Given that P = Q = R If vec P vec Q = vec R then the angle between vec P and vec R is theta1 If vec P vec Q vec R = vec 0 then the angle between vec P and vec R is theta2 The relation between theta1 and theta2 is. R = you get ahead in life Premise 1 p → q Premise 2 q → r Conclusion p → r Thus, the argument converts to ((p → q) ∧ (q → r)) → (p → r) ' 05Œ09, N Van Cleave. The argument is valid modus ponens inference rule We cannot conclude that the conclusion is true, since one of its premises, p 2 > 3 2, is false Indeed, in this case the conclusion is.
11 PROPOSITIONS 8 “if 4 = 7 then London is in Denmark” (false → false) However the following one is false “if 2 < 4 then London is in Denmark” (true → false) In might seem strange that “p → q” is considered true when p is false, regardless of the truth value of qThis will become clearer when. ===== If P, then Q If Q, then R Therefore, if P, then R ===== P → Q Q → R P → R 1 Disjunctive Syllogism (DS) Either Ralph walked the dog or he stayed home Ralph did not walk the dog Therefore, he stayed home ============================== Either P or Q Not P Therefore, Q ============================== P v Q ~P Q 1. P q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18 (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a.
1 q e 2 2 2q er r) 2 = q2e 1 1 q 2e 2 2 q er r Therefore every prime in the prime factorization of n is raised to an even exponent Conversely suppose that every prime in the prime factorization of n is raised to an even exponent Then n = p2k 1 1 p 2k 2 2 p 2kr r where p i are primes and k j are positive integers Let m = pk 1 1 p k 2 2 p kr. 1 If P then Q 2 P 3 Therefore, Q Valid (Modus Ponens) Notice that this argument is still valid even though (as far as we know) all the premises (and the conclusion) are, in fact, false F 1 If P then Q 2 Q 3 Therefore, P Invalid This is the same invalid form as argument B Notice that all the premises and the conclusion are in fact true. In propositional logic, modus tollens, also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference Modus tollens takes the form of "If P, then Q Not Q Therefore, not P" It is an application of the general truth that if a statement is true, then so is its contrapositive The form shows that inference from P implies Q to the.
A valid argument form made up of three hypothetical, or conditional, statements If p, then q If q, then r Therefore, if p, then r Independent Premise A premise that does not depend on other premises to provide support to a conclusion;. QUESTION 67 If p then q r Therefore q O A Valid, affirming the antecedent O B Invalid, fallacy of denying the antecedent O C Invalid, fallacy of uncertain relation. If the hypothesis p of an implication p ® q is false , then p ® q is true for any proposition q Prove that Rt(2) is irrational Solution Since p 2 is an even integer, p is an even integer \ p= 2m for some integer m \ (2m) 2 = 2q 2 Þ q 2 = 2m 2 Since q 2 is an even integer, q is an even integer \ q= 2k f or some integer k.
Ment which asserts that if pis true, then q is also true We agree that p!qis true when pis false The statement pis called the hypothesis of the implication, and the statement qis called the conclusion of the implication Therefore (p_q) is the same as 4 CHAPTER 1 LOGIC p^q Using the same reasoning, or by negating the negation, we can see. If p, q are statements, their conjunction is the statement "p and q" It is denoted p ∧ q For example, let p be the statement "I have a dime" and let q be the statement "I have a nickel” Then p ∧ q is the statement "I have a dime and I have a nickel" In general, in order for any statement of the form “p ∧ q” to be true, both p. If p or q, then r Therefore, if not r, then not p and not q Practice Exercises Compound Statements use the symbols (logical AND), (logical OR), and ~ (NOT) to build complicated logical statements out of simpler ones Let p = "It is hot" and let q = "It is sunny" Then the statement "It is not hot but it is sunny" can be written symbolically as.
The first step in investigating possible implicit premises is to a Search for a credible premise that would make the argument as strong as possible b Rewrite the argument c Search for a credible premise that would make the argument valid d Make a bad argument good Modus ponens has this argument pattern. And if p then r;.
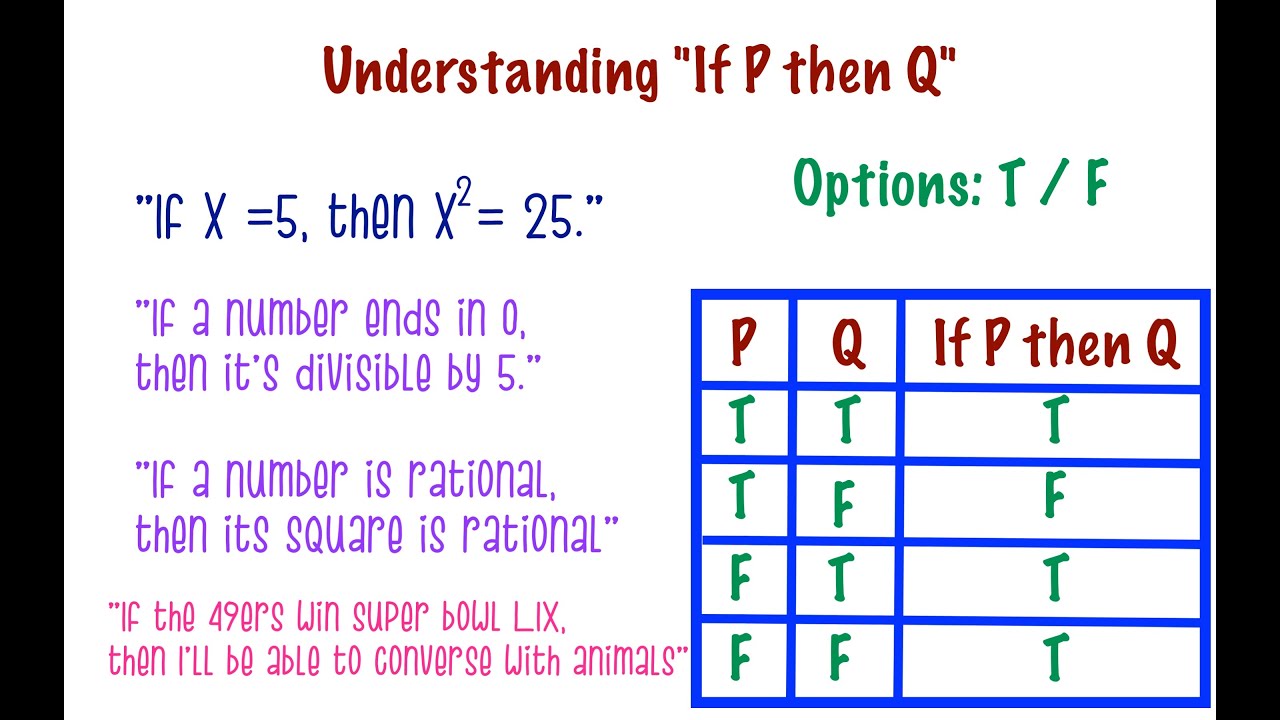
Understanding If P Then Q Youtube

Affirmingte Conseouent In Your Textbook Thinking Critically Page

Formal Logic The Propositional Calculus Britannica
If P Then Q If Q Then R Therefore If P Then R のギャラリー

Logic Ch 7 Flashcards Quizlet

Artificial Intelligence Predicate Logic Dr Anna Fensel
Alyve Org

Ques 25 Mcq The Lcm Of Two Prime Numbers P And Q P Q Is 221

Section Three Using Deductive Reasoning To Verify Conjectures Sushi Ya S Math And Stuff

Logic Propositions N N A Proposition Is A

La Imagineria Mental Como Epifenomeno De Los Procesos Cognitivos Estudyando

The Resultant Of Two Vectors P And Q Is R If Q Is Doubled The New R Askiitians
1

Solved If Pete Is Correct Then Sam Is Wrong It Is Not The Chegg Com

Deductive Versus Inductive Reasoning Pdf Free Download

Cse261 Chapter1 Flashcards Quizlet

Review Chapter 8 Deductive Reasoning Deductive Logic Classical By Putting In Proper Form We Will Force Conclusion Standard Form Putting Things In Ppt Download
If 1 P Q 1 R P 1 Q R Are In Ap Then Sarthaks Econnect Largest Online Education Community

Premise Indicators Conclusion Indicators Indicators Therefore If And Only If Argument Using The Suggested Letters To Represent Propositions And Then Pdf Document

Solved Example Student Cannot Join The Overseas Exchange Scheme Unless He Or She Gets Gpa 3 0 Only If A Student Works Hard Then He Or She Can Get Gpa 3 0 Ic Student Receives
Plp Earcqizcdm
The Principles Of Projective Geometry Applied To The Straight Line And Conic F P Ar And Br Must Pass Through Q And Y Re Spectively Therefore Qp Is The Polar Of

Progressives And The Church On Justice La Progressive

Pdf Tutorial On Rational Rotation C Algebras
Arxiv Org

If P Rarr Q Vee R Is False Then The Truth Values Of P Q R Are Respectively Youtube

Evolution Of Cognition Aimed At Seizing Up The Prezentaciya Onlajn
How To Prove The Theorem If P Then Q Implies R Is There More Than One Proof Method That Can Be Used Quora

Cookie Policy This Website Uses Cookies To Ensure You Get The Best Experience On Our Website Learn More Declineallow Cookies Studylib Documents Flashcards Chrome Extension Login Upload Document Create Flashcards Login Flashcards Collections

Common Valid Deductive Forms Dilemma P Or Q If P Then R If Q Then S Therefore R Or S Example Either George W Bush Will Win The Election Or John Kerry
1

Ppt Apologetics Logic And Reasoning Powerpoint Presentation Free Download Id
1
Argschemes Overview
Math Colostate Edu

Truth Tables The Conditional And The Biconditional Implies And Iff Mathbootcamps

Philosophy 103 Linguistics 103 Yet Still Even Further

How Does If P Then Q Have The Same Meaning As Q Only If P Mathematics Stack Exchange

Chapter 22 Common Propositional Argument Forms Introductory Remarks P 2 This Chapter Introduces Some Of The Most Commonly Used Deductive Argument Ppt Download
An Elementary Treatise On Coordinate Geometry Of Three Dimensions Torsion Again Tan 6 A And Therefore 0 Is Constant 0 1 Rip This Problem Was First Investigated By

Adaptive Two Stage Designs For Single Arm Phase Iia Cancer Clinical Trials Lin 04 Biometrics Wiley Online Library

Phil 1290 Chapter 03 Practice Quiz Phil 1290 Critical Thinking U Studocu

Introduction To Logic Pdf Free Download

Math Discrete Maths Pdf Syntax Logic Logic

Solved Valid Or Invalid O 1 If P Then Q If R Then Q P Chegg Com

Ppt Deductive Validity Powerpoint Presentation Free Download Id

Logic And Proof Argument An Argument Is A Sequence Of Statements All Statements But The First One Are Called Assumptions Or Hypothesis The Final Statement Ppt Download

Formal Logic The Propositional Calculus Britannica
Lume Ufrgs Br

Solved Propositional Logic F 48 P A Q Q R L If Q If P Chegg Com
Conditional Statement

Pdf The Elusive Oddness Of Or Introduction Semantic Scholar

Two Forces P And Q Act Such That The Resultant R Is Equal To P If P Askiitians

15 Logic Engineering Mathematics Volume I Second Edition Dev Guis
Agloa Org
Osti Gov

Modus Tollens Indirect Droon Q P Q Pshow Th Itprospt

Doc A Rulebook For Arguments Savannah Annika Maglasng Academia Edu

Propositional Logic Conditional Statement If P Then Q
Jstor Org

If P Q And R Are In Ap Then Prove That Left P 2q Rright Left 2q R Pright Left R P Qright 4mathit Pqr Snapsolve

Arguments Introduction To Philosophy Handout Phil 100 Docsity
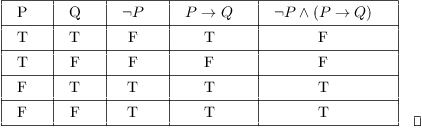
Truth Tables Tautologies And Logical Equivalences

Philosophy Logic And Logical Arguments Ppt Video Online Download

End Of Chapter 3 Critical Thinking

Chapter 3
Symbolic Logic 3 Testing Deductive Validity With Truth Tables For An

Phil 210 Course Notes All Chapters Phil 210 Critical Thinking Studocu

Premise Indicators Conclusion Indicators Indicators Therefore If And Only If Argument Using The Suggested Letters To

Rules Of Logical Inference Pdf

If P Q R Is False Then The Truth Values Of P Q R Are Respectively
Know Your Logical Proofs Smbc R Comics

Children S Ability To Handle Piaget S Propositional Logic A Conceptual Critique Semantic Scholar

Chapter 2 The Logic Of Compound Statements Flip Ebook Pages 1 13 Anyflip Anyflip

Negating The Conditional If Then Statement P Implies Q Mathbootcamps
Wiki Eclipse Org

Phi 1101 Lecture Notes Fall 14 Lecture 15 Modus Tollens Modus Ponens Hypothetical Syllogism

Un Ejemplo De Esta Falacia Podria Ser El Siguiente Pdf Descargar Libre

Solved Consider The Following Sentences A If P Then Q Chegg Com
Solved Determine Whether The Argument Form Is Valid Or Invalid Course Hero

Phil 1290 Chapter 03 Practice Quiz Answers Phil 1290 Critical Studocu

Phi 1101 Study Guide Fall 13 Final Cephalus Deductive Reasoning Presupposition

Logic Of Compound Statements Discrete Mathematic Handout Math 245 Docsity
Degruyter Com
Propositional Logic Conditional Statement If P Then Q

Logical Implication Rules Of Inference The Following Section Will Now Do A Formal Study Of What An Argument Is And When An Argument Is Valid This Will Help Investigate How To Prove Theorems In Later Sections Definition Of An Argument And Valid Argument

Know Your Logical Proofs 9gag

03 Ethics Pt 2 Modus Ponens Modus Tollens Hypothetical Syllogism Youtube
Link Springer Com

Rhetorical Devices And Logical Fallacies Rhetorical Devices

2 3 Methods Of Proof Ppt Video Online Download

Ppt Propositional Logic Powerpoint Presentation Free Download Id

1iqq8 85 Bpsxm
The Argue Mentor

Nn Range And Mss Queries Case 2 If There Are Multiple Nearest Download Scientific Diagram
Academic Oup Com

Doc Inference Rules Jorenz Undag Academia Edu
Truth Tables Tautologies And Logical Equivalences

Solved If Or Stands For Disjunction And For Conjunction Not For Negation And Implies For Implication Then Match The Following Names Of Valid Argument Forms With Their Symbolic Forms Or Q Not P

Answered Let P 2 Is A Factor Of N Q 3 Is Bartleby

Decentralized And Open Thinking Part 1 Speaker Deck

Philosophy 103 Linguistics 103 Yet Still Even Further

Material Conditional Wikipedia
Show By Constructing Annotated Derivations That The Following Arguments Are Valid 1 Fall Ra Q Prrj 2 Piq R Q Hms S S Mspo Course Hero

Please Answer Just Like The Picture Exercise 4 1 For Each Of The Following Arguments Determine Whether Homeworklib




