円 面積 積分
以上の考え方は、「円を無限に細かく分割できること」を前提とした考え方のため、直感的にはイメージできても正確な計算にはなっていません。 円の面積は、正確には『 積分 』というテクニックを使うことで以下のように求められます。 積分については、以下の記事で解説しています。 積分とは何なのか? 面積と積分計算の意味 積分とは「微分の反対」に相当する操作で、関数 f ( x).
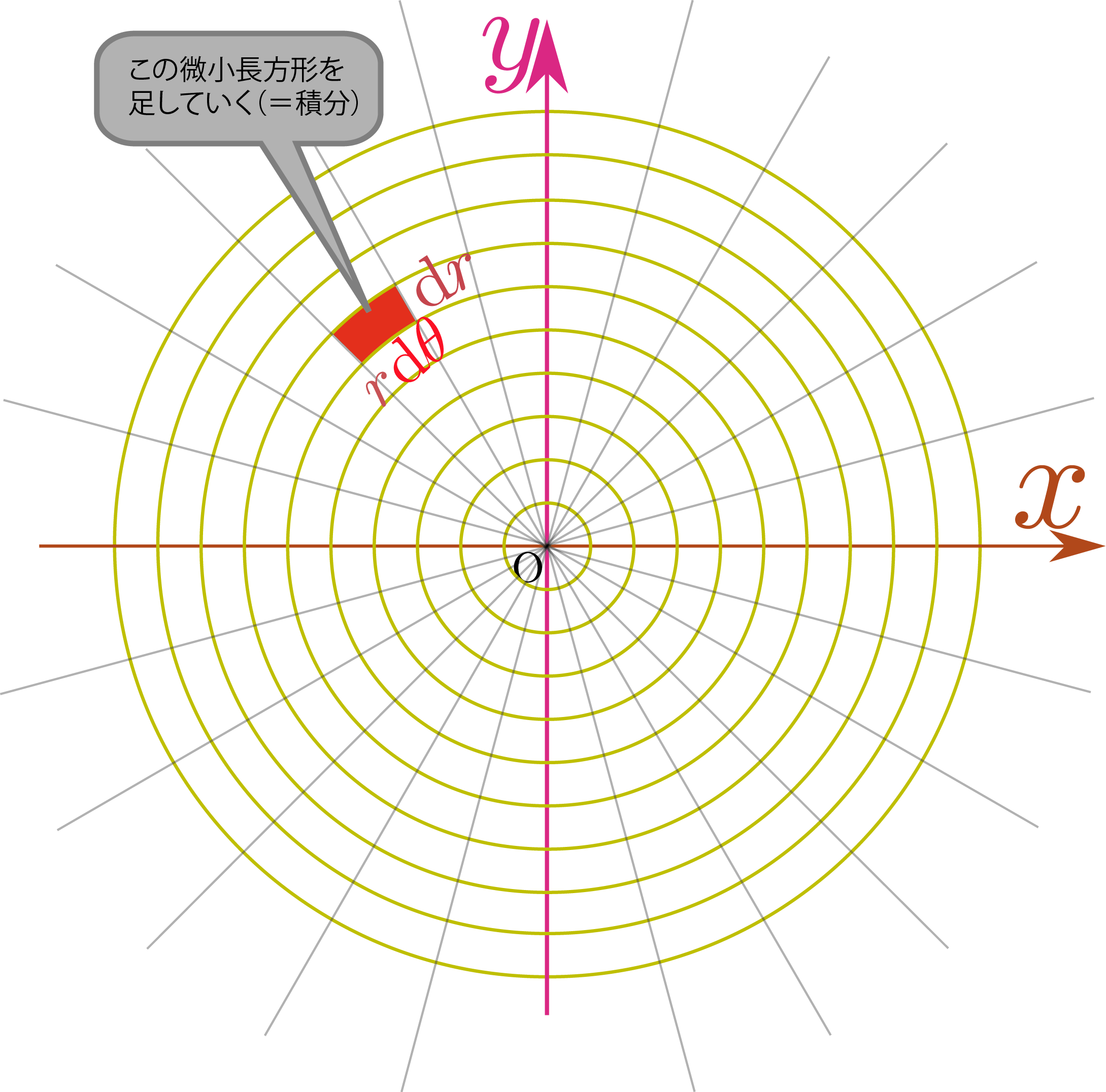
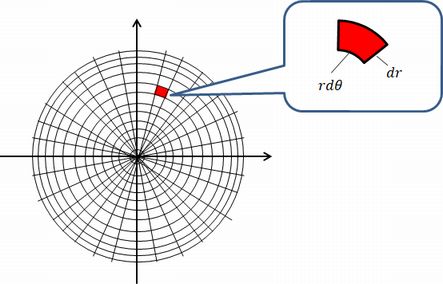
円 面積 積分. 円の面積 複雑でよく間違える計算なので助かった。 食卓を買い替えるにあたり、丸ちゃぶ台サイズ90φか100φかかなり悩みました。 いっそ間をとって95φもありかなと思ったり。 ちなみに現テーブルは長方形90×60。 夫が現テーブルを手狭に感じている. 円の面積を求める方法の1つに、2次元極座標で 方向と 方向の格子に分割して、 を計算する方法がありますよね。 この場合、積分する微小領域の形を縦と横が と の長方形とみなして、その積 をその面積としていると見なせます。 しかし微小領域は厳密に. 表面積を求める公式 S = r π (r m) S = r π (r m) 母線をm, 半径をr, 高さをhとすると表面積はこのようにあらわされます. 円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります..
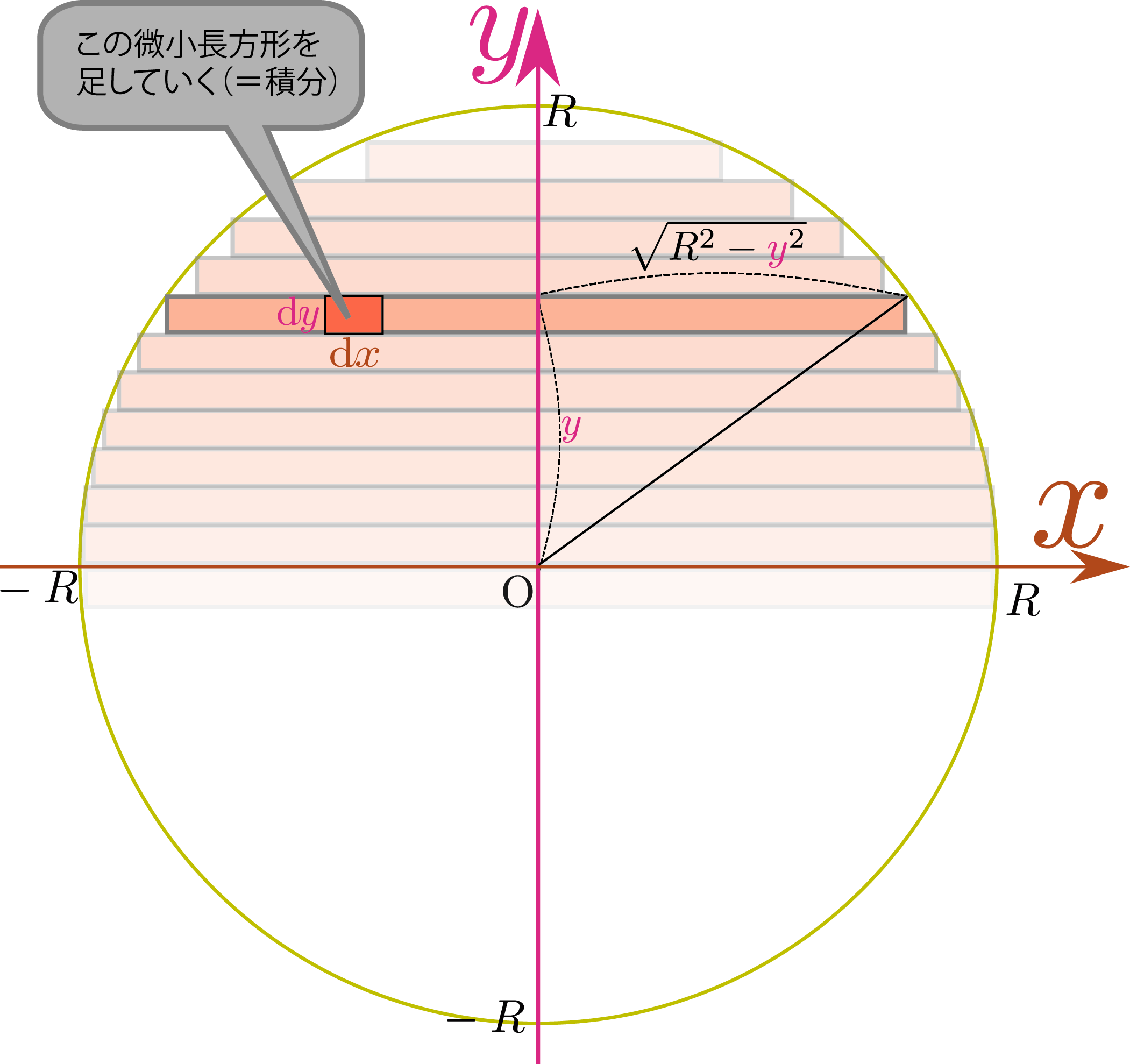
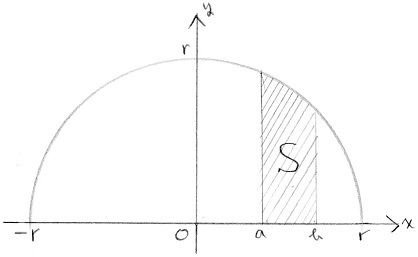
円の面積を計算するには、微小面積 dxdy を積分(足算)する。 どのような範囲で積分するかが重要で、右のように円を設定すると、ある一つの y の値に対して x = − √R2 − y2 から x = √R2 − y2 までの範囲で足算し、次に y = − R から y = R までという足算をすればよい。 具体的な積分は以下の通りで. 底面の円の直径方向に座標軸 をとり, の範囲で断面を求めて積分する. 底面の円に描いた黄色の直角三角形で,斜辺の長さは半径 に等しいから, 次に高さ は, のとき で傾きが の直線上にあるから, ここで は奇関数の積分だから0 は上半円の面積だから. 左図において、1辺が a の正方形の面積は、 である。 逐次積分の計算例1 円の内部及び周 x 2 +y 2 二重積分 を計算せよ。 (解) (終) 値が 0 になることは、グラフからも推察される。 逐次積分の計算例2 二重積分 を計算せよ。.
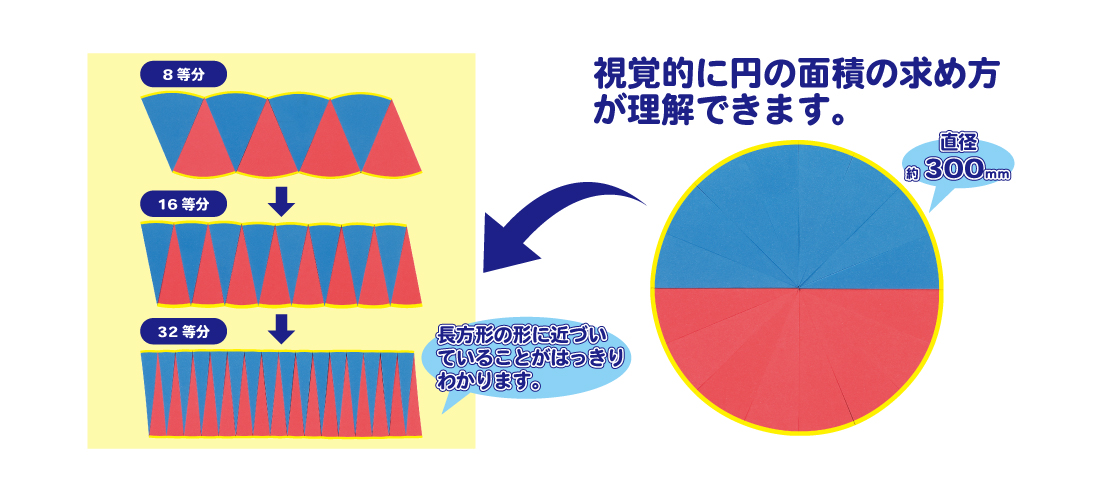
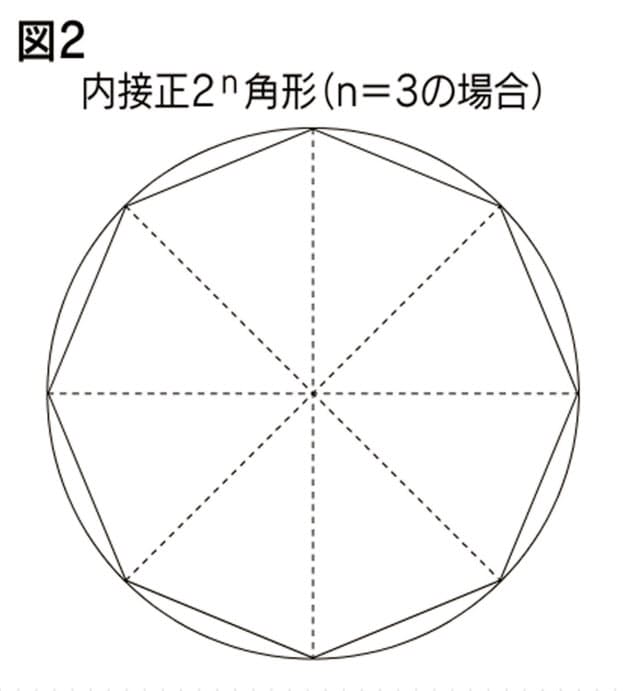
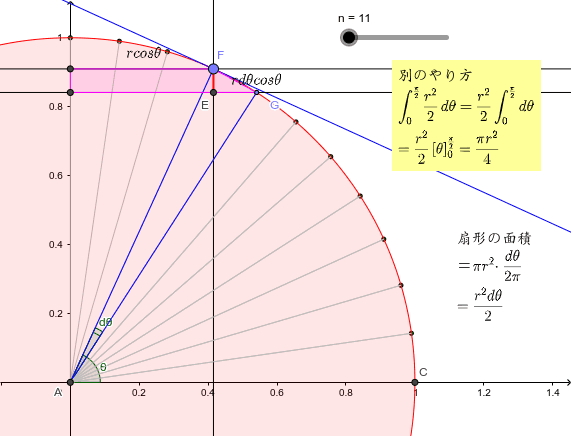
「微分・積分」の勉強 (1)積分: 以下の問題を考えます。 問題 半径 1 の円の面積Sをπと定義する。 面積S=π この面積Sを求めよ。 (解答) この問題は、以下の様に解くことができます。 円を、以下の図の様な短冊に分割し、 その. 円の面積( S urface area) π 円周率(= 314) r 円の半径( r adius) 公式の導き方のイメージ この円の面積を求める公式は、円を無限個の扇形に分け、それを長方形につなぎ変えることで導くこと. 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの.
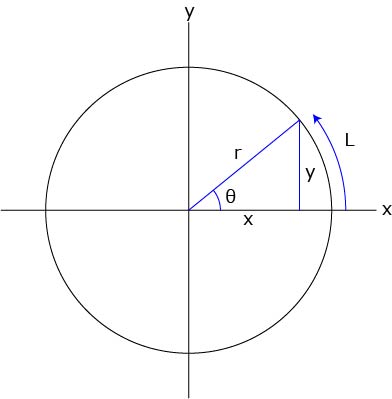
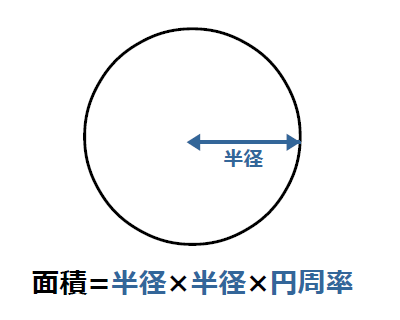
円を直線で切った時の面積の計算方法を教えてください。 半径rの円の一番底からHの高さで直線で切った時の面積を計算する方法を教えてください。rとHだけの式でできるでしょうか? 図のように線を引き、 OABを定めるOA=rhとなるので、三平方の定理より、AB=√(2rhh^2)また、∠AOB=θとおくと. と円の面積が求まりました。 面積は積分によって定義されますが、積分の計算は「微分の逆」として行えます。 微積分学の基本定理として知られる素晴らしい発見で、面積の話とセットで微分が登場するのはそういう事情があるわけです。 参考: 積分とは何か? 面積を長方形で近似計算してみよう 次いで球の体積を求めてみます。 キャベツを輪切りにするようにして、できた輪の面. 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。 Tooda Yuuto 「なんでこんな公式になるんだろう? 」と思った方は、ぜひ「 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 」の記.
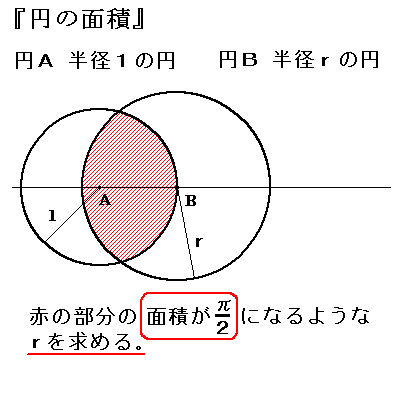
円筒の面積と、円の面積の違い 円筒の面積の面積と、円の面積の違いを下記に整理しました。 円筒の面積 ⇒ A=π×(ra 2 -rb 2 ) 円の面積 ⇒ A=π×r 2 円筒の面積は、中が空洞です。空洞部の面積を引いた値が、円筒の面積ですね。 まとめ. さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。. 円の面積を求める。半径a の円(の中身)は 2 < なので、この範囲で関数1を積分する。 𝐼=∫ 1 2 2< であるが、(これは簡単な例なのでこのままやってもできるけど、そうでなくて、) =𝑟 𝜃 𝑟 と置き換えて.
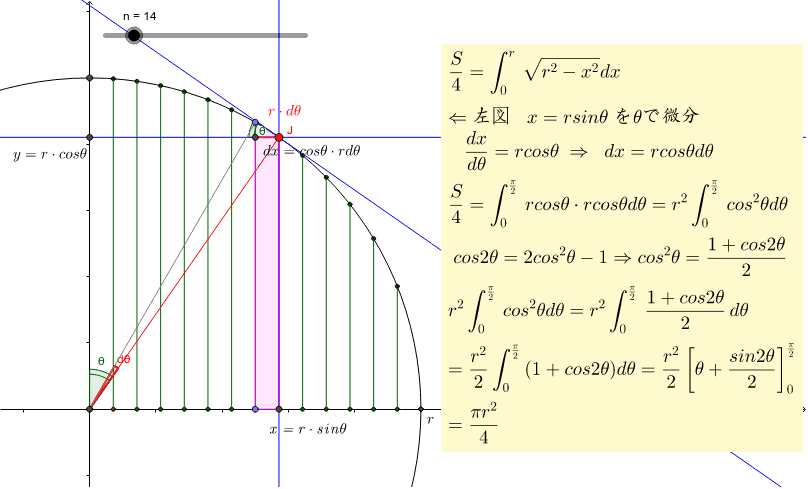
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ. 円の式: X2+Y2=1 → Y=(1-X2)1/2 積分式: S=4∫(1-X2)1/2dX(4分の1円の面積X4) ここで、積分の範囲は0から1までです。 極座標の変換式とそれを用いた円の面積の積分式は、 変換式: X=COSθ Y=SINθ 積分式: S=4∫(1-COS2θ)1/2 (-SINθdθ) ここで、積分の範囲はπ/2から0までです。 この積分は、次のように計算できます。 S=-4∫SIN2θdθ=-4∫(1-COS2θ) dθ/. これが円の面積を出す定積分です。 ∫rdr = (1/2)r² 0≦r≦aで (1/2)a² ∫dθ =θ 0≦θ≦2πで 2π よって、 (1/2)a²•2π=πa² x=asinθ、または、acosθとおかないと 面積にπの値がつきません、 だから、これ以外の置換はないと思います。 1人 がナイス! しています Yahoo!検索で調べてみよう sin 積分 sin 表 sin 計算 sin 値 sin.
面積分 dS z = f (x, y) z x y 領域 上で 関数 の積分を考える.f を微小領域に分解し,そのそれ ぞれの微小領域を底面とし高さ を持つ柱体を考える. f この柱体の(符号も込めた)体積は f dS 微小領域の面積を dS と書けば 面積要素 f dS. 1は積分を知らなくても理解できますが,円の面積公式は認めてしまいます。 残り2つは定積分を用いる方法です。 どちらも積分のよい練習問題です。 グラフの拡大を用いた楕円の面積公式の導出 曲線 f (x,Ay)=0 f (x,Ay) = 0 は f (x,y)=0 f (x,y) = 0 を y y 軸方向に \dfrac {1} {A} A1 倍に引き伸ばしたもの という定理を使います。 →関数のグラフの拡大・縮小の証明と例 証明 楕円の式:. 円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。 円の面積の積分を式で表してみると、 ∫√(r2-χ2)dx である。 この√の原始関数は何だろうか? どうもわからない。 では、球の体積の積分はどうだろうか? 球の.
y = √9− x2 y = 9 − x 2 とすると、 x2 y2 = 9 x 2 y 2 = 9 なので、これは、原点を中心とした半径3の円の一部を表しています。 なので、 0 0 から 3 3 まで積分するということは、この円の右上の部分である 1 4 1 4 を表しているので、 32 4 π 3 2 4 π となり、これを 8 3 8 3 倍して、楕円の面積が 6π 6 π とあることがわかります。 標準定積分の置換積分(三角関数:cosθ. すると円の面積 は となります。 よって求めたい円は面積と幅を掛け算して、 となります。 あとはこの円が高さ だけ集まっていることになりますので、体積 は 円柱の体積の公式である底面積×高さと一致することが分かります。 三角錐 次は下の図のような三角錐の体積 を求めてみたいと思います。 まず積分する方向を今回は 軸方向と決めたいと思います。 よって は0から1の範囲. 円をぐるっと 1 回転することでドーナツの形になる。 これを 円環体 と言う。 考え方としては,大きな円から小さな円の面積を引くことでドーナツの面積を求め,それを積分で積み上げることで体積を求めます。 x=t x = t として,式を変形します。 t t の.
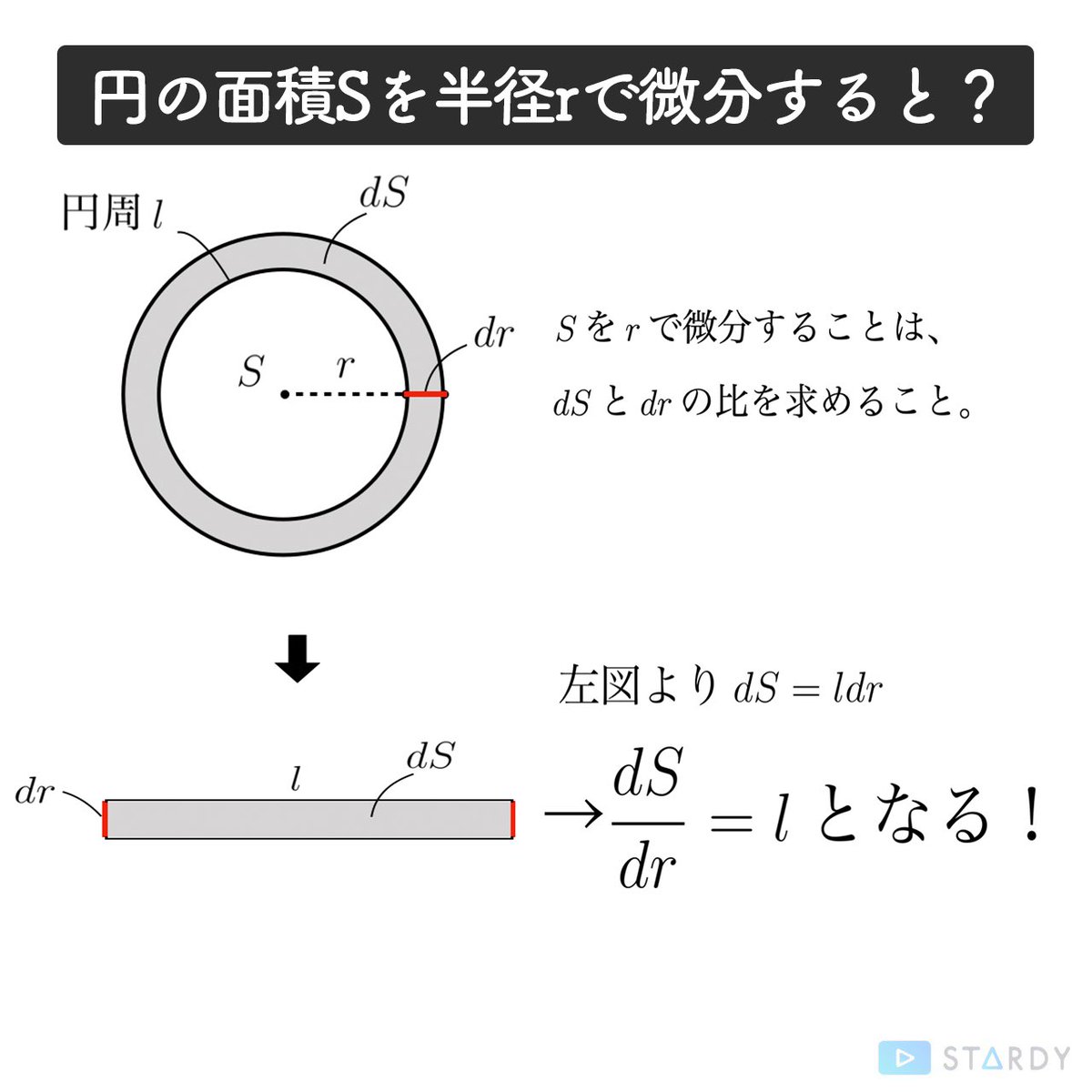
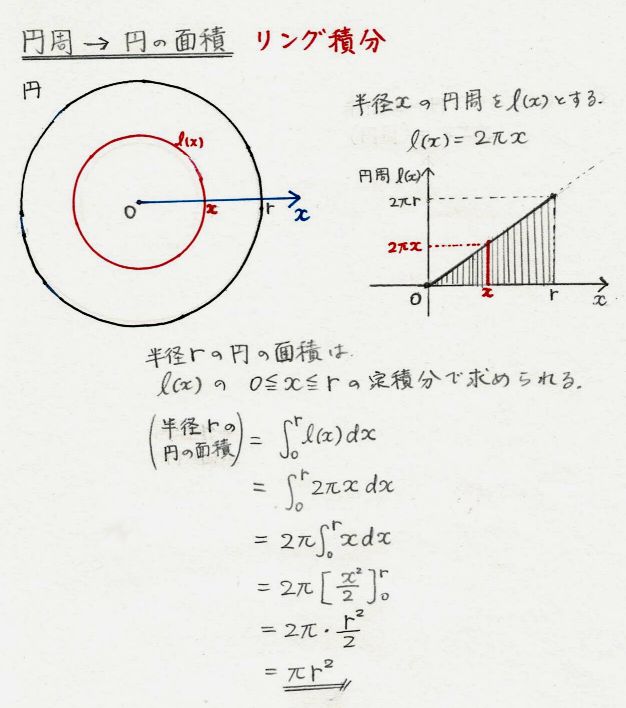
回転体の断面は必ず円となることから、どちらも 円の面積を積分する計算 になるのですね。 例題「曲線を x 軸周りに回転してできる立体の体積」 それぞれの公式を、例題で確認しましょう。 例題 次の曲線や直線で囲まれた部分を 軸の周りに 回転させてできる立体の体積 を求めよ。 (1) , , , 軸 (2) , (1) から順番に解いていきます。 まずは状況をグラフに整理し、回転させる平面を確認. 円の面積の関数 は微分すると円周になると言えるわけです (完璧さを求める方は の場合も考察してください。 以下の球の議論でも同様)。 言い換えれば、円の面積は円周 の積分 と計算できるのです。 円周の定義だけから円の面積が となることが導かれるんですね。 では今度は、同じ”ノリ”で球の体積 を微分してみます。 は球の体積の差で、下図の”厚みのある皮部分”の体積に相当. 前回にて線積分の概要と例題を取り扱った。 今回はその続きで、面積分の概要を眺め、問題の解き方を解説していく。概要 面積分も線積分と同様にベクトル場に対して実行する積分である。 線積分との違いは「面」と書かれている通り、ある座標系に存在する.
媒介変数表示されたグラフによって囲まれた面積の求め方は以下の3つの手順によって求めることができます! 媒介変数表示されたグラフの面積は、 1パラメータで微分してグラフの概形を描く 2積分の式を立てる 3パラメータで置換積分する という. 下のような 微分と積分の関係 が成り立ちます! くだけた表現をすると、 円周を 積分 = 円の面積 球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる 無限に薄く切った面を 足し合わせて立体をつくる という イメージ です. うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい.
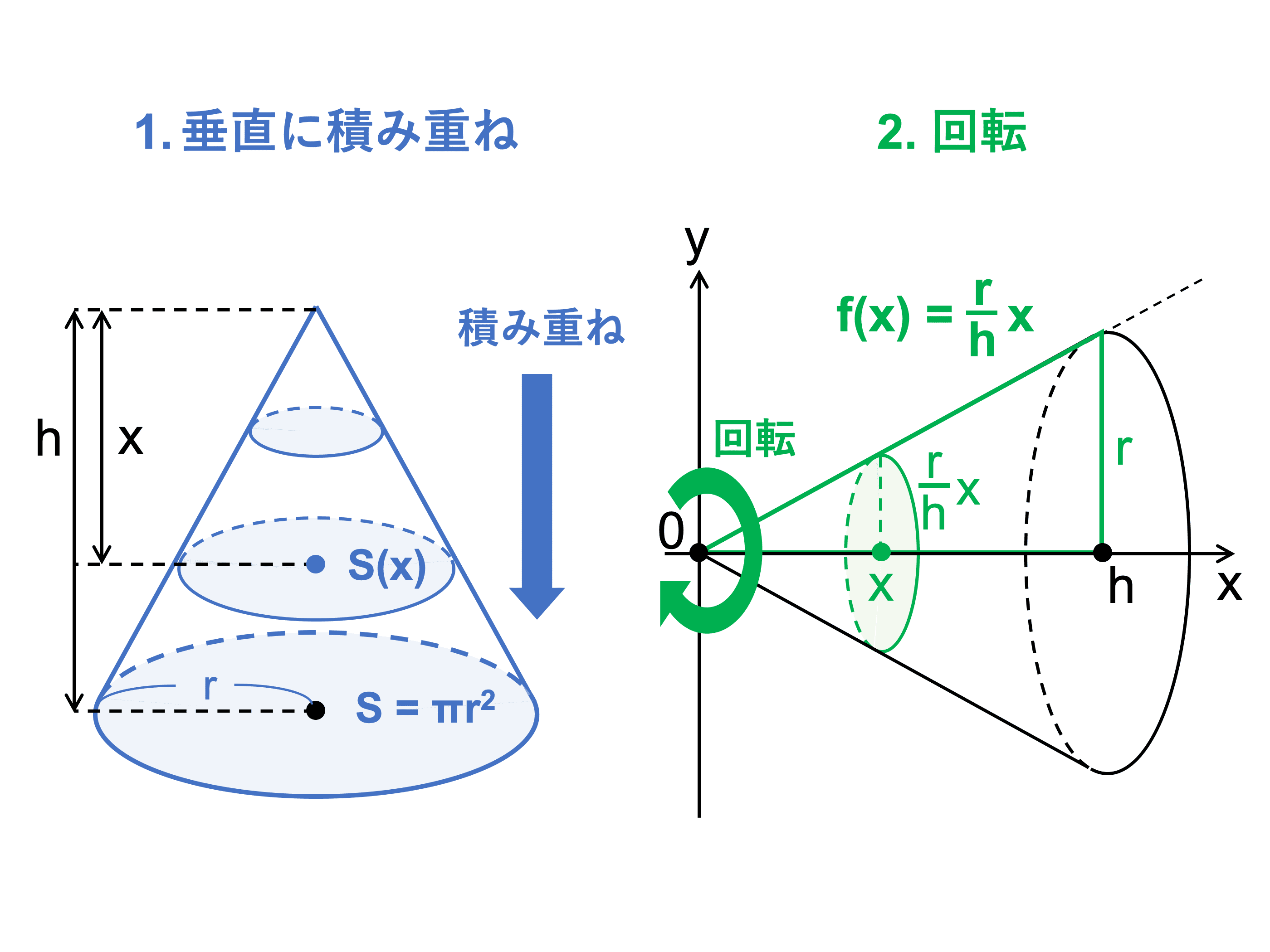
線積分 積分の概念を端的に表すと” 微小要素を足し合わせる ”ことであった 高校数学で登場する積分といえば 原始関数を求める か 曲線に囲まれた面積を求める ことに使われるのがもっぱらであるが, これらの応用として 曲線の長さを求める ことにも. 表面積を積分する(足し合わせる)と体積になる。 つまり、体積の微分が表面積。 (\displaystyle\frac {4} {3}\pi r^3)’=4\pi r^2 (34 πr3)’ = 4πr2 おまけ 円錐を積分で計算してみましょう。 底面の半径 r r 、高さ h h とする。 底面の中心を原点に、頂点に向かって軸を取る。 軸に平面に切る。 x x できった時、半径は \displaystyle\frac {r (hx)} {h} hr(h− x) となる。 (相似で求める).

積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張
تويتر Stardy على تويتر 実は円の面積を微分すると円周になると知っていましたか T Co Gisrglwseo
面積分
円 面積 積分 のギャラリー
2

Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 養成講座

高校生向け 積分 円の面積 Youtube

円 扇形 の面積 周や弧の長さの公式 数学fun

円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題
円の面積説明器 ヒシエス誠文社 ヒシエス誠文社

円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張

極方程式の面積 扇形積分 おいしい数学

円の面積応用b 学習ノート 学習 小学校 算数
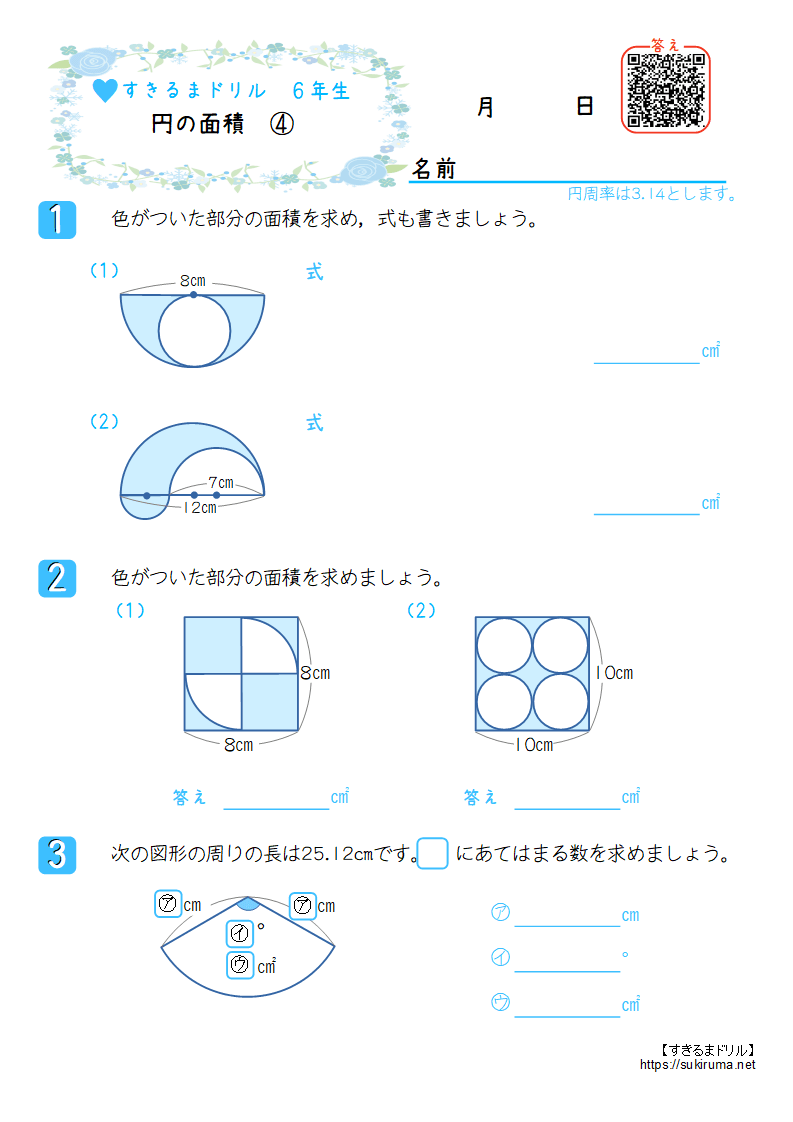
すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント
小6算数 円の面積 指導アイデア 1 みんなの教育技術
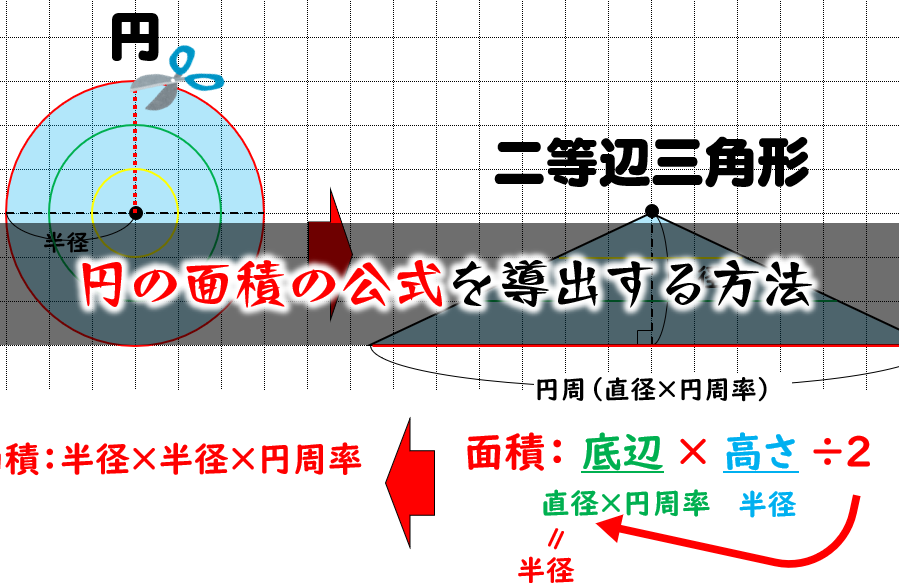
円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun

面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧
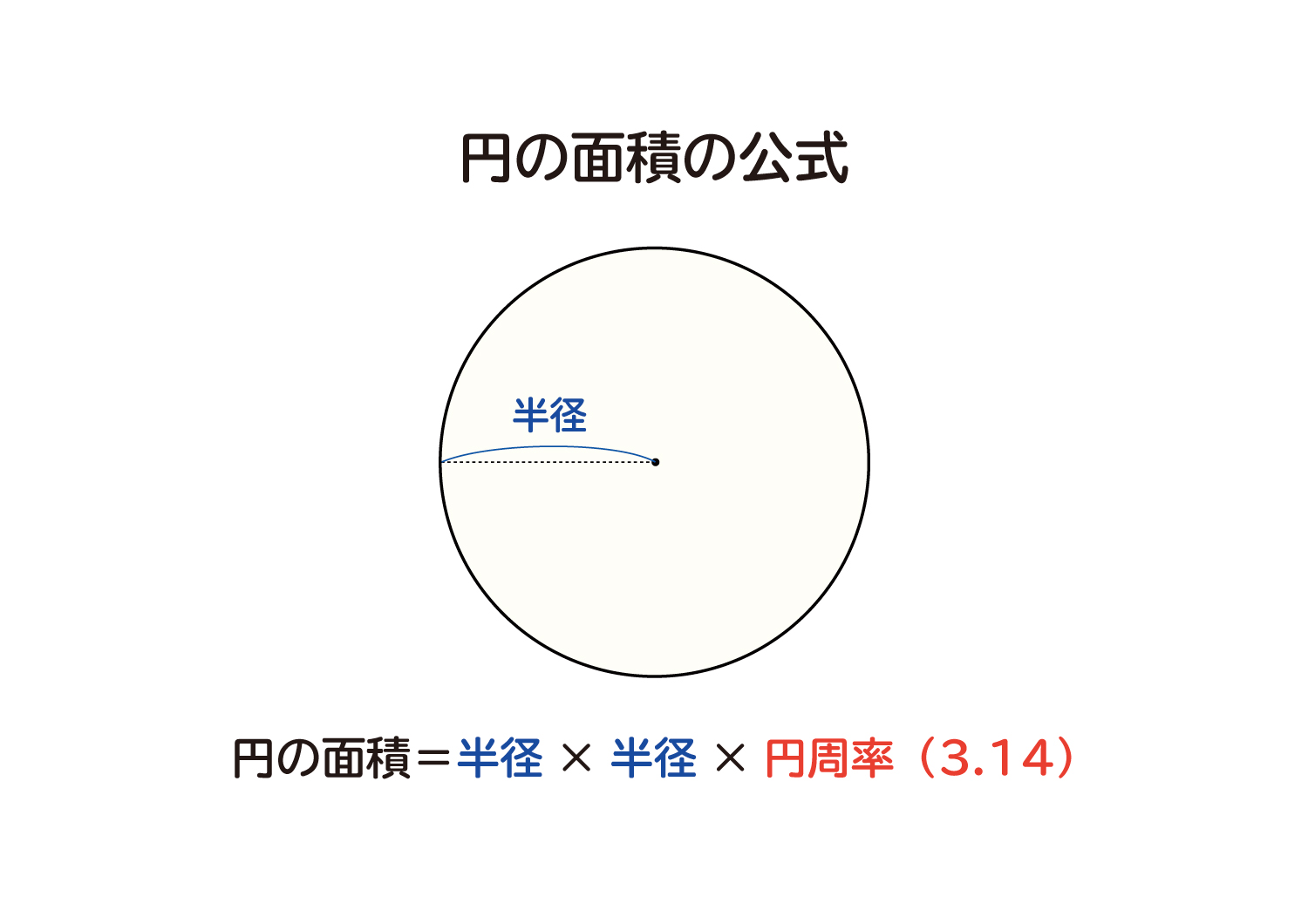
なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
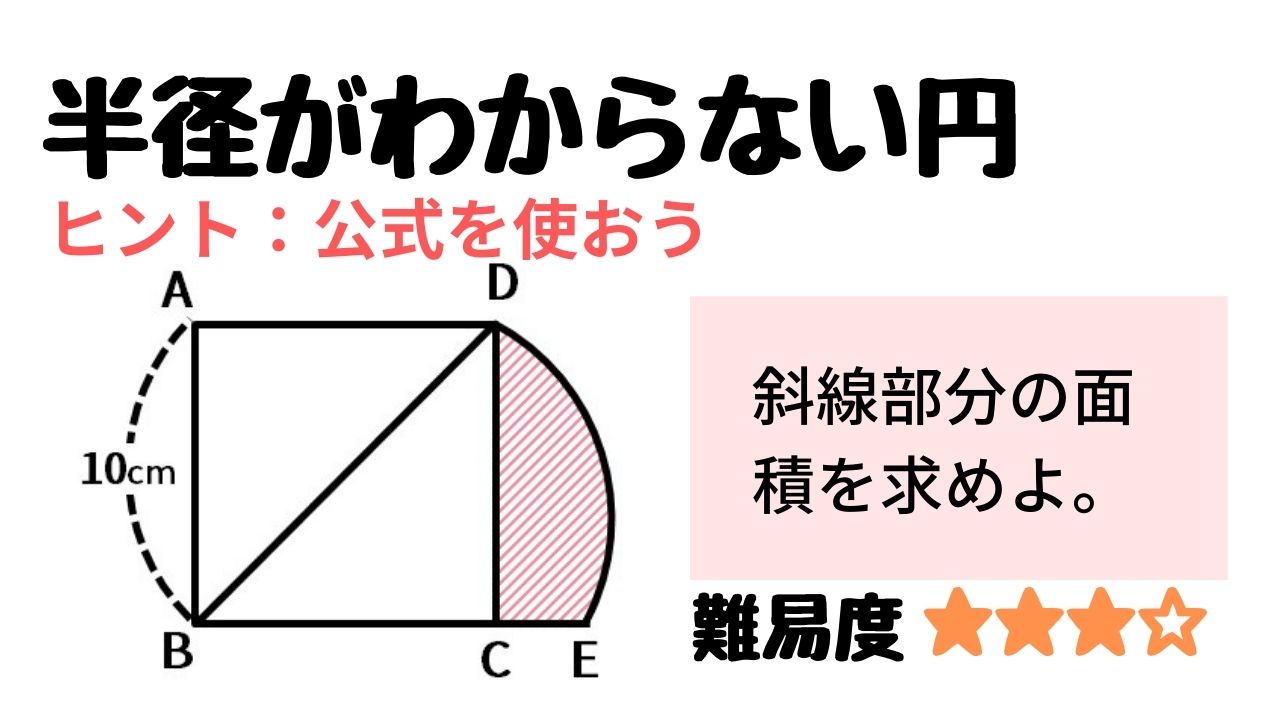
中学受験算数 半径がわからない円の面積の問題 テクニック伝授 Stupedia

数学 積分を使って面積や体積を計算する方法を分かりやすく解説
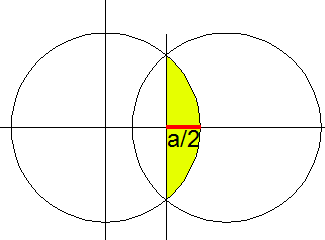
くろべえ 卵焼きの失敗と 2円の重なり部分の面積

アルゴリズム 2つの円の重なった面積 Teratail
面積分
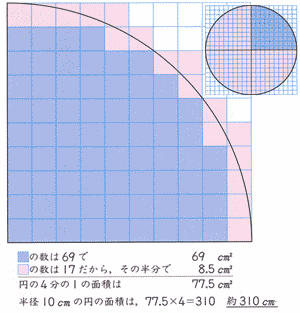
実践記録算数5年
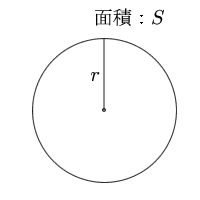
円 面積の計算 計算サイト
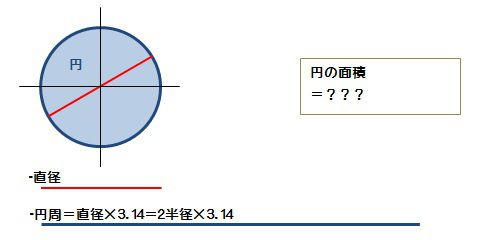
円の面積 算数の公式覚えてますか
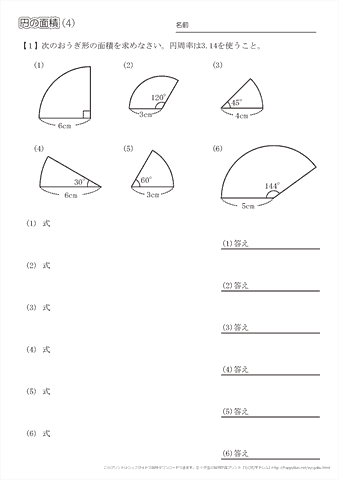
小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
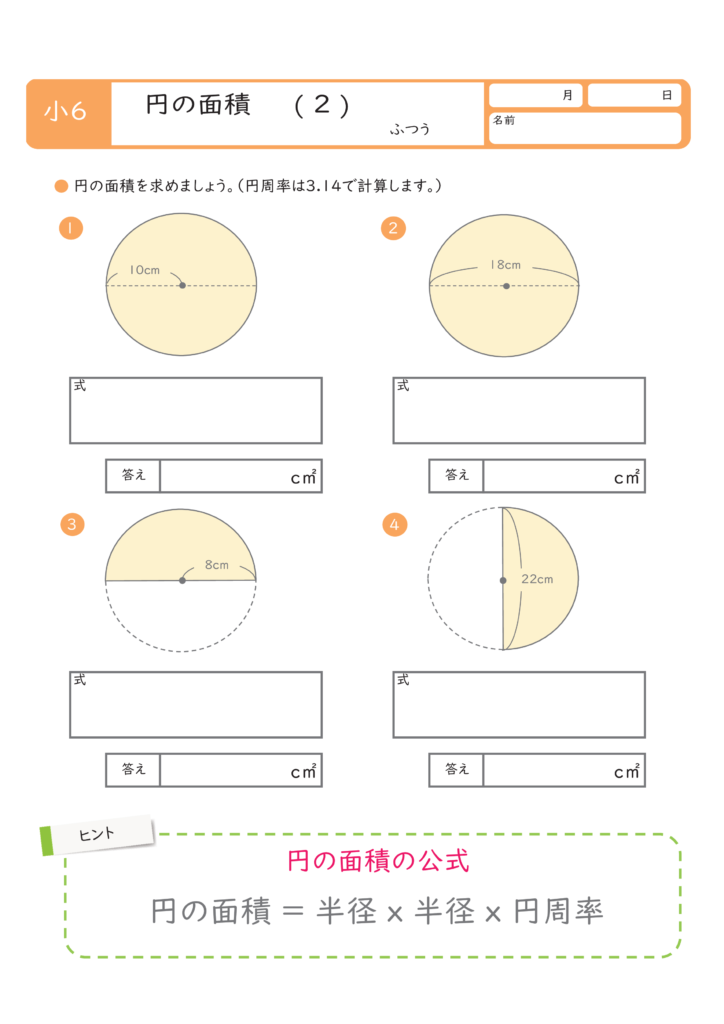
こどもプリント 円の面積 無料プリント
小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
電気磁気工学を学ぶ 積分と円の面積
円の一部の面積と 円の直径があり これらの情報から Xの距離を求 Yahoo 知恵袋
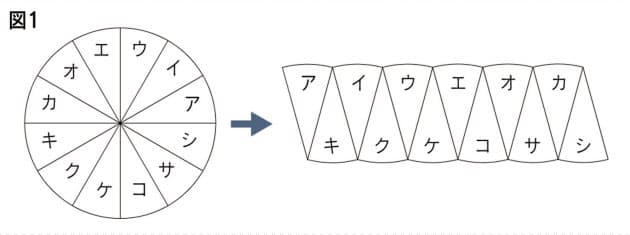
子供に説明できる 円の面積の公式 の証明 Nikkei Style
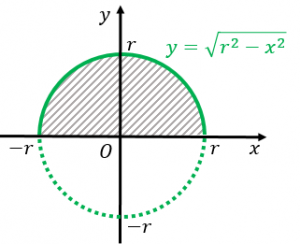
円の面積を積分で計算する2通りの方法 具体例で学ぶ数学
小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
Sphere 01

円の面積 算数用語集
子供に説明できる 円の面積の公式 の証明 Nikkei Style

File 円の面積 Png Wikimedia Commons
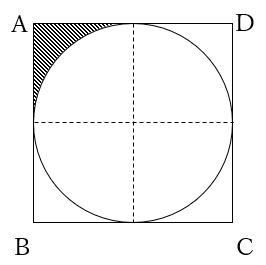
半径の分からない円の面積 中学受験プロ講師ブログ

6年算数 円の面積 3 わかる教え方のポイント

円の面積 Java実験室
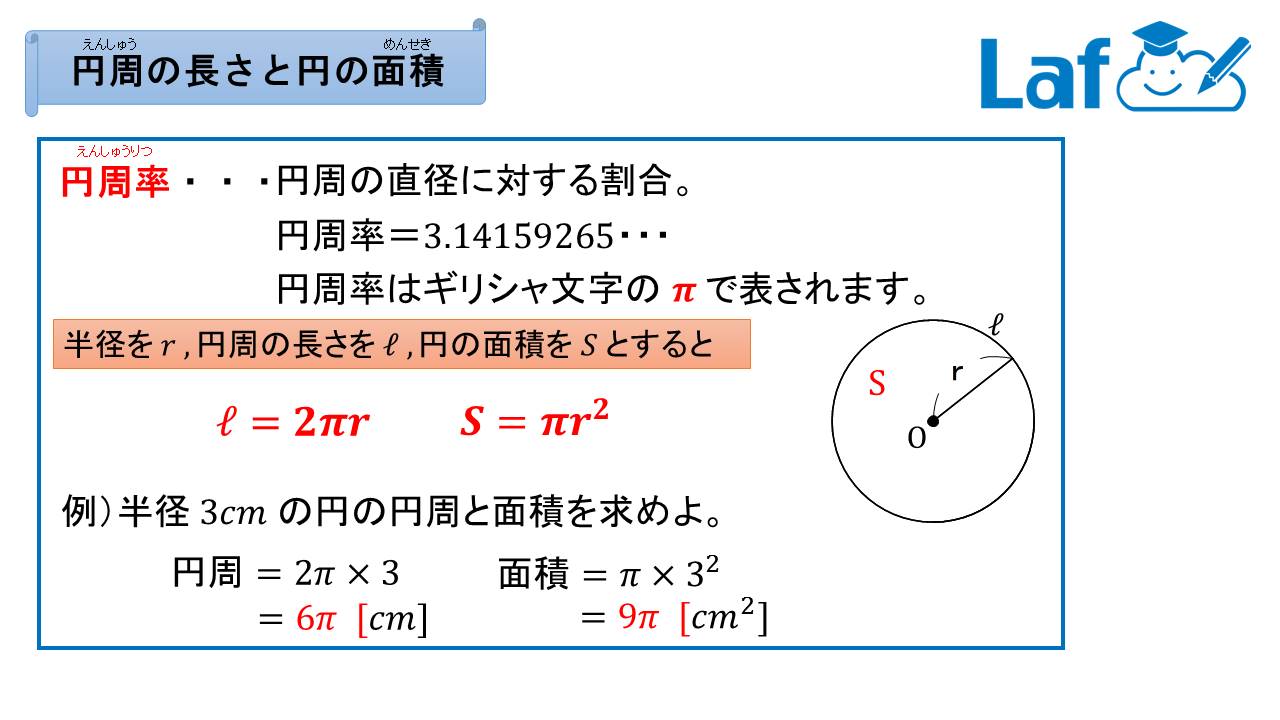
تويتر 中学高校数学laf先生 質問回答中 على تويتر 中1数学 円周率p 円の面積 円周の長さ 1年生は事前に知っておいて損はなし 2年生は今のうちに軽く目を通して思い出しましょう 3年生は知っていたらrt 3年生は覚えてなかったらふぁぼって

高校数学 楕円の面積と回転体の体積 受験の月
円と帯の共通部分の面積 Den Of Hardworking
円の面積計算 ゆるゆるプログラミング

高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット

6年 円の面積まとめプリント ネコ好きな学校の先生の日常
極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート

円の面積の公式 算数の公式
小学6年生 算数 無料問題集 円の面積 おかわりドリル

楕円で 円の面積の公式がそのまま出てくる理由がわからないです 赤線部分の説明 Clearnote

楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ

球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave
円の面積2 Geogebra
勉強しよう数学 円の面積を積分で求める

円の面積の求め方 公式と計算例

6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
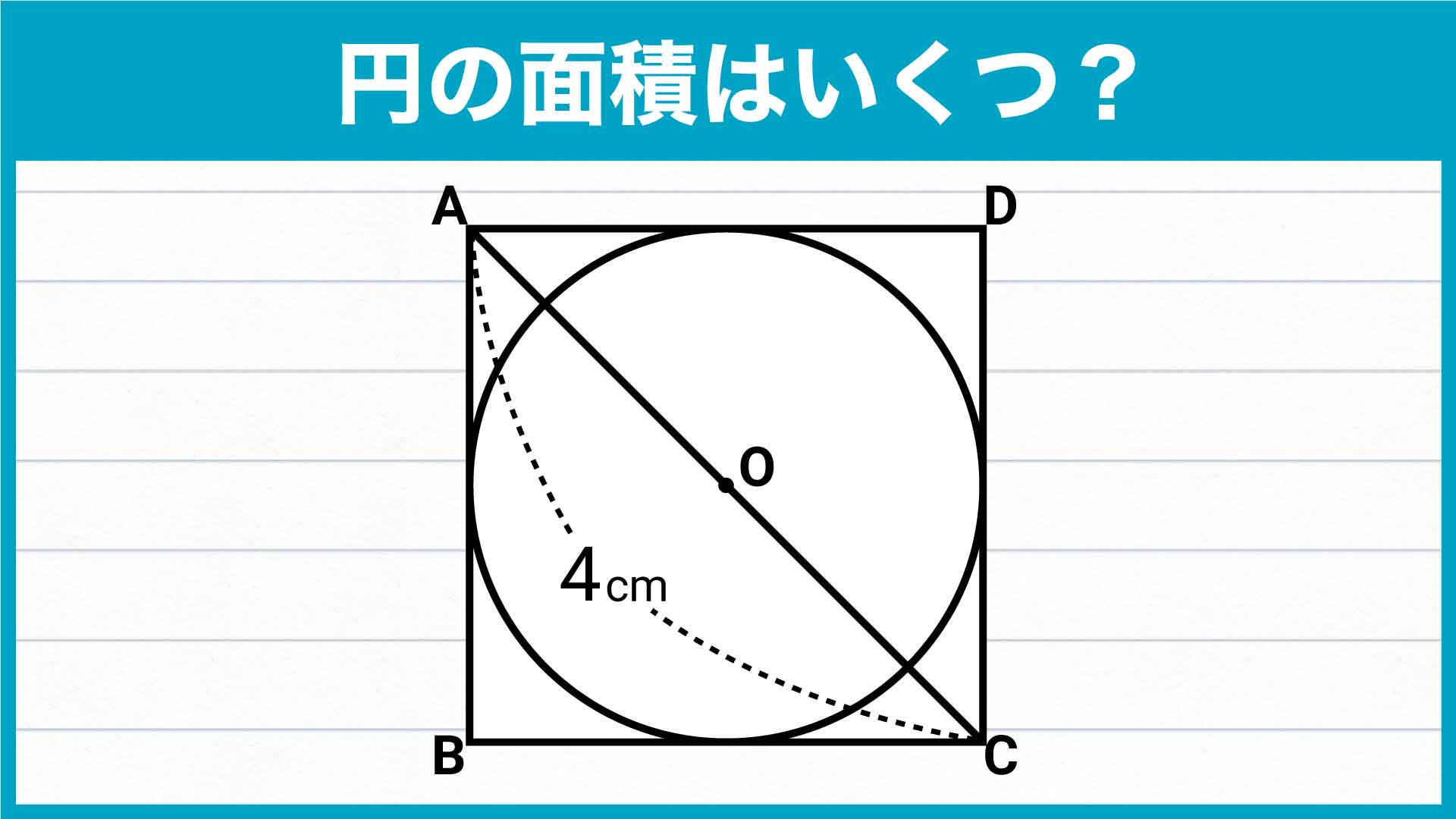
小学6年生の知識で解ける 円の面積 の問題 あなたは解けますか
円と放物線に囲まれた面積 微分法と積分法 おおぞらラボ
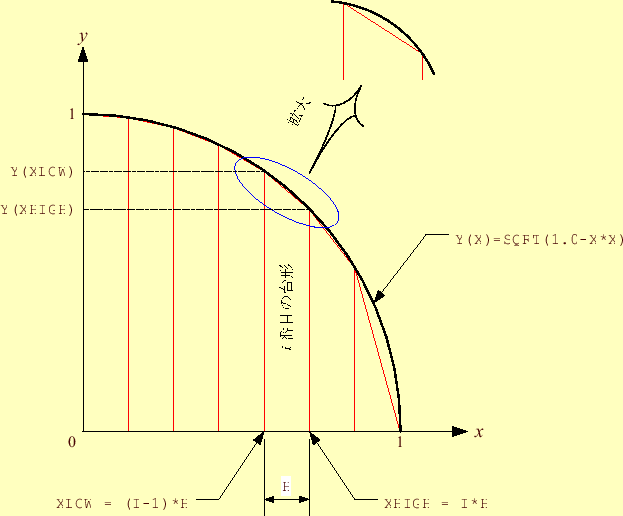
3 円の面積 数値積分の台形公式

円の面積 01 円の面積の公式 Youtube

円の面積比べ スクールプレゼンター教材共有サイト スクプレ道場

なんでこれ2分の1かけるんですか 円の面積って半径かける半径かけるpかける Clearnote
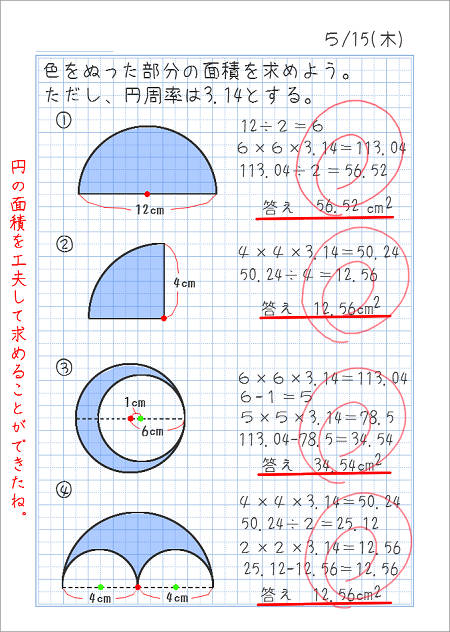
円の面積 その1 家庭学習レシピ
数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora
1
3
円の面積 置換法の意味 Geogebra
面積を求める

円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト
小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
円の面積 2 5

高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット

数学と物理学 面積分

数値積分による円の面積の計算 Java プログラミング 入門
円の面積

球の体積 球の表面積の公式の導出 積分 優技録

円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo

円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト

円の面積 球の体積公式の証明 理系ノート

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ
円 の面積 計算ドリル 問題集 数学fun
円の面積 その2 家庭学習レシピ
円の面積を求めたい エクセルの関数らくだ
積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典

山と数学 そして英語 小学校算数 円の面積に関する応用問題

解答 解説 便利なやり方 算数プリント6年生 円の面積 解説
勉強しよう数学 球の表面積を積分で求める

極方程式の面積 扇形積分 おいしい数学
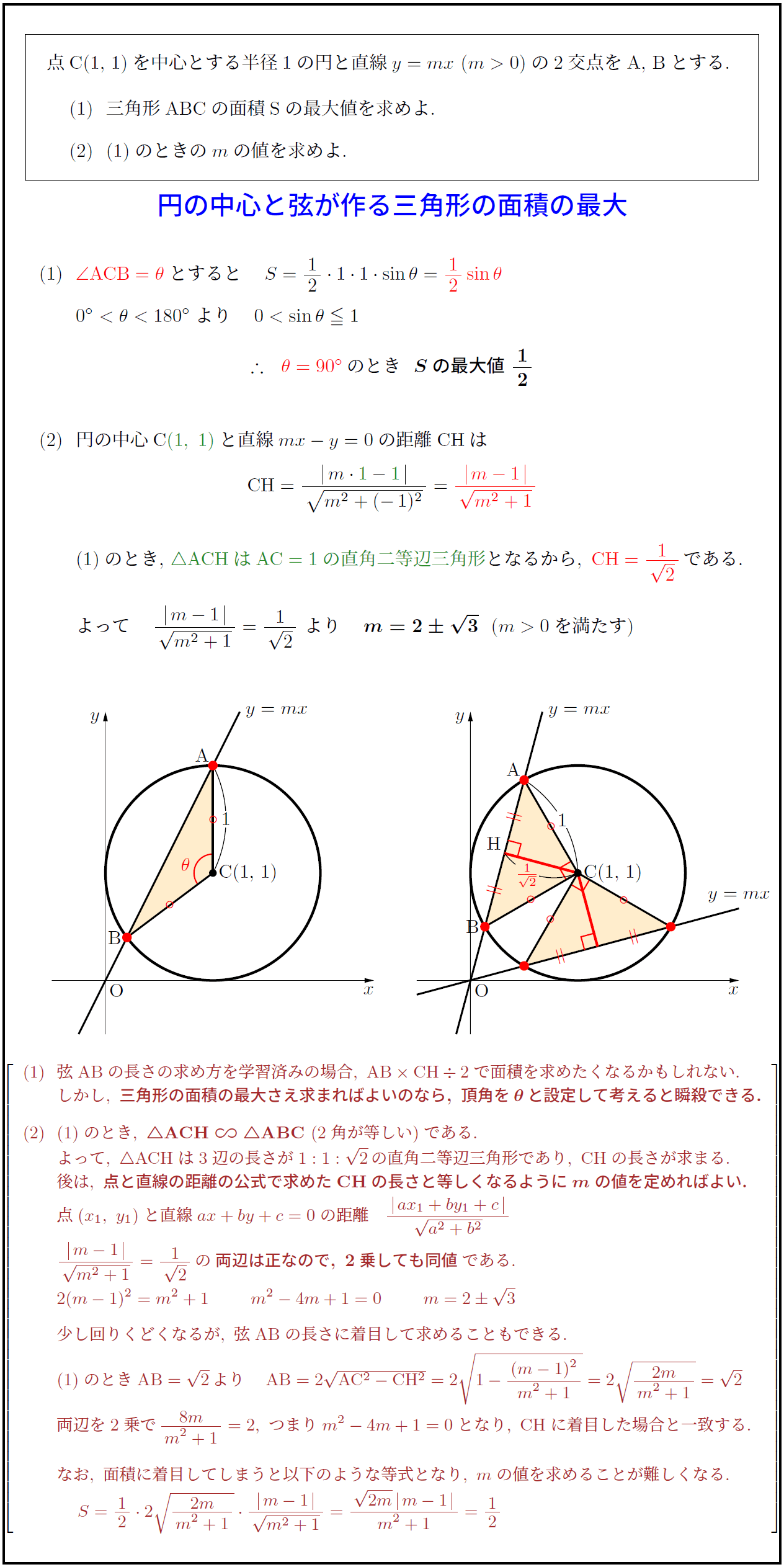
高校数学 円の中心と弦が作る三角形の面積の最大 受験の月

円の面積 練習応用 Youtube
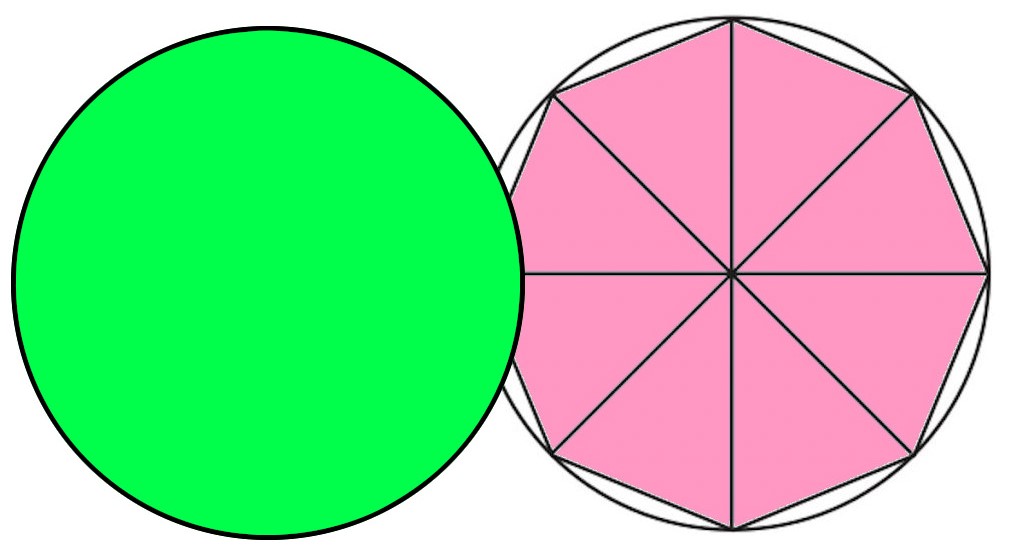
小6算数 円の面積 指導アイデア みんなの教育技術

円の面積 算数用語集
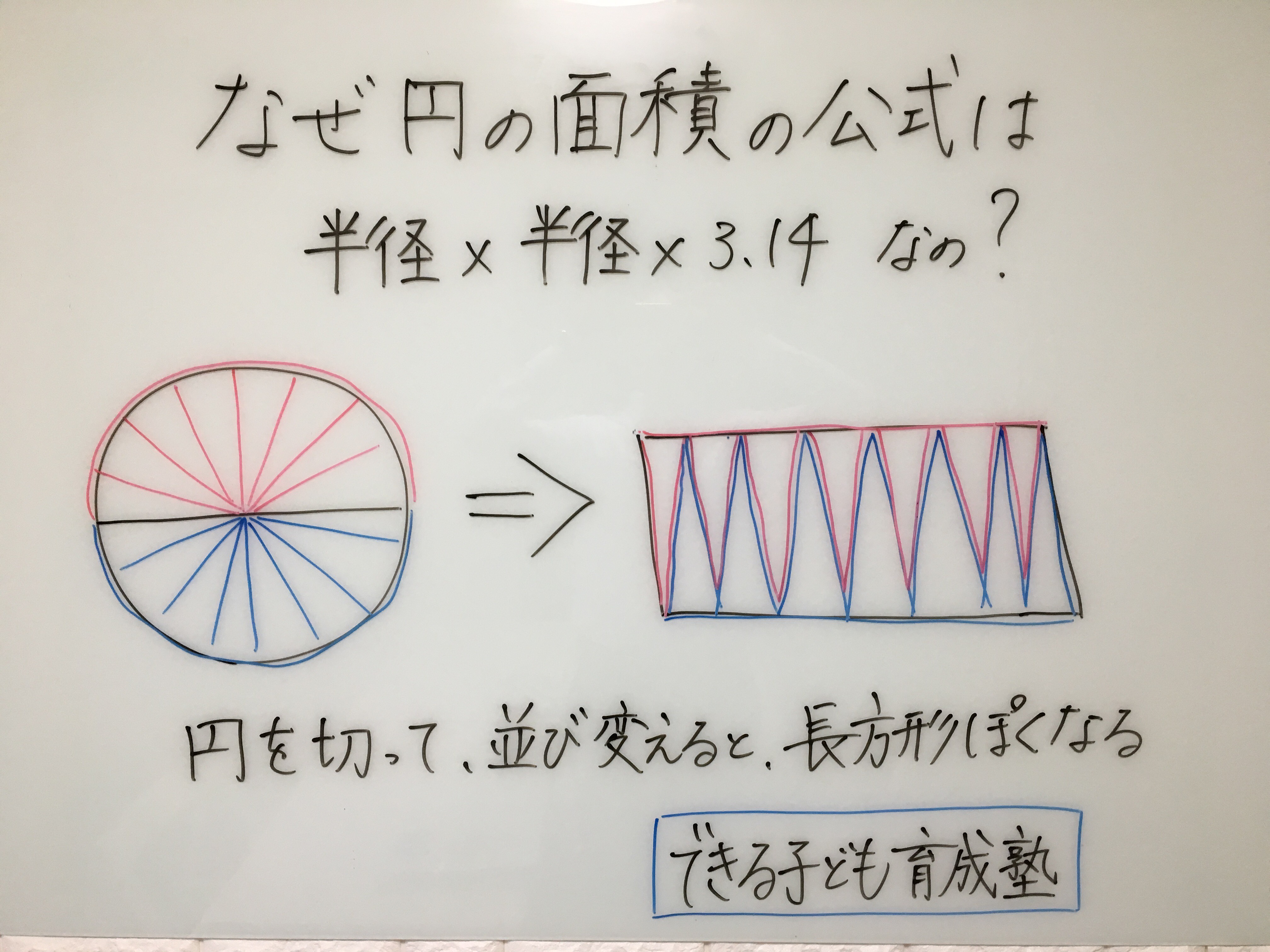
円の面積の求め方 公式 の理由を小学生に教える方法 元小学校教師が教える できる子ども育成塾 小岩 個別指導塾 小学生専門 国語と算数の苦手を克服
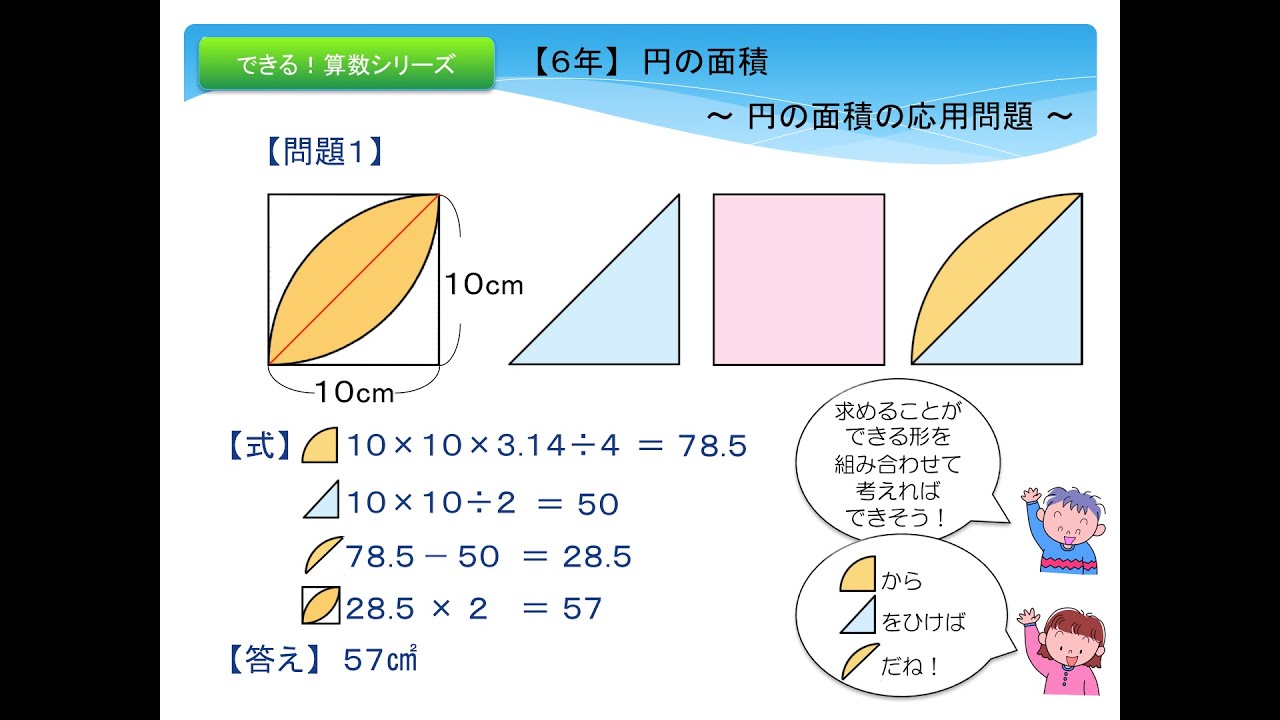
スマホok 6年 円の面積 円の面積の応用問題 Youtube
色のついた部分の面積の求め方 小学生
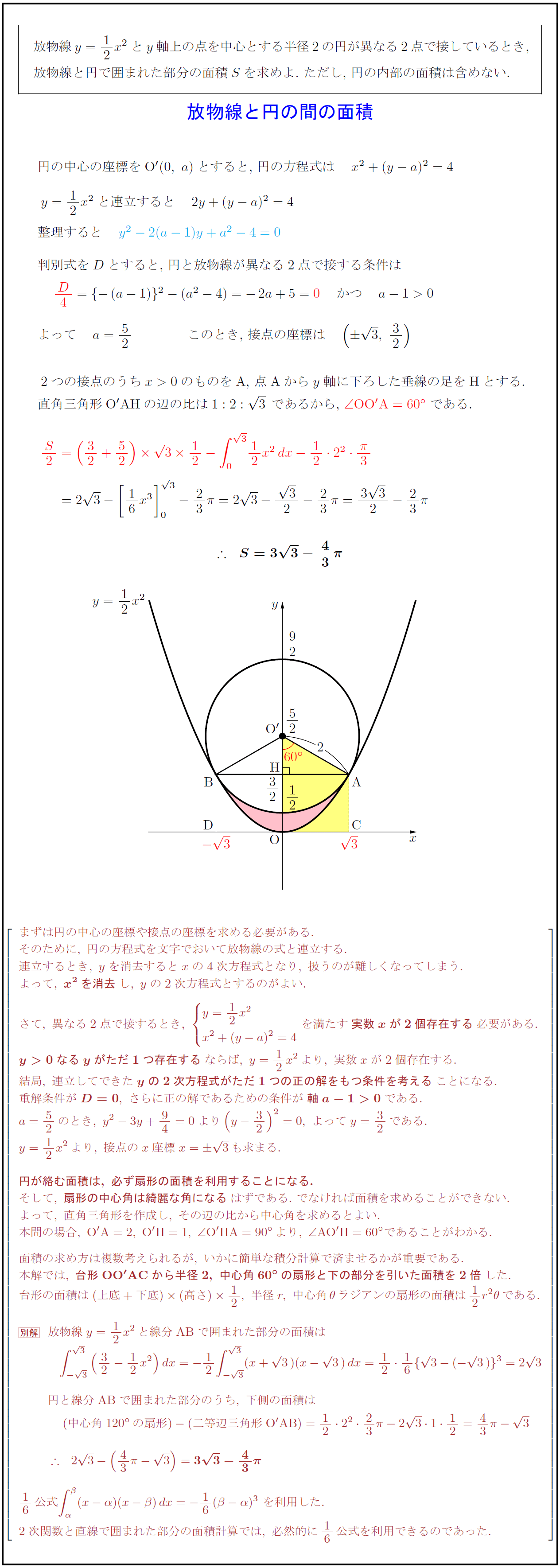
高校数学 放物線と円の間の面積 受験の月
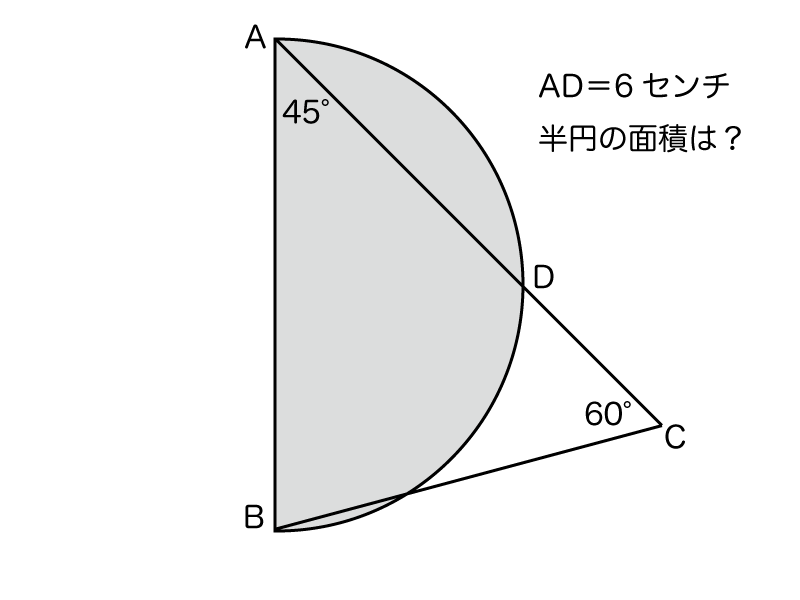
面積公式を組み合わせて解く半円の面積計算 受験算数入門
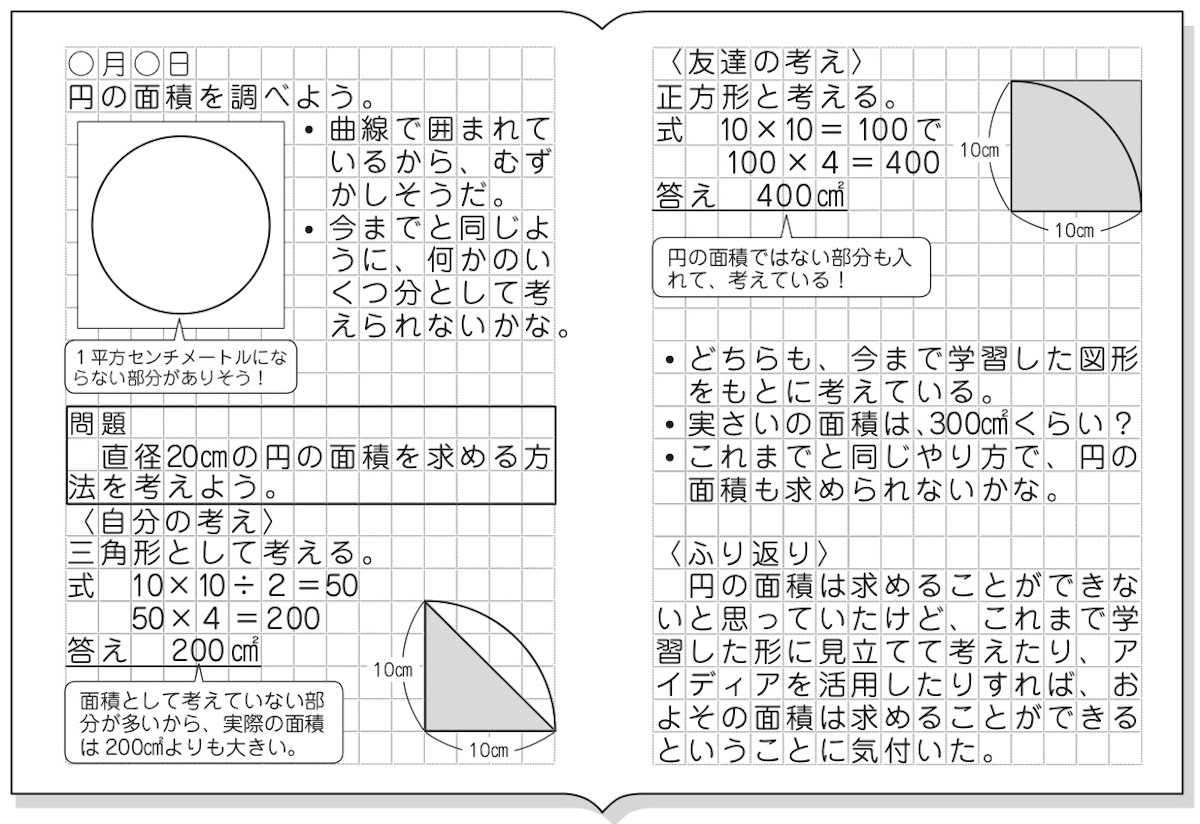
小6算数 円の面積 指導アイデア みんなの教育技術
この積分が半円の面積を示しているのは何故でしょうか Yahoo 知恵袋
積分
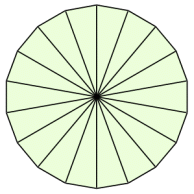
積分 円の面積の再考 大人が学び直す数学

円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




