三角形 角度 求め方 三角関数
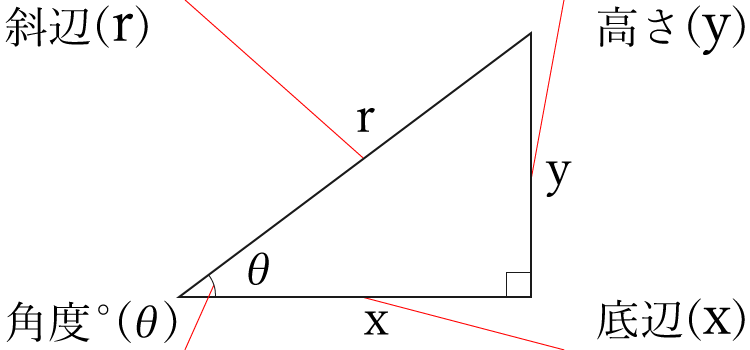
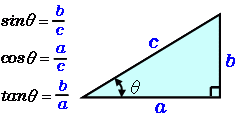
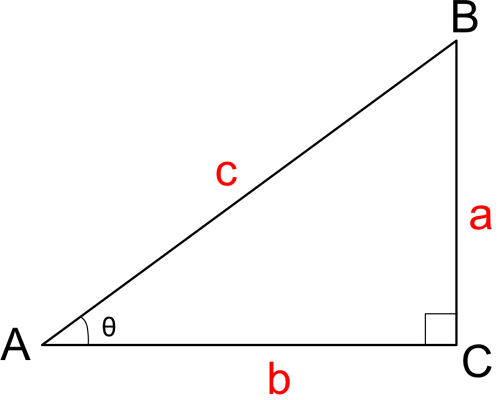
底辺と高さから角度と斜辺を計算 高精度計算サイト 底辺と高さから角度と斜辺を計算 ホーム / 数学公式集 / 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お.

三角形 角度 求め方 三角関数. 与えられている数値を確認する 三辺の長さ、または一つの角とその角を挟む二辺の長さが分かれば三角形の高さを求められます。 三角形の辺をa、b、c、角をA、B、Cとします。 三辺の長さが分かれば、ヘロンの公式と三角形の面積の公式を用いて高さを求めます。 二辺と挟まれる角が分かる場合は、A = 1/2ab (sin C)の公式を使って高さを求めます。 2 三辺の長さが分かればヘロンの公式を使う ヘロ. まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。. 三角形における三角比の値 ABCでcosB の値を求めよ。 という問題で,cosB =3/2 と答えてしまいました。 sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。.
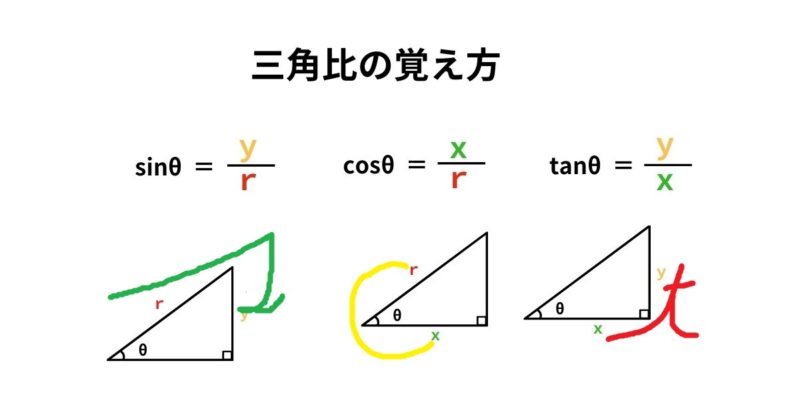
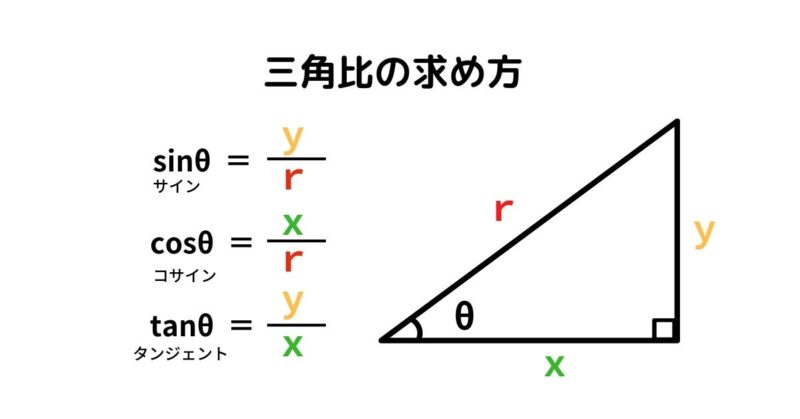
底辺と高さから角度と斜辺を計算 高精度計算サイト 底辺と高さから角度と斜辺を計算 ホーム / 数学公式集 / 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お. 三角関数の定義 sinθ = y r cosθ = x r tanθ = y x sin θ = y r cos θ = x r tan θ = y x ただし、 x = 0 x = 0 となるような θ θ に対して、 tanθ tan θ は定義されない。 弧度法(ラジアン)について 三角関数に用いる角度は、一般に ラジアン を用います。 ラジアンは次のように定義されます。 1 ラジアンは円の半径の長さに等しい弧に対する中心角の大きさ 1ラジアン このページで示している三角関数の公式. 三角関数の基本 まずは超基本の三角関数の公式から確認します。 原点 を中心とする半径 の円を描きます。 軸の正の方向(つまり右)に対して、線分 による角の大きさを とするとき、 三角関数の公式 , , このように表される三角比の関数のことを.
三角関数の定義 偏角を定義してしまえば, あとは三角比を$0^\circ\leqq\theta\leqq180^\circ$なる$\theta$にまで拡張したのと同じ考え方で,任意の実数$\theta$に対して$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を定義することができます. 三角比4|角度が90°以上の三角比はこう考える!. メタボが気になる方の健康計算、旧暦や九星のこよみ計算、日曜大工で活用される斜辺や面積の計算、高度な実務や研究で活きる高精度な特殊関数や統計関数など多彩なコンテンツがあります。 三角関数(度) 三角形の3辺から角度を計算 三角形の3. 最新 円 三角形 角度 問題 下の図のような三角形に内接する円の半径を求めなさい。 解答 超有名問題です。 \(2\) つの解き方を示します。 必ずどちらも理解・暗記しておきましょう。 解法1 円と接線の性質 円の中心と接点を結ぶ線分(半径)は小学生.
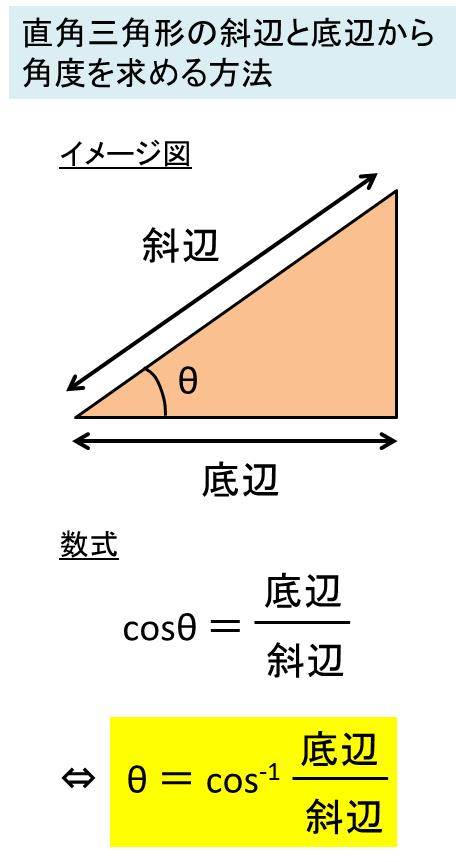
なお、斜辺と高さから直角三角形の角度を求めていくには、三角関数であるsin(サイン)の逆関数sin1を使用します。 上述の三角形において、sinθ=高さ/斜辺という関係式があるため、θ=sin1(高さ/斜辺)で角度を求めることができるのです。 エクセルでは、ASIN関数というものを使用していきます。 ASIN関数でもラジアン表記であるため、度数法での記載に変更していきましょう。 斜辺と高. 高知工科大学基礎数学シリーズ3 「三角関数」(改訂版) −11 − < 正弦定理1 > 三角形abc で,頂点a, b, c に対する辺の長さ を,それぞれ,a, b, c とする。また∠a, ∠b, ∠c の 大きさを,それぞれa, b, c と書くことにする。 このとき次の定理が成立する。. つまり、下の図のような直角三角形を考えたとき、sinθの2乗とcosθの2乗を足すと1になるということです。 ※三角関数では、sinθの2乗は「sinθ2」と書かずに「sin2θ」と書きます。 cos・tanでも同様です。 では、先ほどから使っている∠B=30°の直角三角形で.
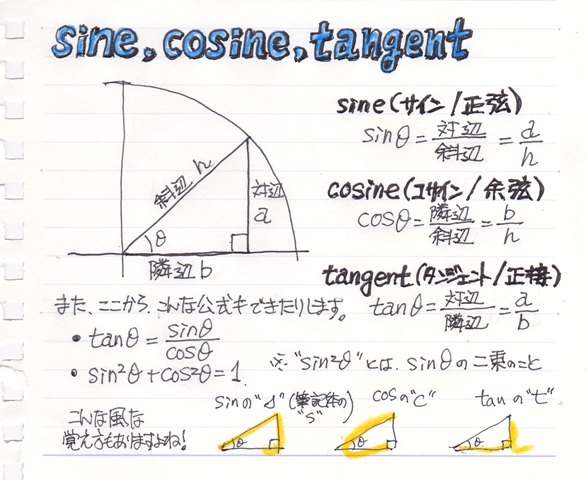
θ = y x で表される3つの三角比の関数のことを、 三角関数 と言います。 「 sin θ, cos θ, tan θ の分母・分子をド忘れしそう」と感じる方も多いかもしれませんが、これらはその 頭文字 s,c,t の筆記体 のイメージと結びつけると覚えやすくなり. 底辺5cm、高さ3cm、角度Θの三角形があったとし、 tanΘの求め方が tanΘ=3/5=06となり、 角度Θ=atan(06)=30°となるというのはわかったのですが、 atan(06)からどうして30°という数字が導き出されるのかがわかりません。. 三角形の求め方をしっかり覚えて、スムーズに求められるまで繰り返し学習しましょう。 では、以下に重要なポイントをまとめて終わります。 \(30^{\circ}, 45^{\circ}, 60^{\circ}\)の三角比は三角形の辺の長さをしっかり覚えると求めることができる.
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま. 三角比では0°から180°の角を、そして「三角関数」では180°より大きい角などに広がっていく。 この方法で値を見つけていくと、下記の表の値をすべて埋められるようになる。 以下では、参考までに0°から180°までの有名角と、その三角比の値を示す。 30°、45°、60°の三角比の値と同様に、これらの値を、丸暗記ではなく「なぜそうなるのか」を考え、値をいつでも出せるように. 基本的に、三角関数の角度は 半径 の「単位円」 を利用して求めることができます。 単位円 周分の角度は、度数なら 、ラジアンなら です。 度数とラジアン、どちらの角度で聞かれても問題なく書けるようにしておきましょう。 補足 「度数とラジアンの変換」については、以下の記事で詳しく解説しています。 ラジアンとは? 弧度法とは? 定義や角度変換をわかりやすく解説 単位円.
52°の三角形の辺の比はわかりませんが,sin 52°,cos 52° の値なら計算機に打ち込めばすぐ求められます。 もちろん52°というのは1つの例であって,他のどんな角度でも sin,cosを斜め方向の力に かけ算することで分力を求めることが可能 です。. 角度 θ = tan − 1 ( h a) 面積 S = 1 2 a h EXCELの数式. あとは、直角三角形の角度と辺の比の関係から、三角比の値を求めていきます。 解答 答え: 、、 計算問題②「cos θ = 1/2 を満たす θ を求める」 計算問題② のとき、 を満たす をすべて求めよ。 は動径の 座標の値でしたね。 また、求める の範囲と単位 にも気をつけましょう。 今回は なので、範囲は単位円 周分、単位はラジアンを考えます。 解答 単位円周上で 座標が となる点は、図の点 、点 であ.
三角関数の角度は「三角関数の逆関数」を求めることで算定できます。 三角関数y=sinθについて、θ=の形になるような関数を「アークサイン(Arcsin)」といいます。 例えばsin (π/2)=1のとき、逆関数をとるとArcsin (1)=π/2≒157(≒90°)となります。 よって「sinθ=035」のようにθが未知数の場合、アークサインをとることでθを逆算できます。 今回は三角関数の角度の求め方、公式と計算、表. 1 三角関数の定義 動径 が 軸の正の向きをなす角度を とするとき,次の比の値は(相似図形の性質から)半径 の大きさに関係なく,角度 だけで定まる.そこで, の関数になり,三角関数と呼ばれる. 2 三角関数の性質 ※以下においては,角 として第1. 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求められます。 たとえば、「底辺 9 c m 高さ 6 c m の三角形」の面積は 9 × 6 ÷ 2 = 27 c m 2 となります。 なぜ 底辺 高さ 底 辺 × 高 さ ÷ 2 で求まるのかについては 「三角形の面積の求め方。 なぜ底辺×高さ÷2で求まるのか? 」 で解説しています。 ② 直角三角形・正三角形の性質を使って求める 「底辺 a 、斜辺 c の直角三角.
三角関数の角度を求めるときは、θの範囲を忘れないこと それぞれの求め方をまとめると 単位円 を書いて、三角関数に適した直線を書き込み交点を求める。 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるか 確認する という手順で三角関数の角度を求めることになります。 慣れてくればこの手順を意識しなくても自然と角度を求められるよう. ACOS関数の計算式の形 『=ACOS(数値)』 三角形の辺の比から角度を計算する関数 数値は、『1~1』の間の値になる。 それ以外の数値はエラーになる 計算結果の角度はラジアンの表記で出て来る 度数法で表示する際には、『DEGREES関数』を使用する COS(コサイン)関数と言うのもありますが、COS関数の場合は、角度から辺の比を求められます。 COS60°であれば、1/2(2分の1)でした. 三角関数 三角関数でまずしっかりおさえておきたいのは、やはり sin \sin sin (サイン)、 cos \cos cos (コサイン)、 tan \tan tan (タンジェント) です。 サインとコサインとは何かを覚えるときに、直角三角形の辺の関係だけで覚えていると応用し.
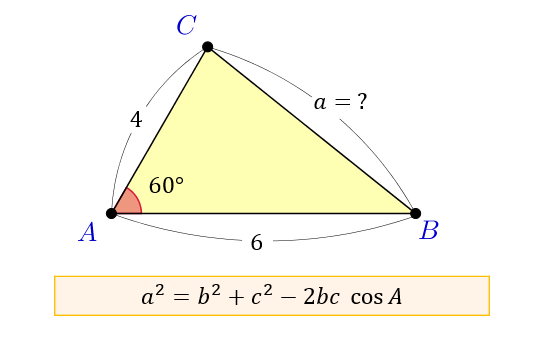
角度30度の三角形は、1対2対ルート3なので、 y座標は、長さ2の半分の『10』です。 x座標は、10のルート3の為、『173』で合ってますね。 この計算は、円を描く時など、イロイロな場面で出てくると. 三角形の2辺と一つの角度から他の角の大きさを求める これは、「パターン1:三角形の3辺の長さから角度を求める」の応用で求めることができます。 まず、余弦定理を使って、長さが不明である辺の長さを求めます。 すると、3辺の長さがわかるので、残りの角度も計算できます。 タグ 三角関数 「 カプレカ数6174から6桁のカプレカ数まで考えた 」 「 カードを使った条件付き確率. サイン・コサイン・タンジェントの覚え方は「三角関数の基礎知識。 参考にしてみてください。 正弦定理 正弦定理とは何か?2つの視点から分かる公式の覚え方・考え方 三角形 \(abc\) に対して、点 \(a,b,c\) 四角形の面積の求め方まとめ。.
三角形の3辺から角度を計算 水平線までの距離を出すプログラムを作るのに参考にした。 わかりやすくて便利ですね。 台形型の部屋の変形のコーナーに壁にピッタリと合った棚を作ろうと思い図面を牽きましたが角度の算出方法が分からずお世話になり. ・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。. 角度を入力し「角度から三角関数を計算」ボタンをクリックすると、入力された角度から三角関数を計算し表示します。 三角関数は、サイン(正弦) sinθ、コサイン(余弦) cosθ、タンジェント(正接) tanθ、コセカント(余割) cscθ、セカント(正割) secθ.
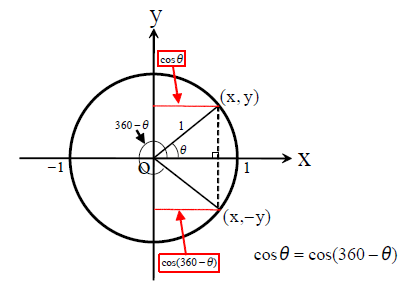
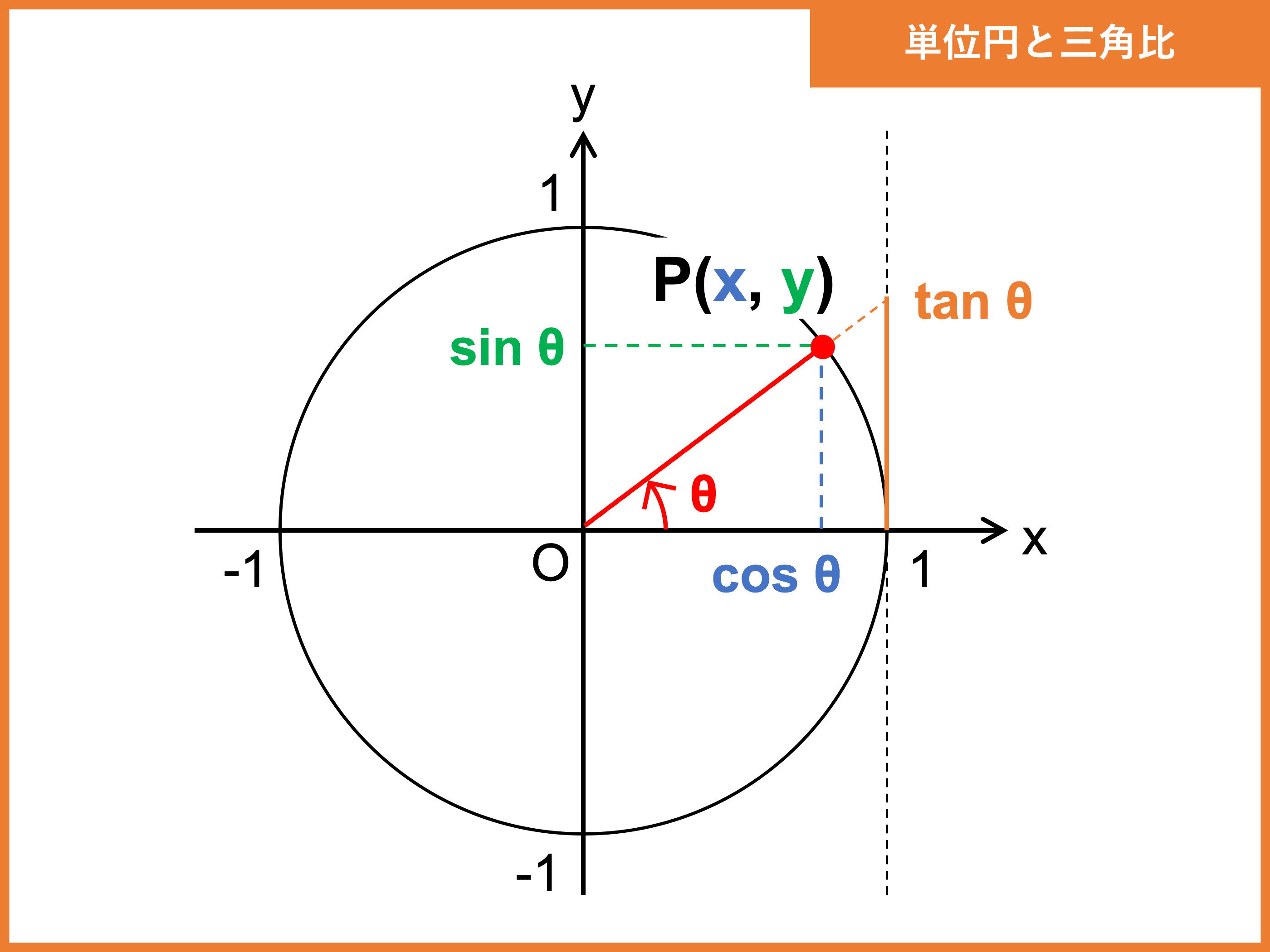
三角関数の定義のポイントは、 cos、sinは円のX座標、Y座標であるということです。 x軸の正の向きからθの角度をつけた直線を書くと円と交わりますよね。 この時のx,y座標がcosθ,sinθなのです。 半径1の単位円上の座標ということを考えると という範囲の. 全て直角三角形の辺の長さの比 を表しています。 三角形は辺が3本ありますよね。 仮に辺をA, B, Cとすると、 $$①AB\\②BC\\③CA$$の3つの比が出来ます。 この\(①②③\)がそれぞれ\(\sin, \cos, \tan \)になるイメージです。 もう少し詳しく、1つずつ解説していき. こんにちは。 da Vinch (@mathsouko_vinch)です。 三角関数においてある角度の三角比を「覚える」のはナンセンスです。なぜなら三角関数では角度はいくらでも大きく、またマイナスの角度も考えられますから。さらに私たちがち.

三角形の辺から角度を計算 製品設計知識
工業用 三角関数計算ツール

三角関数で角度から座標を導くふたつの式の使い途 Qiita
三角形 角度 求め方 三角関数 のギャラリー
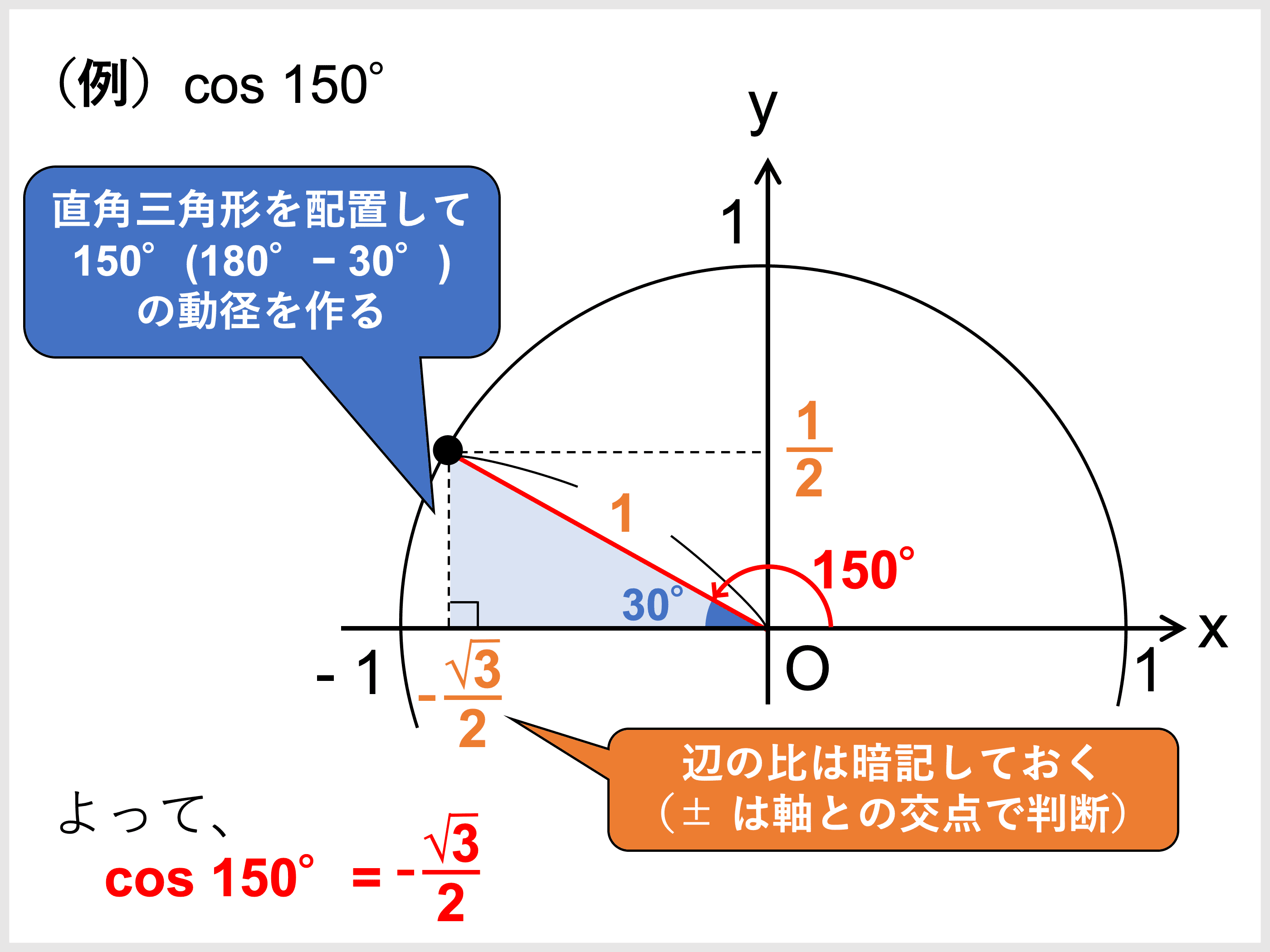
三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
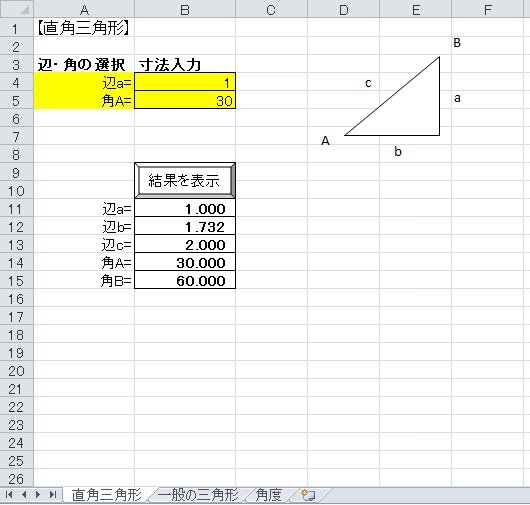
エクセル 三角関数計算 S Project

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
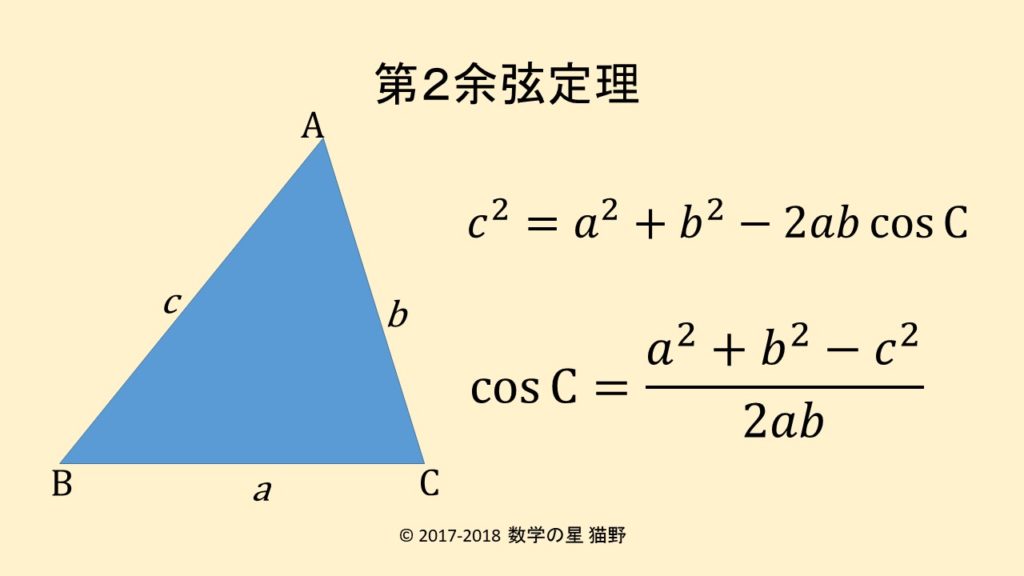
第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
三角関数 度 高精度計算サイト
三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
直角三角形の斜辺の長さと角度が分かっている場合 他の2辺の長さを求めたいので Yahoo 知恵袋

中級16 Sin Cos Tan関数
余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
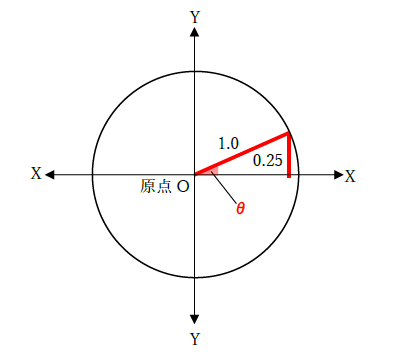
三角関数の角度は 3分でわかる求め方 公式と計算 表との関係

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

黄金三角形による18 シリーズの三角比 おいしい数学

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
1

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三角関数の基礎知識

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
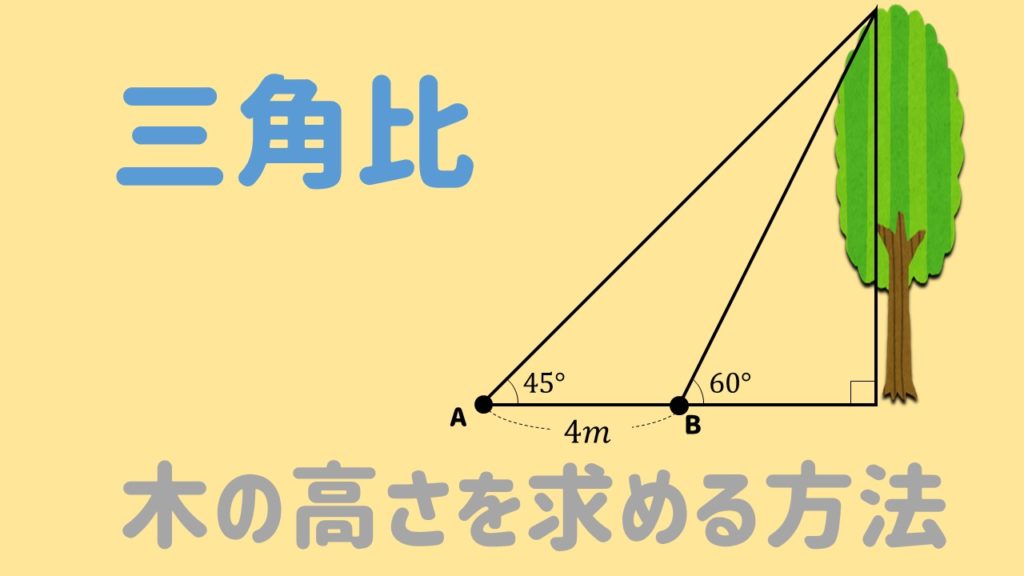
高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

小5 算数 小5 31 三角形の角 Youtube
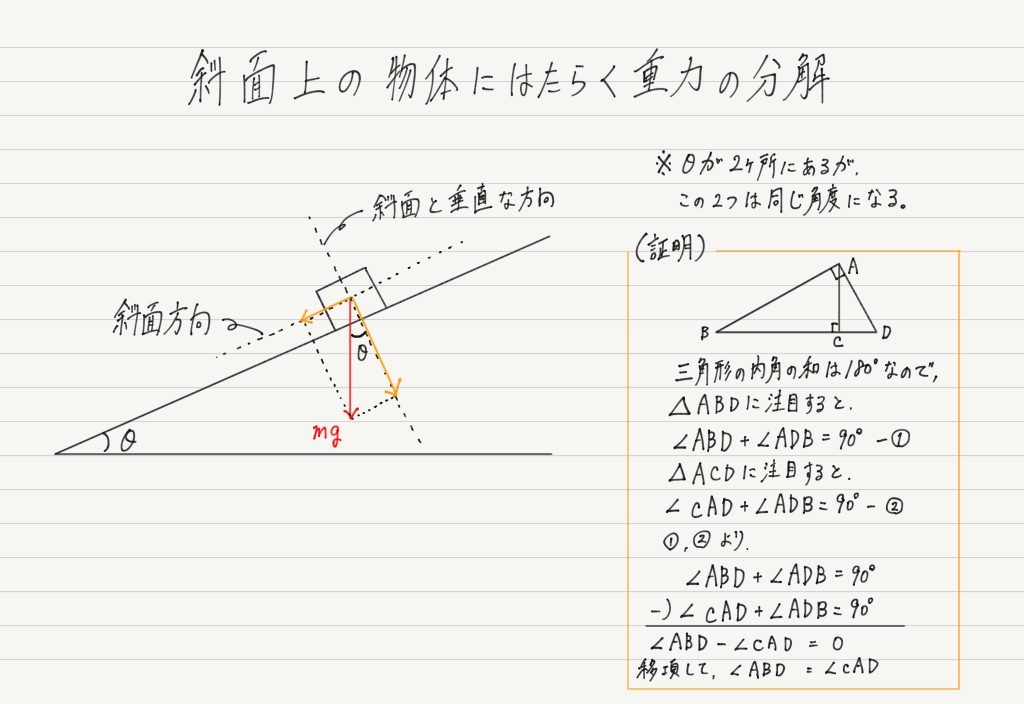
力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に
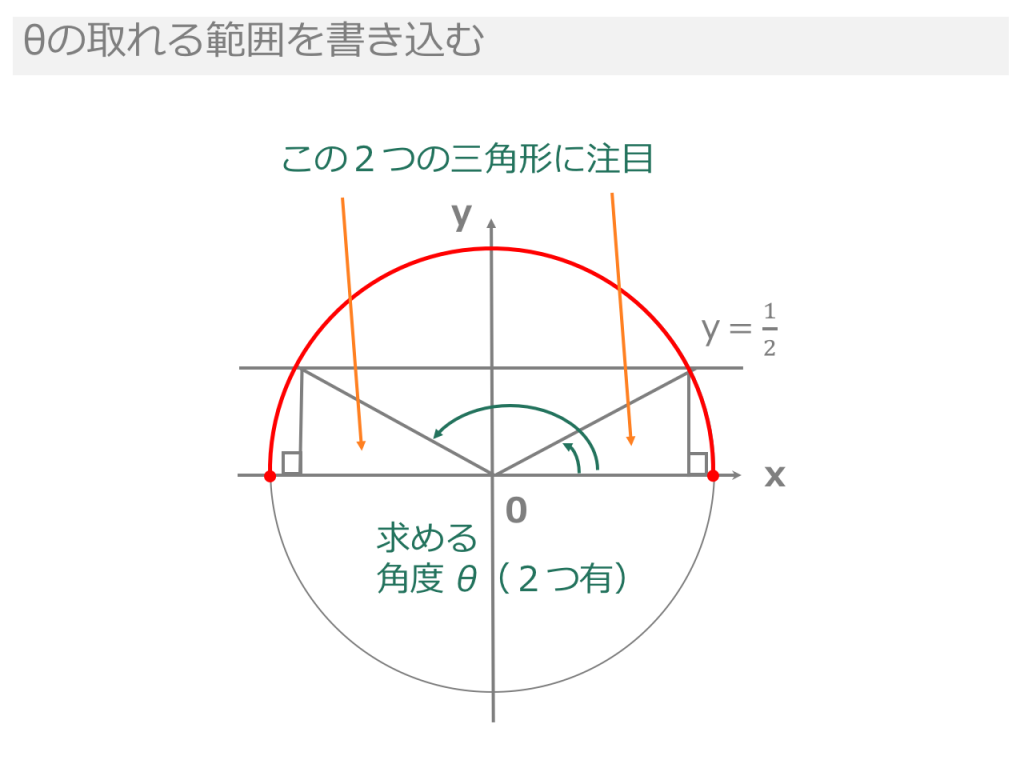
3分で分かる 三角方程式の解き方 単位円を用いた三角関数の角度の求め方 をわかりやすく 合格サプリ

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
3

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
三角関数で直角三角形の辺の比率を求めてみた サイン コサイン タンジェントとか Excel 三角関数 Haku1569 Excel でらくらく データ分析

サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
数学関数 逆三角関数 Acos ゆるゆるプログラミング
数i 基本的な三角比の値

簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

高校数学 数 76 三角比 基本編 Youtube

高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット
直角三角形の解法 1

タンジェントとは何か 中学生でも分かる三角関数の基礎

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要
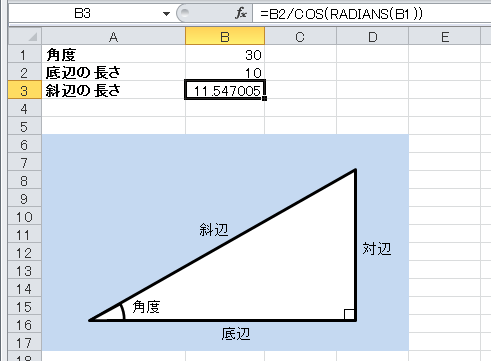
角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス

有名角 準有名角のsin Cosの値 一覧 理系のための備忘録
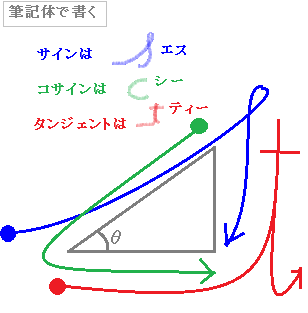
数i 基本的な三角比の値
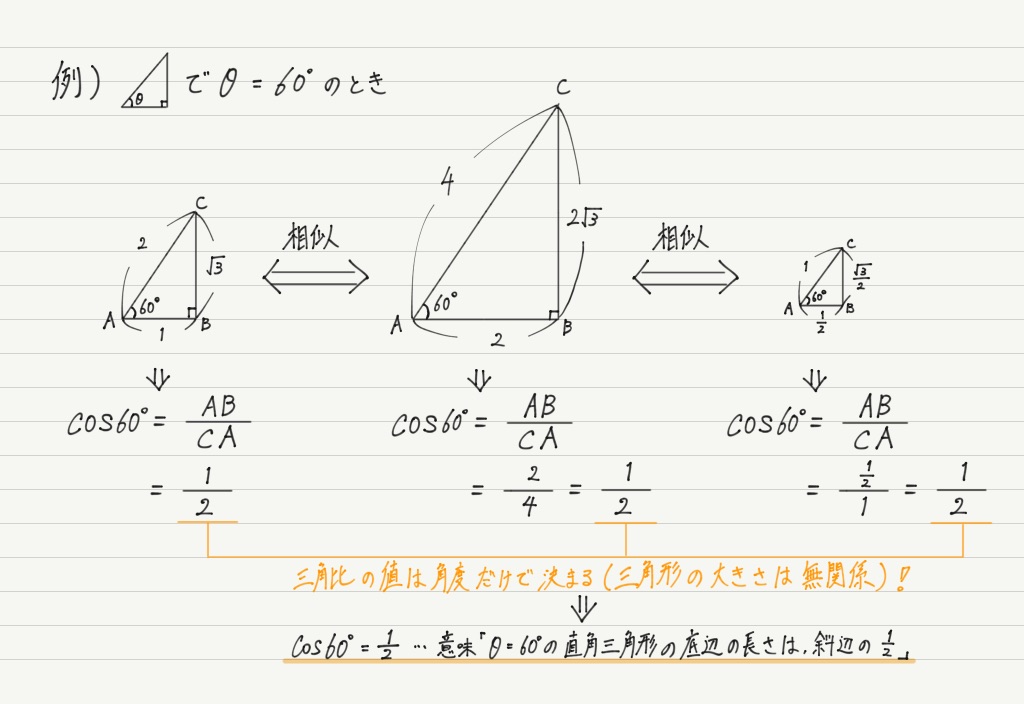
三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
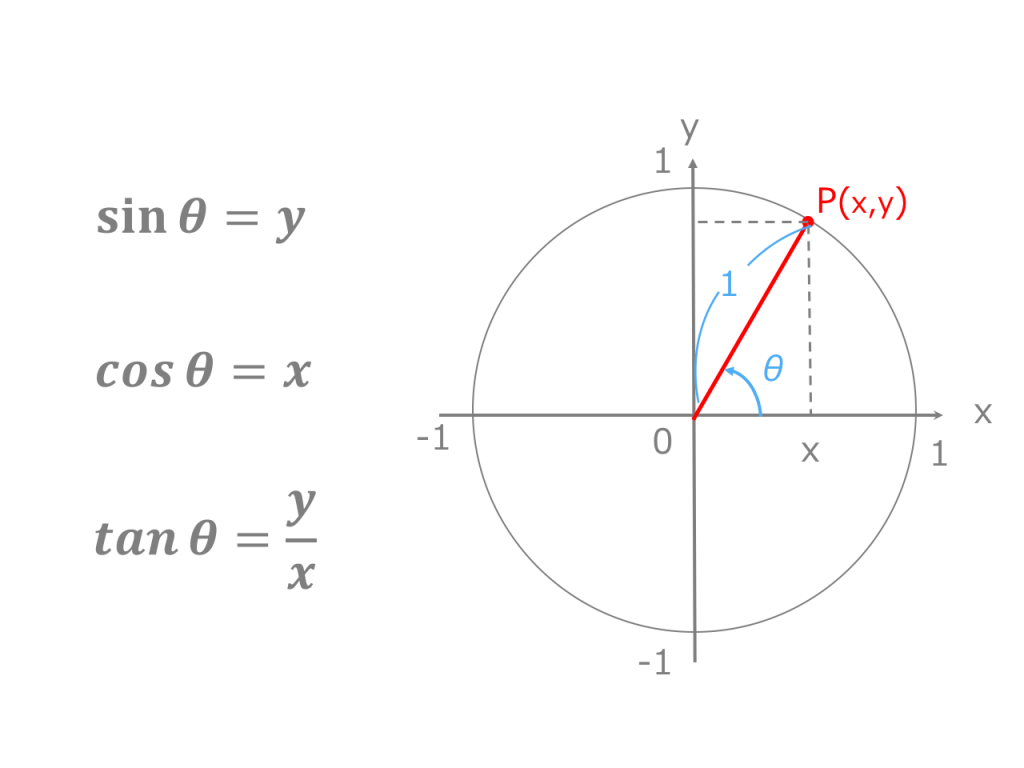
3分で分かる 三角方程式の解き方 単位円を用いた三角関数の角度の求め方 をわかりやすく 合格サプリ

余弦定理で角度を求める方法 数学の星

三角形の角度を求める 思考力を鍛える数学

タンジェントとは何か 中学生でも分かる三角関数の基礎

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi
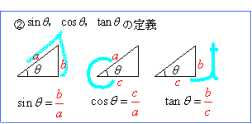
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

角度の求め方 算数の教え上手 学びの場 Com
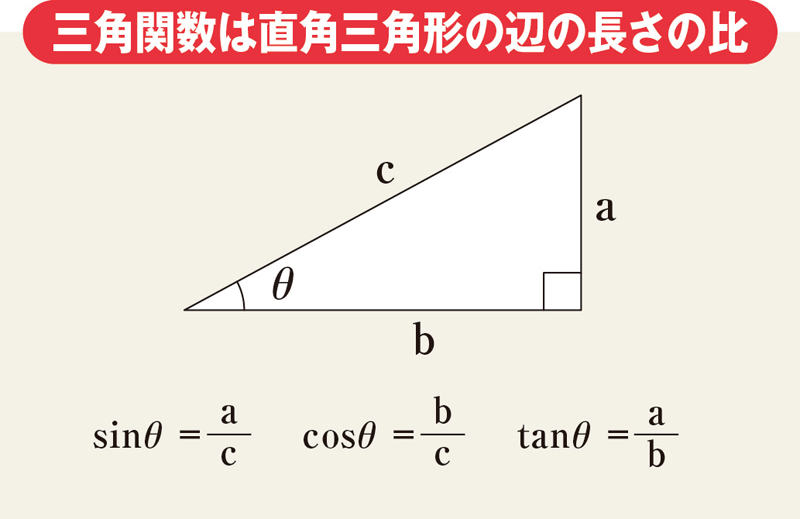
家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン
直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
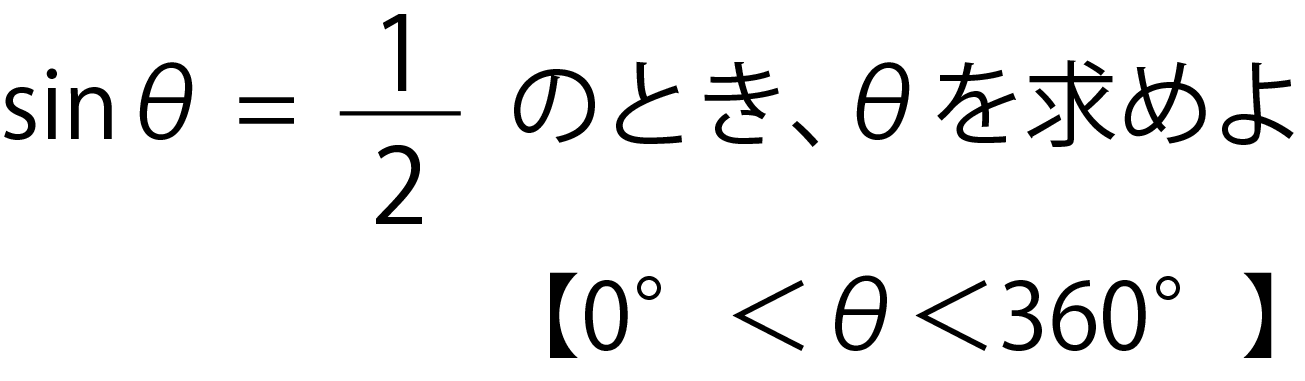
三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
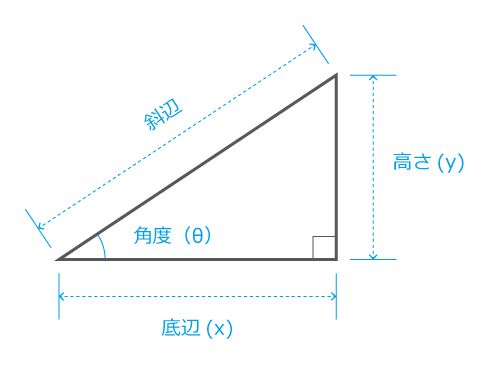
Windows電卓で三角関数を計算する方法 Trismegistuslabo トリメギブログ
Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

三角形の3辺から角度を計算 高精度計算サイト
三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo

いただいた質問に答えてみる 関数表にない三角関数の求め方 編 中山祐介の土地家屋調査士 測量士補 合格 ブログ
三角関数から角度 逆三角関数 三角形の計算 計算サイト

有名角の三角関数は覚えるな 図から簡単に判断するコツ
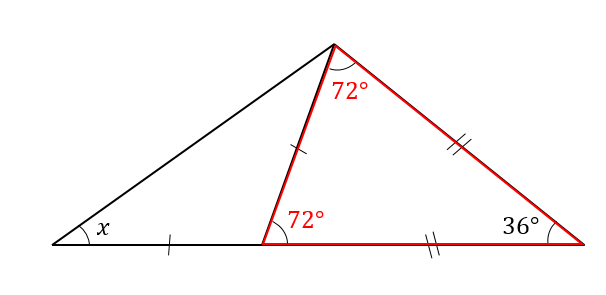
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
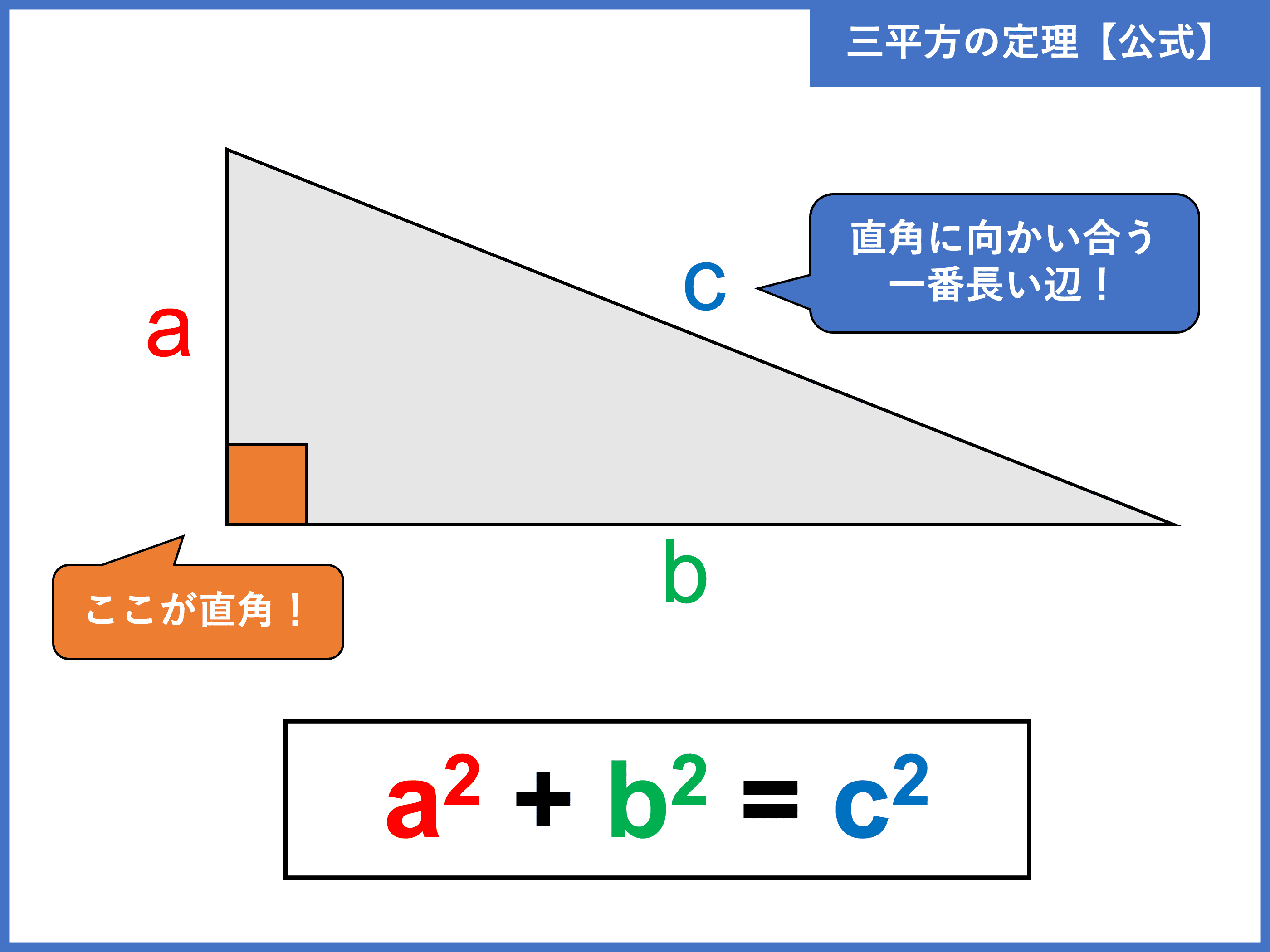
三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
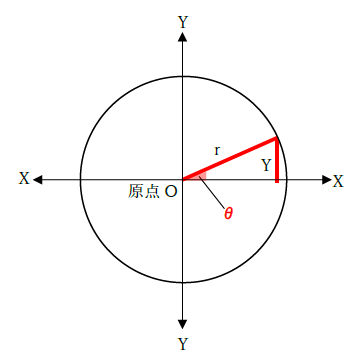
三角関数とは 1分でわかる意味 公式と計算 角度と値の関係

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

P Class Text 13 三角形 内心 角度 求め方
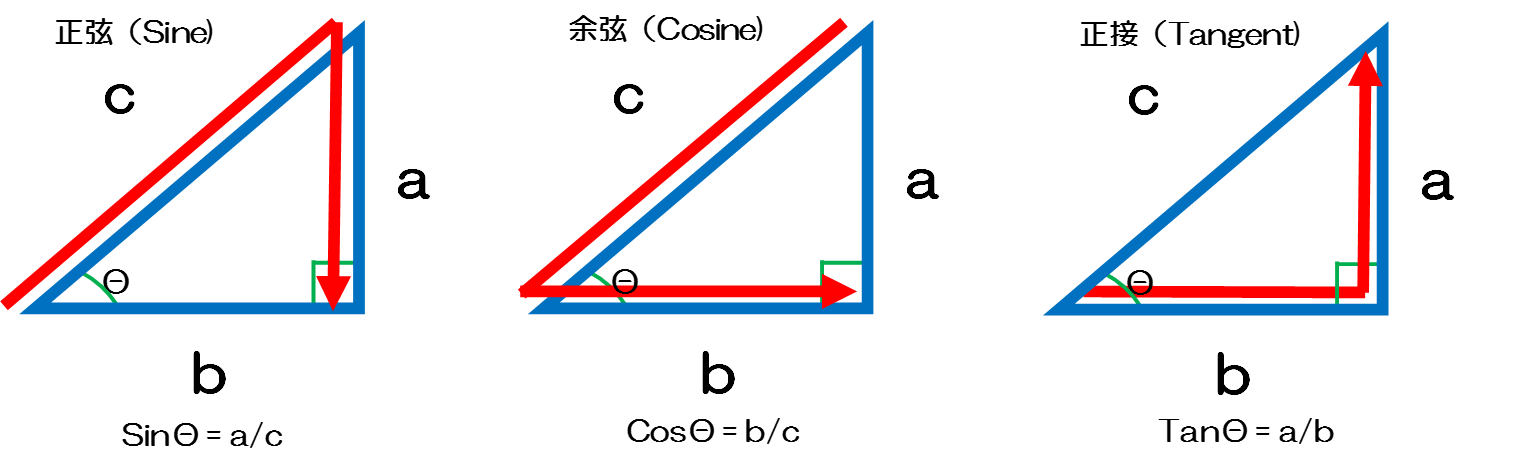
Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数
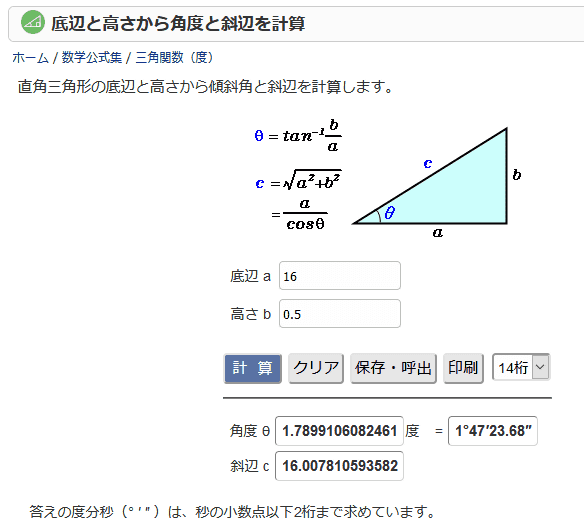
表計算ソフトを使って 底辺 と 高さ から 角度 を求める

わかりやすい三角比と基本公式 Irohabook

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
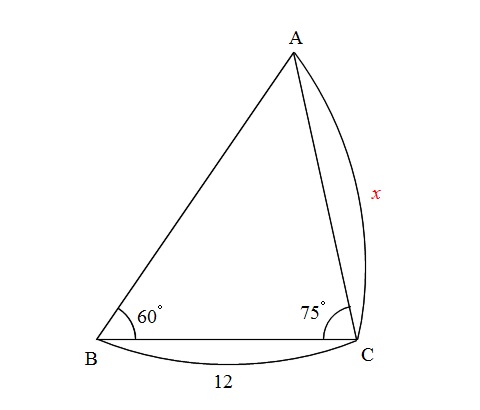
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
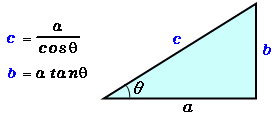
角度と底辺から斜辺と高さを計算 高精度計算サイト
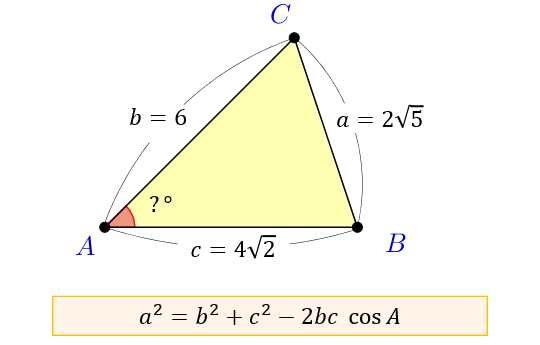
余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

三角関数の基礎知識

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
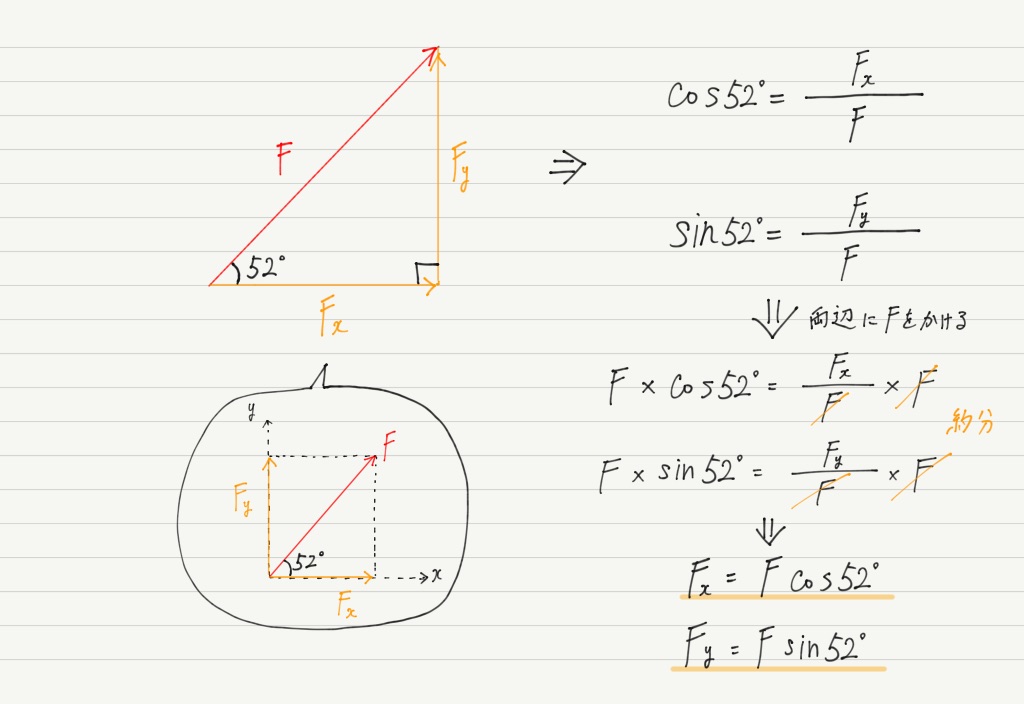
力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に
品質管理 Xyz
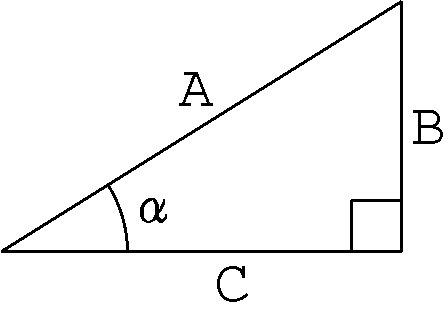
Sin Cos 1 Cg Mathematics Ad04

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
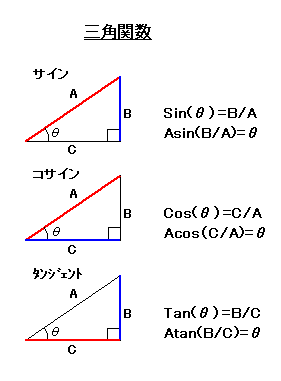
正確な角度の測定 割り付け

三角関数の定義 鈍角の三角比を工学博士が解説 完全に理解できます トムラボ
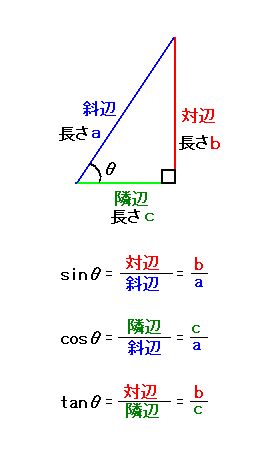
三角関数について
余弦定理 公式

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

三角比を考え方から理解する 有名角の三角比も説明

余弦定理を使った計算 3辺のみが与えられた場合 数学i By Okボーイ マナペディア

16 合成公式はsinだけじゃないんです 医学生gの数学ノート
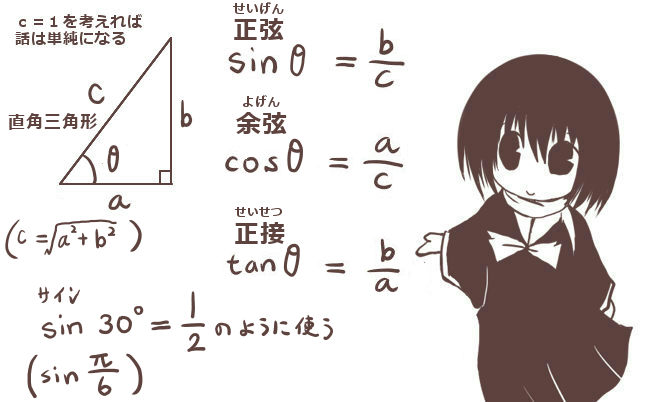
直角三角形の辺の比の関係 Sin Cos Tan 理数系無料オンライン学習 Kori
上級 三角関数 Shade3d チュートリアル
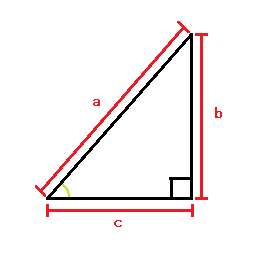
2点間の距離を測ろう 三角関数 Gameworks Lab

底辺と角度から 高さを求める ある高さの木から 10m離れて 木のてっ Okwave

三角形の面積公式まとめ 求め方をわかりやすく解説 受験辞典

直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage
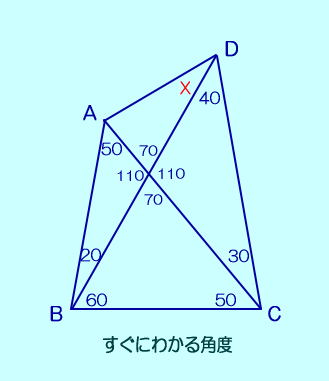
ラングレーの問題 整角四角形
1
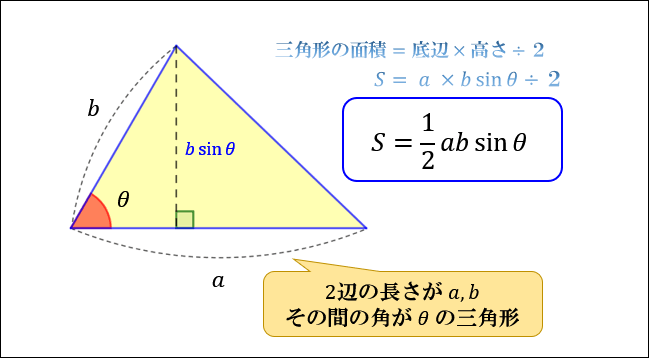
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

底辺と高さから角度と斜辺を計算 高精度計算サイト




