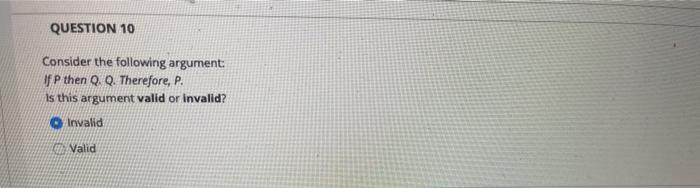
If P Then Q Q Therefore P
And if p then r;.

If p then q q therefore p. P then q” or “p implies q”, represented “p → q” is called a conditional proposition For instance “if John is from Chicago then John is from Illinois” The proposition p is called hypothesis or antecedent, and the proposition q is the conclusion or consequent Note that p → q is true always except when p is true and q is false. Mathematics, a variety of terminology is used to express p !. The channel that brings you the best shit shows in FE o7🤡 #feclownshow 🤡 Air Date.
And the conclusion is q then (p 1 ∧ p 2 ∧ ∧ p n) → q is a tautology •Inference rules are all argument simple argument forms that will be used to construct more complex argument forms Next, we will discover some useful inference rules!. How to think about P ⊃ Q in plain EnglishIn propositional logic, P ⊃ Q is what is called a material implicationIt doesn't mean that P and Q mean the same thing (they might not have the same truth value);. (See this post for an explanation of the conditional) Even if you have If ( P implies Q ) then ( P implies R ).
And if p then r;. An argument of this form—If p, then q;. If p, then q Not q Therefore, not p If you don’t care, fuck off The Rubber Duck method of debugging We called it the Rubber Duck method of debugging It goes like this 1) Beg, borrow, steal, buy, fabricate or otherwise obtain a rubber duck (bathtub variety) 2) Place rubber duck on desk and inform it you are just going to go over some.
Therefore if p is true then q and r are true De Morgan's Theorem (1) ¬. If p then q;. Q if p , then q q , ifp p , only if q p implies q p is sufcient for q q is necessary for p q follows from p c Xin He (University at Buffalo) CSE 191 Discrete Structures 15 / 37 Terminology for implication Example Proposition p.
Q is valid,that is always a TRUE implies a TRUE irrespective of the relations between the terms of the propositions P and Q in the russelian (material) definitionOn the other hand there is a necessary one between P. But either not q or not s;. Look at the fourth (or sixth) row In this case, \((P \imp R) \vee (Q \imp R)\) is true, but \((P \vee Q) \imp R\) is false Therefore the statements are not logically equivalent While we don't have logical equivalence, it is the case that whenever \((P \vee Q) \imp.
Therefore p is true Conjunction p,q ∴ (p∧q) p and q are true separately;. If p then q p Therefore, q If p then q Notq Therefore, notp Exposition The consequent of a conditional statement is the part that usually follows then The part that usually follows if is called the antecedent I write usually here because there are many different ways to make a conditional statement, but we needn't go into. Therefore, q If p, then q q Therefore, p * 9 The invalid argument form known as denying the antecedent has the following pattern_____ Within arguments of this form, it is possible for the conclusion to be false while the premises are true, which makes the form invalid See Page 86 If p, then q Not p Therefore, not q If p, then q p Therefore, q If p, then q q Therefore, p If p,.
Therefore they are true conjointly Addition p ∴ (p∨q) p is true;. P q p → q ∼ q ∼ p T T T F F T F F T F F T T F T → F F T T T In this case there is only one critical row to consider, and its truth value it true Hence this is a valid argument Result 22 (Generalization) Suppose p and q are statement forms Then the following arguments (called generalization) are valid p p∨q q p∨ q Result 23. If p then q Notp Therefore, notq If p then q p Therefore, q If p then q Notq Therefore, notp Example I want to list seventeen summary statements which, if true, provide abundant reason why the reader should reject evolution and accept special creation as his basic worldview.
Invalid argument forms Consider the following argument form p q Therefore r If we let p be 'It is raining in the southeast', let q be 'increased rain usually helps crops produce a higher crop yield' and r be 'crops in California will produce more' then the resulting argument is not valid (check to make sure you see a possible way to have all true premises and a false conclusion). (p ∧ q) ├. P → Q Q → RP → R 1 Disjunctive Syllogism (DS) Either Ralph walked the dog or he stayed home Ralph did not walk the dog Therefore, he stayed home ===== Either P or Q Not P Therefore, Q ===== P v Q ~PQ 1.
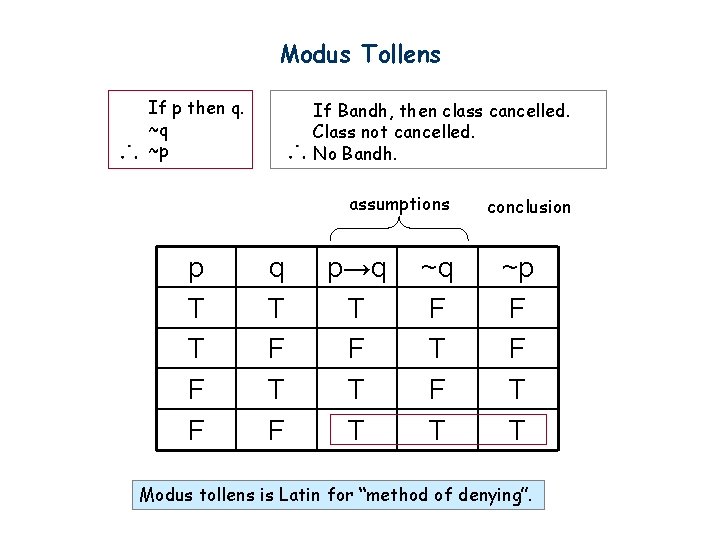
Therefore Q (You can negate the P or the Q interchangeably) False Dilemma – (Fallacy) Ignoring or disregarding other options and possibilities Conditional Material Implication Implication The relation that holds between the antecedent and the consequent of a conditional If P then Q (P is the antecedent and Q is the. If P then Q, Q, therefore P Using our standard translation manual, we can evaluate them both with the following truth table P Q P → Q Q P → Q P T T T T T T T F F F F T F T T T T F F F T F T F For the first argument, the premises are all true only in row 1, and the conclusion, Q, is also. Therefore, the argument must be valid 5 Valid We can test for validity by substituting statement variables into the argument If we do the substitution, we get If p, then q Not q Therefore, not p Upon inspection, we find that this is one of the common patterns of valid inference discussed above—modus tollens.
But if Q →R and ~R are both true, then ~Q is also true For ~Q follows from Q →R and ~R, in virtue of modus tollens So, if the premises are all true, then so is ~Q That means that all the following formulas are true – P →Q, Q →R, ~R, ~Q So, in particular, P →Q and ~Q are both true But if these are true, then so is ~P (the. If P is false, then ¬P is true P∧ Qshould be truewhen both P and Qare true, and falseotherwise P Q P∧ Q T T T T F F F T F F F F P∨Qis trueif either P is trueor Qis true(or both — remember that we’re using “or” in the inclusive P Q R P → Q ¬R (P → Q) → ¬R T. Therefore either not p or not r Simplišcation (p∧q) ∴ p p and q are true;.
If P then Q If P then R It does not at all imply that If Q then R Why?. The part of a conditional statement (If p, then q) introduced by the word then Deductive Argument An argument intended to provide logically conclusive support for its conclusion. And the conclusion is p We then create truth tables for both premises and for the conclusion Again, since our argument contains two letters p and q, all of our truth tables should contain both p and q and should have all the rows in the same order Premise 1.
Therefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;. And if r then s;. Therefore, not q—is called modus tollens a True b False This argument form known as modus tollens is valid a True b False When you read a philosophical essay, you are simply trying to glean some facts from it as you might if you were reading a science text or technical report a True.
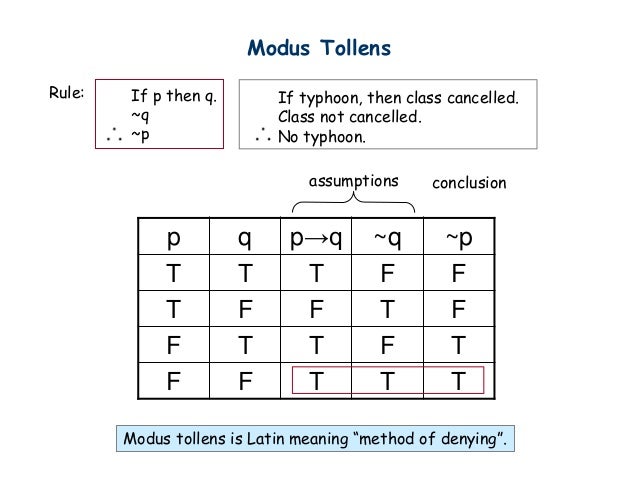
In propositional logic, modus tollens, also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference Modus tollens takes the form of If P, then Q Not Q Therefore, not P It is an application of the general truth that if a statement is true, then so is its contrapositive The form shows that inference from P implies Q to the negation. All that it is, is a claim that if P is true, then Q is also true — without making any more claims than this An alternative way of considering P ⊃ Q is as a constraint that. The argument form If p, then q q Therefore, p is Invalid An argument intended to provide probable support for its conclusion is Inductive This argument—If Buffalo is the capital of New York, then Buffalo is in New York Buffalo is in New York Therefore, Buffalo is the capital of New York—is an example of.
Therefore either not p or not r Simplišcation (p∧q) ∴ p p and q are true;Therefore, q— is called modus ponens a True b False An argument of this form—If p, then q;If P then Q 2 P 3 Therefore, Q Valid (Modus Ponens) B 1 If P then Q 2 Q 3 Therefore, P Invalid This argument form is commonly mistaken as being valid Notice that even if the premises are true, the conclusion could still be. (pVq) V (~p^q) → q p q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18 (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a. Otherwise it is true Contrapositive The contrapositive of a conditional statement of the form If p then q is If ~q then ~p Symbolically, the contrapositive of p q is ~q ~p.
P → q = (~p ∨ q) In the Principia Mathematica, the = denotes is defined to mean Using this denotation, the above expression can be read p implies q is defined to mean that either p is false or q is true The following truth table shows the logical equivalence of If p. If P, then Q Therefore, if not P, then not Q which may also be phrased as → (P implies Q) → (therefore, notP implies notQ) Arguments of this form are invalid Informally, this means that arguments of this form do not give good reason to establish their conclusions, even if. As far as I understand, If p then Q means if P is true, Q has to be true Any other case, I don't know So, from what I understand, the first 2 rows of the truth table state that If P is true and Q is true, the outcome is correct and If P is true and Q is false,.
If P, then Q Q is false Therefore, P is false In logical operator notation where represents the logical assertion Or in settheoretic form ∴ (P is a subset of Q x is not in Q Therefore, x is not in P) The argument has two premises The first premise is the conditional ifthen statement, namely that P implies Q. P = it rains / is raining q = the squirrels hide / are hiding ' 05Œ09, N Van Cleave 1 Rewriting the Premises and Conclusion Premise 1 p → q Premise 2 p then Brad sings in the choir Therefore, Brad sings in the choir ' 05Œ09, N Van Cleave 33 If. Answer (1 of 4) I don’t know if this particular argument has a name, but it’s a direct consequence of the law of excluded middle (LEM) which states that for all propositions p, p \lor \lnot p holds If you have p \lor \lnot p then you also have p \lor \lnot p \Rightarrow q for all q and, consequ.
Therefore if p is true. QUESTION 66 If p then q Therefore p A Valid, affirming the antecedent O B Invalid, fallacy of denying the antecedent O C Invalid, fallacy of uncertain relation between premises O D Invalid, fallacy of affirming the consequent. P → q q Therefore, p This argument has two premises p → q;.
Because if P is false, the first two would be (vacuously) true, but it might be that also Q is true and R is false, which would make the last one false!. After awhile, it does indeed become obvious. The writer assumes that you know when if P, then Q is false The writer also assumes that you know getting a contradiction from assuming if P, then Q is false means that if P then Q must be therefore be true Why waste words on explaining the obvious?.
If p then q;. Logically they are different In the first (only if), there exists exactly one condition, Q, that will produce P If the antecedent Q is denied (notQ), then notP immediately follows In the second, the restriction on conditions is gone The usual rules apply, and nothing follows from denying the antecedent Q Share Improve this answer. Therefore, P and Q Therefore, Q and P Hypothetical Syllogism (HS) 1 If P, then Q 2 If Q, then R 3.
“Therefore, I will study databases or I will English literature”. For example there is no necessary connection between P='22=4' and Q='Washington is the capital of USA',still the inference P >. The conditional of q by p is If p then q or p implies q and is denoted by p q It is false when p is true and q is false;.
QUESTION 1 Modus tollens has this argument pattern The correct option for this question is If p, then q Not q Therefore, not p It is because in Modus Tollens p and q are prepositions Modus Tollens states that if p implies q, and q is false, View the full answer. Noticethat this leaves with some area of the Qcircle that is not also in the Parea That is because if P then Q does not mean that there cannot be instanceswhere Q is true, but P is false An important thing to notice, however,is that if you say that. It is convenient to read → sentences in English using if then That is, we read P → Q ( “P arrow Q”) as if P, then Q But there are many other ways in English of saying the same thing, and hence many other ways of reading → sentences in English Q if P P only if Q Q provided that P Q in case P Provided P, Q In the event that P, Q.
Is rational Then 2 = p/q for some integer p and q with q ≠ 0 and gcd(p,q) = 1 Since 2 1/2 = p/q, we know (p/q)2 = 2 (ie, square root of 2, to the power of 2) Then we get (p/q) 2 = p 2 /q 2 = 2, and p 2 = 2* q 2 So p 2 is even Let p 2= 2k for some integer k So p 2 = (2k) = 4k 2, which is equal to 2* q Dividing both sides by 2, we get 2k 2 = q 2 Since k 2. Suppose P If P, then Q But Q is absurd (ie implies a contradiction) Therefore, P is false (or not the case) Anselm begins with a stipulative definition of “God” as “a being than which no greater being can be conceived” The argument of Proslogium (Ch II) (1) God exists in the understanding but not in reality (Supposition).
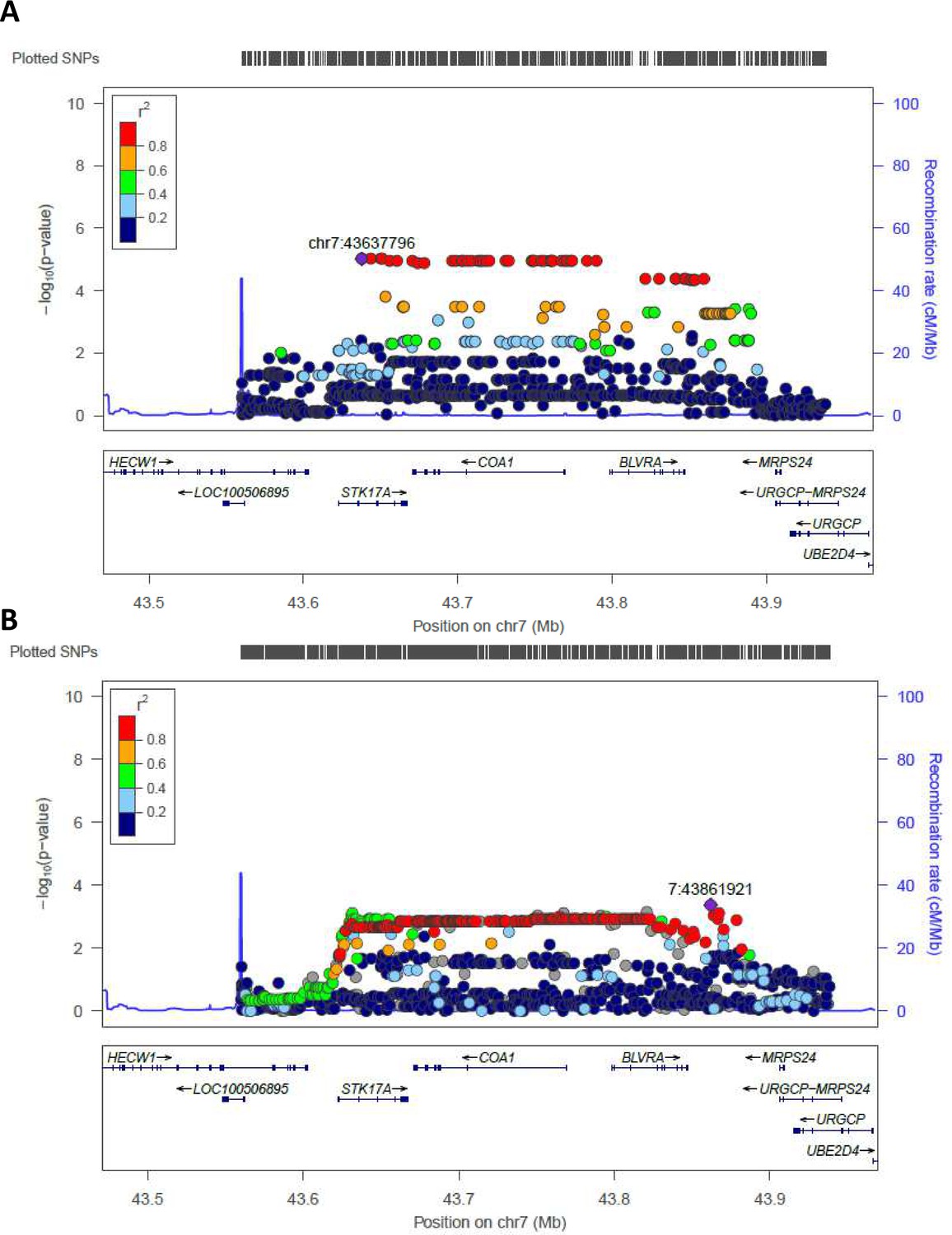
Whole Genome Sequencing Analysis Of Semi Supercentenarians Elife
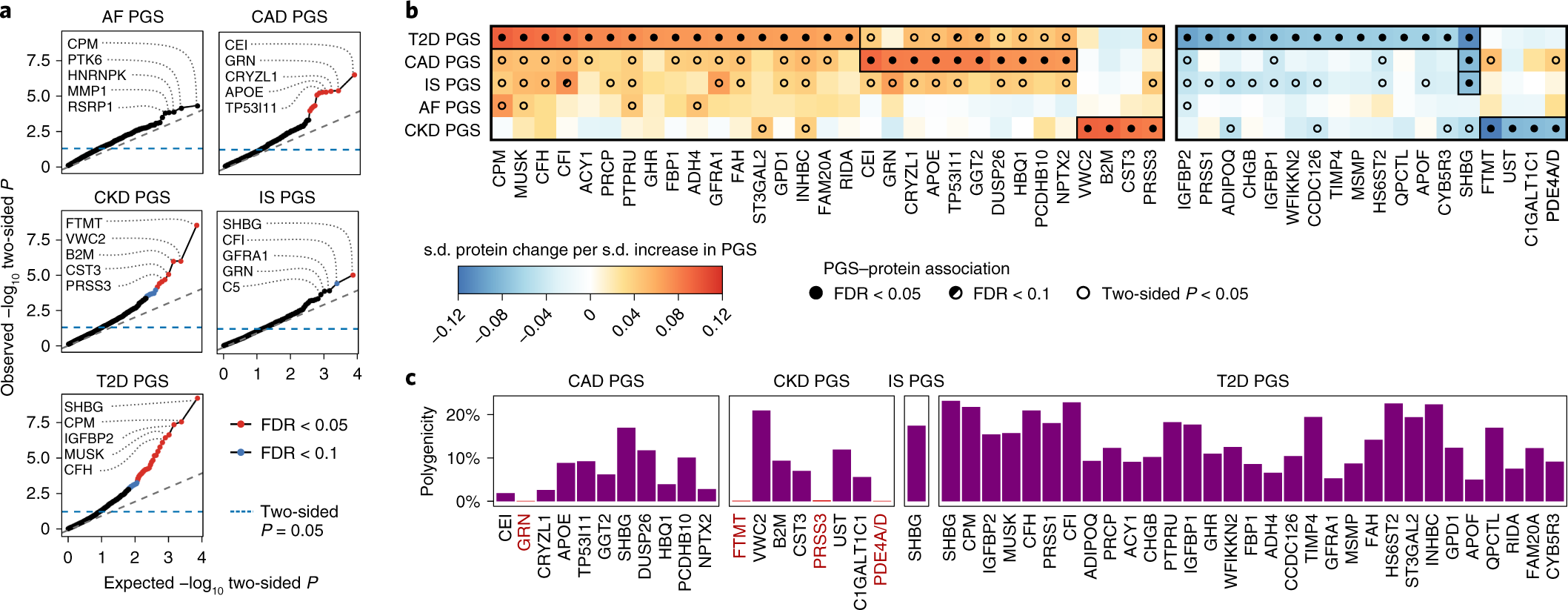
Integrative Analysis Of The Plasma Proteome And Polygenic Risk Of Cardiometabolic Diseases Nature Metabolism

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero
If P Then Q Q Therefore P のギャラリー
Inf Ed Ac Uk

In Praise Of Rationality The New York Times

17 Types Of Similarity And Dissimilarity Measures Used In Data Science By Mahmoud Harmouch Towards Data Science

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero

Exercises Questions And Activities Pages 1 19 Flip Pdf Download Fliphtml5
1

Solved 2 For Each Of The Arguments Below Decide Whether Chegg Com

Ppt Deductive Reasoning Powerpoint Presentation Free Download Id

Ppt Essential Deduction Powerpoint Presentation Free Download Id

End Of Chapter 3 Critical Thinking
Dspace Mit Edu

Ppt Components Of Barriers To Critical Thinking Powerpoint Presentation Id

13 Logic And Reasoning Ideas Logic Inductive Reasoning Philosophy

Chapter 1 Random Experiments Notes For Probability

Ii If P Then Q Q Therefore P Can You Name This Form The Above Type Of Argument Course Hero

Solved Question 7 1 Point The Argument Form If P Then Q Chegg Com
6 Conditional Derivations A Concise Introduction To Logic

Some Other Logical Forms
Numdam Org

Introduction To Philosophy Smu Fall 16 Tools

1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download
Jstor Org
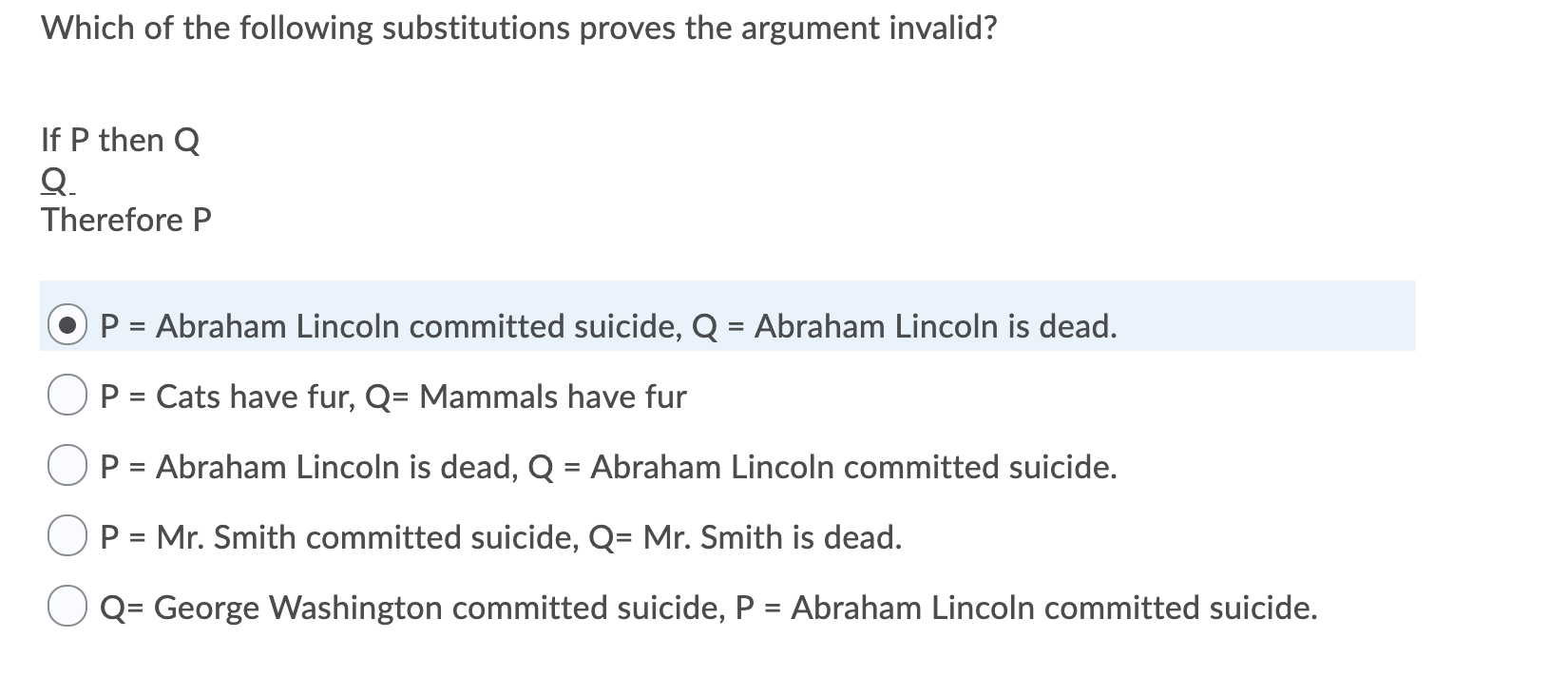
Solved Which Of The Following Substitutions Proves The Chegg Com

Inductive Reasoning Definition Basing A Conclusion On Specific Examples Examples All Crows Are Black The Sun Will Rise Tomorrow Pdf Free Download

Chapter 22 Common Propositional Argument Forms Introductory Remarks P 2 This Chapter Introduces Some Of The Most Commonly Used Deductive Argument Ppt Download

Solved Iphone 6 Compass Is Unworkable Share Phone Repair Guide And Provide Phone Repair Tools China Phonefix Shop Team Vipprogrammer Com

Ppt Verifying Arguments Powerpoint Presentation Free Download Id

Autodidacticism

Phi 1101 Lecture Notes Fall 14 Lecture 15 Modus Tollens Modus Ponens Hypothetical Syllogism
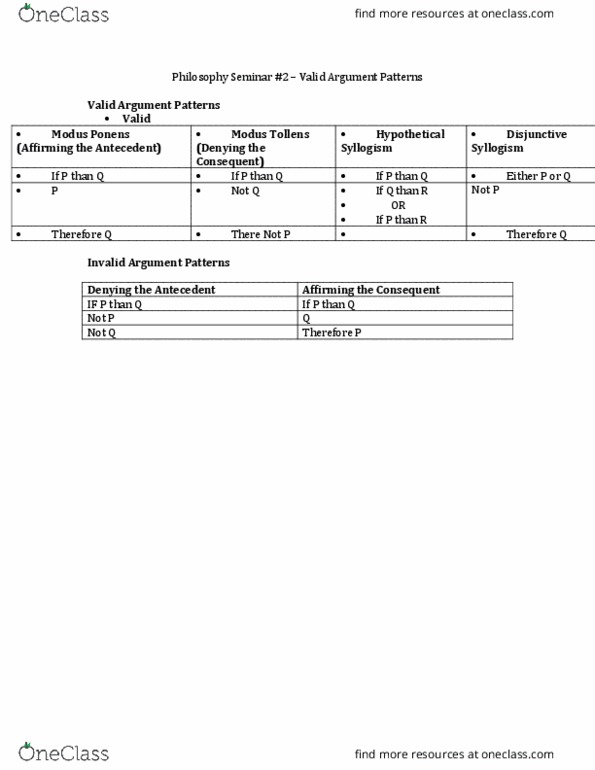
Class Notes For Phil 2100 At University Of Guelph U Of G

Phil 210 Logical Fallacy Logical Fallacy An Argument That Is Structurally Invalid Because Its Studocu

Phl134 Lecture Notes 1 12 Week 1 Tutorials Hypothetical Syllogism Valid If P Then Q If Q Then Studocu

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download

Critical Thinking Study Guide Study Guide Terms Antecedent The First Factor Upon Which The Studocu

Ii If P Then Q Q Therefore P Can You Name This Form The Above Type Of Argument Course Hero

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download
Psychologie En Wetenschap Week 2 6461ps012 Studeersnel

Tricky Phil 105 Things Flashcards Quizlet

Pdf Rules Of Logical Inference Dr Jason J Campbell Academia Edu

Is P Land P To Q To Q A Tautology Mathematics Stack Exchange

Solved Question 11 1 Point The Valid Argument Form Known Chegg Com

Philosophy Logic And Logical Arguments Ppt Video Online Download

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero

Solved Which Of The Following Substitutions Proves The Chegg Com

Philosophy Logic And Logical Arguments Ppt Video Online Download
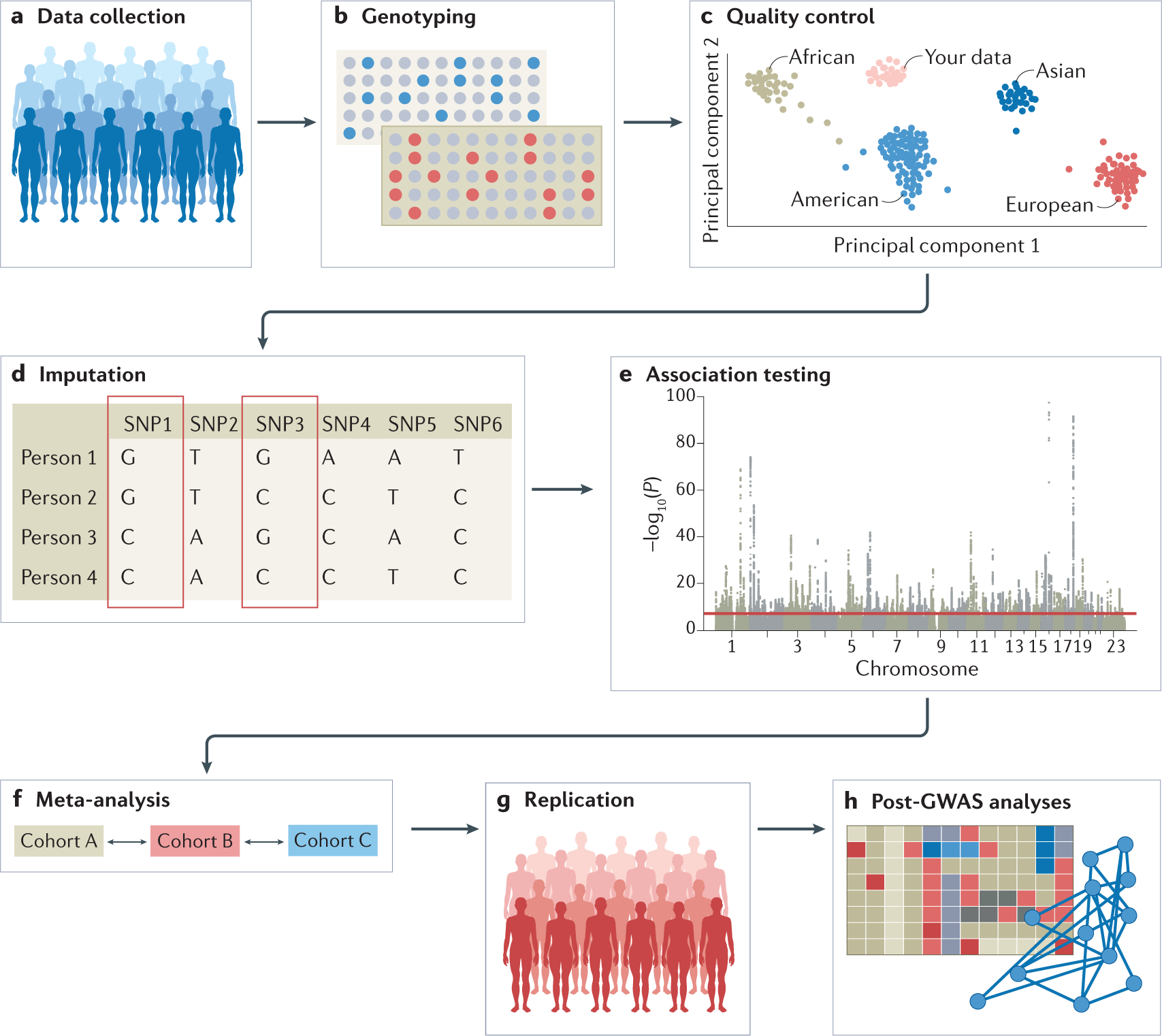
Genome Wide Association Studies Nature Reviews Methods Primers

Logic Propositions N N A Proposition Is A

Soc Sci 3a Lecture Notes Fall 16 Lecture 2 Modus Tollens Modus Ponens Motal
Open Uwi Edu

2 3 Methods Of Proof Ppt Video Online Download

Ppt Deductive Validity Powerpoint Presentation Free Download Id
1

Ii If P Then Q Q Therefore P Can You Name This Form The Above Type Of Argument Course Hero
Mathematical Logic Part 2
Sciencedirect Com

Math 1030 Exam 1 Review Strawman Distorted Version Of P Is True Therefore P Is True Appeal To Studocu
Royalsocietypublishing Org

1 Introduction To Abstract Mathematics Valid And Invalid Arguments 2 3 Instructor Hayk Melikya Ppt Download
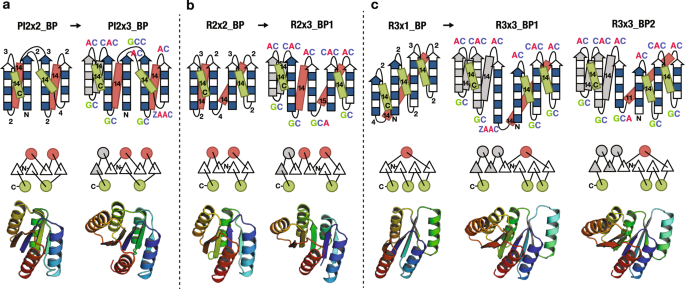
Role Of Backbone Strain In De Novo Design Of Complex A B Protein Structures Nature Communications

Questions With Answers In Pure Mathematics Science Topic

Solved Which Of The Following Are Valid Logical Arguments Chegg Com

Logical Arguments Modus Ponens Modus Tollens Youtube

1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download

Introduction To Philosophy Smu Fall 16 Tools

Propositional Logic Conditional Statement If P Then Q
Propositional Logic Conditional Statement If P Then Q
Projecteuclid Org

Faith And The Philosophy Of Science Hebrew For Christians
Projecteuclid Org

Ppt Logic Powerpoint Presentation Free Download Id

Solved Consider The Argument Form P Rightarrow Tilde Q Q Chegg Com

Logical Fallacies Logical Fallacies Are Statements That May

Set Operations And The Laws Of Set Theory Binary Operations After Learning How To Count A Student Usually Uses Methods For Combining Counting Numbers First This Is Accomplished Through Addition Usually The Student Uses The Universe Of Positive Integers

Reasoning And Critical Thinking Ppt Download

Chapter 22 Common Propositional Argument Forms Introductory Remarks P 2 This Chapter Introduces Some Of The Most Commonly Used Deductive Argument Ppt Download
Affirming The Consequent

Philosophy 103 Linguistics 103 Yet Still Even Further

In Praise Of Rationality The New York Times
Is P Land P To Q To Q A Tautology Mathematics Stack Exchange

C81cog Cognitive Psychology 1 Syllogistic Reasoning Dr Alastair D Smith Room B22 School Of Psychology Ppt Download
Know Your Logical Proofs Smbc R Comics

Evaluating Philosophical Claims And Theories Ppt Video Online Download

Arguments Identifying Ordering Premises Premises Reasons Premises Reasons

Solved 23 If Pvq Is True Then Q P Must Be 24 If P Q Chegg Com

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download

17 Types Of Similarity And Dissimilarity Measures Used In Data Science By Mahmoud Harmouch Towards Data Science

The Limitation Of The Scientific Method A Man After God S Own Heart

Critical Thinking Phil 210 Ec Lesson 4 Fallacies From Lecture Studocu
10 Points Question 1 Consider The Following Argument Chegg Com

In Praise Of Rationality The New York Times
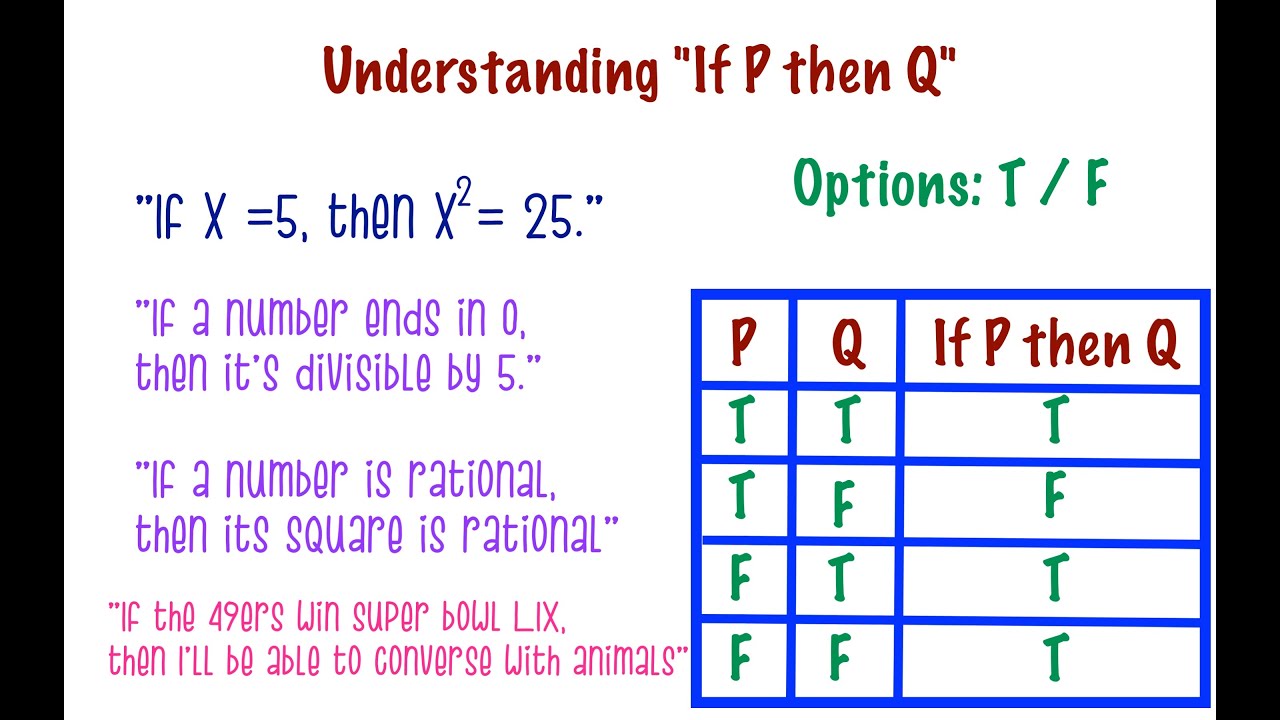
Understanding If P Then Q Youtube

1 Cpan 110 Week 9 Module 1 Creating Valid Arguments Diagramming Arguments Ppt Download
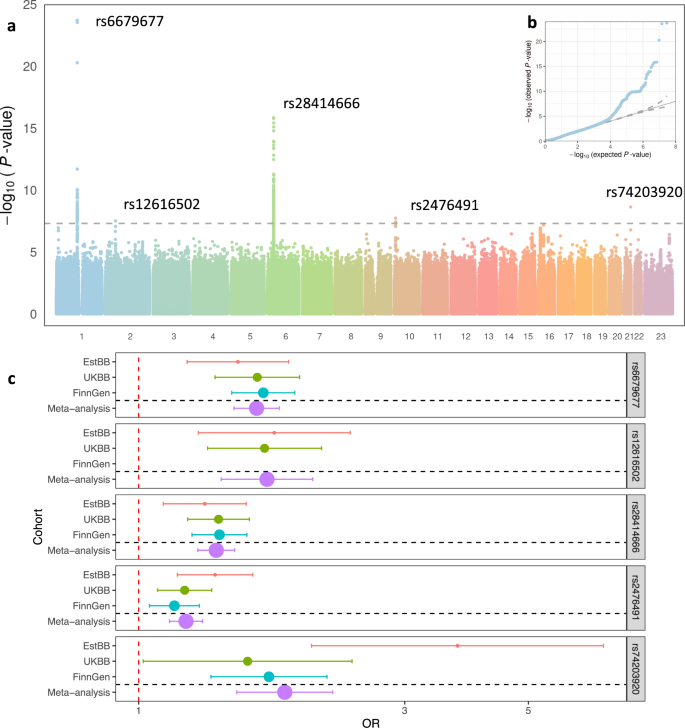
Genome Wide Association Study Identifies Five Risk Loci For Pernicious Anemia Nature Communications
Lec18 Pdf Google Drive

Philosophy 103 Linguistics 103 Yet Still Even Further

A Successive Conditionalization Approach To Disjunctive And Syllogistic Reasoning Semantic Scholar

Pdf Why Circular Reasoning Leads To Weak Theories And How Open Science Can Help Semantic Scholar

Solved If Pete Is Correct Then Sam Is Wrong It Is Not The Chegg Com
Prob Docx

Logic Propositions N N A Proposition Is A




