平面 点 距離
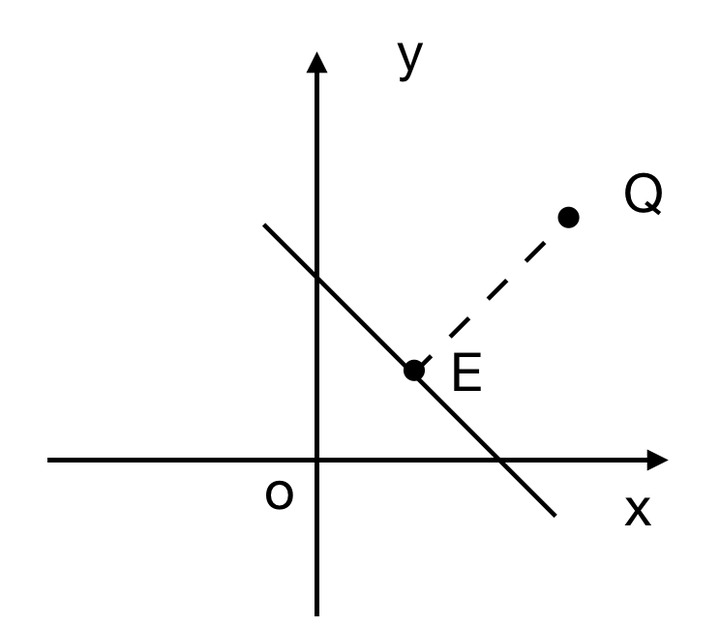
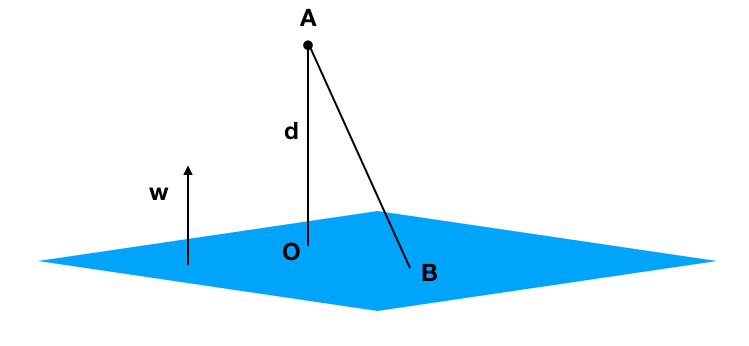
点と超平面の距離の導出 点 X(~x) X ( x ~) から超平面に下ろした垂線の足を H (h) H ( h) とします。 すると、ベクトル −− → H X = ~x –h H X → = x ~ – h は超平面に垂直なので、超平面の法線ベクトル w w に平行です。 よって、実数 k k を用いて下記と表現できます。 ~x –h = kw ∴ h = ~x –kw x ~ – h = k w ∴ h = x ~ – k w ここで、 H (h) H ( h) は超平面 wTx b = 0 w T x b.

平面 点 距離. 2点間の距離を座標平面で考える まずは座標平面上にある 2つの点の間の距離 を求める公式を作っていきましょう。 作るといっても難しいことはありません。 三平方の定理 さえあればすぐに求めることができます。. 座標平面上の最短距離 解説 次の図のように,座標平面上に2点a,b が このように,複数の点を結ぶ線分の長さが最短となるためには,それらの点が一直線上に並ばなければいけませんが,結んだ線分の中継点(点p)に対して端の点(点a,b. 曲率 (t をパラメータとする場合) フレネ・セレの公式.
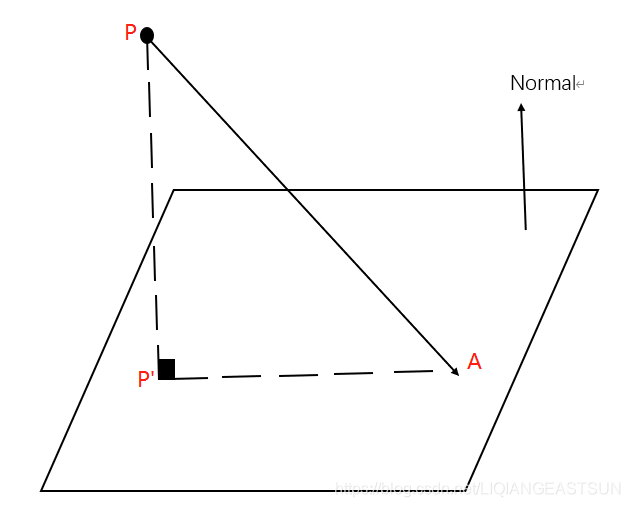
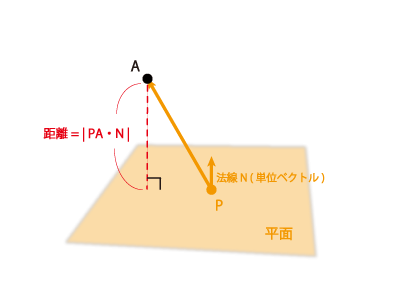
原点と平面との距離は $0$ であり、平面は原点を通過する(下図)。 以上のように $h$ は、法線と射影点 $\mathbf{x}_{0}$ の位置が同じ向きである場合には、 一方、反対向きに場合には、距離 $H$ にマイナスの符号を付けた負の値になる。 このような意味で、$h$ を 符号付き距離と呼ぶ。 3点を通る平面 3点 $A, B, C$ を通る平面の方程式は、 である。 $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$. その絶対値が点と平面の距離 return abs( dot_product( N, PA ) );. 移動距離がこれより短くなることはありません。なので、直線 $\ell$ と線分 AB との交点を通ることがわかります。 このように、2点間の移動距離が最小になるのは、2点を線分で結んだときとなります。これが最短経路の問題のポイントとなります。.
点と平面の距離公式は 点と直線の距離公式の3通りの証明 で解説した公式のの三次元バージョンです。 証明は二次元の場合の証明(三通りいずれでも)をそのまま三次元に拡張するだけでできます。 証明1の三次元への拡張が簡潔で有名な証明なので解説します。 証明2については拡張の際に面積を求める部分で工夫が必要になり面白いので解説します。 証明3については二次元の場合と. 平面(1)上にある1点と(2)の間の距離を求めればよい. 平面(1)上のどの点からでも同じ距離になるので,どの点から求めてもよい. たとえば,(1)において x=0, y=0 とすると, z−5=0 より z= となるから,点 (0, 0, ) は(1)上にある.. 2直線の距離 3点を含む平面の式 4点で形成される四面体の体積 点と平面の距離 直交座標から球座標へ変換 直交座標から円柱座標へ変換 球座標から直交座標へ変換 球座標から円柱座標へ変換 円柱座標から直交座標へ変換 円柱座標から球座標へ変換.
点Bに測角儀を移して、前点(A)から次点(C)までの角度 と、次点までの距離(BC)を測量する。 2 3 cの内角=80°16′15″ dの内角=153°1′25″ eの内角=93°1′55″ cd=7230m de=106m ea=7950m 各点(c、d、e)で前点から次点の角度と、次点までの距 離を測量する。. 点と直線の距離自体は座標上でなくても考えることができます. x y 平面上で考えた場合には以下のように 点と直線の距離を求めることができます. x y 平面上の2点 A ( p, q) と直線 ℓ a x b y c = 0 の距離 d は次で得られる. 「2点間の距離」とは違い,この「点と直線の距離」の公式の導出は少々面倒です. 導出法はいくつか考えられますが,ここでは素朴に最初に説明した 2点. 空間における点A(x 1,y 1,z 1)、点B(x 2,y 2,z 2)の距離は次のように求めることができます。 POINT z平面が加わったので、z座標についても同じように考慮しましょう。.
平面あるいは空間内にある2点間の距離を,点の座標によって表す数式です。 目次 具体例 2点間の距離の公式の証明 公式とみるか,定義とみるか? いろいろな距離 具体例 例 平面内の2点 A = (3, 3), B = (6, 7) A = (3,3),B = (6,7) の間の距離 d d は \begin {aligned} d &= \sqrt { (3 6)^2 (3 7)^2} \\ & = \sqrt { (3)^2 (4)^2} \\ & = 5 \end {aligned} d = (3− 6)2 (3−7)2 = (−3)2 (−4)2 = 5. ものすごく基本的なことですが、 土木平面図の測点表記noからno間の距離の算出する計算方法を教えて下さい noに小数点が入ると混乱してしまいます たとえばno~no1418=163m 計算式等があるのでしょうか? また、下記の場合の計算方法. 124 点の直線への正射影 35 125 点と直線との距離.
定理1 (点と平面の距離の公式) 点A(x0;y0;z0) と平面ˇ axby cz d = 0 の距離は jax0 by0 cz0 dj p a2 b2 c2 (11) (証明) 点A が平面ˇ 上にあるときは,ax0 by0 cz0 d = 0 なので,(11) は成立する 点A が平面ˇ 上にないとき,点A から平面ˇ に下ろした垂線の足をP(x′;y′;z′) とする!. 平面上の点は 座標が です。 求めたい点を とおいて、二点間の距離の公式を利用しましょう。 解答 (見切れる場合は横へスクロール) 求める点を点 とおく。 二点間の距離の公式から、 ① ② ③ より であるから、 ① = ②より ④ ② = ③より ⑤ ④、⑤より、 したがって、 答え: 以上で問題も終わりです! 二点間の距離について、理解が深まりましたか? 公式としては つ出てきましたが. 平面上の2点間の距離 このように平面上にある2点間の距離であっても、座標を用いれば求めることができます。 x軸方向の距離とy軸方向の距離については、 数直線上の2点間の距離 を利用してそれぞれ求めることができます。 ただし、これでは平面上の2点間の距離を求めたことにはなりません。 ここからさらに図形的に2点間の距離を求めます。 利用する図形的な知識は、 三平方の定.
図より,点z 1 と点z 2 の距離は,xy平面上の点A(x 1 ,y 1)と点B(x 2 ,y 2)の2点間の距離と等しいことがわかります。数学Ⅱで学んだ2点間の距離の公式より,点ABの距離は, AB=√{(x 2x 1) 2 +(y 2y 1) 2} となります。. 3次元空間における点と平面の距離 3次元空間における点 と平面 の距離は (証明) 平面 の法線ベクトル をその大きさ で割ると単位ベクトルになる. そこで,点 から,その単位ベクトルの何倍を継ぎ足せば平面 上にあるかを調べたらよい. この倍率tが求める距離になる . 点 が,平面 上にあるためには 距離は正の数だから 問題3 (選択肢の中から正しいものを1つクリック) ※解答すれ. 总结:平面解析几何主要的研究对象是直线与圆锥曲线,而 平面几何 主要的对象是直线以及由线段组成的 几何图形 ,因此在解析几何的问题中,往往使用平面几何的知识就能带来更加简洁的过程,同时,我们可以发现,即便是一个简单的问题,也会有许多不同的办法,每一种办法都是一个知识点.
平面上の2点(x1,y1)、(x2,y2)を入力し、それら2点間の距離を算出するプログラムを作成するのですが、√をプログラミングできません。以下のプログラムを教えて下さい x1:0 y1:0 x2:1 y2:1 この2点間の距離はです。. 平面上の点と直線の距離の公式,つまり ≪点 と直線 の距離d は, である。≫ は,数学Ⅱの2章「図形と方程式」の1節「点と 直線」で扱う。 2直線の垂直条件を扱った後にその公式が出て. 平面上の点の位置の表し方,および平面上の 2点間の距離の求め方について学びます。 − 45 − 高校講座・学習メモ ラジオ 学習メモ 第2章 図形と.
AP は,平面ˇ に垂直であるから,t をある実数として,!. 点到面的距离 已知平面 的方程为 ,空间任意一点 到该平面的距离 的公式为: 利用同样的做法,设从 做 的垂线得到垂足的坐标为 ,则很显然 为 的法向量, 也为 的法向量(后有证明),那么我们有: 又因为 在 上,因此有 ,代入上式即得:. AP = t 0 B @ a b c 1 C A 8 >> >< >> > x′ x 0=.
5 平面の方程式と内積,点と平面の距離の公式 例1 A(2,1,8) を通り, 2,n =(1, 3) r と直交する平面をπ, O からπに下ろした垂線の足をH とする. (1) π上の任意の点をP( , , )x yzとするとき,x,, yz の間の関係式を求めよ.. 点P1から点P2ベクトルのベクトルをS、点P1から点3ベクトルのベクトルをTとすると、 S = ( Sx , Sy, Sz) = ( x2x1, y2y1, z2z1) T = ( Tx , Ty, Tz) = ( x3x1, y3y1, z3z1) となる。 平面内のベクトルS とベクトルT の外積 (S×T)は2つのベクトルに直角となる ベクトルであり、平面の法線ベクトルと同方向. 点と直線の距離 座標平面上で、点 と直線 の距離 は で与えられる。 数学2の範囲でこれを証明しようとすると、かなりごちゃごちゃな計算をすることになります。 そこで今回はベクトルを用いることにしましょう。 (証明) 点 から直線 に下ろした垂線の足を とし、点 の位置ベクトルをそれぞれ とする。 また、直線 の法線ベクトルを とする。 は と平行なので ① となる が存在する。.
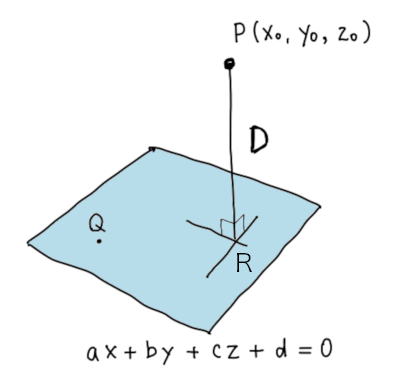
空間の点と直線の距離の公式について 高校では、空間の直線の方程式を (xa)/l=(yb)/m=(zc)/n と習います。空間での点と平面の距離の公式はチャートにも乗っているためわかるのですが、この直線と空間上のある1点の距離はどのようになるのでしょうか?. なぜこれで平面と点との距離が求められるのか、考えてみましょう。 点 P から平面に下ろした垂線の足を点 R とします。 平面と点P \((x_0,y_0,z_0)\) との距離 \(D\) というのは、PR の長さ \(\overline{PR}\) のことです。. それでは、平面上での2点間の距離について考えましょう。 すでに知っている人も多いですが、改めて考えてみます。 P(x1,y1) P ( x 1, y 1), Q(x2,y2) Q ( x 2, y 2) の2点間の距離を求めてみましょう。 PQ が x 軸に平行な場合や y 軸に平行な場合は、簡単ですね。 本質的には、 基本数直線上の2点間の距離 と同じ、一次元の話です。 x 軸に平行な場合は x2 − x1 x.
} //点Aと平面の距離を求める その2(平面方程式 axbyczd=0 を使う場合 ) double Distance_DotAndPlane2( const Vertex3D& A, const Plane& plane ). 110 点と直線の距離 点 P (p,q) と直線 lax by c 0 の距離 d は次の式で求めます. a 2 b 2 ap bq c d (110) 111 点から直線へ下した垂線の足 点 P から直線 l へ下した垂線の足 H は次のように求めます. まず,式(15)から,点 P を通り直線 l に垂直な直線 L.
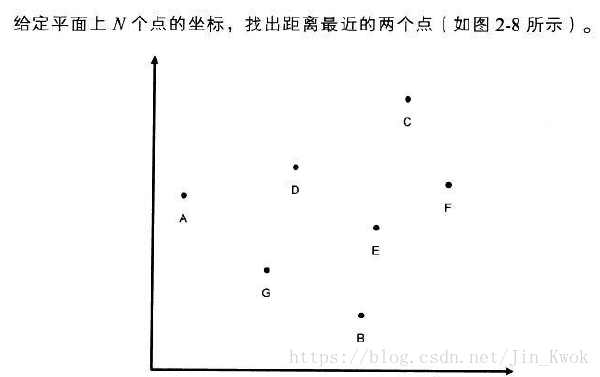
平面最近点对问题求解 基于java语言 Jin Kwok的博客 Csdn博客

平面方程法向量 夹角 点到平面的距离公式 路桥人学习网 道路设计院培训 鸿业纬地eicad海地视频教程

A点到b点距离公式 西瓜视频搜索
平面 点 距離 のギャラリー
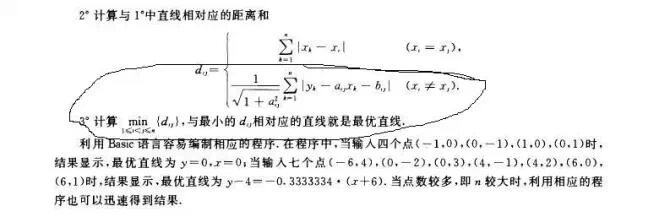
求助 关于平面上有限个点到直线的距离和最小的问题 先谢谢高手们 Cos论坛 统计之都 统计与数据科学论坛
几何间隔为什么是点到平面的距离 祥瑞哈哈哈 博客园

点到面的距离公式是什么怎么求 高三网

求点到平面的距离的方法 百度经验

空间中任一点到超平面的距离公式的推导过程 Chaolei3的博客 Csdn博客

平面直角坐标系平面两点间距离公式直角坐标平面内的两点间距离公式 学习岛

点到超平面的距离公式

平面直角坐标系难点突破 2 两点距离 八 九年级 每日头条

求点到平面的距离 C Monkeyfree 程序员宅基地 C语言求某点到平面的距离d 程序员宅基地
S01e04 点到平面的距离 掘金

空間中的平面方程式 點到平面距離公式說明 Youtube

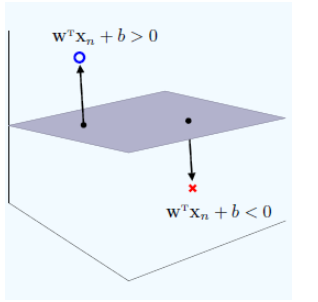
感知机 点到超平面距离推导 简书

两平面的夹角及点到平面距离公式 百度经验

高考数学 考试题型讲解 点到平面的距离 网易公开课

Svm 任意点到超平面的距离公式 这世界缤纷多彩 Csdn博客 点到超平面的距离

来个线性代数流风格地推导点到平面的距离 知乎

空間平面距離比 信欣茗數學園地 隨意窩xuite日誌

从点到平面的距离png图片素材免费下载 图片编号 Png素材网

点到平面的距离题 三人行教育网 Www 3rxing Org
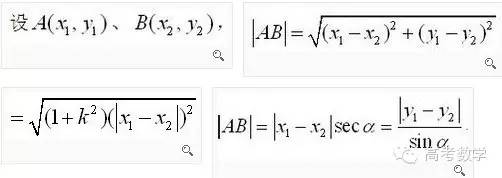
公式 两点间距离公式

高中数学 点到平面的距离的求法 方法
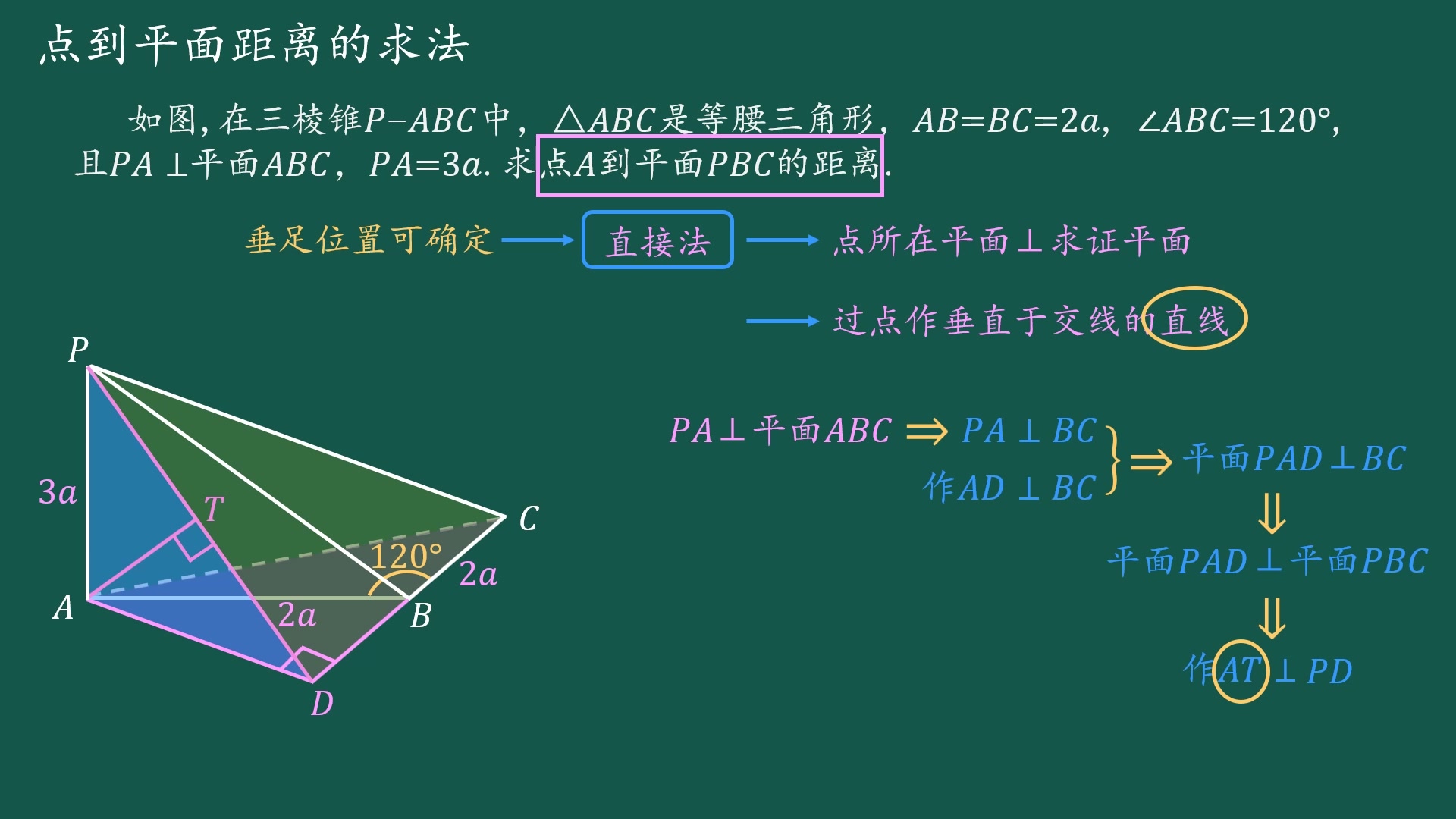
高中数学必修2 直接法求点到平面距离 基础 空间距离的计算 哔哩哔哩 つロ干杯 Bilibili

高数点到直线距离公式和平面束方程 Ppt 皮匠网

29 點到平面的距離公式 Youtube

平面方程与点到平面的距离 西檬饭 Csdn博客 点到面的距离
点到直线和点到平面的距离 四都教育

平面上兩點的距離 Math Distance Between Two Points On A Plane Youtube

高考数学点到平面距离公式点面距 哔哩哔哩 Bilibili
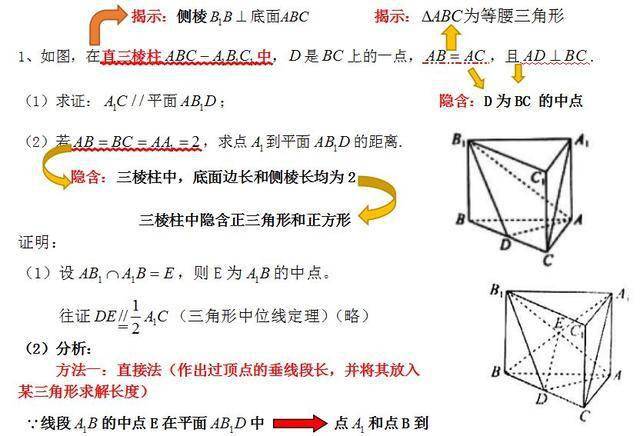
高中数学 点到平面的距离的求法 方法
两点间距离公式 快懂百科

求点到超平面的距离 Lawsonabs的技术博客 51cto博客

点と平面の距離の公式 証明と具体例 理数アラカルト

两平行平面间的距离 Mobe605af的技术博客 51cto博客
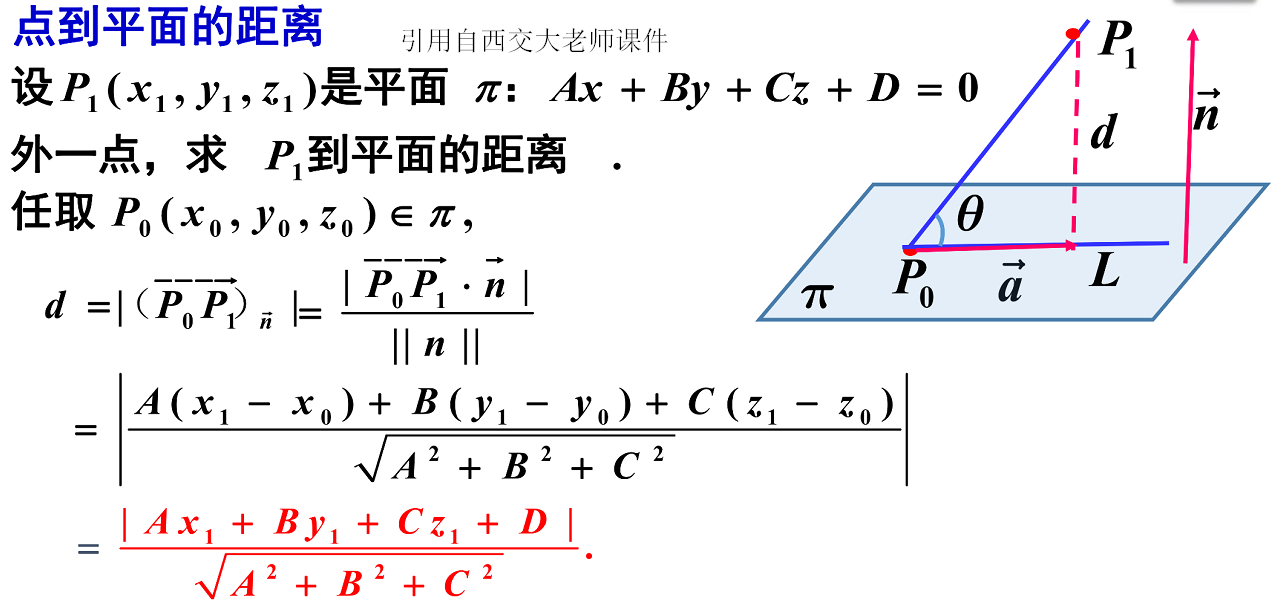
支持向量机 一 总述 点到平面的距离 Lagrange函数 Lagrange对偶 猴子吃果冻 博客园

10分钟掌握平面直角坐标系两点间距离公式与中点公式 哔哩哔哩 Bilibili

空间向量点到面数学 空间向量点到平面的距离公式是什么

如何确定点到平面的距离 数学21

求点到平面的距离的方法 百度经验

求点到平面的距离 C Monkeyfree 程序员宅基地 C语言求某点到平面的距离d 程序员宅基地

计算几何 平面上 点到线段的最短距离矢量法 程序员大本营
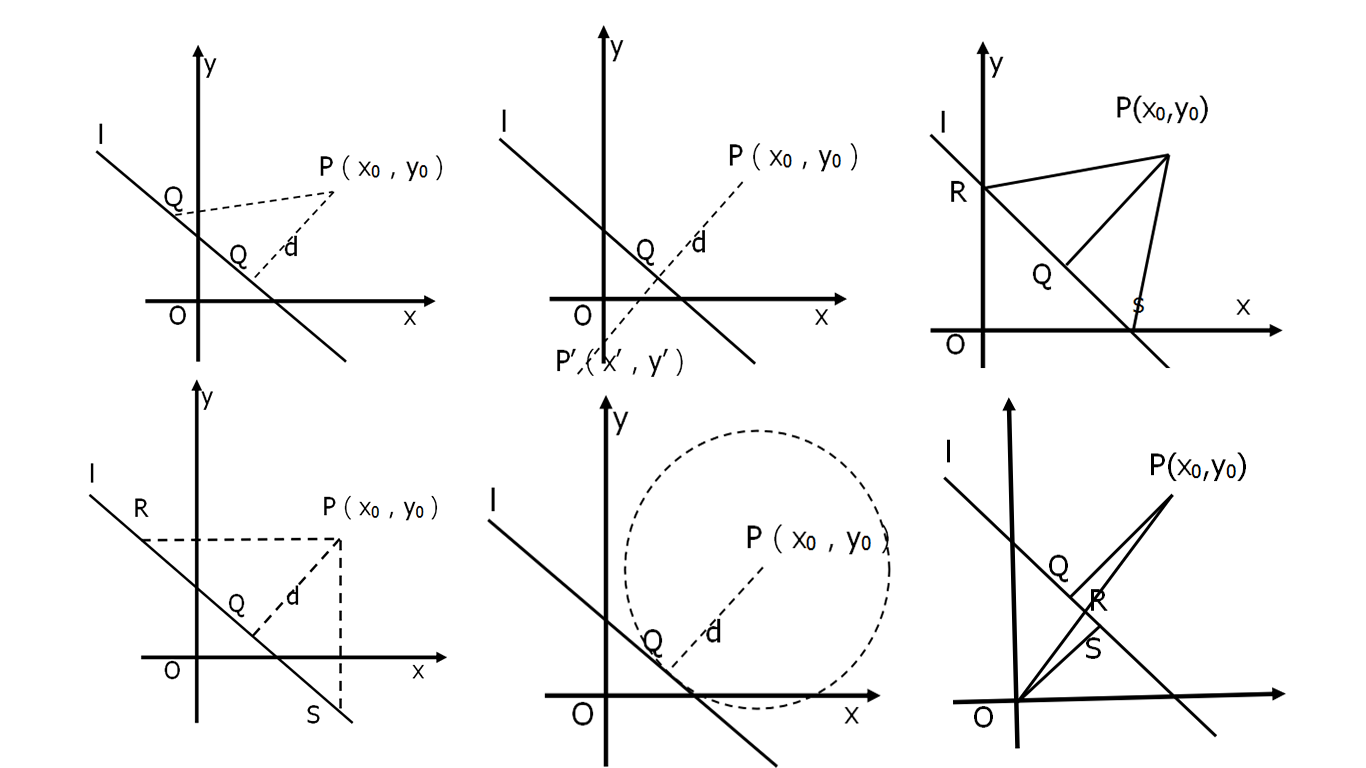
点到直线距离公式的几种推导 知乎

空间点到平面的距离 Page56 沪教版高三数学拓展二 理科 电子课本 教材 教科书 好多电子课本网
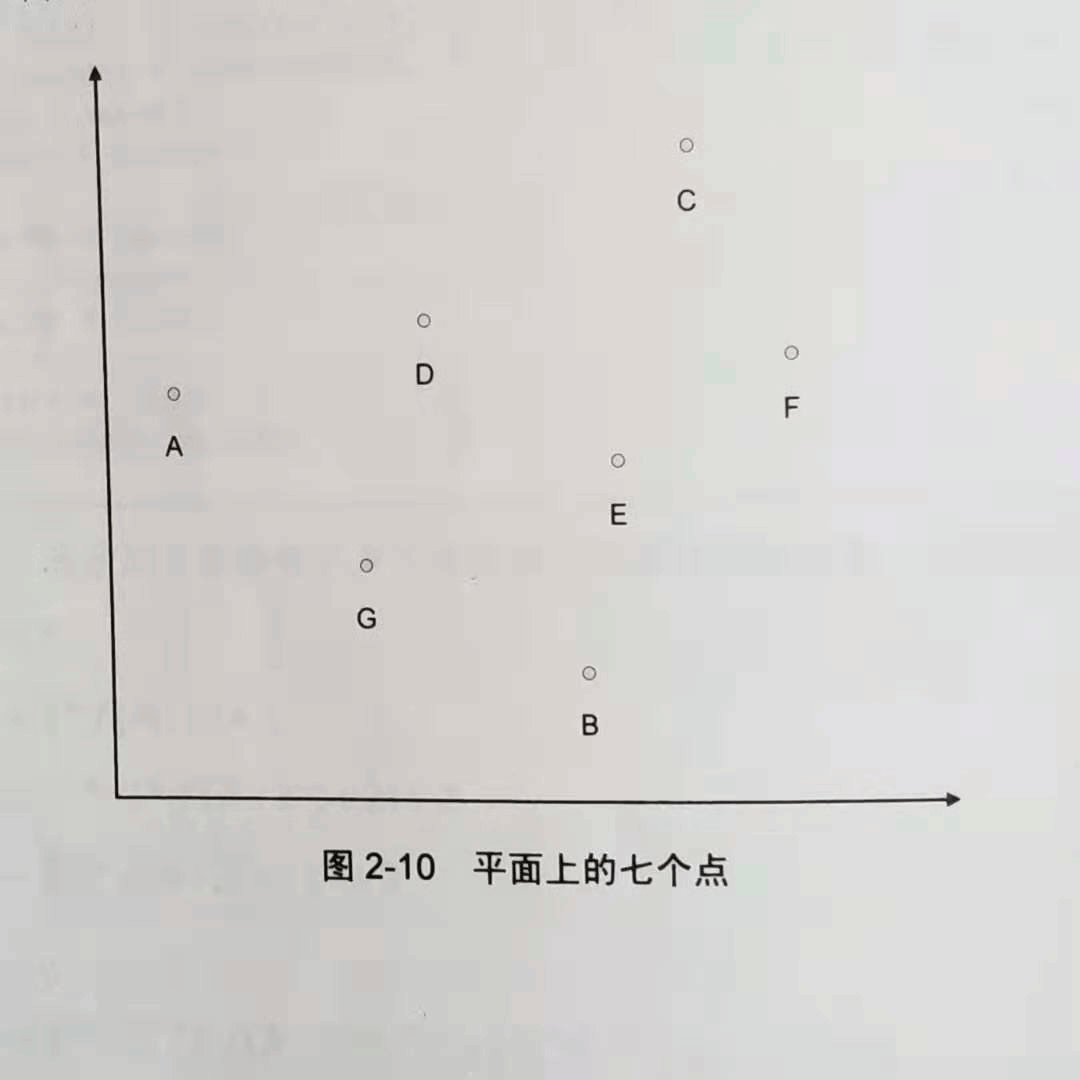
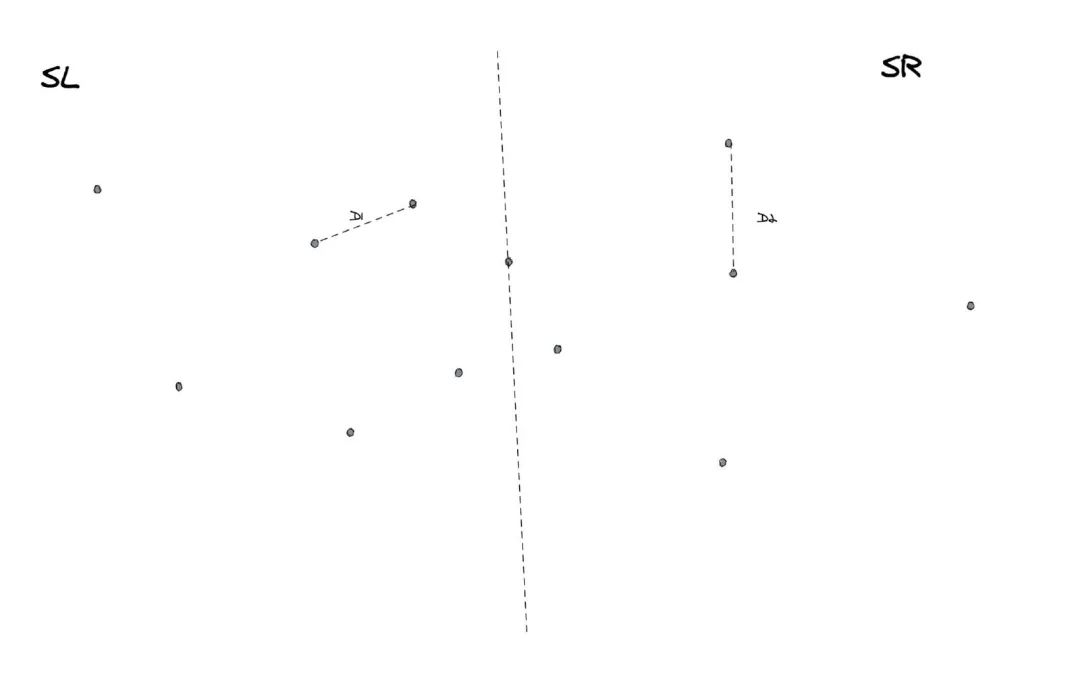
平面点集中距离最近的点对 東木 随笔
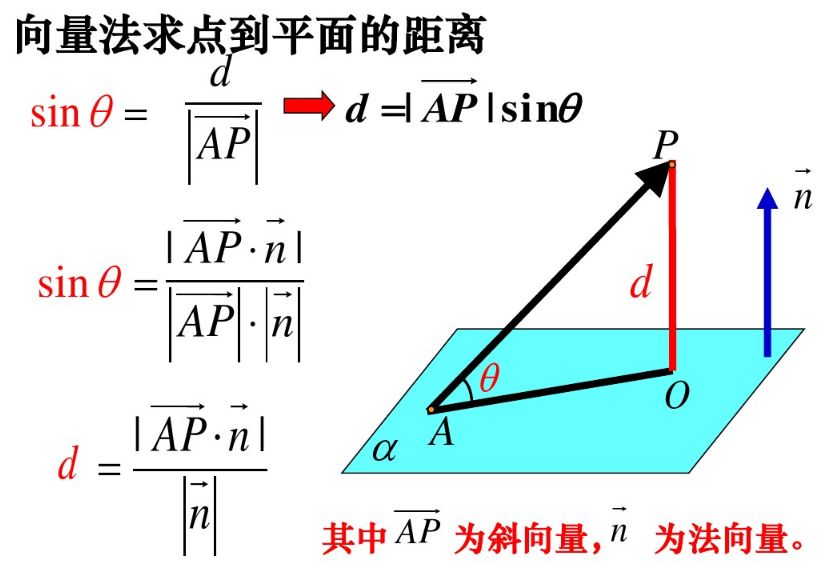
如何用法向量求点到平面距离 立体几何 用空间向量求点到面的距离 Suvo Sarkar的博客 Csdn博客
平面解析几何 坐标系与直线 Tbyangz S Blog
地图上两点间直线距离最短可能是错的 腾讯新闻

平面直角坐标系平面两点间距离公式直角坐标平面内的两点间距离公式 学习岛

点到平面距离 搜狗百科

如何从二维平面n个点中寻找距离最近两个点 Mb5fe的技术博客 51cto博客

空间两点距离 三维空间座标两点间距离公式 三人行教育网 Www 3rxing Org

点面距 会求吗 每日头条
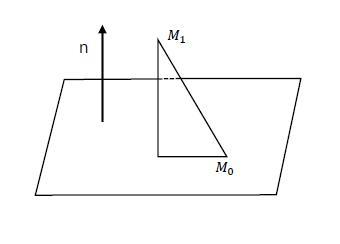
点到平面距离 搜狗百科

点と平面の距離公式の証明 数学b 空間図形の方程式 Youtube

用坐标计算两点距离 西瓜视频搜索

29 點到平面的距離公式 Youtube
点到平面的距离公式 搜狗图片搜索

点到平面的距离计算 Hunter Pcx的博客 Csdn博客 点到平面距离

距离 Gitbook
点到平面的距离 球与平面相交检测 Lq Csdn博客
平面内有n个点 如何快速求出距离最近的点对 Zglg的个人空间 Oschina 中文开源技术交流社区

点到平面的距离公式 万图壁纸网

用坐标计算两点距离 西瓜视频搜索

如何理解超平面 简书

两平面之间的距离公式 扒拉扒拉

02 距离公式与中点公式平面解析几何初步 I 高中数学 Youtube
点到平面的距离distance Point To Plane Flexijet Stone 1

点到面的距离公式是什么怎么求 高三网
超平面与法向量 Jin Liang 博客园
点到直线和平面的距离 知乎

點到線的距離公式證明點到直線距離 百度百科 Pxmode

点到平面的距离公式 翰墨小生 博客园

Python实现点到平面的距离 Python知识

到两点距离之和为定值 求平面上到a 0 3 B 0 3 两点的距离之和为定值10的轨迹方程 三人行教育网 Www 3rxing Org

平面の方程式と点と平面の距離 おいしい数学

高等数学之求点到平面的距离

平面内有n个点 如何快速求出距离最近的点对 分治法 屈婉玲教材 Taoqick的专栏 Csdn博客

空间点到平面的距离公式推导过程 试推导空间坐标系中点到平面的距离公式 三人行教育网 Www 3rxing Org

点到平面的距离公式 高三网

平面坐标系中点到直线距离公式的证明思想

点到平面的距离 Weclome To Eipi10
点と平面の距離 ベクトル解析 基礎からの数学入門
点と平面の距離を求める方法
距离速度时间公式

平面方程法向量 夹角 点到平面的距离公式 路桥人学习网 道路设计院培训 鸿业纬地eicad海地视频教程
点到直线和点到平面的距离 四都教育

平面坐标系两点之间距离公式 扒拉扒拉
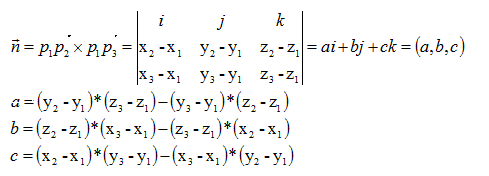
Math 转载 已知三点求平面方程 平面法向量和点到平面的距离
点到超平面距离 大专栏
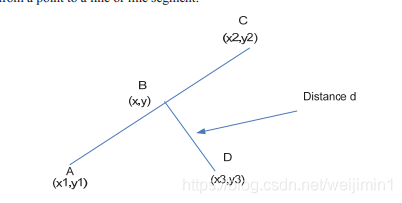
一种点到线段的最短距离的方法 Weijimin1的博客 程序员宝宝 点到线段的最短距离 程序员宝宝
线条和平面设计中的社交距离图标占用空间等待点标签孤立矢量图向量例证 插画包括有传染 小心

点到平面的距离公式推导 Jackie的博客 Csdn博客 点到平面的距离公式推导过程

19 年高中数学2 1 5平面上两点间的距离课时作业苏教版必修2下载 Word模板 爱问共享资料

求点到平面的距离的方法 百度经验

求点到平面的距离的方法 百度经验

点到平面的距离 Weclome To Eipi10

平面 数学名词 搜狗百科

Python计算平面点到平面直线距离向量 高等数学之向量代数与空间解析几何知识点与题型总结 不会唱歌了的博客 程序员宅基地

原创 平面内有n个点 如何快速求出距离最近的点对 Techflow1的技术博客 51cto博客




