分数 を 含む 方程式 解き方
もともとの下の式とあわせて考えてみると、 (上の式)×10 3x+5y=14 (下の式) x+y=4 あとは 下の式に3をかけて、xの係数を合わせれば解いていくことができる ね。 ③の答え (下の式)×6で、分数を消そう 下の式の 分数は先に整理 しよう。 1/2は邪魔だから、2をかけて消したい よね。 同じように、 1/3には3をかけたい 。 だから、 2×3の6を両辺にかければ、2つの分数は整理できる ね。.

分数 を 含む 方程式 解き方. 絶対値を含む方程式や不等式の問題の解き方も紹介していきますので、この記事を通してぜひマスターしてくださいね。 目次 絶対値とは? 絶対値の計算性質 性質①絶対値は常に正の数 性質②絶対値の 2 乗は中身の 2 乗 性質③絶対値の結合・分配;. その他(ライフ) 分数を含む方程式の解き方がわからない! こんにちは! ・3分の7x+34=5x-2 や、 ・9分の5x-32=-3 の解き方がわからなくて困ってます! 解き方を教えてください! 質問No. 方程式の解き方2 「両辺に同じ数字をかけても等式は成り立つ」 この性質を利用してxに係数がある方程式を解く。 xに係数があったら、 係数の逆数 をかけて1にする。 例 方程式 –3x = 12 の解き方 xの係数は 3 なので、 両辺に3の逆数をかけて 、両辺.
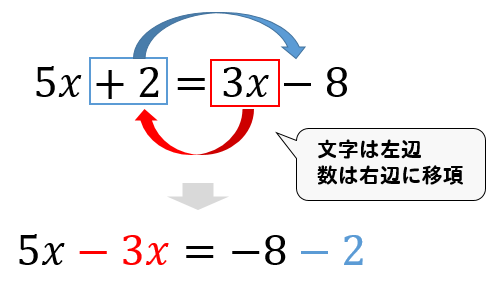
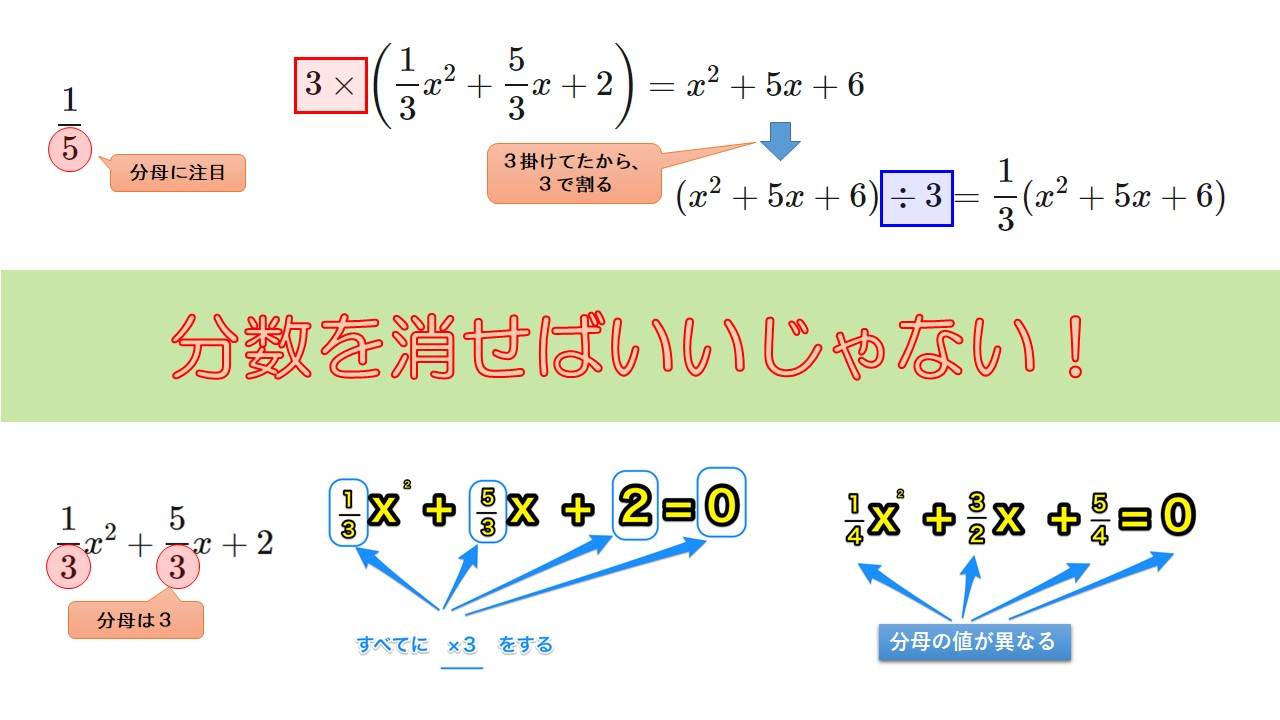
このように、方程式に分数があれば掛け算をして分数をなくしましょう! \(3\)で割らなくていいの? ここで、「\(3\)で割らなくていいの?」と思った方もいるかもしれません。 前に解いた、 $$\frac{1}{3}x^2 \frac{5}{3}x 2$$ の因数分解は、\(3\)を掛けたあと、元の大きさに戻すため最. 標準部分分数分解をしてから分数式を足す このサイトについて 数学の過去問の解き方や、数学の考え方を解説していくサイトです。 ご意見などはこちらへ。 広告 人気記事 基本平均値・中央値・最頻値はどう使い分ける? views 基本よく出る0度から180度までの三. 左辺から8を引くのであれば、右辺からも8を引かなければなりません。 2X+8−8=−12−8 −2X=− するとルールで学んだことを使います。 左辺の2が邪魔なので、両辺を2で割ってあげればいいんですね。 すると x=10 よって、解は10ということになります。 じゃあ、移項ってこんなに面倒なのかというと、これは本来の仕組みを説明しただけで、実際は.
1次方程式を解き方はシンプルです。 ・左辺に未知数x、右辺に数となるよう移項 ・「x=」の形になるよう、係数や項を整理 これだけです。実際に下記の計算問題を解きましょう。 2x3=7x 3x5=9x 前述した解き方に習って移項してください。1問目の答えは 2x3=7x 2xx=73 x=4 です。2問目. 方程式の問題の解き方(2):逆数をかける (例)方程式 2 x = 6 を解いてください これも方程式を解いてください、じゃから、「x = 」の形を目指すわけじゃな 数学おじさん そのためには、 まず、問題の式と、目的の式をよーく見比べてみてほしいん. 中1数学にでてくる1次方程式(xの方程式)の解き方 こんにちは!イボコロリを使ってみたKenだよ。 中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「 1次方程式 」とよばれているものだ。 なにせ、文字が1つしか含まれていないからね。.
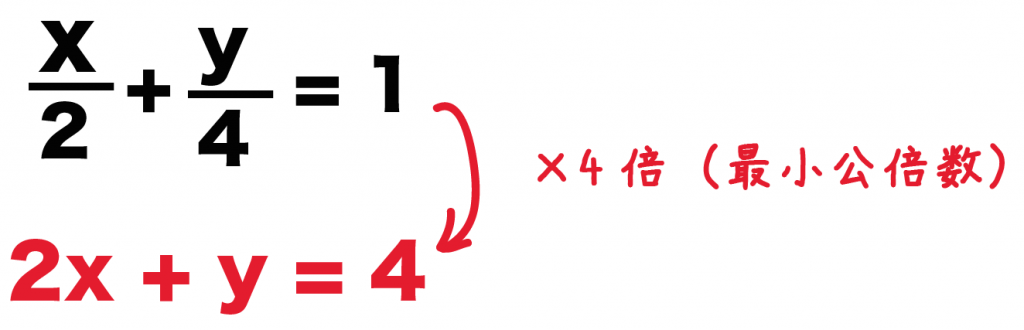
1字方程式の解き方 (1)少数・分数をふくむときは両辺に同じ数をかけて,係数を整数にします。 また,かっこがあったらかっこをはずします。 (2) x の項はすべて左辺に,数の項は右辺に移項します。 移項すると符号が変わります。 (3)両辺をそれぞれ計算して,ax=bの形にします。 (4)両辺を x の係数aでわります。 例題次の1次方程式を解きなさい。 (1)06 x +2=08 ここで紹介してい. 分数を係数に持つ方程式も 係数を整数にする のが基本で、分母を無くします。 連立方程式でも先ずは分母を無くすために、分母の最小公倍数をかけます。 上の方程式は 倍、下の方程式は 倍します。 最小公倍数をかけるのは できるだけ係数を小さくしたい だけなので公倍数なら何でも良いですよ。 最小公倍数が見つけにくい場合は、大きめの公倍数で良いです。 1次方程式のときよりややこしく見え. 分数を含む連立方程式 続いて分数のある連立方程式。 これも難しくない。 ポイントは同じ、「両辺を何倍かする」ことだ。 解き方 \begin{eqnarray} \left\{ \begin{array}{l} \frac{3}{4}x\frac{1}{2}y=3 \\ \frac{1}{2}x\frac{1}{6}y=5 \end{array} \right\end{eqnarray}.
分母にある数の 最小公倍数をかけて分母を消すべし! 分数を含む方程式は、そのままだと計算が難しいです。 そのため、まずは分母にある数の最小公倍数を両辺にかけて分数を無くしましょう。 例えば、このような方程式であれば分母にある数の最小公倍数12を両辺にかけましょう。 すると、このように分数が消えた式を作ることができます。 かず先生 最小公倍数のかけ算は必ず、す. 係数が分数の方程式 チェックテスト 例題・練習問題 カッコを含む方程式 カッコを含む方程式は 分配法則 でカッコを外してから解く。 例 15x2 (5x7) = 2x4 ←2を (5x7)にかけてカッコをひらく 15x10x14 = 2x4 ←数字を右辺、xの項を左辺に移項 15x10x2x = 414 ←左右それぞれの辺で計算 3x = 18 ←両辺を3でわる x = 6 分配法則でカッコを開くときには特に符号に注意。 上記の例で. 中3数学根を含む加法の解き方とは?同類項同士で計算する方法について解説します! 関連記事があります 中2数学多項式を簡単な形にする方法を解説! 中1数学逆数について解説!これが分かれば負の数を含む分数の割り算も怖くない! 中1数学文字を含んだ式に数字を「代入.
== 1次方程式の解き方(かっこ、小数、分数) == 1次方程式の解き方(まとめ) 小数、分数、かっこがあるときは、最初に処理しておきます。 1 係数に小数や分数があるときは、両辺を何倍かして整数係数に直しておきます。 2 「かっこ」があるときは、はずします。 上の処理が済んだら、次. 方程式の計算問題の説明は以上です。 数学はスポーツと同じで、例を見たあとに自分で問題を解いて計算方法を身につけていくものです。 問題に応じて等式の性質が反射的に出てくるまで、解いて解いて解きまくりましょう! なお、一次方程式の解き方. 指数方程式の解き方! 全5パターンを分かりやすく解説! 21年10月5日 「指数方程式の解き方が分からない」 「ルートや分数があって困っている」 今回は指数方程式に関するこんな悩みを解決します。 高校生 指数のある方程式が苦手で 以下のような指数に変数 を含む方程式を 指数方程式 と.
方程式の基本的な解き方の反復練習用にどうぞ( ^ ^)_ 真ん中から縦に折って、2回に分けて練習してもOK! 方程式 分数の形 No 1 方程式 分数の形 No 1 解答 方程式 分数の形 No 2 方程式 分数の形 No 2 解答 分数を含む方程式(係数が分数の方程式)、解くのが. 一次方程式(分数)の解き方まとめ 61 Share this 62 関連 ★一次方程式の分数★解き方は? 問題を使ってパターン別に解説するよ! 冒頭で述べたように、方程式に出てくる分数は消すことができます。 それはどういうことかというと等式の性質を利用したものです。. 分数がある方程式の解き方 次の方程式を解きなさい。 方程式に小数が含まれている場合 分母の最小公倍数を両辺に掛けて分数を消す! 今回の方程式であれば、分母にある3と4の最小公倍数である12を両辺に掛けます。 このように、分数の形を消すことができました。 ここまでくれば、基本通りの解き方でできますね。 分数がある一次方程式の解き方手順 分母の最小公倍数を両辺に掛け.
分数を含む方程式 係数に分数を含む方程式を考えてみましょう。\ \frac{1}{4}x\frac{1}{2}=\dfrac{1}{4}x\dfrac{3}{2} \これも、分数のまま計算することもできます。しかし、小数のときよりもさらに計算が面倒になりそうですね。方程式は両辺に同じ数を掛けてもいいので、分数が残らない形にし. 分数を含む方程式の手順0 分数を消すために両辺に分母の最小公倍数をかける。 問題 次の方程式を解きなさい。 方程式に分数が含まれている場合、分母の最小公倍数(通分する数)を両辺にかけて分数を消してやります。 今回は分母の数が3と4なので最小公倍数である12を両辺にかけます。 そうすると両辺から分数が消えました。 これが分数が含まれている方程式の手順0ですね。 以下は手. 分数を含む一次方程式の練習問題です。 解説記事はこちら gt;一次方程式の解き方を解説!かっこや分数の場合のやり方も! スポンサーリンク 目次1 方程式練習問題分数を含む一次方程式2 練習問題の解答&解説21 M.
例題次の二次方程式を解け。 小数は両辺を10倍、100倍して小数を消しましょう。 分数を含む二次方程式 例題次の二次方程式を解け。 分数が出てきたときには、 分母の最小公倍数を両辺に掛けて、分数を消すようにしましょう。 分子が多項式になっている場合には、かっこをつけることも忘れないように! 練習問題次の二次方程式を解きなさい。 (1) (2) (3) 解説&答えはこち. 微分方程式とは、 ある関数とその導関数を含む方程式 のことです。 つまり、 の関数 とその導関数 ( )を含んだ式は微分方程式といえます。 この方程式を満たす 関数 がこの方程式の解 であり、これを求めることを「微分方程式を解く」といいます。 微分方程式の解(一般解と特殊解) 微分方程式の解には、「一般解」と「特殊解」の 種類があります。 一般解 任意定数を含む解。 微. 応用: 分数式を含む方程式や不等式を解く際に,分数式の通分が必要になる場合が多いです。 →分数不等式のおすすめの解き方と例題 分数式の足し算と引き算(分母が異なる場合) 分母が異なる分数式の足し算は, 通分してから分子を足し算 です: 例 x x 2 3 x 3 = x (x.
次の方程式を解きなさい.(分数は既約分数それ以上約分できない形で答えなさい.) 問題 解答 評価 (1) = 両辺の分子に10を掛けると = 約分すると 5x=6 両辺を5で割ると x= x = (2) = 両辺の分子に 8x を掛けると = 約分すると 16=7x 左辺と右辺を入れかえると 7x=16 両辺を7で割ると x= x = (3) = 両. 一次不定方程式の解き方は、特殊解を見つけること。 これに尽きます。 解答 (1) x = 2 x = 2 , y = 1 y = 1 のとき成り立つ。 よって、 { 3 x − 5 y = 1 ① 3 ・ 2 − 5 ・ 1 = 1 ② { 3 x − 5 y = 1 ① 3 ・ 2 − 5 ・ 1 = 1 ② ① − ② ① − ② をすると 3 ( x − 2) = 5 ( y − 1) 3 ( x − 2) = 5 ( y − 1) となり、 3 3 と 5 5 は互いに素であるため、ある整数 k k を用いて x.
3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく

連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト

方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
分数 を 含む 方程式 解き方 のギャラリー

中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット

方程式 分数を含む方程式 中学生 数学のノート Clearnote

方程式と計算ノート セルモ大蔵 世田谷 の塾長ブログ

分数方程式 分数不等式 数学の偏差値を上げて合格を目指す
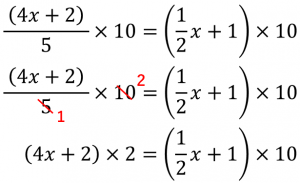
中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす

分数をふくむ連立方程式 Youtube
置き換えによる連立方程式 まなびの学園
3 3 方程式 かっこ 勉強できようサイト

一次方程式の解の求め方 数学fun

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

小数を含む方程式の計算の手順を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
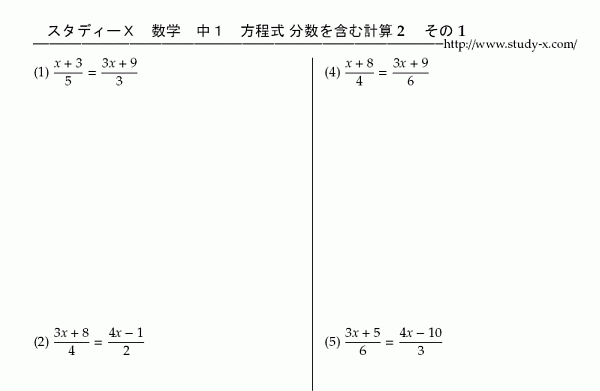
方程式 分数を含む方程式2 無料学習プリント教材

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく

分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

中1 方程式の解き方 分数はいる方程式 中学生 数学のノート Clearnote
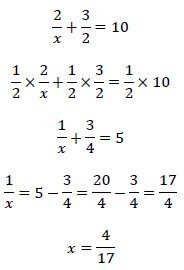
方程式とは 1分でわかる意味 移項 1次方程式の解き方と計算問題 分数の関係

係数に分数を含む1次方程式 Kyokuryo Math
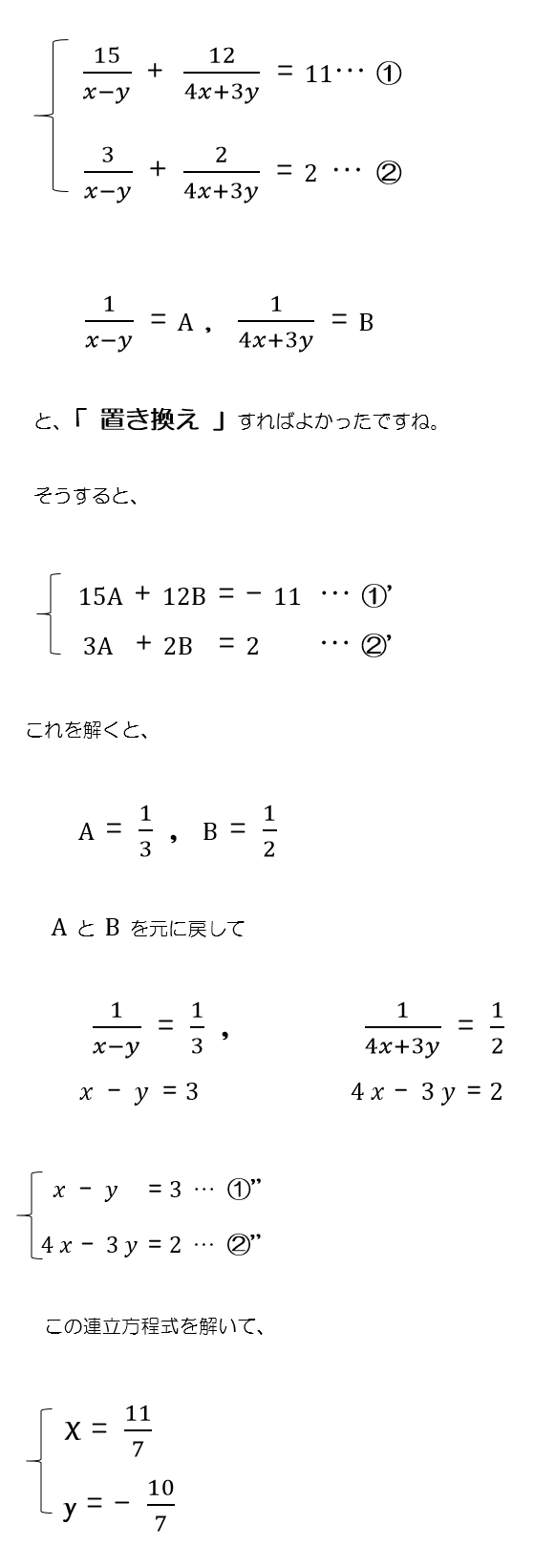
なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬

1次方程式の解き方 その3 算数 数学が好きになりmath

中1 1次方程式 でつまずく原因と解決法 分数
1

中学1年生 数学 無料問題集 分数の一次方程式 おかわりドリル
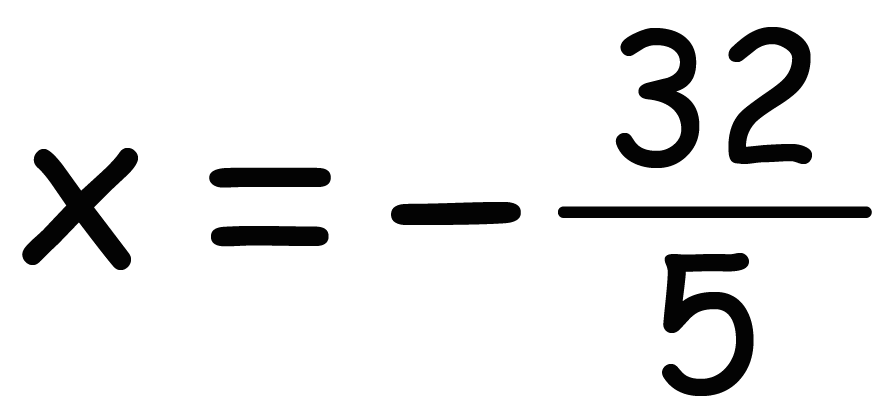
中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく

分数を含む方程式 Youtube
3

1次方程式の解き方はルールを覚えれば簡単 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ

中学1年生 数学 無料問題集 分数を含む比例式と一次方程式 おかわりドリル

思考を見せる板書例 1年3章 係数を含む方程式の解き方 Math Connect 東京書籍 先生のための算数数学ポータルサイト

中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット

数学のヘルプ 数学方程式を理解する

1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト

連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト

分数を含む方程式 中1数学 方程式7 Youtube

分数を含む方程式の解き方がわかりません 教えてください Clear

中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ
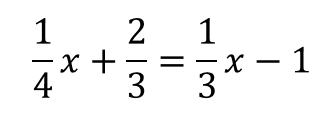
中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ
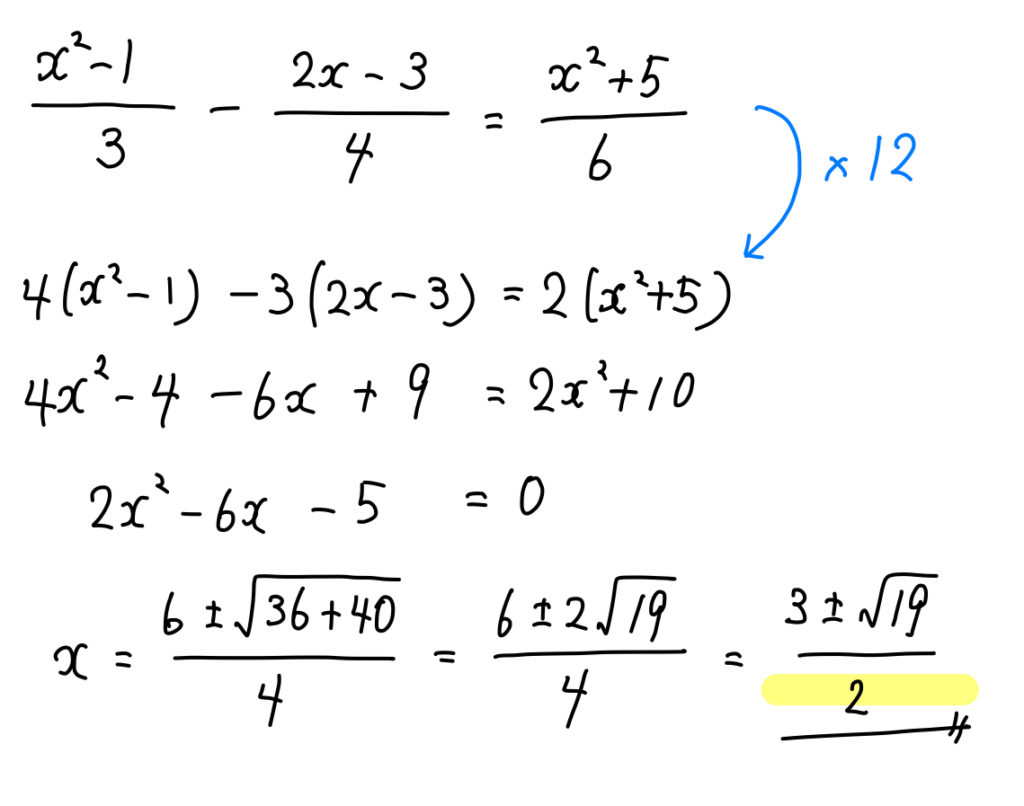
分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ

中1数学 方程式 2 4 分数を含む1次方程式 Youtube

方程式 分数を含む方程式 中学生 数学のノート Clearnote

中1 1次方程式 でつまずく原因と解決法 分数

連立方程式の解き方 係数に分数がふくまれる場合 Youtube

Junior High数学的 中1 数学 方程式の解き方 筆記 Clearnote

中学1年 方程式の解き方 第7講 清水塾

中学数学 連立方程式 の効果的な教え方 小数 分数問題

中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく
連立方程式の小数と分数の混ざった式について この問題が解 Yahoo 知恵袋

複雑なルートの分数の有理化のやり方と問題 理系ラボ

中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ
中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
方程式 分母にxがあるときの解き方は 数スタ
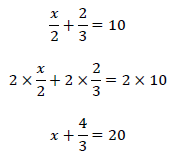
方程式とは 1分でわかる意味 移項 1次方程式の解き方と計算問題 分数の関係
連立方程式

中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

中1 1次方程式 でつまずく原因と解決法 分数
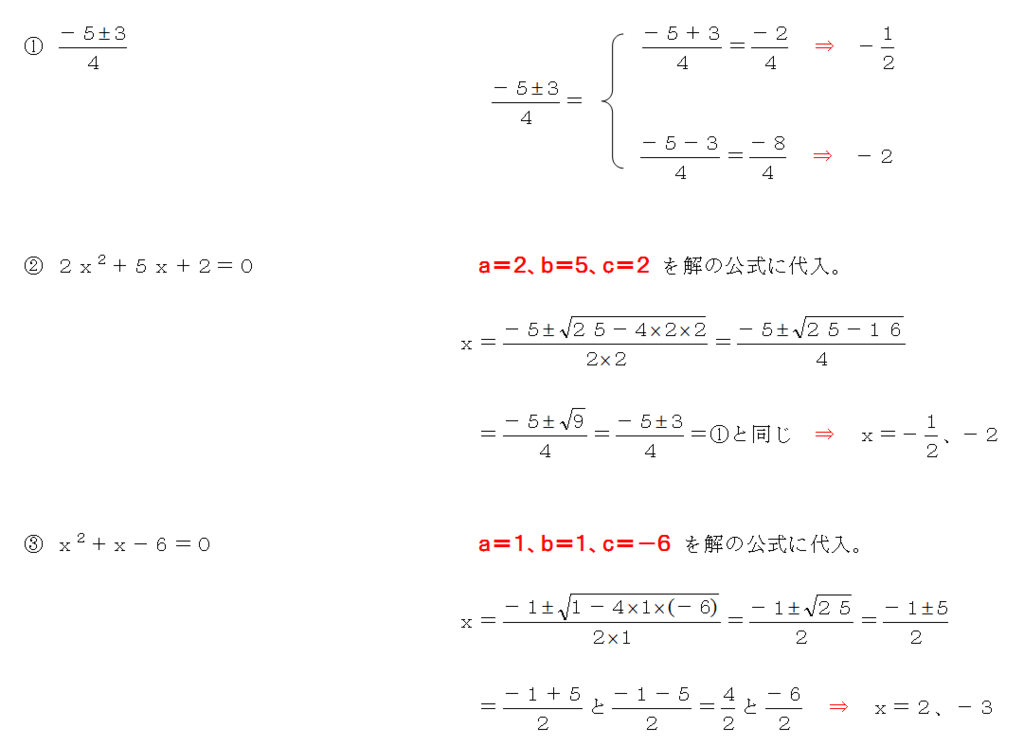
解の公式を使う問題 答えがルートにならないパターン 中学や高校の数学の計算問題

一次方程式 分数があるパターン Youtube

中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

分数を含む方程式の計算の手順を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに

中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
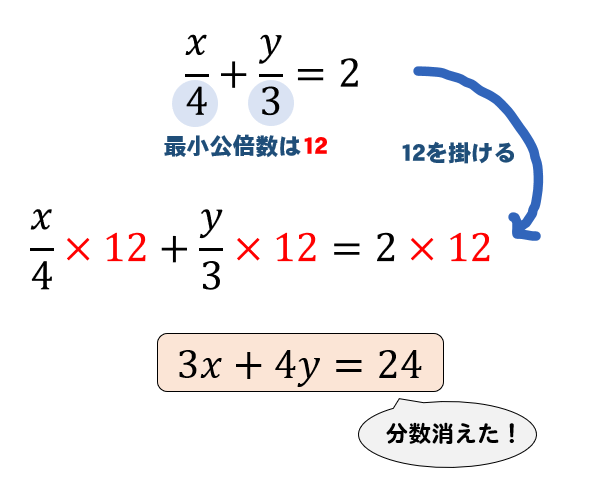
連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト
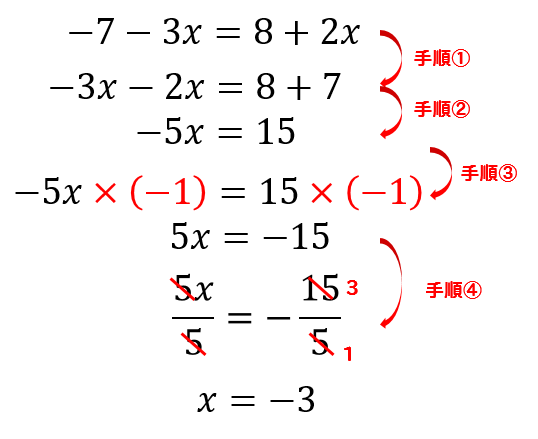
中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

分母の数が大きい場合の計算 連立方程式 中学生からの勉強質問 数学 進研ゼミ中学講座

分母にxのある方程式の解き方を教えて頂けますか 分母にxのある方程 数学 教えて Goo

方程式 分母にxがあるときの解き方は 数スタ
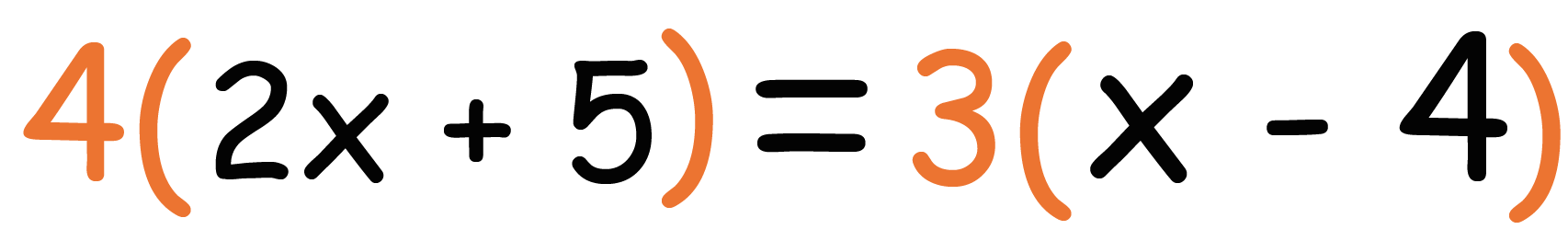
中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく

数学のヘルプ 数学方程式を理解する
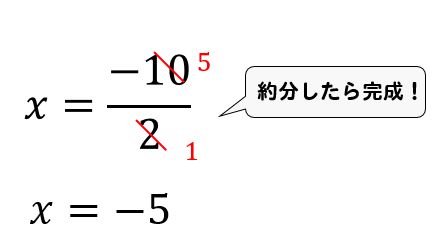
一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト

中1 数学 中1 30 方程式を解く 小数と分数編 Youtube

中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ
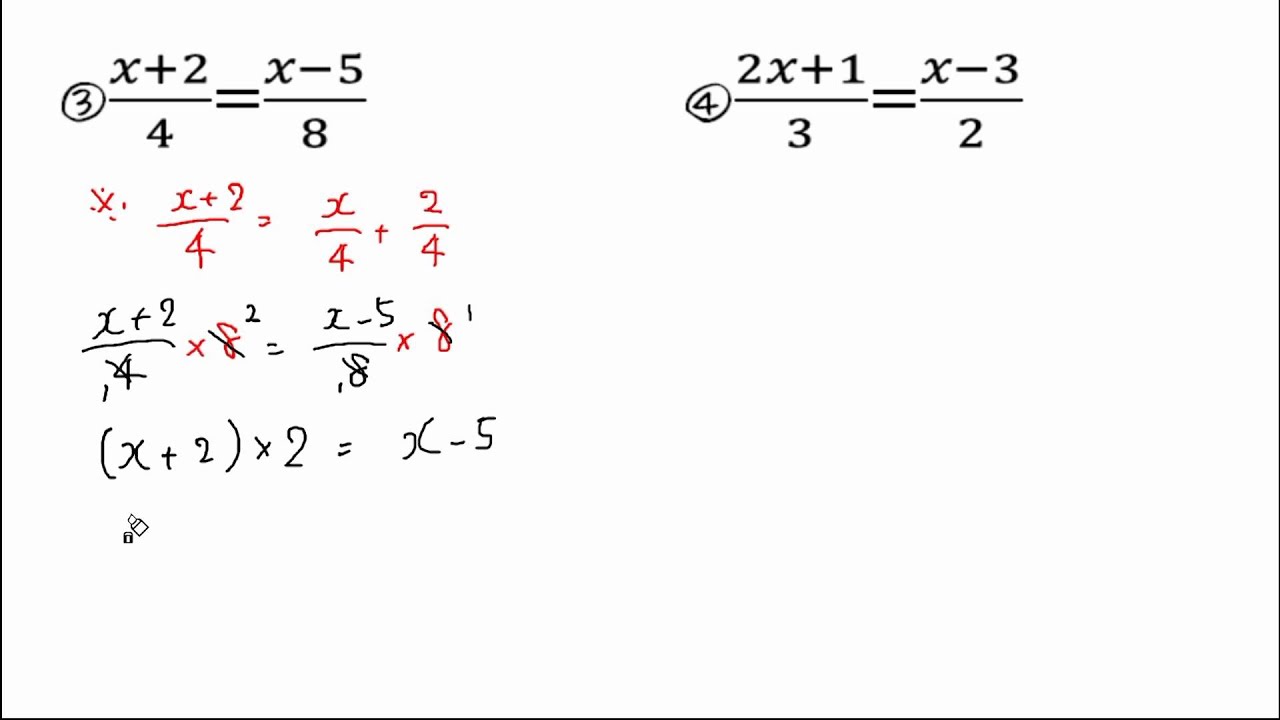
分数の入った方程式 問題 Youtube

中学数学1年 いろいろな1次方程式 かっこを含む 係数が小数 係数が分数 受験の月
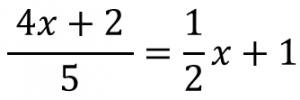
中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす
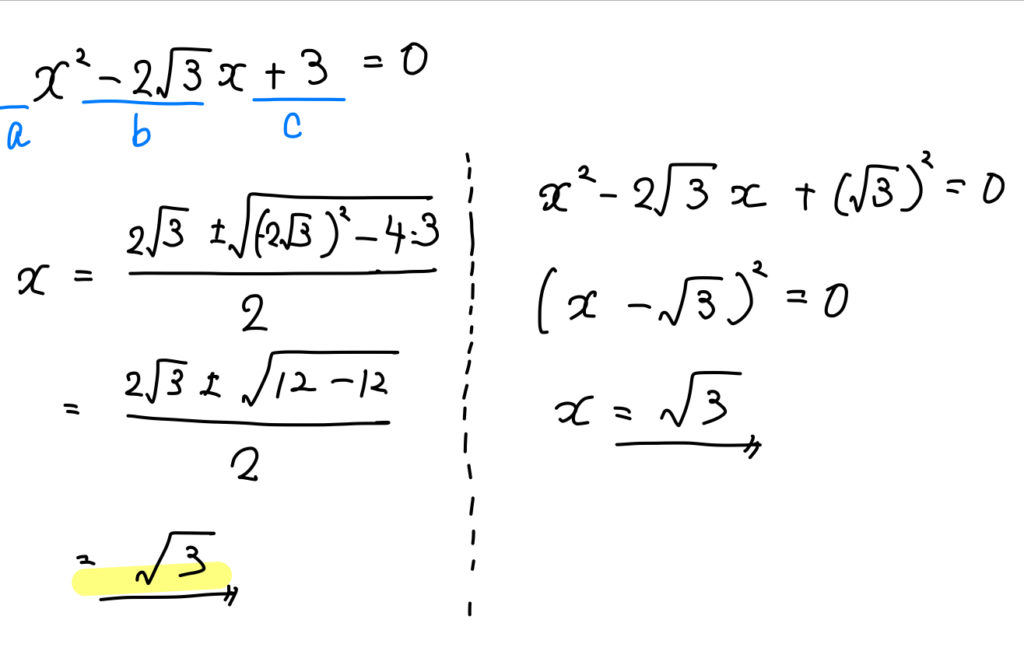
分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ

中1数学 分数を含む方程式の解き方 Youtube
中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
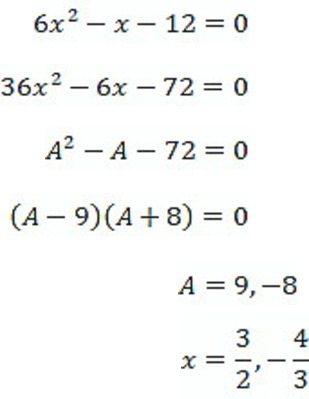
2次方程式の解法のオリジナル技 少しマニアック 公式 学習塾 志學舎

高校数学 様々な2次方程式の解法 分数 小数 根号 置換 絶対値 受験の月
Kishiki J Kishiwada Ed Jp

分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題

中1数学 方程式の解き方4 カッコ 分数 小数 例題編 映像授業のtry It トライイット

中1 中1 かっこ 分数 小数のある方程式 中学生 数学のノート Clearnote
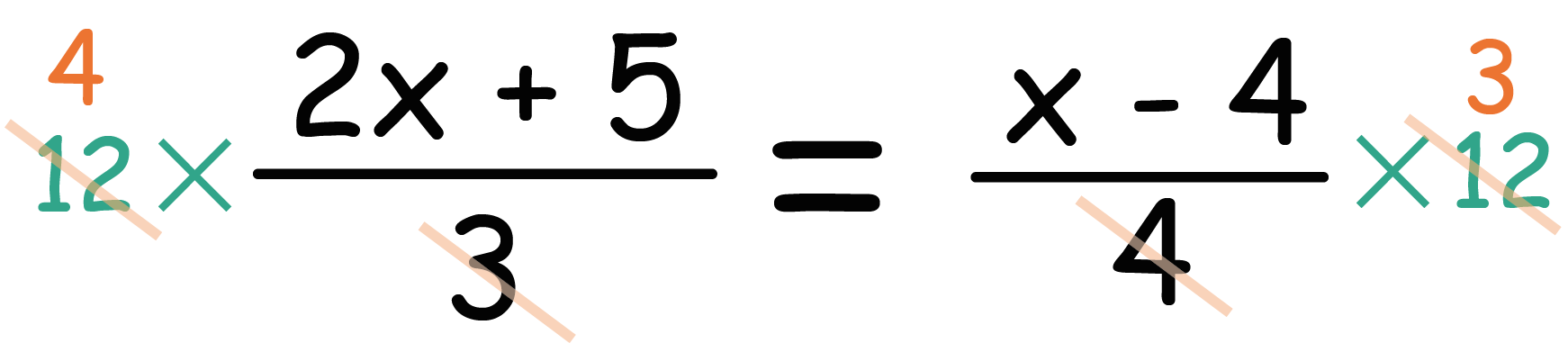
中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく
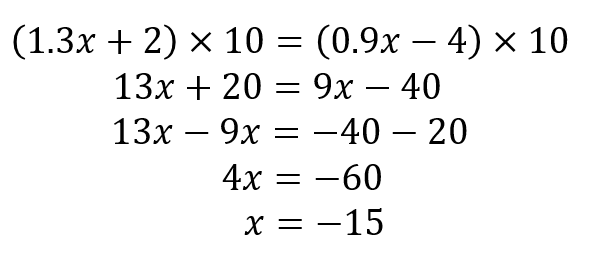
中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ
高2です指数方程式分数になると分かりませんどなたか教えてください Yahoo 知恵袋

中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく
一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト

画像の 3 のような分数と小数の混ざった連立方程式がわかりません 解 数学 教えて Goo
1

絶対値記号を含む方程式 不等式の解き方 数学 苦手解決q A 進研ゼミ高校講座

中1方程式 分数が含まれるときの解き方を問題解説 Youtube

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく
最も欲しかった 分数 を 含む 方程式 解き方 Josspix03tr
高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト
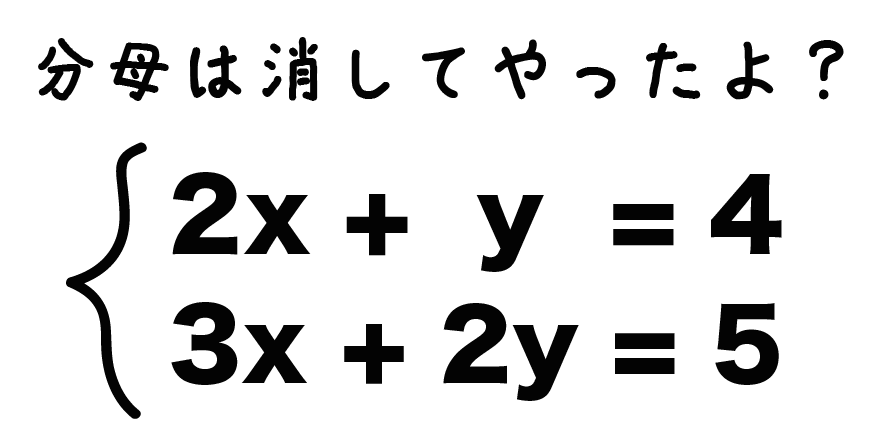
3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




