Cylinder X2+y24
The way the two cylinders and the quadrant planes cut each other, the shape in the xzplane is a 2x2 square, the shapes in the xy and yz planes are each quarter circles of radius 2 Their intersection is a quarter section of a 2 x 28 ellipse It is made of two mirrorimaged sections cut by the quarter ellipse.

Cylinder x2+y24. Double Integrals in polar coordinates setup #1 r_swayze 66 0 Use polar coordinates to find the volume of the given solid inside the sphere x^2 y^2 z^2 = 16 and outside the cylinder x^2 y^2 = 4. See the explanantion This is the equation of a circle with its centre at the origin Think of the axis as the sides of a triangle with the Hypotenuse being the line from the centre to the point on the circle By using Pythagoras you would end up with the equation given where the 4 is in fact r^2 To obtain the plot points manipulate the equation as below Given" "x^2y^2=r^2" ">". X ^2 y ^2 = 4 and x ^ 2 z ^ 2 = 4?.
Cylinder x 2y = 4, oriented with normals pointing upward, and G~is the vector eld G~(x;y;z) = h 1;. 148 Lagrange Multipliers 148 Lagrange Multipliers Many applied max/min problems take the form of the last two examples we want to find an extreme value of a function, like V = x y z, subject to a constraint, like 1 = x 2 y 2 z 2 Often this can be done, as we have, by explicitly combining the equations and then finding critical points. Show Solution Okay, since we are looking for the portion of the plane that lies in front of the y z y z plane we are going to need to write the equation of the surface in the form x = g ( y, z) x = g ( y, z) This is easy enough to do x = 1 − y − z x = 1 − y − z Next, we need to determine just what D D is.
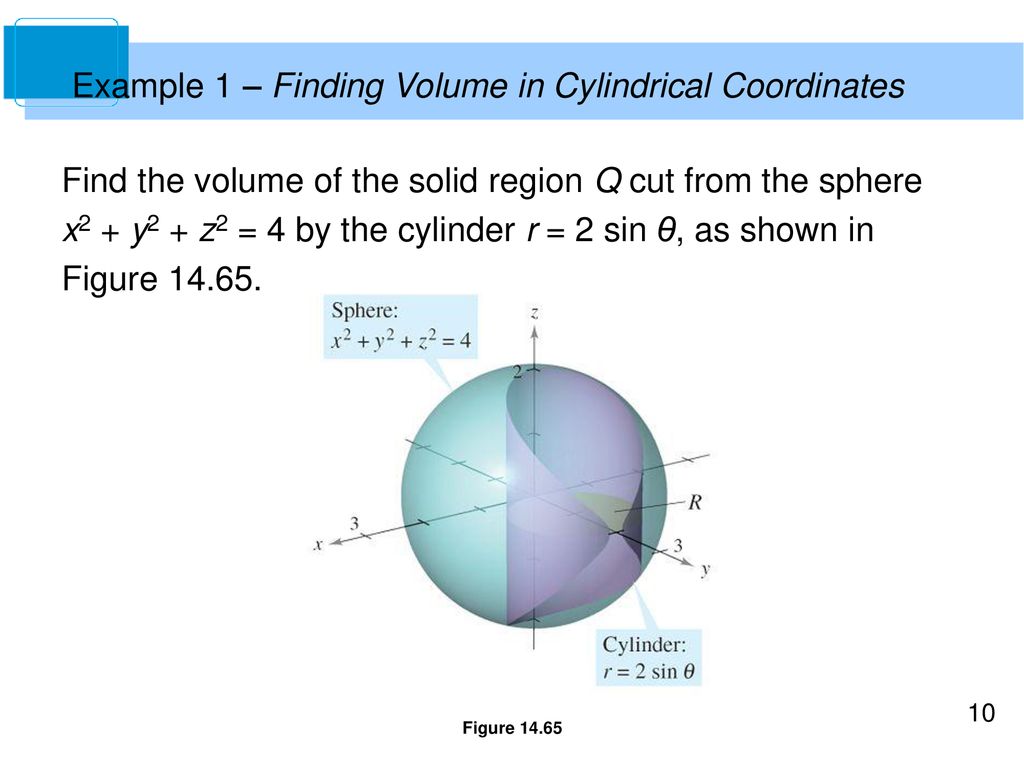
F(x, y, z) = –y2 i x j z2 k C is the curve of intersection of the plane y z = 2 and the cylinder x2 2 y = 1 (Orient C to be counterclockwise when viewed from above) could be evaluated directly, however, it’s easier to use Stokes’ Theorem C ∫Fr⋅d Example 1 C ∫Fr⋅d. ExampleFind the volume of the portion of the sphere x2y2z2 = 4 inside the cylinder (y − 1)2 x2 = 1 Figure 6 Soln The topsurface isz = p 4−x2 − y2 = √ 4−r2 andthebottomis z = − p 4−x2 − y2 = − √ 4− r2 over the region D defined by the cylinder equation in the xyplane So rewrite the cylinder equation x2 (y −1)2 = 1 as x2 y2 −2y 1 = 1 ⇒ r2 = 2rsin(θ) ⇒ r = 2sin(θ) V(E) = ZZZ. (c) the part of the hyperbolic paraboloid z = y 2− x2 that lies between the cylinders x y2 = 1 and x 2 y = 4 Answer Here D lies between circles of radii 1 and 2 with centers at the origin 0 ≤ θ ≤ 2π,.
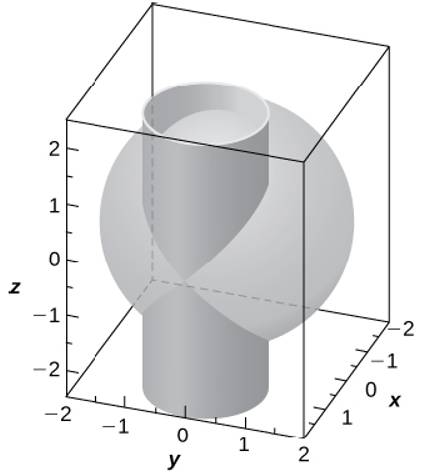
Find the volume of the solid that lies within both the cylinder x 2 y 2 = 1 and the sphere x 2 y 2 z 2 = 4 I decided to use polar coordinates so that the cylinder equation becomes r 2 = 1 and the sphere becomes r 2 z 2 = 4 Solving for z, I get the inequality − 4 − r 2 ≤ z ≤ 4 − r 2 Since I know what r 2 is, I plug that in to get the inequality where z is between − 3. Use traces to sketch the surface z = 4x2 y2 Solution If we put x = 0, we get z = y2, so the yzplane intersects the surface in a parabola If we put x = k (a constant), we get z = y2 4k2 This means that if we slice the graph with any plane parallel to the yzplane, we obtain a parabola that opens upward Similarly, if y = k, 2the trace is z = 4x k2, which is again a parabola that opens. Cylinder x2 y2 = 4, oriented clockwise when viewed from above Solution Let S be the part of the plane 3x 2y z = 6 that lies inside the cylinder x 2 y 2 = 1, oriented downward.
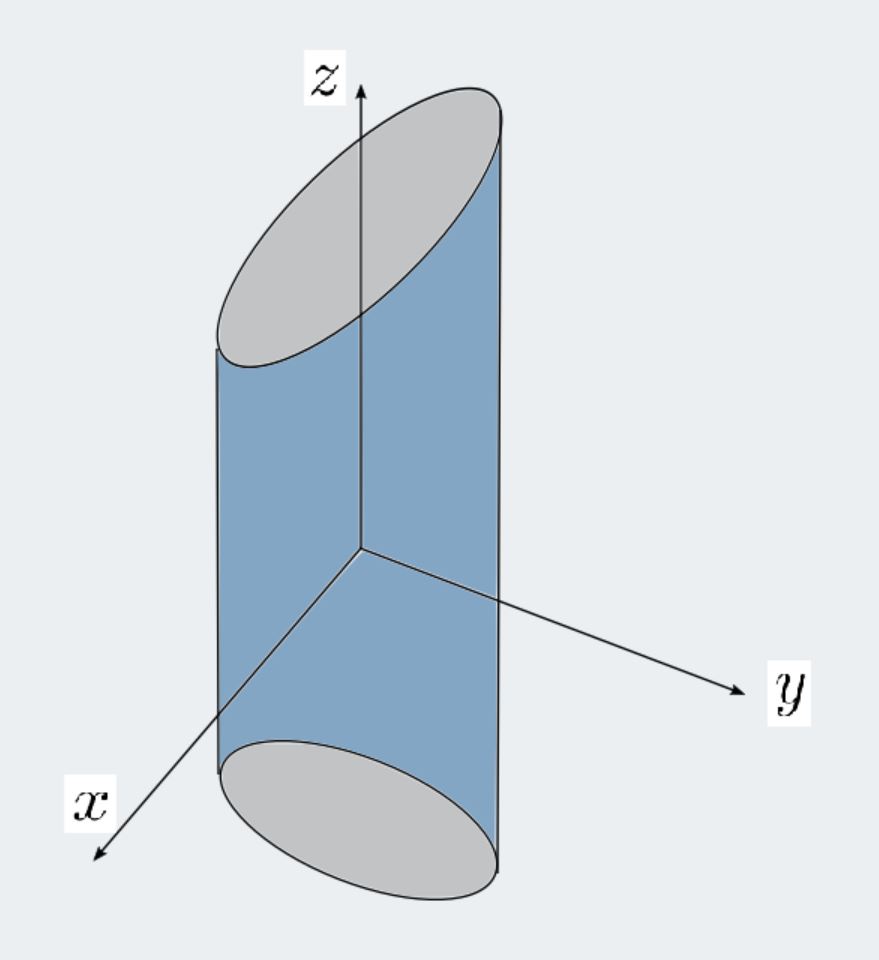
In the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tube. Of a curved wedge cut out from a cylinder (x − 2)2 y2 = 4 by the planes z = 0 and z = −y Solution First sketch the integration region I (x − 2)2 y2 = 4 is a circle in the xyplane, since x2 y2 = 4x ⇔ r2 = 4r cos(θ) r = 4cos(θ) I Since 0 6 z 6 −y, the integration region is on the y 6 0 part of the z = 0 plane y z = y 2 4 z x (x 2) y = 42 2. Inside the sphere x 2 y 2 z 2 = 25 and outside the cylinder x 2 y 2 = 9 Expert Answer Who are the experts?.
(b) F(x,y,z) = (x 2 sin(yz))i (y − xe−z)j z k;. YdS, where Sis the part of the paraboloid y= x 2 z2 inside the cylinder x2 z = 4 We already have yas a function of the other two variables, and we want to use xand zas parameters The projection of Sonto the xzplane is the disk D= f(x;z) x 2 z 2 4g. Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 100% (12.
S is the surface of the region bounded by the cylinder x2 y2 = 4 and the planes x z = 2 and z = 0 Solution The divergence of F is divF = ∂ ∂x (x2 sin(yz)) ∂ ∂y (y − xe−z) ∂ ∂z (z2) = 2x 12z Let E. 2 The part of the surface x−y z = 4 that is within the cylinder x2 y2 = 9 3 The part of the surface z = x2 y2 that is above the region in the xyplane given by 0 ≤ x ≤ 1, 0 ≤ y ≤ x2 4 The part of the paraboloid y = 9−x2 −z2 that is on the positive y side of the xzplane 5. And bounded on the sides by the cylinder x2 y2 x = 0 Solution V = Zˇ=2 ˇ=2 Zcos 0 (1 r2)rdrd = Zˇ=2 Find the surface area of the paraboloid z = 4 x2 y2 that lies above the xyplane Solution For this problem polar coordinates are useful S = ZZ D s 1 @z @x 2 @z @y 2 dA = ZZ D p.
Answer (1 of 2) Before I answer your question I will just like to give brief idea about how the equation of the cylinder is driven A cylinder is a surface generated by a straight line which is parallel to a fixed line and intersects a given curve or touches a given surface The fixed line is c. And y = 2sint The value of the zcoordinate of a point on the cylinder represents the height h of that point So, the cylinder can be parametrized as x= 2cost;. See the answer See the answer See the answer done loading Use polar coordinates to find the volume of the given solid Inside the sphere X 2 y 2 z 2 =16 and outside the cylinder X 2 y 2 =4 I do not understand why you have to multiply to integrand by two in order to obtain the volume of the solid Thanks!.
I am given the plane $x y z = 1$ and the cylinder $x^2 y^2 = 4,$ and have to find the surface area of portion of the plane that is inside the cylinder. Now, if we substitute the equation for the cylinder into this equation we can find the value of \(z\) where the sphere and the cylinder intersect \\begin{align*}{x^2} {y^2} {z^2} & = 16\\ 12 {z^2} & = 16\\ {z^2} & = 4\hspace{05in} \Rightarrow \hspace{025in}z = \pm. Paraboloid z =x2y2 and the plane z =4 x y z z =x2y2 It follows that the volume is given by V = ˆ 2π 0 ˆ 2 0 ˆ 4 x2y2 dzrdrdθ =2π ˆ 2 0 ˆ 4 x2y2 dzrdr =2π ˆ 2 0 (4−x2−y2)rdr =2π ˆ 2 0 (4−r2)rdr = =8π Notice also that this solid can be recognized as a solid of revolution In.
154 Surface Integrals 573 44 Show that the spin field S does work around every simple inside R can be squeezed to a point without leaving R Test closed curve these regions 1 xy plane without (0,O) 2 xyz space without (0, 0,O) 45 For F =f(x)j and R = unit square 0. 2(7 points) Express the volume of the solid that lies within both the cylinder x2 y2 = 1 and the sphere x 2 y z2 = 4 as an integral using cylindrical coordinates and evaluate it Solution The sphere can be expressed as z= p 4 x 2 y2 = 4 r So the volume can be expressed in cylindrical coordinates as V = ZZZ 1 dV = Z 2ˇ 0 Z 1 0 Zp 4 r2 p. Where S is the part of the sphere x2 y2 z2 = 4 that lies inside the cylinder x2 y2 = 1 and above the xyplane See the figure below Strategy Use a two step process Step 1 Express f (x,y,z) in terms of the independent variables (in this case) x and y So in this example f (x,y,z) = y2 Step 2 Write the surface area element, dS in terms of dA dS = N dA.
Cylinder z = (4−y2)1/2 below by the xy plane and the projection D of the solid onto the xyplane is the triangle with edges x = 2y, x = 0 and the intersection of the cylinder with the plane z = 0 which gives y2 = 4 or y = 2 (first octant) The volume is ZZ D (4−y2)1/2dA = Z 2 0 Z 2y 0 (4−y 2)1/ dxdy = Z 2 0 2y(4−y2)1/2dy = − 2 3 (4−y2)3/22 0 = 16 3 6. Since the sphere is x 2 y 2 z 2 = 4, x 2 y 2 z 2 = 4, which is r 2 z 2 = 4, r 2 z 2 = 4, and the cylinder is x 2 y 2 = 1, x 2 y 2 = 1, which is r 2 = 1, r 2 = 1, we have 1 z 2 = 4, 1 z 2 = 4, that is, z 2 = 3 z 2 = 3 Thus we have two regions, since the sphere and the cylinder intersect at (1, 3) (1, 3) in the r z r zplane. 9 Set up the integral to find the volume of the solid bounded above by the plane y z = 1, below by the xyplane, and on the sides by y=xand x = 4 a dzdxdy 0 1−y ∫ y2 2 ∫ 0 1 ∫ b dzdydx 0 1−y ∫ 0 x ∫ 0 1 ∫ c dzdydx 0 1−y ∫ x 2 ∫.
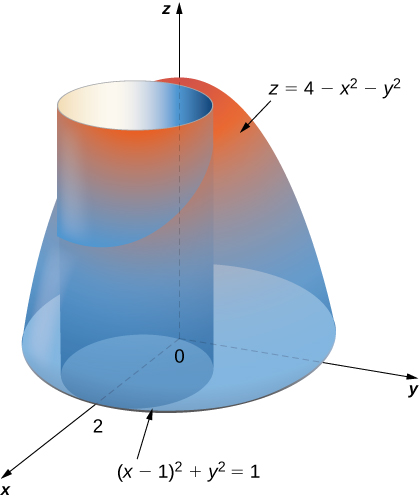
The cylinder x2 y2 = 4 and the surface z = xy Solution We can parameterize the cylinder x2 y2 = 9 by (3cos(t),3sin(t),z) Now x = 3cos(t) and y = 3sin(t) So z = xy = 3cos(t) 3sin(t) = 9cos(t)sin(t) So the intersection of the cylinder x 2 y = 9 and the surface z = xy can be represented by (3cos(t),3sin(t),9cos(t)sin(t)). Find the mass of the solid represented by the region in space bounded by z = 0, z = 4x 2y 2 3 and the cylinder x 2 y 2 = 4 (as shown in Figure 1473), with density function δ (x, y, z) = x 2 y 2 z 1, using a triple integral in cylindrical coordinates. In this video explaining triple integration exampleFirst set the limits and after integrate This is very simple and good example#easymathseasytricks #defi.
Math 9 Assignment 11 — Solutions 2 where V = πa2b/4 is the volume of D, and ¯y = b/2 is the ycoordinate of the centroid of DThe final result is ZZ S → F ·→n dS = ZZ Stot F →n tot dS − πa2b2 4 = 2V 2Vy¯− 2 b2 4 = 2 2 3 Using the divergence theorem, evaluate. Find stepbystep Calculus solutions and your answer to the following textbook question Bounded by the cylinder x^2y^2=1 and the planes y=z, x=0, z=0 in the first octant. Calculus Calculus questions and answers Write an integral that would calculate the volume of the bounded solid by the cylinder x^2 y^2 =4 and the plans of yz=4 , y=0 y>0.
Z= h using the angle tand the height has two parameters. 4 Evaluate RRR H e p x 2y z dV, where His enclosed by sphere x2 y2 z2 = 9 in the rst octant Solution In spherical coordinates it becomes R ˇ=2 0 R ˇ=2 0 R 3 eˆˆ2 sin˚dˆd˚d = (ˇ=2)(5e3 2) 5 Find the volume of the solid that lies within the sphere x 2 y2 z = 4, above the xyplane and below the cone z= p x2 y2. X 2y z2 =16 and outside the cylinder x 2y =4 Solution This volume is given by 2 ZZ D p 16−x2 −y2 dA where D is the domain D = © (x,y) 4 ≤x2 y2 ≤16 ª Using polar coordinates, we see that the volume is 2 Z 2π 0 Z 4 2 √ 16−r2rdrdθ=32 √ 3π 4.
The cylinder x^2y^2=4 and the surface z=xy Efan Halliday Answered Find a vector function that represents the curve of intersection of the two surfaces The cylinder \(x^2y^2=4\) and the surface z=xy 2 See Answers. • The cylinder x 2 y = 4 is based on the circle x = 2cost;. Above and below by the sphere x2 y2 z2 = 9 and inside the cylinder x2 y2 = 4 z y x Page 5 of 18.
2i To do this new problem, let’s follow the same three steps we used in #4(a) on the worksheet \Flux Integrals" First, we parameterize S Since the plane has equation z= x4, we can use xand yas our parameters. Surfaces and Contour Plots Part 4 Graphs of Functions of Two Variables The graph of a function z = f(x,y) is also the graph of an equation in three variables and is therefore a surfaceSince each pair (x,y) in the domain determines a unique value of z, the graph of a function must satisfy the "vertical line test" already familiar from singlevariable calculus. Use a CAS integration utility to evaluate the triple integral of the given function over the specified solid region F(x, y, z) = 2 (x2 y2 z2)3 / 2 over the solid bounded below by the cone z = √x2 y2 and above by the plane z = 1 Check back soon!.
X2 dV , where E is the solid that lies within the cylinder x 2 y2 = 1, above the plane z = 0, and below the cone z2 = 4x 4y2 Solution In cylindrical coordinates the region E is described by 0 ≤ r ≤ 1, 0 ≤ θ ≤ 2π, and 0 ≤ z ≤ 2r Thus, ZZZ E. Find stepbystep Calculus solutions and your answer to the following textbook question Use polar coordinates to find the volume of the given solid Inside the sphere x^2y^2z^2=16 and outside the cylinder x^2y^2=1. Explanation Cylindrical Volume V = ∫V r dr dz dθ = ∫ 2π θ=0∫ 2 r=0∫ 4−rsinθ z=0 r dz dr dθ = ∫ 2π θ=0∫ 2 r=0 (rz)4−rsinθ z=0 dr dθ = ∫ 2π θ=0∫ 2 r=0 4r − r2sinθ dr dθ = ∫ 2π θ=0( 2r2 − r3 3 sinθ)2 r=0 dθ.
Example 1762 An object occupies the space inside both the cylinder x 2 y 2 = 1 and the sphere x 2 y 2 z 2 = 4, and has density x 2 at ( x, y, z) Find the total mass Spherical coordinates are somewhat more difficult to understand The small volume we want will be defined by Δ ρ, Δ ϕ , and Δ θ, as pictured in figure 1761.
Ocw Mit Edu
Parker Com

What Is The Formula Of A Parabolic Cylinder Opening Upward From A
Cylinder X2+y24 のギャラリー
Find The Volume Bounded By The Paraboloid 𝒙𝟐 𝒚𝟐 𝒂𝒛 And The Cylinder 𝒙𝟐 𝒚𝟐 𝒂𝟐 Applied Mathematics 2 Shaalaa Com
12 6 Quadric Surfaces Mathematics Libretexts

Let S Be The Surface Of The Solid Bounded By The Cylin Itprospt

Solved A Solid E Lies Within The Cylinder X 2 Y 2 9 Chegg Com

Z 0 0 2 1 1 2 2 And 1 3 3 Find The Volume Of The Solid That Is Homeworklib

Cone In Cylindrical Coordinates

Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5
Mathweb Math Ncu Edu Tw

Solved Find The Area Of The Surface The Part Of The Cylinder X 2 Z 2 4 That Lies Above The Square With Vertices 0 0 1 0 0 1 And 1 1
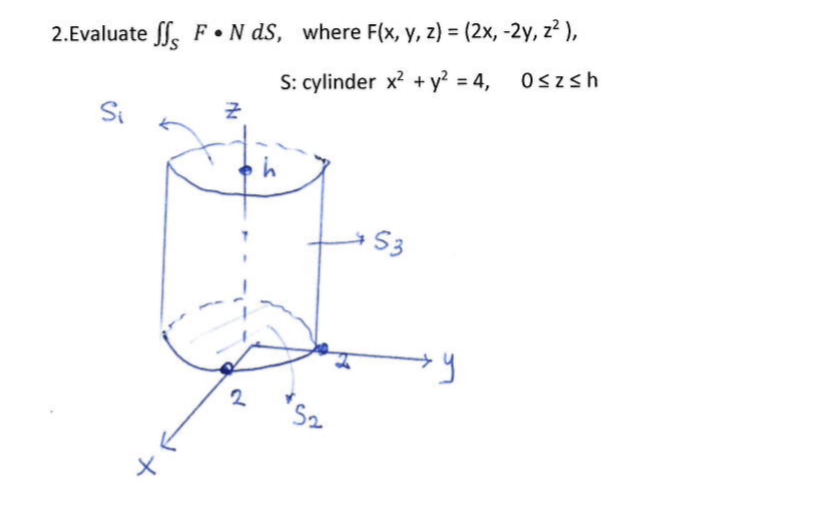
Solved Where F X Y Z 2x 2y 22 S Cylinder X2 Y2 Chegg Com
Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3
Create Cylinder Matlab Cylinder

2 Bore X 4 Stroke Hydraulic Cylinder Welded Cross Tube Double Acting Cylinder Magister Hydraulics

2 Bore X 4 Stroke Hydraulic Cylinder Welded Cross Tube Double Acting Cylinder Magister Hydraulics

Btech Ii Engineering Mathematics Unit3

Section 12 6 Triple Integrals In Cylindrical Coordinates Ppt Download

Triple Integrals In Cylindrical Coordinates Page 2

French Railways Smiiiiiiiiiihrtfiiiiiifa 2 4 2 Engine P O Type Of Boiler Flaman Composed Of Two Barrels The Lower One Completely Filled With Tubes Andthe Smaller Upper One For A Steam Space Theparis Orleans Engines

Find The Volume Inside Both The Cylinder X 2 Y 2 1 And The Sphere X 2 Y 2 Z 2 4 Study Com

Lego Cylinder Half 2x4x5 With 1x2 Cutout For Sale Online Ebay

3d Integration Cylindrical Coord

Math Help

Find A Vector Function That Represents The Curve Of Intersection Of The Two Surfaces The Plainmath
Hartleymath Triple Integrals
Solved Use Cylindrical Coordinates Find The Volume Of The Solid That Lies Within Both The Cylinder X 2 Y 2 1 And The Sphere X 2 Y 2 Z 2 4

Solved Problems To Evaluate The Double Integrals Homework 9 M 427l Docsity

Mathematics Calculus Iii

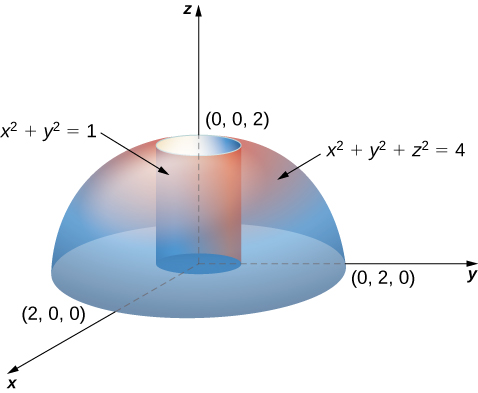
Region D Is Bounded By Below By Z 0 And Above By X 2 Y 2 Z 2 4 And On Sides X 2 Y 2 1 Is Required To Be Setup In Spherical Coordinate Mathematics Stack Exchange

A Solid Is Bounded By The Paraboloid Z X 2 Y 2 The Cylinder X 2 Y 2 4 And The Xy Plane Use Cylindrical Coordinates To Find Its Volume And Its Centroid Study Com
Faculty Nps Edu
Ualberta Ca

Cylinder Hyd 4 In Bore X 2 In Stroke Hydraulic Cylinders Amazon Com Industrial Scientific
Uomustansiriyah Edu Iq
T The Intersection Between Cylinder X 1 2 Y 2 1 And Sphere X 2 Y 2 Z 2 4 Is Called

Taller Calculo B
Whitman Edu
Www3 Nd Edu

Find The Area Of The Surface The Part Of The Surface Z Xy That Lies Within The Cylinder X2 Y2 Brainly Com
Calculus Iii Surface Integrals

Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download
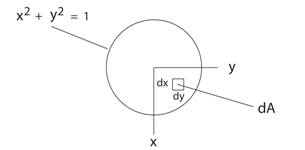
Math Help
Solved The Portion Of The Surface Z 6 Xy That Lies Within The Cylinder X 2 Y 2 3 Has A Surface Area Equal To Course Hero

Triple Integral Find Volume X 2 Cylinder X 2 Y 2 1 Above Z 0 Below Line Z 2 4 X 2 4 Y 2 Youtube

E9 Triple Integrals Ii College Algebra Math 17 University Of Studocu

Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5

Find The Volume Of The Solid In The First Octant Bounded By The Cylinders R 2 R 5 Z 8 X Y G Brainly Com

Find The Volumes Of The Regions The Region Cut From The Cylinder X 2 Y 2 4 Youtube

Find Correct To Four Decimal Places The Length Of The Curve Of Intersection Of Plainmath
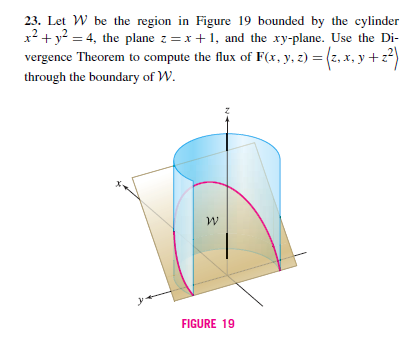
Solved Let W Be The Region In Figure 19 Bounded By The Chegg Com

Use Stokes Theorem To Evaluate C F Dr Where C Is Oriented Counterclockwise As Viewed From Above F X Y Z 3yi Xzj X Y K C Is The

How Do You Graph X 2 Y 2 4 Socratic

2 X 4 Tie Rod Hydraulic Cylinders Premium Supply
Ocw Mit Edu

Answered Find The Volume Of The Indicated Bartleby

Find The Volume Of The Bounded By The Cylinder X 2 Y 2 4 The Planes Y Z 4 Z 0 Youtube
Cis Umac Mo

15 5 Triple Integrals In Cylindrical And Spherical Coordinates Mathematics Libretexts
X 2 Y 2 1
Cylindrical Surfaces
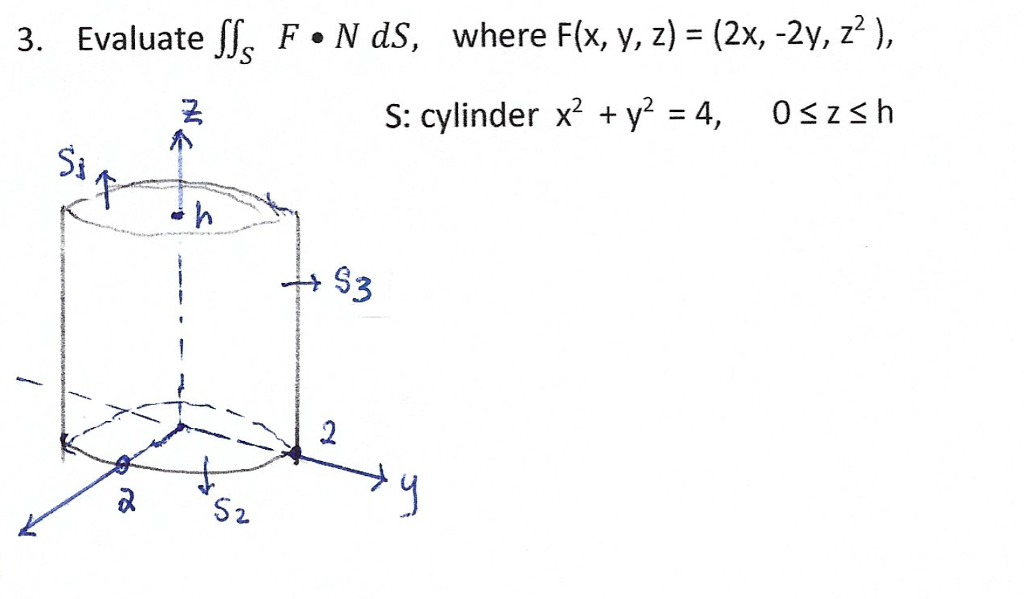
Solved Where F X Y Z 2x 2y S Cylinder X2 Y2 4 Chegg Com

Find The Volume Of The Solid In The First Octant Limit By X 2 Y 2 4 And Z Y 3 Mathematics Stack Exchange
How Am I Supposed To Visualise The Cylinder Math X 2 2 Y 2 4 Math In Three Dimensions X Y Z Quora
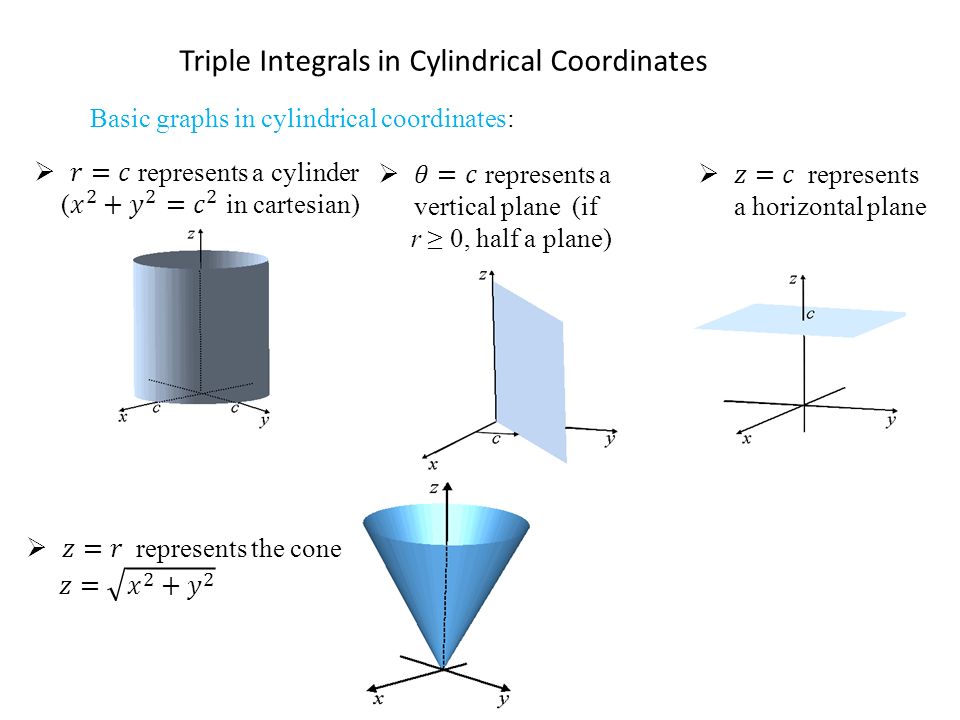
Triple Integral In Cylindrical Coordinates Ppt Video Online Download
X 2 Y 2 Z 2 1 In Spherical Coordinates Olsohaan
How To Find The Volume Of The Solid Region That Is Bounded By The Cylinders X 2 Y 2 1 And X 2 Z 2 4 Quora
Cylinder Equation 3d

Parametric Surfaces Pdf

15 Multiple Integrals Copyright Cengage Learning All Rights
Surface Area

Find The Volume Of The Solid Between The Cylinder X 2 Y 2 4 And The Sphere X 2 Y 2 Z 2 16 Study Com
Ppt Math23 Multivariable Calculus Powerpoint Presentation Free Download Id

Find The Volume Inside Both The Cylinder X 2 Y 2 4 And The Ellipsoid 4x 2 4y 2 Z 2 Youtube
Cylindrical Surfaces

Surface Integrals Ppt Download

Calc3 1001 By James Bardo Issuu

Cylinder Half 2 X 4 X 4

Intersection Of Two Cylinders
Double Integrals In Polar Coordinates Calculus Volume 3
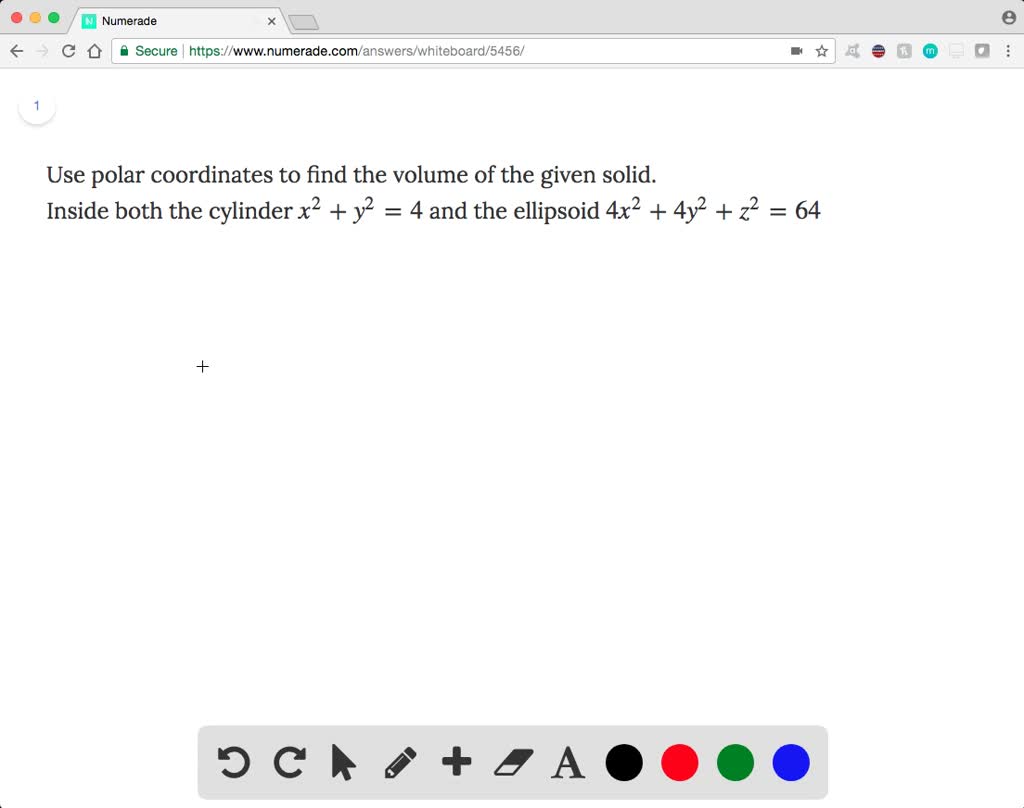
Solved Use Polar Coordinates To Find The Volume Of The Given Solid Inside Both The Cylinder X 2 Y 2 4 And The Ellipsoid 4x 2 4y 2 Z 2 64

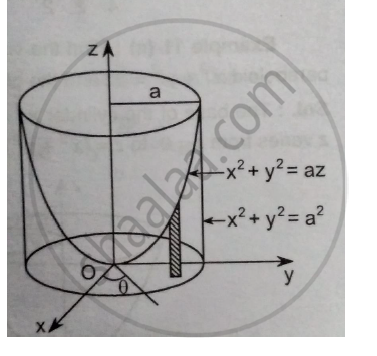
Find The Volume Bounded By The Parabolic X 2 Y 2 Az And The Cylinder X 2 Y 2 A 2
Surface Integral General Form Techniques And Examples

1 Point Find The Volume Of The Wedge Shaped Region Figure 1 Contained In The Cylinder X2 Y2 4 And Bounded Above By The Plane Z X And Below By The Xy Plane
Find The Volume Of The Paraboloid X 2 Y 2 4 Z Cut Off By The Plane 𝒛 𝟒 Applied Mathematics 2 Shaalaa Com
Ppt Math23 Multivariable Calculus Powerpoint Presentation Free Download Id

Solved A Solid E Lies Within The Cylinder X 2 Y 2 4 Chegg Com

Simple Geometry Question Equation Of Cylinder Mathematics Stack Exchange

Graph The Cylinder X 2 Y 2 16 And The Sphere X 2 Y 2 Z 2 49 Together Using Maple And Find The Volume Outside The Cylinder And Inside The Sphere Study Com
Math Diism Univpm It

Volumes

Math 263 Assignment 9 Solutions 1 Let F X Yz I Y Xz
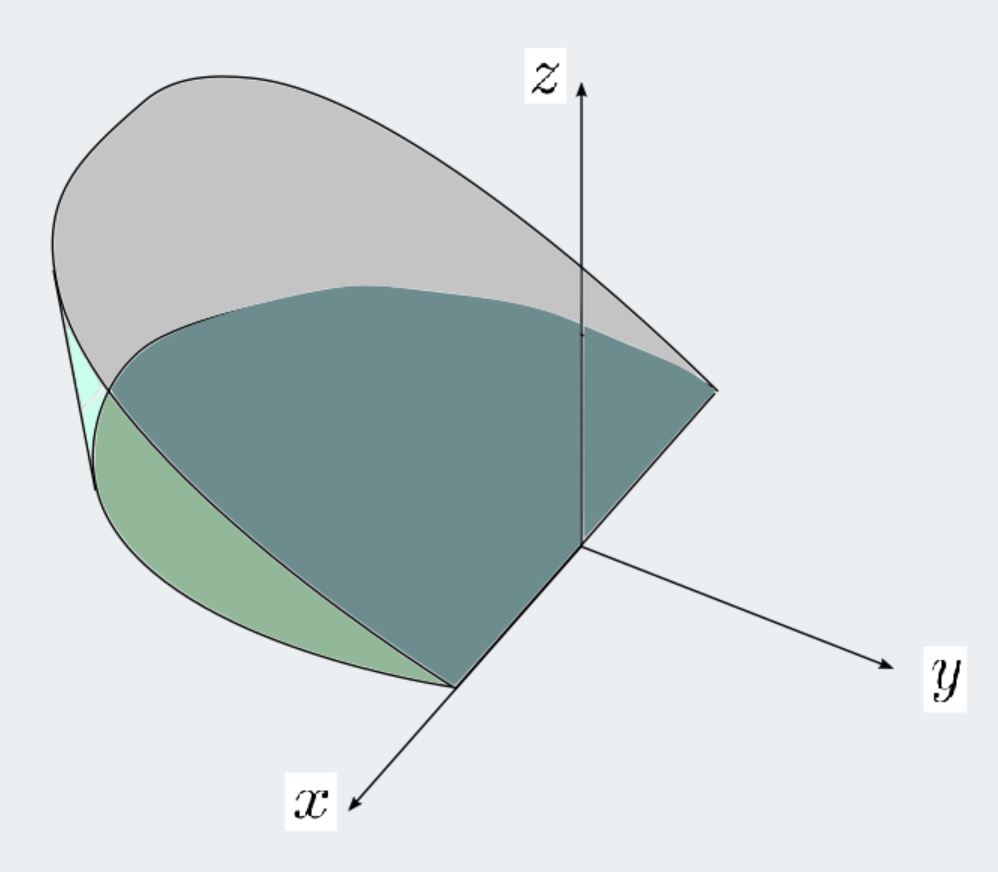
Hartleymath Triple Integrals
Mdpi Com
1
1
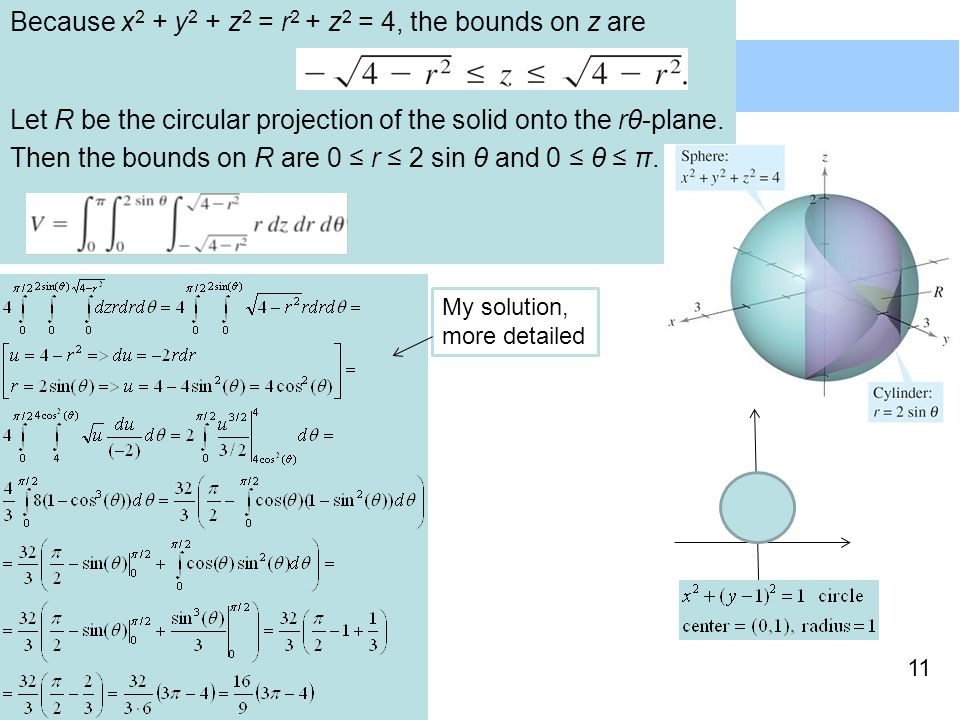
X 2 Y 2 Z 2 R 2 Cardays
Users Math Msu Edu

Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download
Solved 4 A Ex 6 4pts Evaluate The Integral 32 Y22 Ds Where S Is The Part Of The Plane 2 4 7 3 That Lies Inside The Cylinder 3 2 Course Hero
Sensors Free Full Text Experimental Research On Rapid Localization Of Acoustic Source In A Cylindrical Shell Structure Without Knowledge Of The Velocity Profile Html

3 Find The Volume Enclosed By The Following Two Parabolic Cylinders Y 2x X2 And Y2x2xand The Planes X Y Z Homeworklib

Amazon Com Welded Cylinder Crosstube 2 Bore X 24 Stroke Industrial Scientific




