六角形 五角形 の 内角 の 和
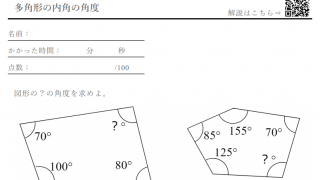
⑴ 六角形の内角の和は何度ですか。 ⑵ 正六角形の1つの内角(アの角度)は何度ですか。 ⑶ 三角形ABFは何という形の三角形ですか。 ⑷ イの角度は何度ですか。 ⑸ ウの角度は何度ですか。 ⑹ 直線BFと直線CEは何という関係にありますか。.
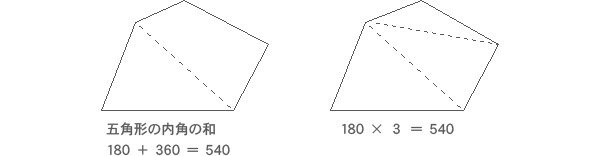
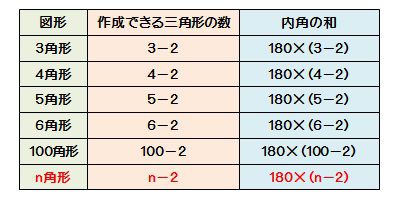
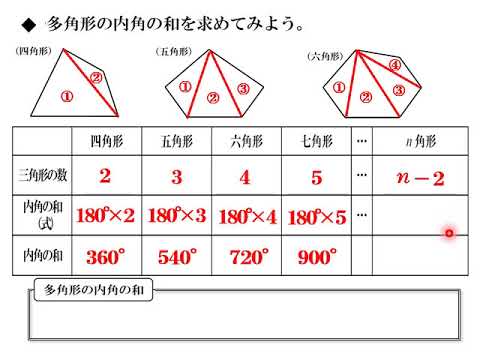
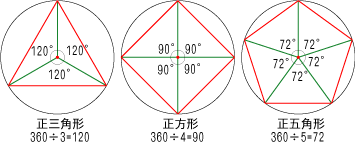
六角形 五角形 の 内角 の 和. 内角の和は,三角形3 つ分だから, 180ß*3=540ß 同様に,n角形の内角の和は, 180ß*(n2) となる。 多角形というときには,右の ようなへこんだ図形は考えな い。 チェック2 多角形の内角の和 教科書 16 多角形の内角と外角 P92~94・101~102. 多角形の内角の和 ここでは四角形以上の”多角形の内角の和”について考えてみましょう。 ではさっそく、 下に五角形と六角形の図があるので、それぞれの内角の和を考えてみましょう。 考え方は四角形の 算数では様々な公式を覚えます。 しかし. 2年 多角形の外角|数学イメージ動画集|大日本図書 五角形の外角を全部合わせると 360° です。 同様に,他の多角形でも外角の和は 360° になります。 このことから,多角形の外角の和はいつも 360° になるということがわかります。 実施時期 2年生2.
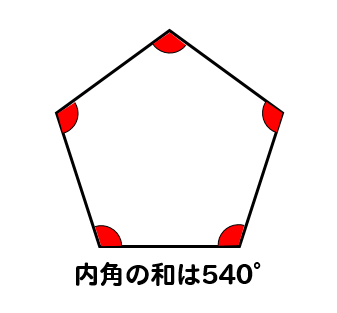
・5つの頂角を1つの三角形の内角に集める。 ・五角形の内角・外角を利用する。 ・その他 ・自分の解き方を説明している。 ・友だちの解き方を聞き,納得したり,新しい方法を考えている。 ・180度と答えた生徒が多い。. まずは、五角形の内角の和を考えましょう。 $$(五角形の内角の和)=180\times 3=540°$$ 次に、内角の和からすでに分かっている4つの角を引いていけば\(x\)の角度を求めることができます。 $$540()=86°$$. 星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して.
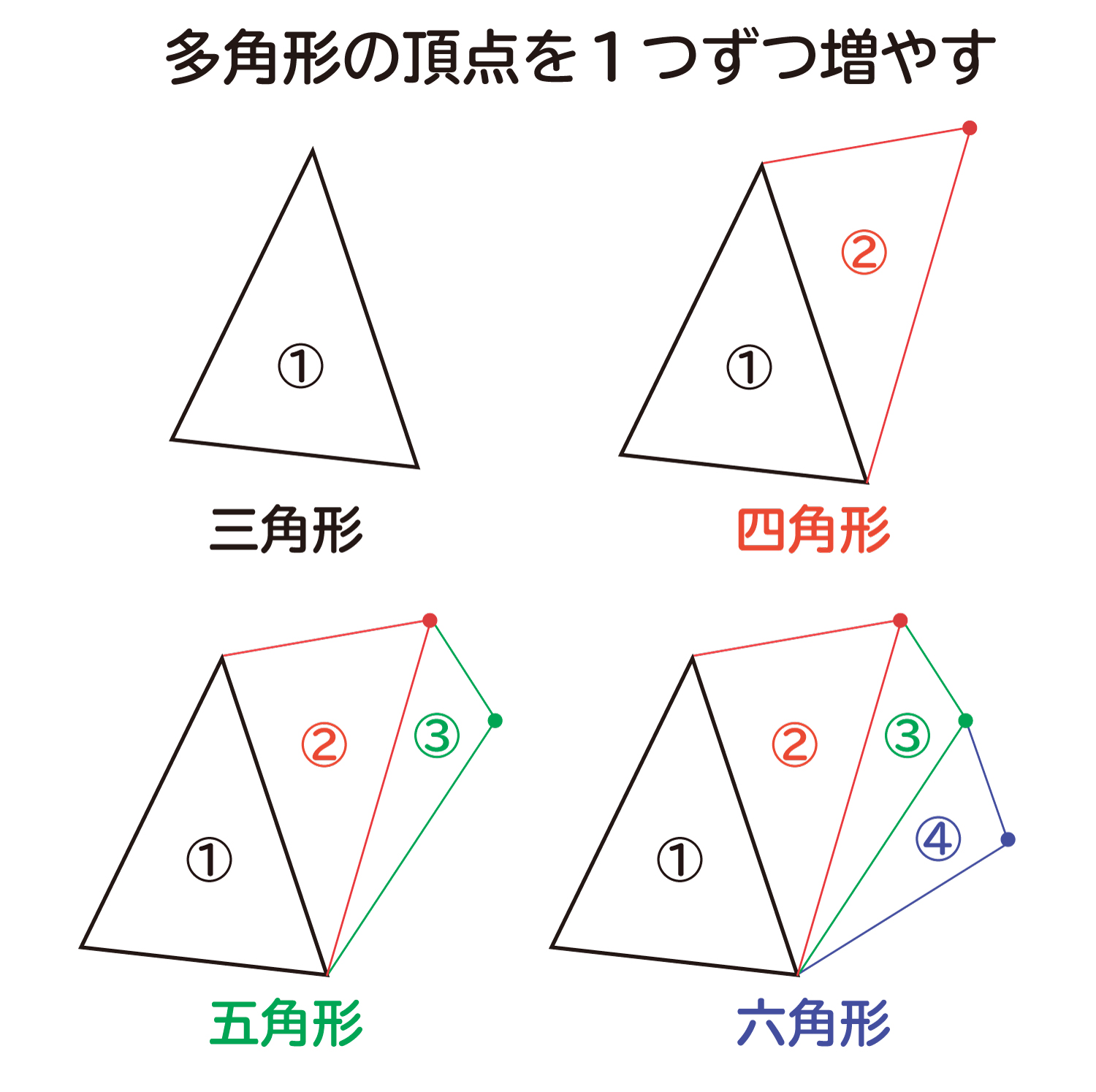
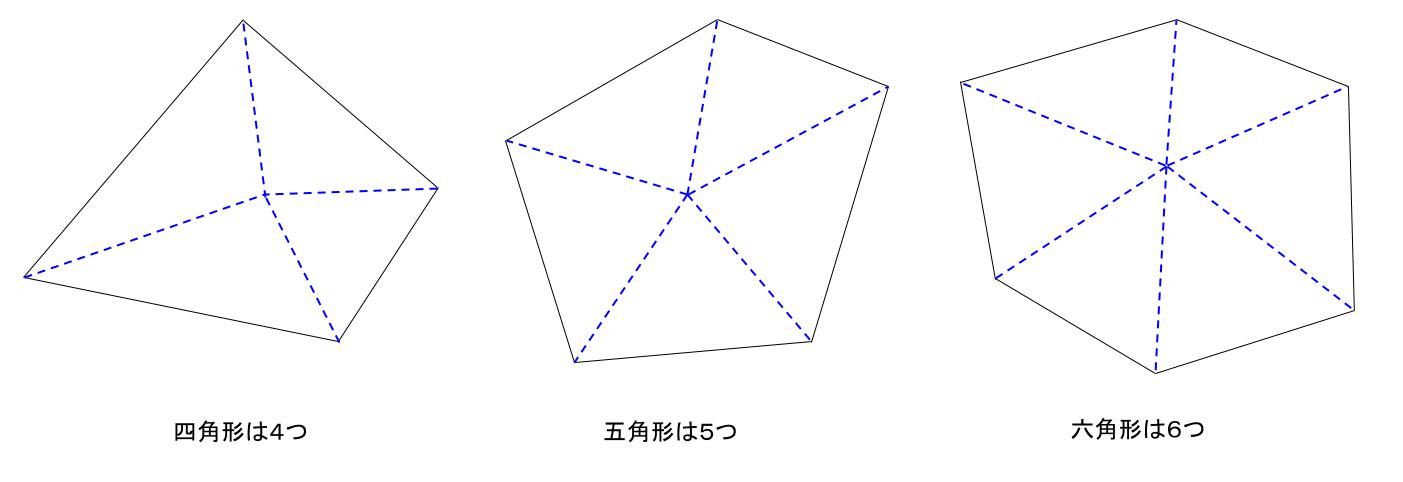
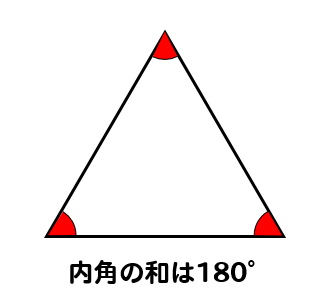
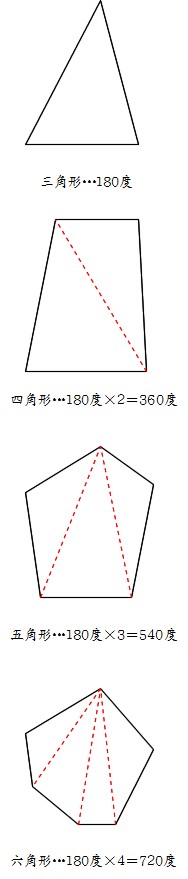
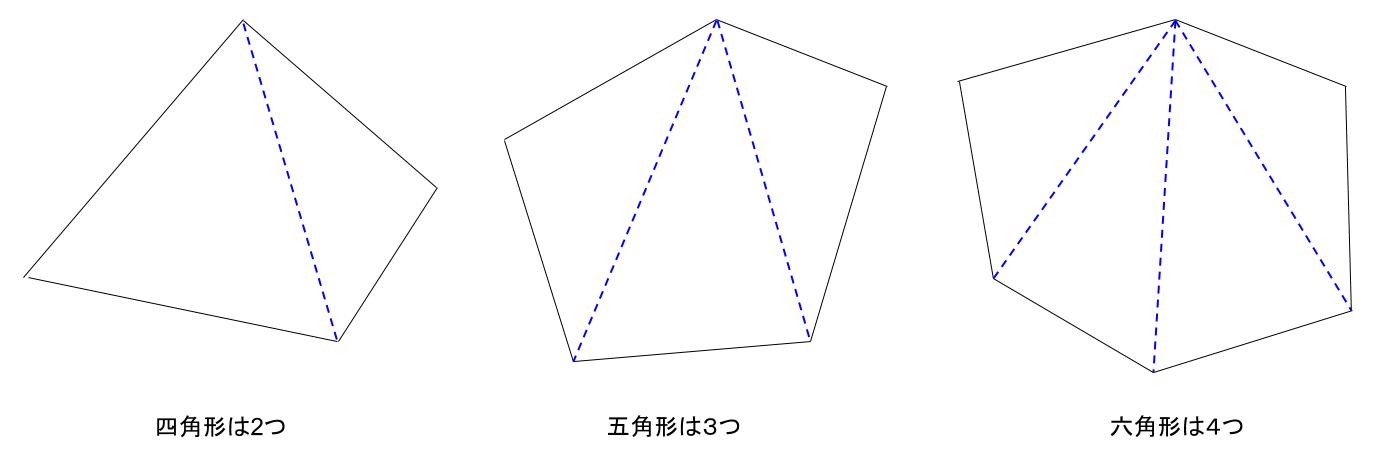
いろんな図形の内角の和 ⑴五角形は、三角形「3こ」に分けることができるので 180°×3こ=540° です ⑵六角形は。 三角形「4こ」に分けることができるので 180°×4こ=7° です このように、実際に図を書いて 三角形に分けていくことで求めることは. 内角 とは、多角形の隣り合った2辺がつくる角度のうち、多角形の内側の方の角度です。 下の図は、五角形の 内角 を表したものです。 5つの角に1つずつ 内角 があります。 内角 の和は、多角形の角の数をnとすると、 内角の和=180°×(n-2) で表され. 多角形の内角の和の公式と意味 多角形の基本の形は三角形です。 四角形は三角形が2つ 五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\).
頂点とする三角形の角の和から五角形の外角の 和を2つ分ひき,180°と求めることができる。 B ①では,図形の性質を利用することで星型五角形 の内角の和を演繹的に求める例をあげた。では, 結ぶ点の数を増やしたときに内角の和はどうな るだろうか. 五角形や六角形を対角線で三角形に分けて、三角形の内角の和が180°であることを基に、そのいくつ分かを考えさせる。 第3時の四角形の内角の和で、「努力を要する」状況(C)であった児童が「おおむね満足できる」状況(B)となるよう指導する。 また、本時において「十分満足できる」状況(A)になった児童がいれば記録に残す。 学び合い 5 自分の考えをグループで説明し合う。 6 全. ・ 「五角形」「六角形」「多角形」の・探究的な活動 ことを理解している。 4 定義を知る。 ・説明する活動 / ・ 五角形,六角形の内角の和を,三 8 角形に分割して調べ,多角形の内角 の和について表にまとめる。 ・ 多角形の内角の和のきまりを考え る。.
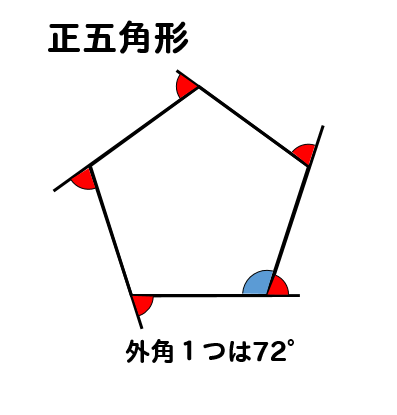
十五角形 (じゅうごかくけい、 pentadecagon )は、 多角形 の一つで、 15 本の 辺 と 頂点 を持つ 図形 である。 内角の 和 は2340°、 対角線 の本数は90本である。. 正五角形のそれぞれの内角 540度÷5=108度 正六角形の内角の和 180度×(6ー2)=7度 正六角形のそれぞれの内角 7度÷6=1度 正多角形の辺の数がたくさん増えても、この計算式で「内角の和」が分かります。 そして「内角の和」から、それぞれの「内角」も分かります。 算数のテストでも出るので覚えておきましょう! 正多角形の外角 スクラッチで正多角形. 多角形の内角の和と問題の求め方 十角形の内角の和を求めましょう。 辺の数が分かれば上記の公式を使って簡単に解ける問題です。 n=10なので 多角形の内角の和=180× n-2=180× 8=1440° 内角の和と三角形の関係は? 1分でわかる和の値、証明、外角との関係.
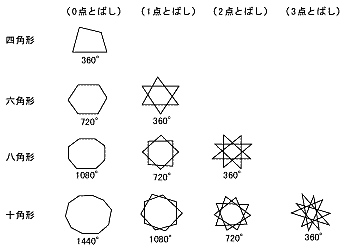
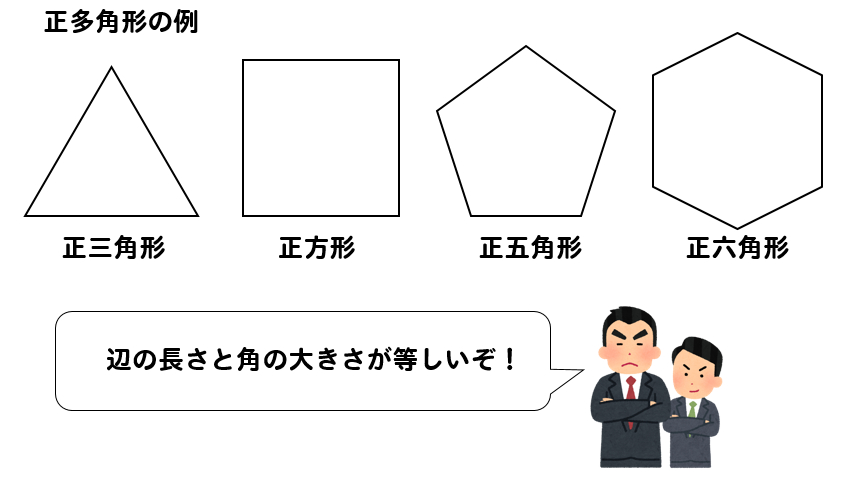
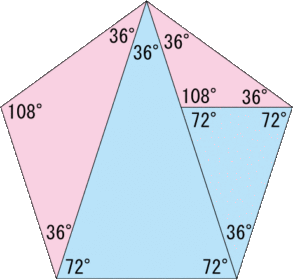
すべて 多角形を,正多角形といいます。 2 下の円を使って,正九角形をかきましょう。 ( 点) 3 下の図は正五角形です。 あからうの角度は何度ですか。 (30 点) あ い正五角形の性質 正三角形・正方形・正六角形に引き続き、正五角形編です。 相似 まずは角度に注目。 内角の和. 三角形・四角形の内角の和は小学校で習ったと思いますが、それぞれ180°、360°です。 さて、五角形、六角形など、角の数が増えていったら、内角の和はどうなるでしょうか? これを求めるために、三角形の内角が180°というすでに分かっていることを利用することで、わざわざ分度器などを用いなくても知ることが出来ますよ! 四角形を例に考えてみましょう。 四角形の内角の和が分からない人. 既習事項の確認をする。 「星形五角形の角の和」 している。(関心・意欲・態 星形六角形や七角形をノートに 書かせる。 課題を提示する。 ①n=6のとき、星形六角形の角を求 めよう。 ②n=7のとき、星形七角形の角を求 めよう。.
そんなこちらの事情はさておき、本題。 内角、外角 上の三角形で、赤色の角度を内角、青色の角度のように各辺の延長した線と隣の辺との角を外角といいます。 内角の和 三角形の内角の. 問題の印をつけた部分の和は三角形7つ分の内角の和-( の和+ の和) となり、180°×7-360°×2=540°となります。 内側に三角形タイプ 角の和 内側に三角形ができているタイプでは、補助線をひき、リボンの定理を使います。 例題4. 星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e).
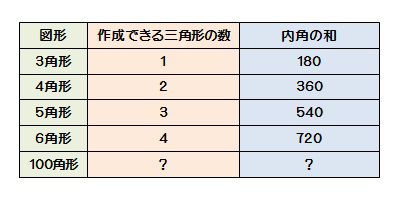
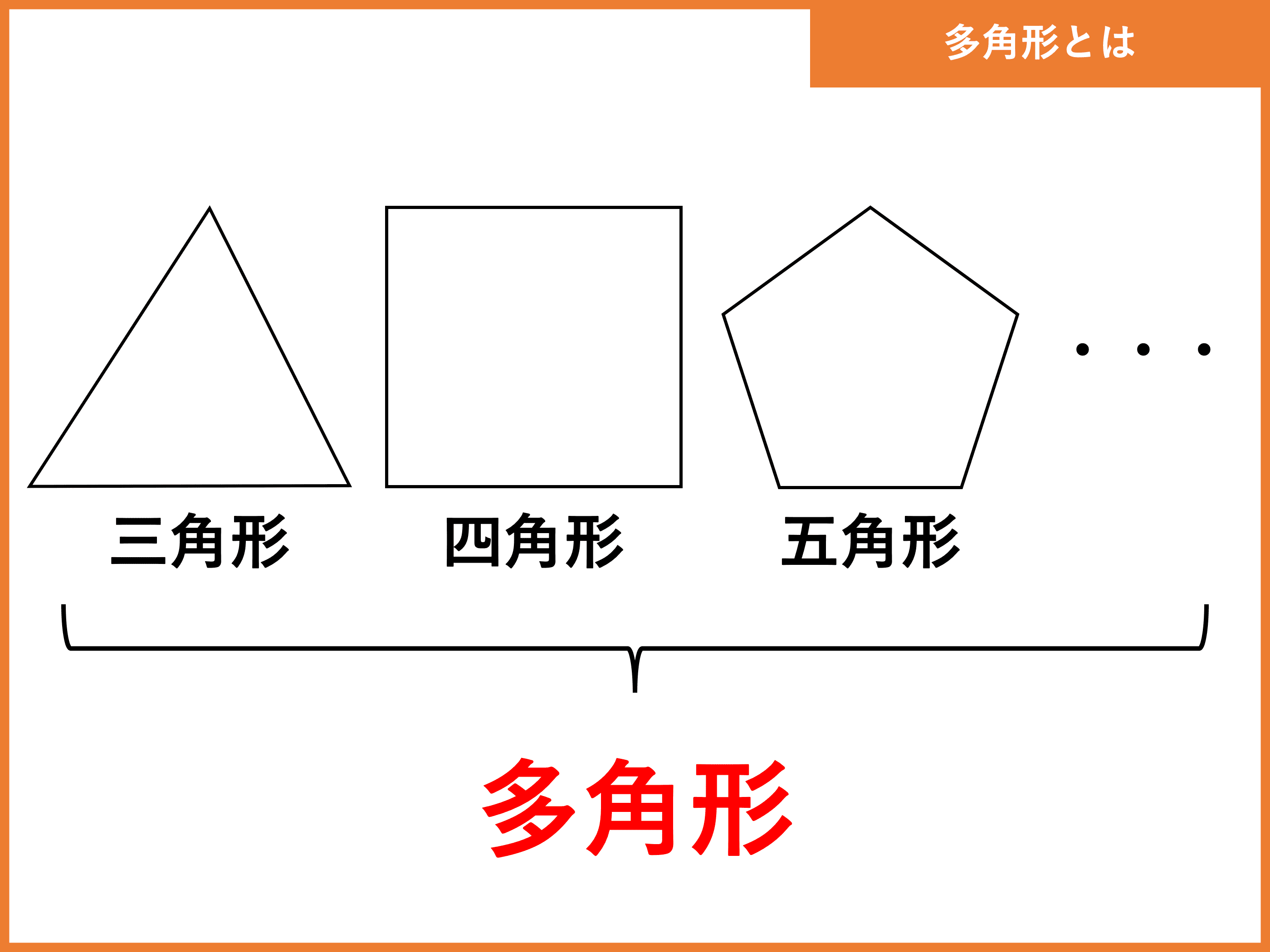
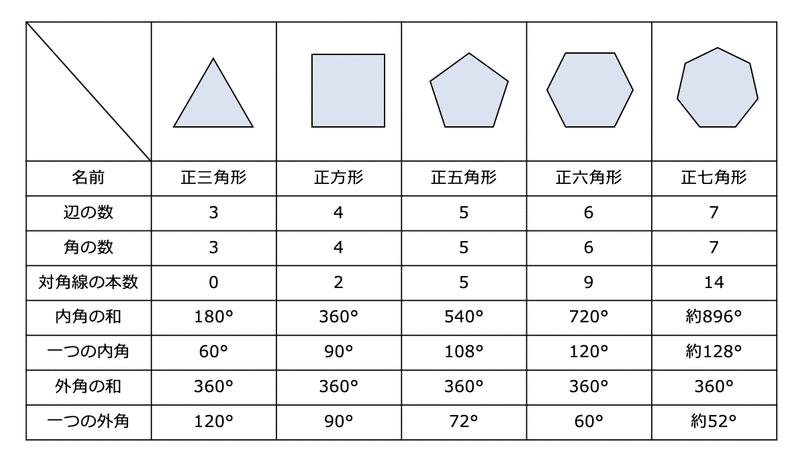
教え方3 三角形・四角形・五角形・六角形などのように 「直線で囲まれた形」を 多角形 (タカクケイ)といいます。 下の表は、多角形と内角の和の関係を表しています。 ①気がついたことを言わせましょう ②表のあいているところを計算で求めましょう. 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。 正多角形の内角 を知りたいときってあるよね?? 多角形の内角の和は公式つかえばドヤ顔できるけど、 せ、正多角形の内角はどうすれば・・・?. c22 正五角形の角が簡単に計算で求められたのがおもしろかったです。 c23 正三角形や正方形,正五角形ではみんな角が同じ大きさだとわかりました。 c24 五角形や六角形を分けて,角の和が計算で求められたのがよかった。.
つまり 角形の から2を引いて180°をかけたものが内角の和となります。 五角形: (52)×180=540° 六角形: (62)×180=7° それぞれ で割れば一角の角度が出ます。 540÷5=108° 7÷6=1° 10人 がナイス! しています. 課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を. 五角形の内角の和は「540°」 ってことさ! なんで内角の和が540°になの?? 公式をつかえば1秒ぐらいで計算できそうだけど、 そもそもなんで「540°」になってるんだろう?? チョー気になるよね笑 その理由は、 五角形の中に三角形が3つも潜んでいる.
よって、六角形も五角形のときと同様に考えると、内角の和は になります。 こうして考えていくと1つの規則性に気づきませんか? その規則性とは、 角形は個の三角形からできていて、内角の和はである ということです! 内角の和の公式はここから来ています。 したがって、もし公式を忘れても規則性さえ覚えていれば自分で公式を作ることもできます。 ここは公式だけでなく、ぜ. ① 三角形,四角形についての知識を五角形, 六角形にあてはめる。 ↓ 7 図・表・式・グラフに表現したり, よみとる ② 多角形の内角の和を求める方法をまとめ るために表に表す ↓ 2 帰納に推論する 5 一般化する ③ 多角形の内角の和を求める方法を導き出. つまり、五角形の場合は180°×3=540°となるので五角形の内角の和は540°、六角形の場合は180°×4=7°となるので六角形の内角の和は7°となります。 なんとなく規則性が見えてきましたね。 三角形の時は三角形が1個 四角形の時は三角形が2個.
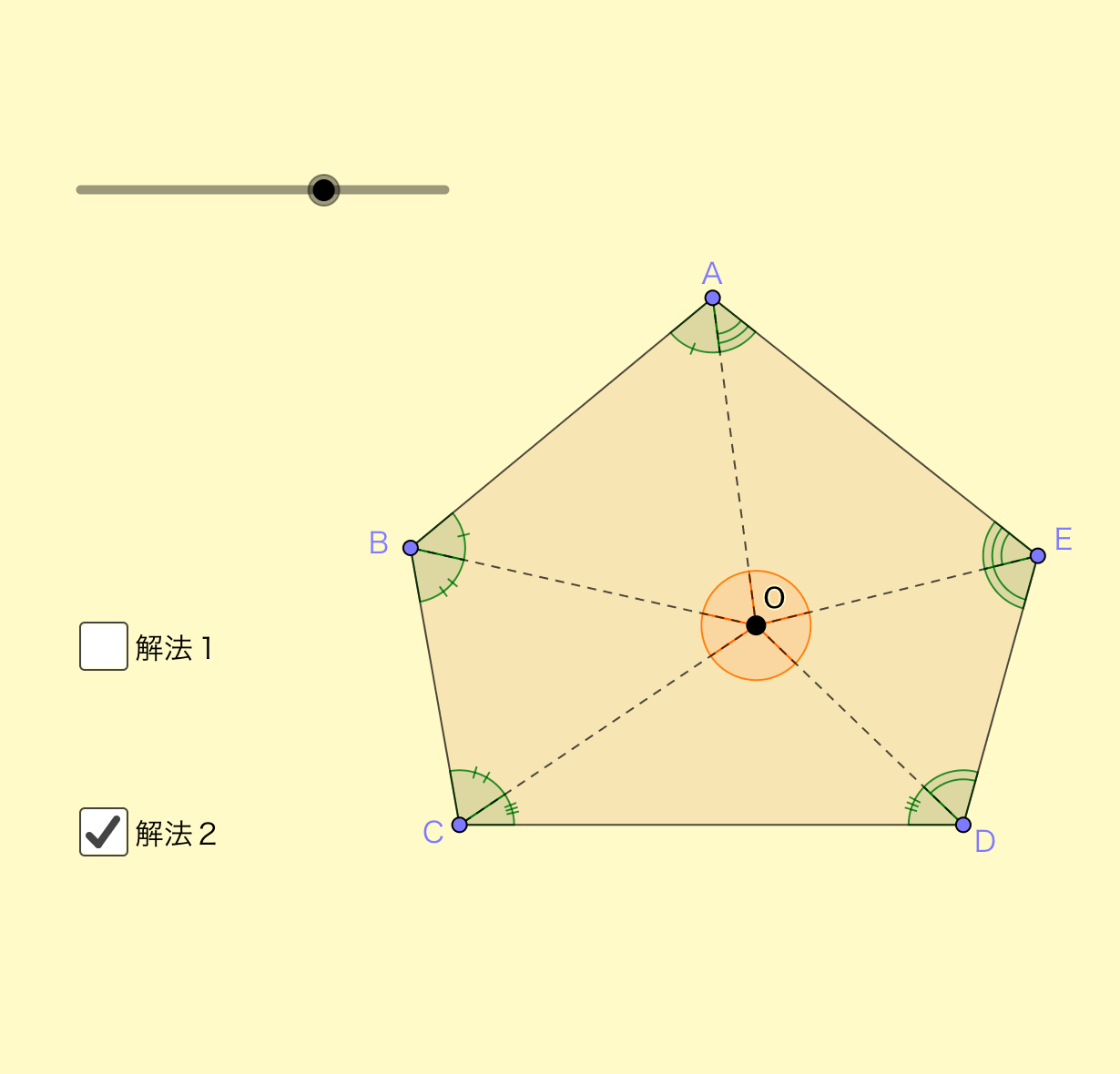
2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, 星形五角形を星形六角形,星形 形の内角の和から,五角形の外角の. 三角形の内角の和は 180°だから, b 2+c+d 2=180° ④ ③と④を加えると性質2 が得られる。 (2) n角形の場合 五角形の場合と同じように六角形の場合を調 べると,次の性質が成り立つ。 性質3六角形について, (5 つの内角の和) =(他の1 つの外周角)+360°.

多角形の内角の和 算数の公式覚えてますか

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
多角形の内角の和 算数の公式覚えてますか
六角形 五角形 の 内角 の 和 のギャラリー
正 角形 正多角形 を表にしてみる エクセル関数の使い方
中二 五角形の内角の和の求め方 をアップ 久保塾 今治市の学習塾
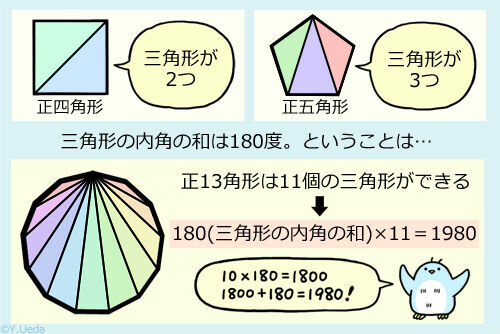
これで脳の記憶機能が復活 正13角形の内角の和を求めるクイズ 16年8月8日 ウーマンエキサイト 2 3
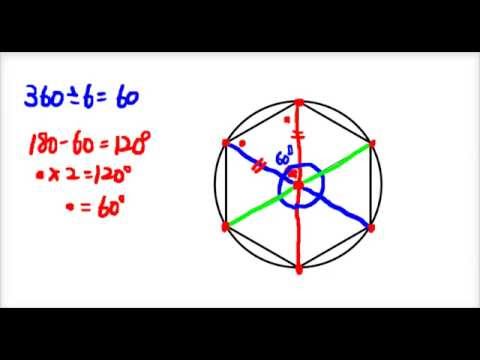
簡単にわかる 正六角形のかきかた ふるやまんの算数塾 Youtube
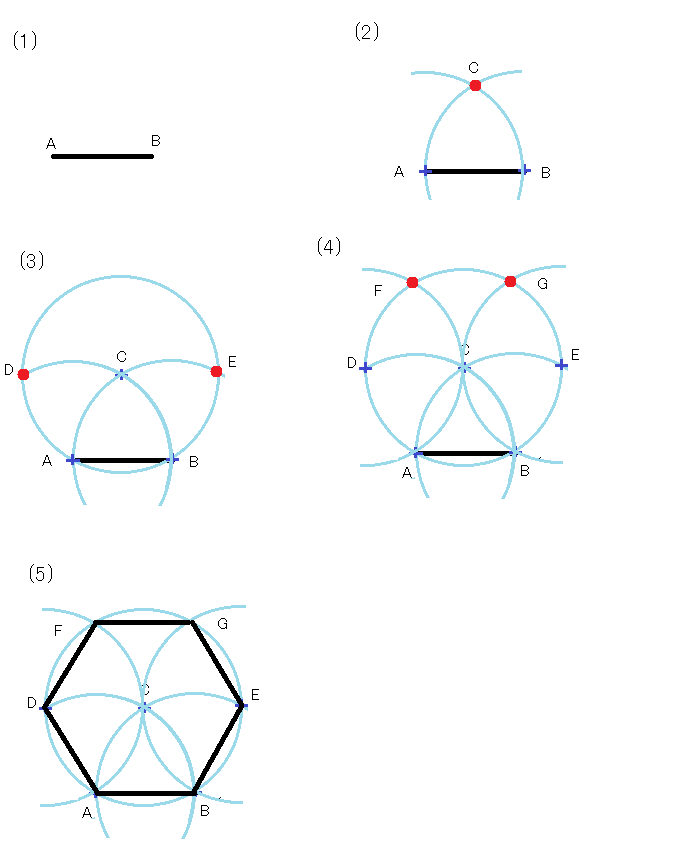
コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

多角形の内角の和 外角の和の公式 数学fun
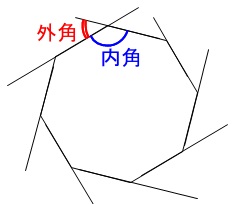
多角形の内角の和の公式と外角の和を利用した角度の求め方

多角形の内角の和 は何度なのか を説明します おかわりドリル

多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

重なった正六角形と正五角形の角度 奈良学園登美ヶ丘中学 09年 早稲田中学 10年 算数解法の極意
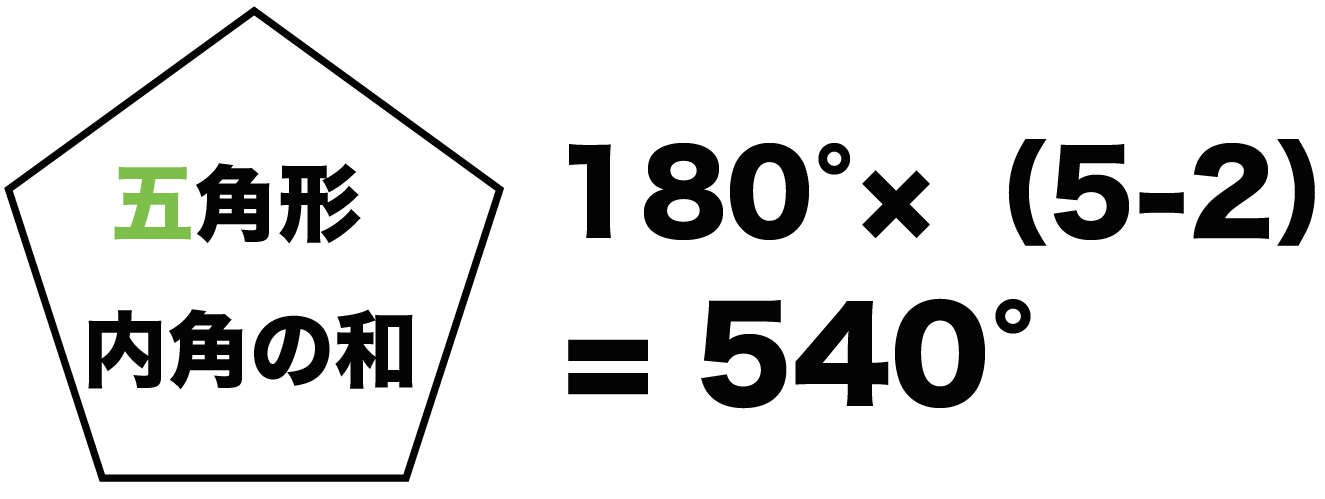
中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
図の5の問題について 六角形の内角の和は180 6 Yahoo 知恵袋

小学5年生 正多角形 算数 Active Learning 学院
3

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
正多角形の描き方
サッカーボールの型紙 エクセルvbaで正六角形を作図しますpart 2 日だまりのエクセルと蝉しぐれ

内角の和 180 N 2 外角の和 360 教遊者

多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
正6角形の内角 外角
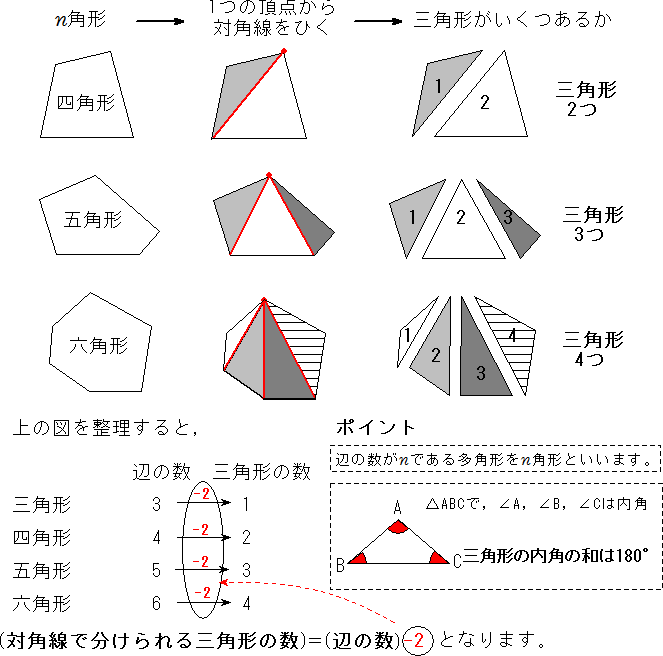
三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト
正多角形の1つの内角 外角を求める方法を問題解説 数スタ

正六角形の書き方と展開図の書き方 コンパス 定規 分度器 手紙 書類の情報ならtap Biz

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
1

ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス
課題学習の指導 数学

多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
1
なぜ n角形の内角の和は 180 n 2 なのか を説明します おかわりドリル
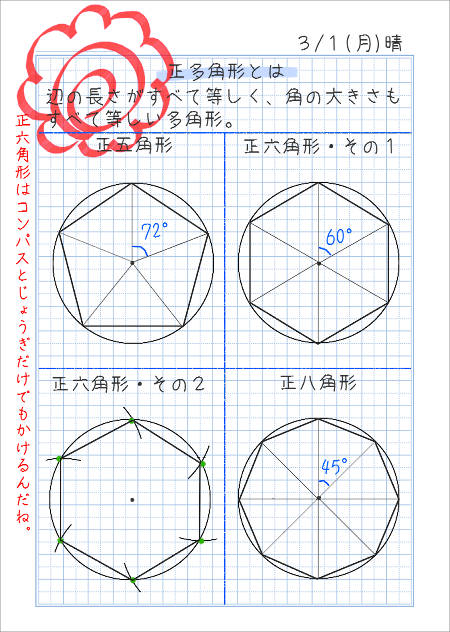
いろいろな正多角形をかいてみよう 家庭学習レシピ

中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
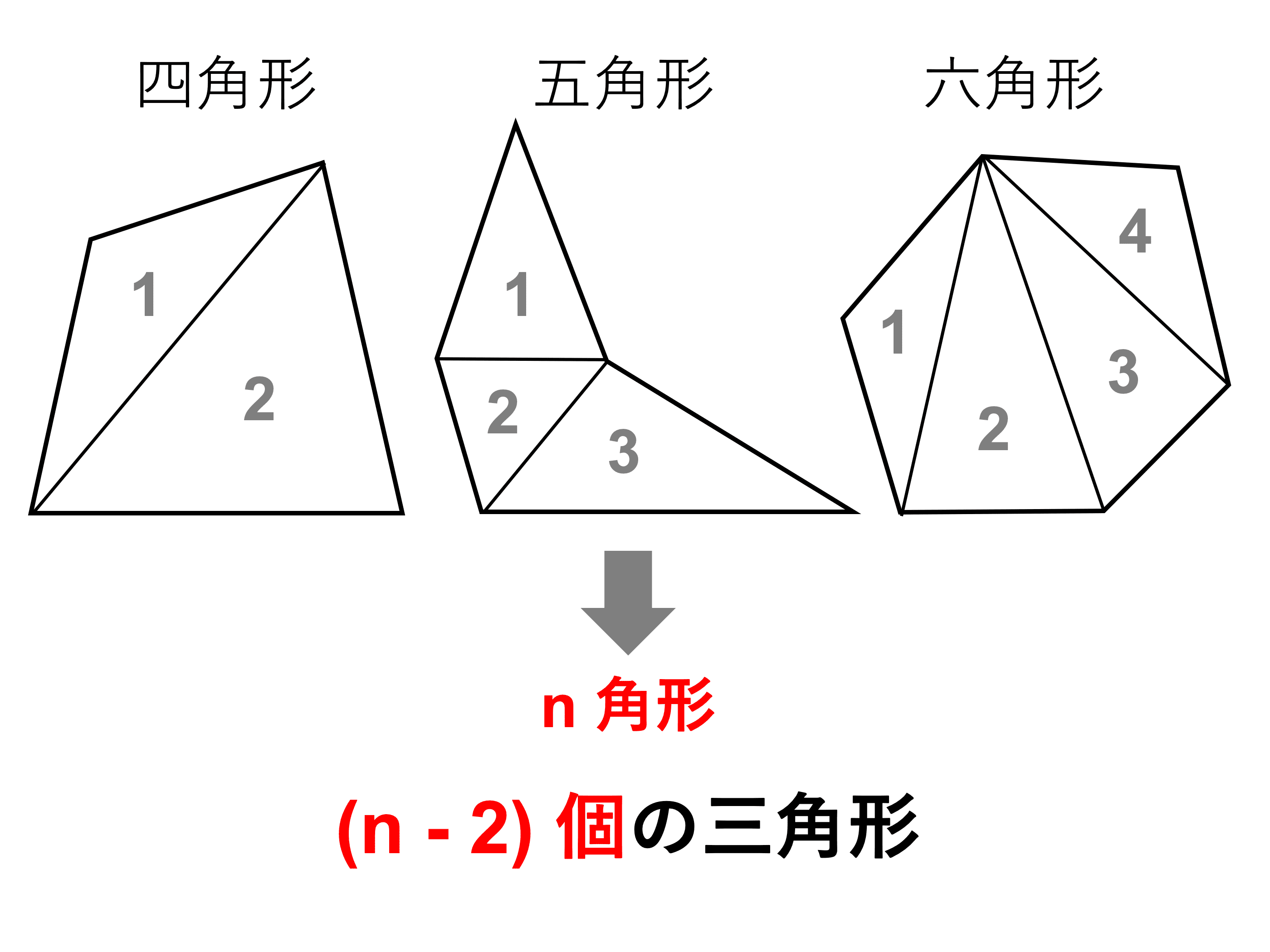
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典

中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
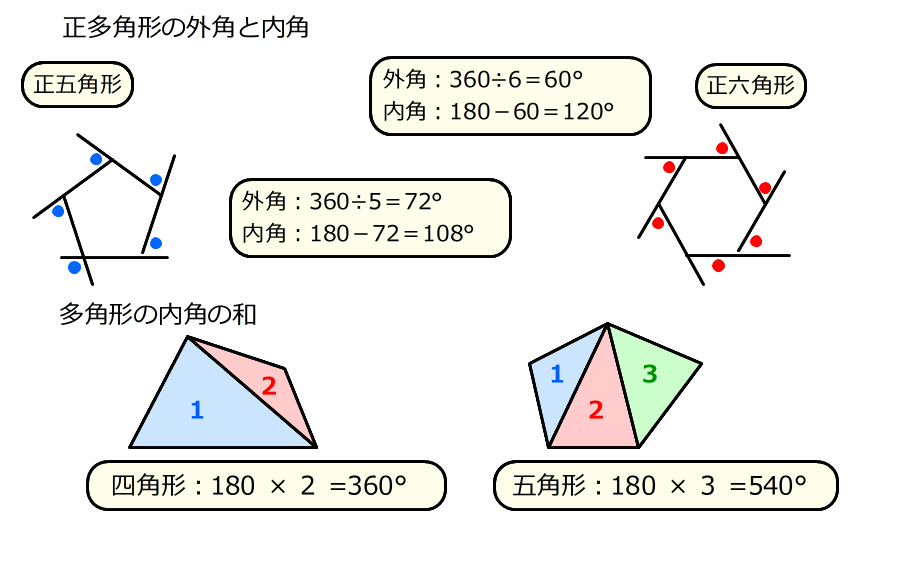
南山中学女子部過去問題演習

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
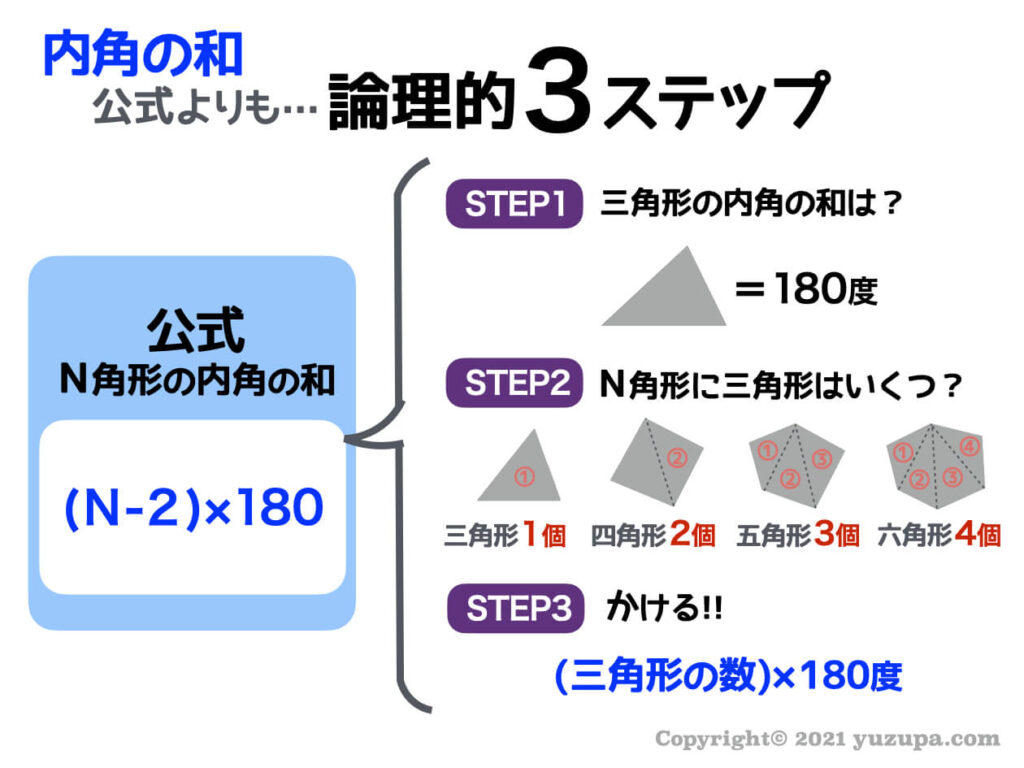
中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋

多角形の内角の和 外角の和の公式 数学fun

多角形の内角の和 外角の和の公式 数学fun
正六角形の描き方を教えて下さい 書きたい正6角形の1辺の長さ Yahoo 知恵袋
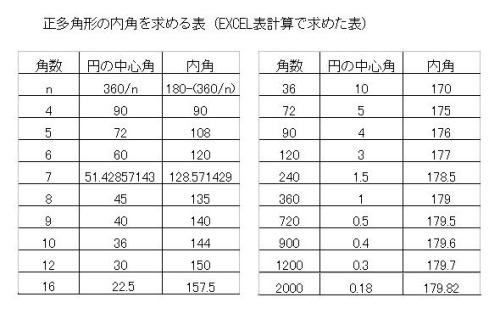
正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ
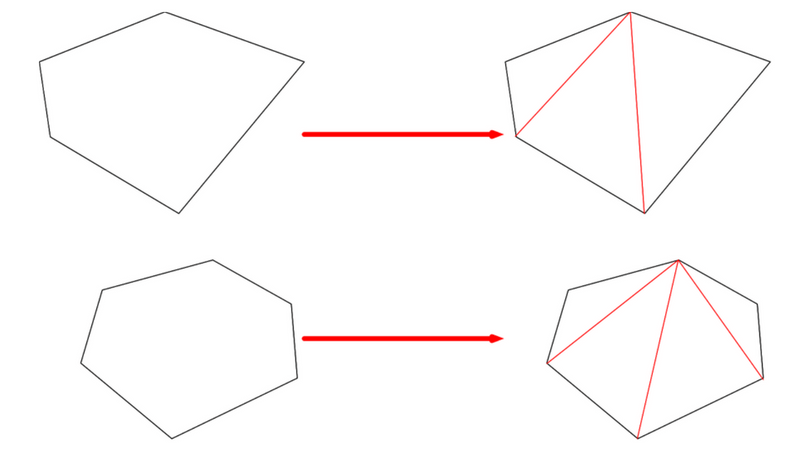
三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局

星形n角形の角度の和と多角形の内角の和の似ているところ 前のページの表をみると 両者とも 180度の倍数になっています 正六角形の内角は 右のように 三角形が4つありますので 180 4 なので 720度ということがわかります
中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su

南山中学女子部過去問題演習
正多角形の1つの内角 外角を求める方法を問題解説 数スタ

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版

多角形の内角の和 は何度なのか を説明します おかわりドリル

中2数学 複雑な多角形 角の和 応用問題

正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より
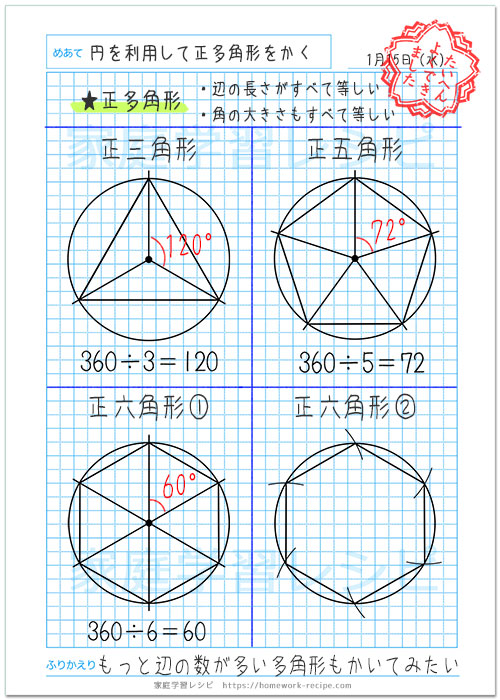
円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
正多角形の1つの内角 外角を求める方法を問題解説 数スタ
5年算数 多角形の内角の和 教え方
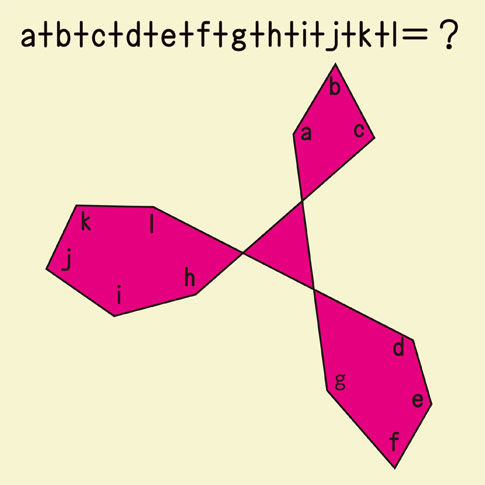
12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday

多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ

内角の和 180 N 2 外角の和 360 教遊者
Math 多角形の内角の和 働きアリ
正多角形の1つの内角 外角を求める方法を問題解説 数スタ

基本のpolygons 多角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強

多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
数学得意な方お願いします 正五角形の1つの内角は何度になりますか その角度を求 Yahoo 知恵袋

小5 算数 小5 33 五角形 六角形 多角形 Youtube

3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
多角形の内角の和 算数の公式覚えてますか

数学 中2 51 多角形の内角と外角の和 基本編 Youtube

内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典

多角形の内角の和の公式と外角の和を利用した角度の求め方
サッカーボールの型紙 エクセルでひと手間かけて正六角形を作図します 日だまりのエクセルと蝉しぐれ
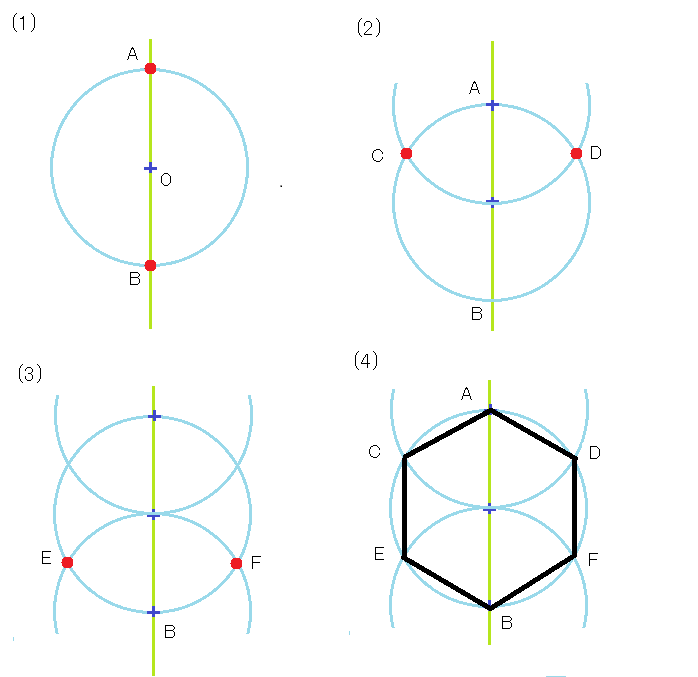
コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫
コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫

上6 角形五角形角度 シモネタ

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
1
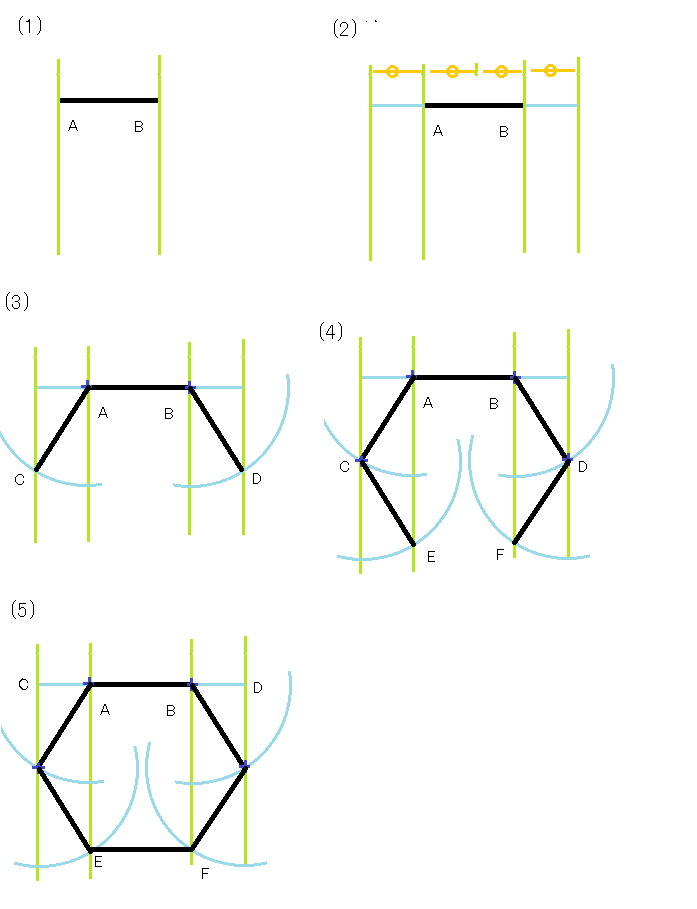
中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
動画 多角形の内角の和 Youtube

正六角形のかき方 小学校算数 コンパスと定規だけでかく方法 Youtube

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

課題学習の指導 数学
正多角形の作図 5年生 算数の広場

3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく

定規とコンパスで書く五角形と六角形の書き方 Ibispaint
多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
図形 正五角形の分解 父ちゃんが教えたるっ
実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note
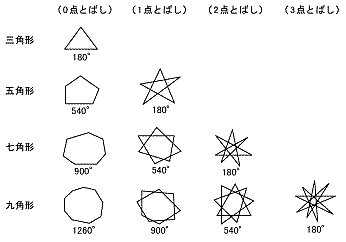
課題学習の指導 数学

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

多角形の内角の和 算数の公式覚えてますか
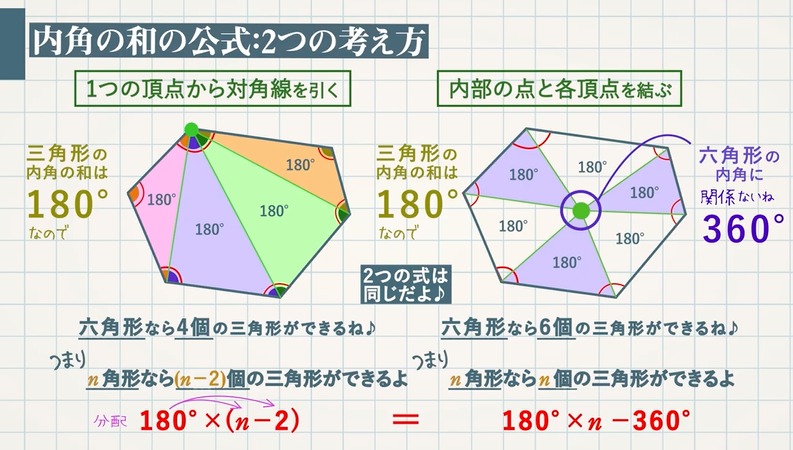
内角の和 180 N 2 外角の和 360 教遊者

正五角形のかき方 小学生の自主学習 分度器 コンパス 定規を使う方法 Youtube
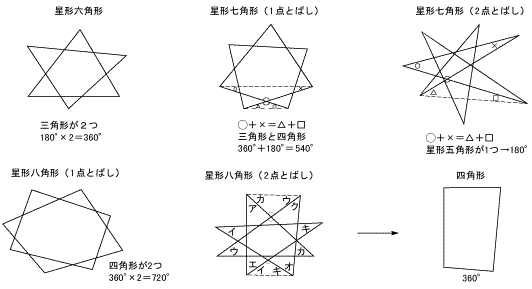
課題学習の指導 数学

正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information
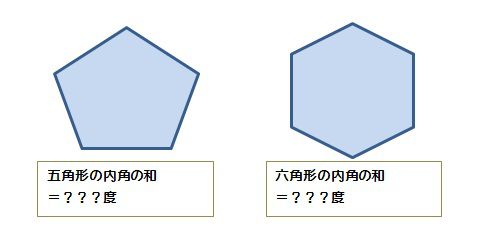
多角形の内角の和 算数の公式覚えてますか

十五角形 Wikipedia

小5算 多角形と円4 連問2 正5角形の書き方 正6角形を作図する方法 Youtube




