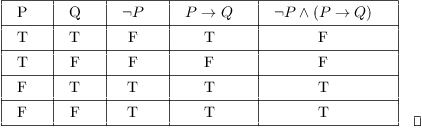
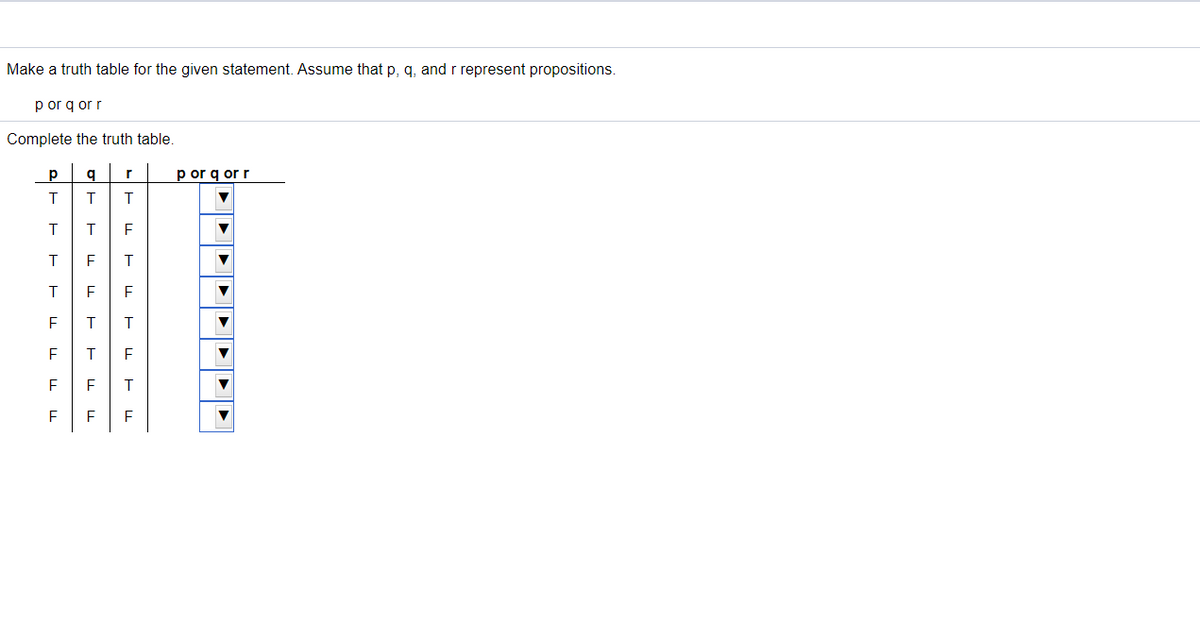
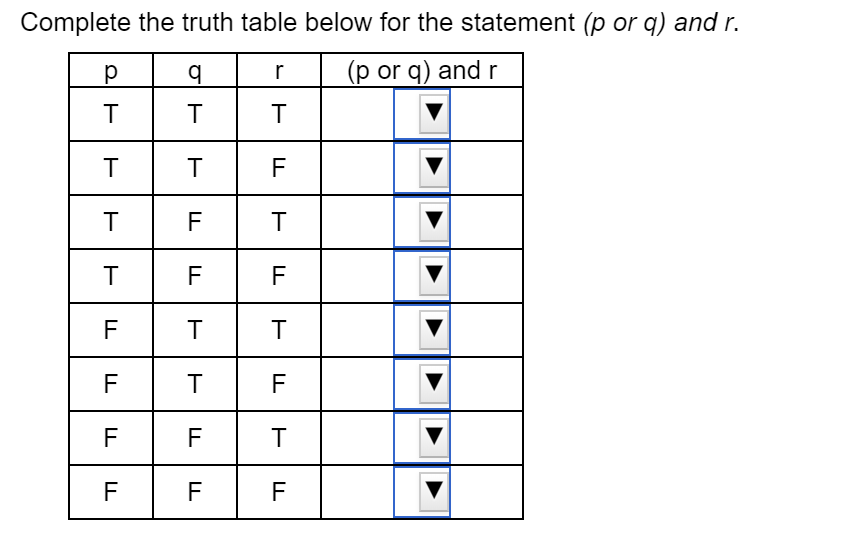
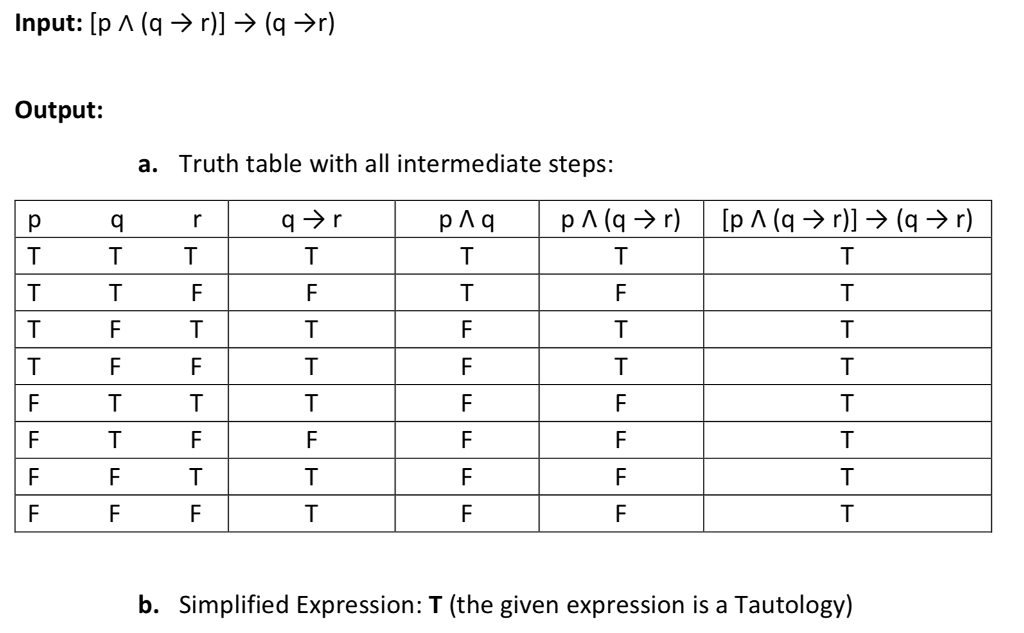
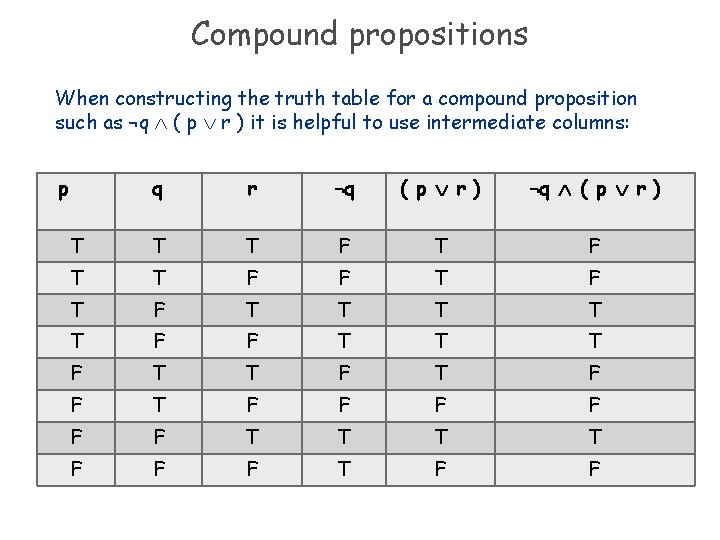
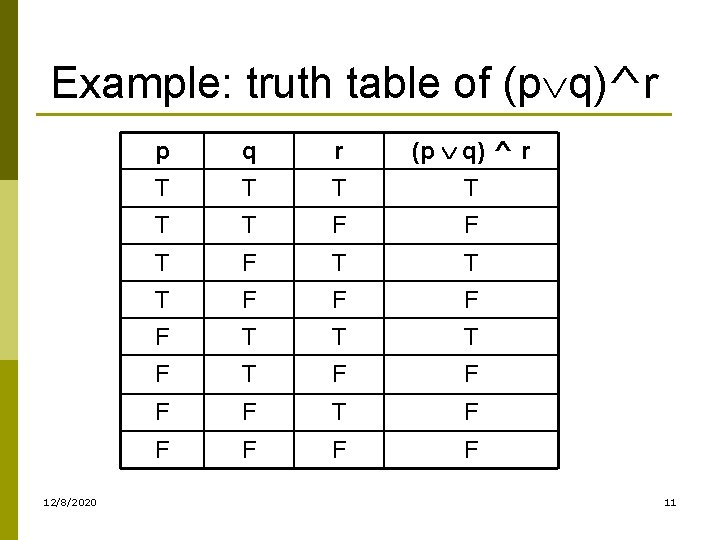
Pqrpqr Truth Table
' 05Œ09, N Van Cleave 2 Testing Validity with Truth Tables 1 Break the argument down into component statements, assigning each a letter 2 Rewrite the premises and conclusion symbolically 3.

Pqrpqr truth table. De Morgan’s Laws • ¬ (p ∧ q) ≡ ¬ p ∨ ¬ q • ¬ (p ∨ q) ≡ ¬ p ∧ ¬ q !. Tautology, Contradiction, Contingency, Valid, Invalid, Falsifiable, Unfalsifiable, Satisfiable, Unsatisfiable with their definition, truth table and examples are. Originally Answered Explain, without using a truth table, why (p ∨¬q) ∧ (q ∨¬r) ∧ (r ∨¬p) is true when p, q, and r have the same truth value and it is false otherwise ?.
With Truth Table p q ((p → q) ∧ p) → q T T T F F T F F Are the squirrels hiding?. Prove without using truth table that $(p↔q)∧(q↔r)∧(r↔p) ≡ (p→q)∧(q→r)∧(r→p)$ I tried to prove this by rewriting the first part using $∧$, $∨$ and the fact that $(p↔q)≡(p→q)∧(q→p)$ to conclude. You can do that and help support Ms Hearn Mat.
(b) Assuming p has truth value T, q has truth value F, and r has truth value F, use the tree to find the truth value of the statement form 41) (a) Draw a tree for the statement ~(p ∧ q) ∨ (~p ∧ r) (b) Assuming p has truth value T, q has truth value T, and r has truth value F, use the tree to find the truth value of the statement form. This is just the truth table for \(P \imp Q\text{,}\) but what matters here is that all the lines in the deduction rule have their own column in the truth table Remember that an argument is valid provided the conclusion must be true given that the premises are true The premises in this case are \(P \imp Q\) and \(P\text{}\). Each of them can be verified using the truth table method Law of Detachment p→ q p ∴ q Law of Contraposition p→ q ∼ q ∴∼ p Law of Syllogism p→ q q→ r ∴ p→ r Disjunctive Syllogism p∨q ∼ p ∴ q Simplification p∧q ∴ p Addition p ∴ p∨q Logical Fallacies • It is vital to realize that not every argument is valid.
If p and q are propositions, then the implication “If p then q “ denoted by p→q , called the conditional statement of p and q , is defined by following truth table p q p→ T T T T F F F T T F F T NOTE p→q is false when p is true and q is false O. This truthtable calculator for classical logic shows, well, truthtables for propositions of classical logic Featuring a purple munster and a duck, and optionally showing intermediate results, it is one of the better instances of its kind Use the buttons below (or your keyboard) to enter a proposition, then gently touch the duck to have it. If p then q truth table have false values, then it is a contradiction However, an Online Two’s Complement Calculator allows you to calculate 2’s complement of the given decimal, binary or hexadecimal number Contingency A Contingency is an equation, which has both some false and some true values for every value of its propositional variables.
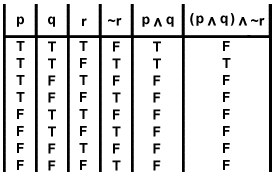
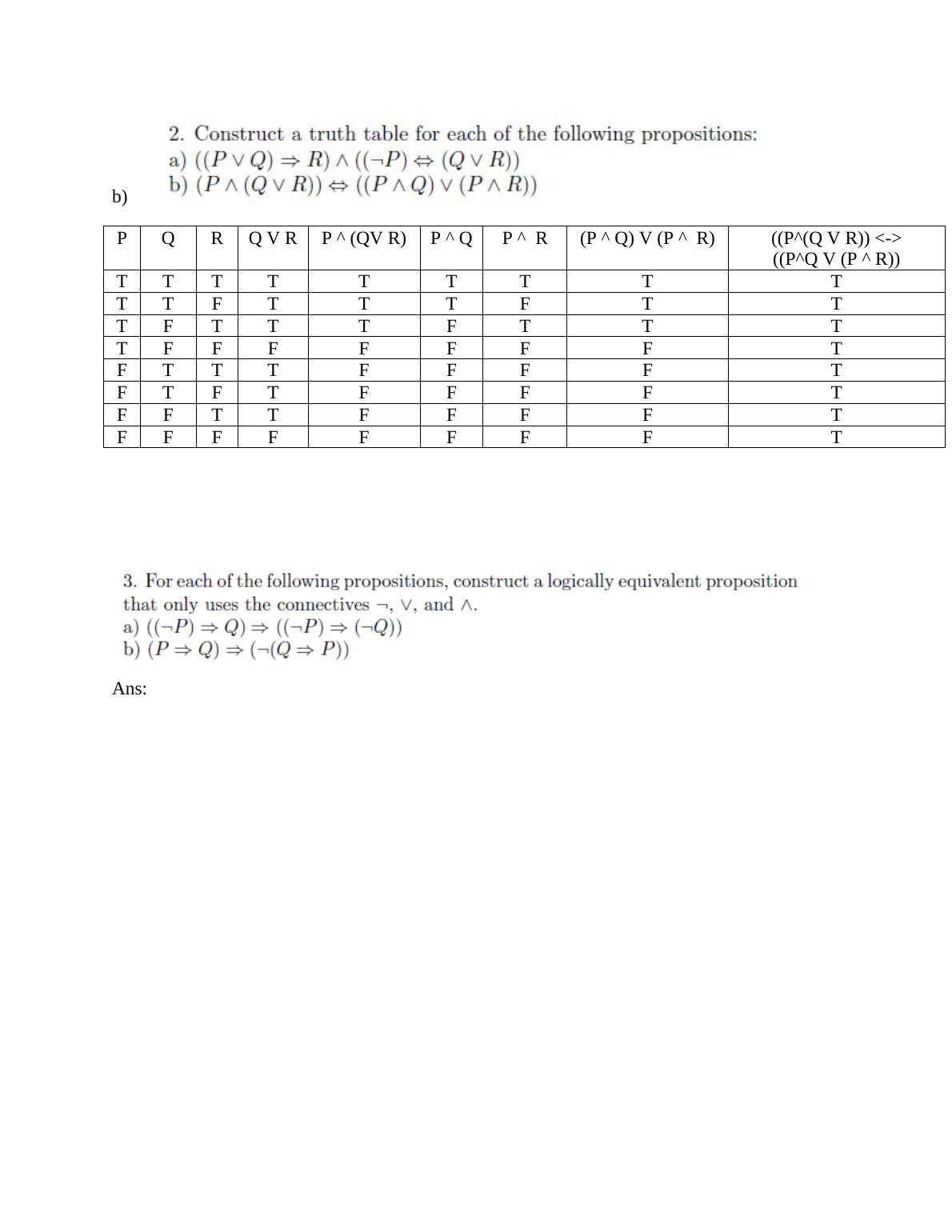
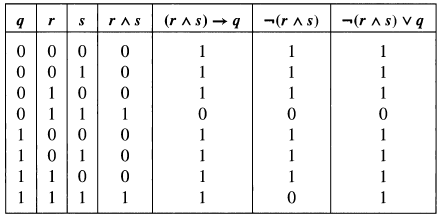
Truth table for conjunction p q p ^ q T T T T F F F T F F F F c Xin He (University at Buffalo) CSE 191 Discrete Structures 11 / 37 Disjunction Another binary operator isdisjunction _ , which corresponds toor, (but is slightly different from common use) p _ q is trueif and only if p or q (or both of them) are true Example Alice is smart OR honest. So the formula is in fact equivalent to ( Q ↔ P) ∧ ( R ↔ Q) ∧ ( P ↔ R) In other words, it says that Q and P must have the same truth value, and that this also holds for R and Q, and for P and R This is the same as saying that all of P, Q and R must have the same truth value 9. Construct the truth table for the statements (pVq) V (~p^q) → q p q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18 (15 points) Write each of the following three statements in the symbolic form and determine which pairs.
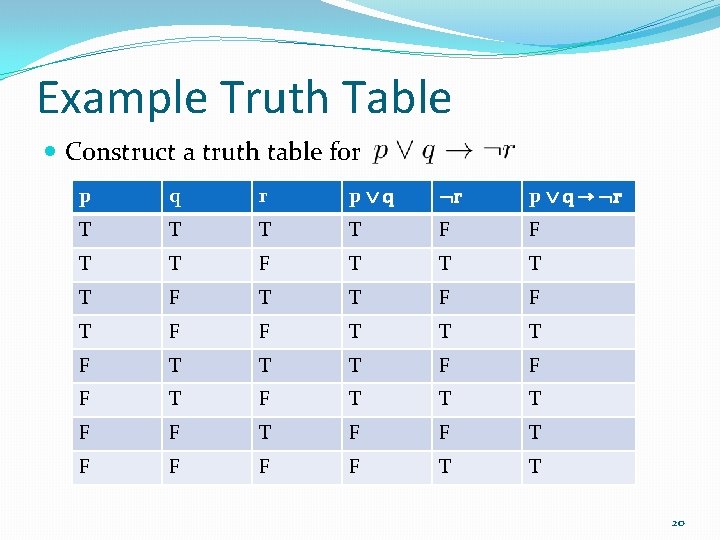
≡¬q∨(p∨r) by commutative and associative laws ≡q→ (p∨r) by implication law 7 (0 points), page 35, problem 30 Show that (p∨q)∧(¬p∨r) → (q∨r) is a tautology sol (p∨q)∧(¬p∨r) → (q∨r) ≡¬(p∨q)∧(¬p∨r)∨(q∨r) by implication law ≡¬(p∨q)∨¬(¬p∨r)∨(q∨r) by de Morgan’s law. 2 Given p I studied for this exam, q I got a good grade on this exam, r I understand truth tables, and s I am not good at doing proofs, translate the following statements into words 3 p ↔ (∼ s∨ ∼ r) I studied for this exam if and only if I am good at doing proofs or I do not understand truth tables 4 (p → (r ∧(∼ s)) → q. Construct a truth table for ()p∧q →r p Q r (p∧q) (p∧q)→r T T T T T T T F T F T F T F T T F F F T F T T F T F T F F T F F T F T F F F F T Equivalent Statements Equivalent Statements will have the same result in the last column of their truth tables Example 12 Compare the truth tables for )~ (p∨q and ~ p∧~ q Truth table for ~ (p∨q).
Truth Table Generator This tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats For example, the propositional formula p ∧ q → ¬r could be written as p /\ q > ~r, as p and q => not r, or as p && q > !r. Construct a truth table for the formula First, I list all the alternatives for P and Q Next, in the third column, I list the values of based on the values of P I use the truth table for negation When P is true is false, and when P is false, is true In the fourth column, I list the values for Check for yourself that it is only false ("F") if P is true ("T") and Q is false ("F"). The very short answer is that a disjunction is true, except when both sides are false and a.
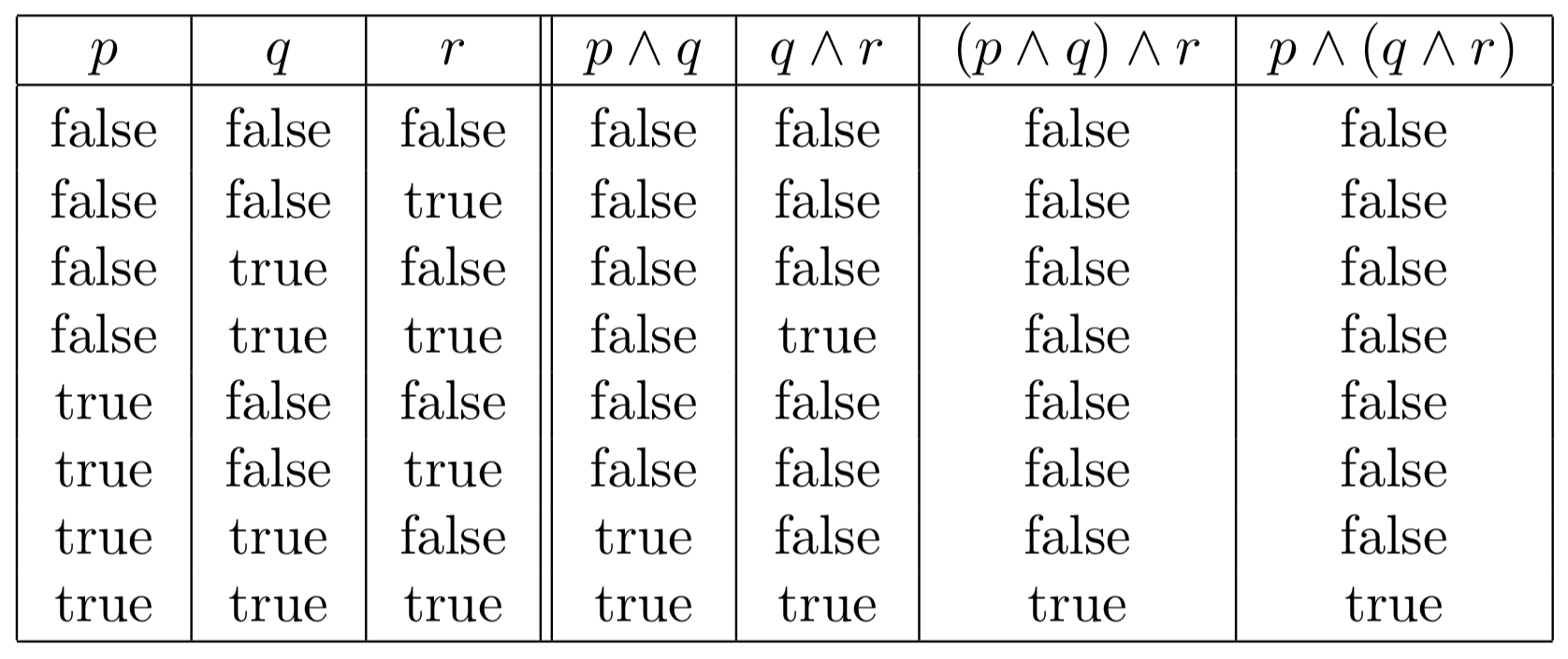
(iii) Truth table for (p → q) ↔ (¬ p → q) In the above truth table the entries in the last column are a combination of’ T ‘ and ‘ F ‘ So the given statement is neither propositions is neither tautology nor a contradiction It is a contingency (iv) Truth table for ((p → q) ∧ (q → r)) → (p → r) The last column entires. P q r q p r ∴ q aka Disjunction Elimination Corresponding Tautology ((p q) ∧ (r q) ∧ (p r )) q Example Let p be “I will study discrete math” Let q be “I will study Computer Science” Let r be “I will study databases” “If I will study discrete math, then I will study Computer Science”. 32 Truth Tables A truth table lists all possible combinations of truth values In a twovalued logic system, a single statement p has two possible truth values truth (T) and falsehood (F)Given two statements p and q, there are four possible truth value combinations, that is, TT, TF, FT, FFAs a result, there are four rows in the truth table.
Chemistry Examples Popular Problems Chemistry Balance construct a truth table for (pvq)→r construct a truth table for (pvq) → r ( p v q) → r The chemical equation cannot. In this case, the truth values for (~r∧(p→~q))→p and r∨p are exactly the same, so we can conclude that the two statements are equivalent (~ r ∧( p→~q ))→ p ≡r ∨ p So, if we ever encounter(~ r ∧( p→~q ))→ p , we can replace it with r ∨ p without changing the logical meaning of the statement !. Here's how you can use this tool Follow me Import your text or your logical operator by clicking the Import box.
Definition 212 An expression involving logical variables that is false for all values is called a contradiction 🔗 Statements that are not tautologies or contradictions are called contingencies 🔗 Definition 213 We say two propositions p p and q q are logically equivalent if p ↔ q p ↔ q is a tautology We denote this by p ≡. So P and Q and R has the same Does not have interest table up Oh, I accidentally wrote, True for all of them when I meant fault because Q and R are all falls here So no, we can see that P and Q and R have the same truth table for all possible combinations of P Q and are therefore they are logically equivalent. Truth Table for p ^ (q ^ r)If you enjoyed this video please consider liking, sharing, and subscribingUdemy Courses Via My Website https//mathsorcerercom.
The truth table is p q r p → q p∨ r r → T T T T T T → T T F T T F T F T F T T T F F F T F → F T T T T T F T F T F F → F F T T T T F F F T F F This is clearly not a valid argument as stated above, if the victim had money in their pockets, and the motivation of the crime was robbery. Truth values are the same for all possible combinations of truth values of P, Q In that case we write, S ≡ T Looking at the truth table below we see that according to this definition, P ⇔ Q ≡ (P ⇒ Q) ∧ (Q ⇒ P) P Q P ⇒ Q Q ⇒ P P ⇔ Q (P ⇒ Q) ∧ (Q ⇒ P) T. 111 Connectives, Truth Tables Connectives are used for making compound propositions The main ones are the following (p and q represent given propositions) Name Represented Meaning Negation ¬p “not p” Conjunction p∧q “p and q” Disjunction p∨q “p or q (or both)” Exclusive Or p⊕q “either p or q, but not both.
Example 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalent. Example truth table construct a truth table for p q r This preview shows page 28 40 out of 42 pages Truth Tables of Compound Propositions Construct the truth table of the compound proposition (p ∨ ¬ q) → (p ∧ q) The Truth Table for the compound proposition (p ∨ ¬ q) → (p ∧ q) p q ¬ q (p ∨ ¬ q) (p ∧ q) (p ∨ ¬ q. As an introduction, we will make truth tables for these two statements 1 p ∧ q 2 p ∨ q Solution to EXAMPLE 217 #1 p q p∧q T T T T F F F T F F F F Note that in this truth table there is only one row in which the statement p ∧ q is true This the row where p is true and q is true This conforms to our earlier observation that.
Notation p ≡ q !. Read “p if and only if q” Here's its truth table T F F T p q p ↔ q F F T T F F T T One interpretation of ↔ is to think of it as equality the two propositions must have equal truth values One interpretation of ↔ is to think of it as equality the two propositions must have equal truth values. I want to determine the truth value of (P → Q) → ¬R Since I was given specific truth values for P, Q, and R, I set up a truth table with a single row using the given values for P, Q, and R P Q R P → Q ¬R (P → Q) → ¬R T F T F F T Therefore, the statement is true Example Determine the truth value of the statement.
Proving $(p\leftrightarrow q)\land(q\leftrightarrow r)\to(p\leftrightarrow r)$ is a tautology without a truth table 0 Proving existence of a. Two propositions p and q are called logically equivalent if and only if vp = vq holds for all valuations v on Prop In other words, two propositions p and q are logically equivalent if and only if p 㲗 q is a tautology We write p ≡ q if and only if p and q. Two compound propositions, p and q, are logically equivalent if p ↔ q is a tautology !.
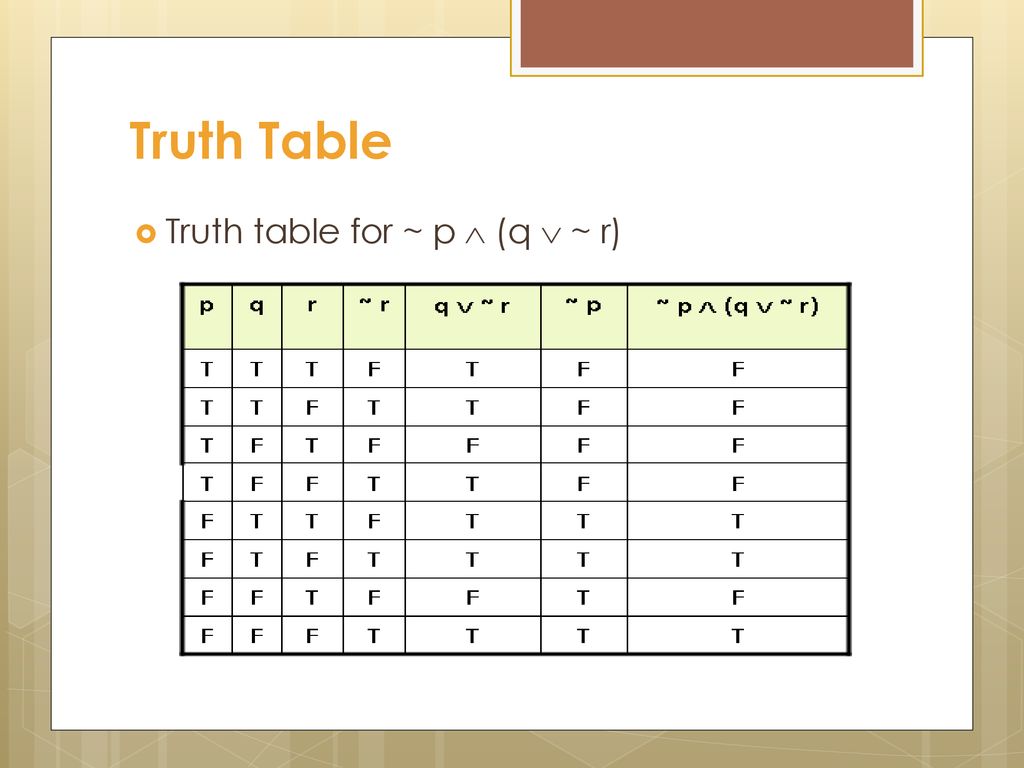
Show that each conditional statement is a tautology without using truth tables b p !(p_q) p !(p_q) p_(p_q) Law of Implication (p_p)_q Associative Law T_q Negation Law T Domination law 2 ICS 141 Discrete Mathematics I (Fall 14) d (p^q) !(p !q) (p^q) !(p !q) (p^q)_(p !q) Law of Implication (p^q)_(p_q) Law of Implication. 106 ~(~r) → (p ∧ q) ↔(~p) ∨ r, negation 107 a) The conjunction and disjunction have the same dominance b) Answers will vary 107 c) If we evaluate the truth table for p ∨ q ∧ r using the order (p ∨ q) ∧ r we get a different solution than if we used the order p. This problem has been solved!.
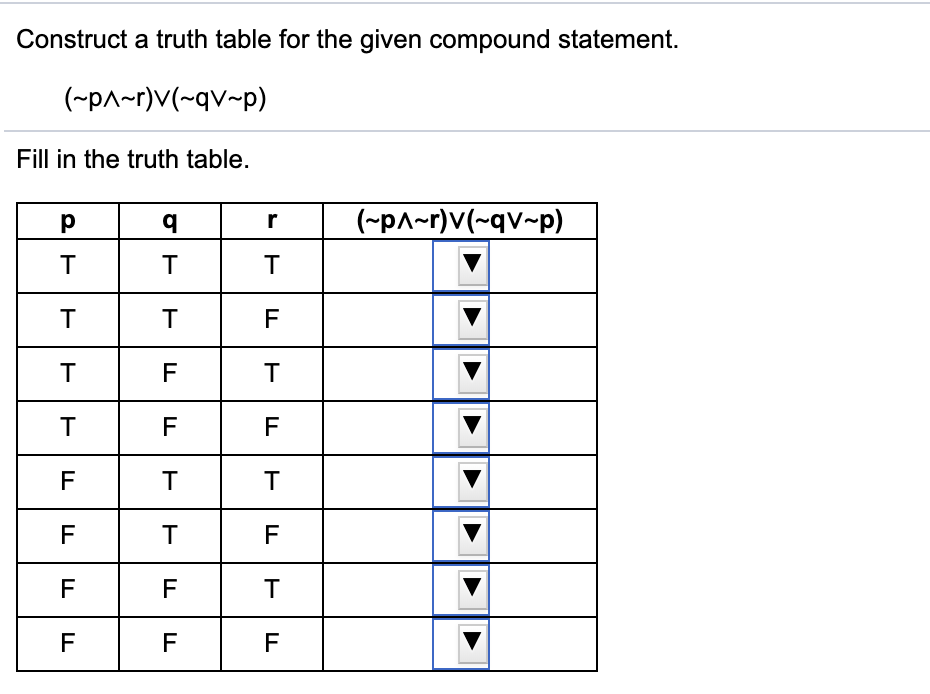
Construct the truth table of the following statement pattern p → (q → r) ↔ (p ∧ q) → r Mathematics and Statistics Determine whether the following statement pattern is a tautology, contradiction or contingency. Now, our final goal is to be able to fill in truth tables with more compound statements which have more than just one logical connective in them Statements like q→~s or (r∧~p)→r or (q&rarr~p)∧(p↔r) have multiple logical connectives, so we will need to do them one step at a time using the order of operations we defined at the beginning of this lecture. For example, the proposed formula could write p ∧ q → ¬r, not p / \ q > ~ r, p, and q => r, or p && q >!.
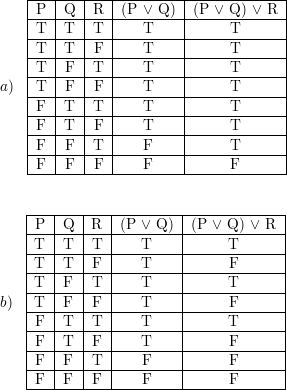
Using the Truth Table Verify that P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R) Maharashtra State Board HSC Commerce 12th Board Exam Question Papers 195 Textbook Solutions MCQ Online Tests 99 Important Solutions 2470 Question Bank Solutions Concept Notes &. See the answer See the answer See the answer done loading Construct truth table for each of the following compound statements (a) (p ∨ q) ∧ ¬ (p ∨ q) (b) (p ∨ q) → (¬p ∧ q) (c) (¬p ∧ q) → (¬q ∨ p) (d) p → (¬q ∨ r). P Q R (P ∨ Q) ∨ R → Use DeMorgan's laws or a truth table to determine whether the two statements are equivalent 31) ~(~p → q), p ∨ ~q P Q ~ (~P.
Click SHOW MORE to view the description of this Ms Hearn Mathematics video Need to sell back your textbooks?. R Connectors ⊤ and ⊥ can be entered as T and F How to use Truth Table Generator Calculator?.
Truth Tables Tautologies And Logical Equivalences

The Truth Table Represents Statements P Q And R Which Row Represent When P Q V P R Brainly Com
Library Abes Ac In
Pqrpqr Truth Table のギャラリー

Logical Equivalences
Prove That P Q R P Q R Using Truth Table Sarthaks Econnect Largest Online Education Community
What Is The Truth Table For P Q Q R P R Quora
Faculty Gordonstate Edu

Module Code Ma1032n Logic Lecture For Week Autumn Ppt Download
Answered Make A Truth Table For The Given Bartleby
Solved Consider The Following Pair Of Statements In Which P Chegg Com

What Is The Truth Table For This Logic Statement Stack Overflow
Eng Usf Edu

Truth Table Widget

Solved Use Properties Of Logic Not A Truth Table To Prove That P Q R P Q R
Solved Discrete Math And Computer Science Given A Chegg Com
Geometry Logic Statements Problems 4 Sparknotes
Proving Neg R To P Lor Neg Q To Neg P Land R To Q To Neg P Lor Q Is A Tautology Without A Truth Table Mathematics Stack Exchange

Solved Construct The Truth Table Of P Q V Q R R P Chegg Com
Answer In Discrete Mathematics For Javairia 1236
Www3 Cs Stonybrook Edu
Answer In Discrete Mathematics For Rjbuela

Quick Help Please The Truth Table Represents Statements P Q And R Which Statements Are True For Brainly Com
Truth Tables Tautologies And Logical Equivalences

Solved Construct A Truth Table For Each Of These Compound Propositions I P Q R S Ii P Q P Q Sikademy

Formal Logic The Propositional Calculus Britannica

Prepare The Truth Table For The Following Statement Pattern P Q R P

Truth Table Generator Free Online Logic Calculator Formula

Using Truth Table Prove The Following Logical Equivalence P Q Rarr R P Rarr Q Rarr R Youtube
Construct A Truth Table For Each Of These Compound Propositi Quizlet
Answer In Discrete Mathematics For Muhammad Abdullah 1713
Cs 2 Discrete Structures And Their Applications Propositional

The Truth Table Represents Statements P Q And R Which Statement Is True For Rows A C And E O Brainly Com

Short Truth Table Method Determine The Validity Using The Short Truth Table Method P Q R S Q S Pvr Homeworklib
Truth Table Interpretation Physics Forums
1 1 Propositional Logic Engineering Libretexts

Proof And Problem Solving Truth Table Example 02 Youtube

See Solution Construct A Truth Table For Each Of The Following Compound Statements Where P Q R Denote Primitiv 4092

Show That Each Conditional Statement Is A Tautology Without Using Truth Tables A Neg Pwedge Pv Q To Q B P To Q Wedge Qto R To Pto R C Pwedge Pto Q To Q D

Prove That P Oplus Q Oplus R Is Logically Equivalent To P Oplus Q Oplus R Mathematics Stack Exchange

Construct The Truth Table For The Followings Statements A P Q To P B P Q To Pvvq C P Q To R D P R To Qvvr

Formal Logic The Propositional Calculus Britannica
What Is The Truth Table Of P Qv R Quora
Solved Construct A Truth Table For The Given Compound Chegg Com
Answer In Discrete Mathematics For Angelica Aguilar

Prove The Following Is A Tautology Without Using A Truth Table P Q Q R Homeworklib
Discrete Mathematics Lecture Ppt Download

Create A Truth Table For This Statement P Q R Choose The Answer That Matches Correct Final Homeworklib
Solved Calculate By Hand The Appropriate Truth Table To Prove Or Disprove The Following Pq R Pr Qr If It Is Invalid Give A Counterexamp Course Hero
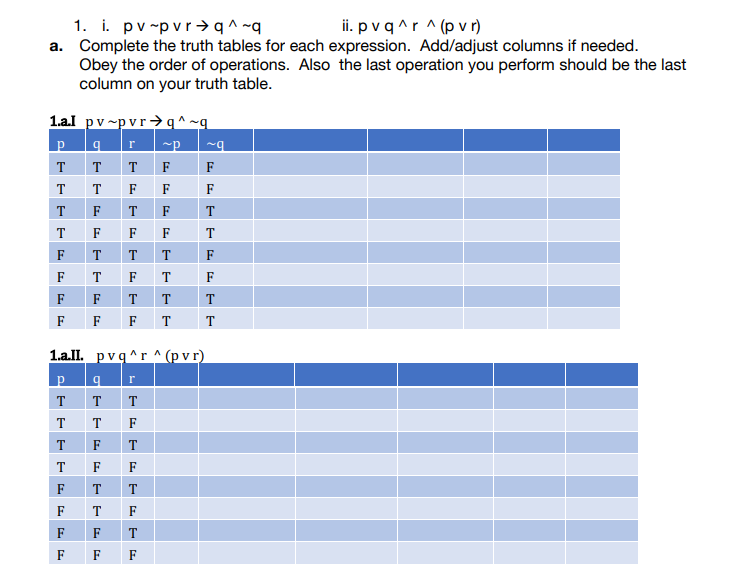
Question 1 I Pv Pvr Q Q I I Pv Q R P Vr A Complete The Truth Tables For Each Expression Add Adjus Answer Streak
1
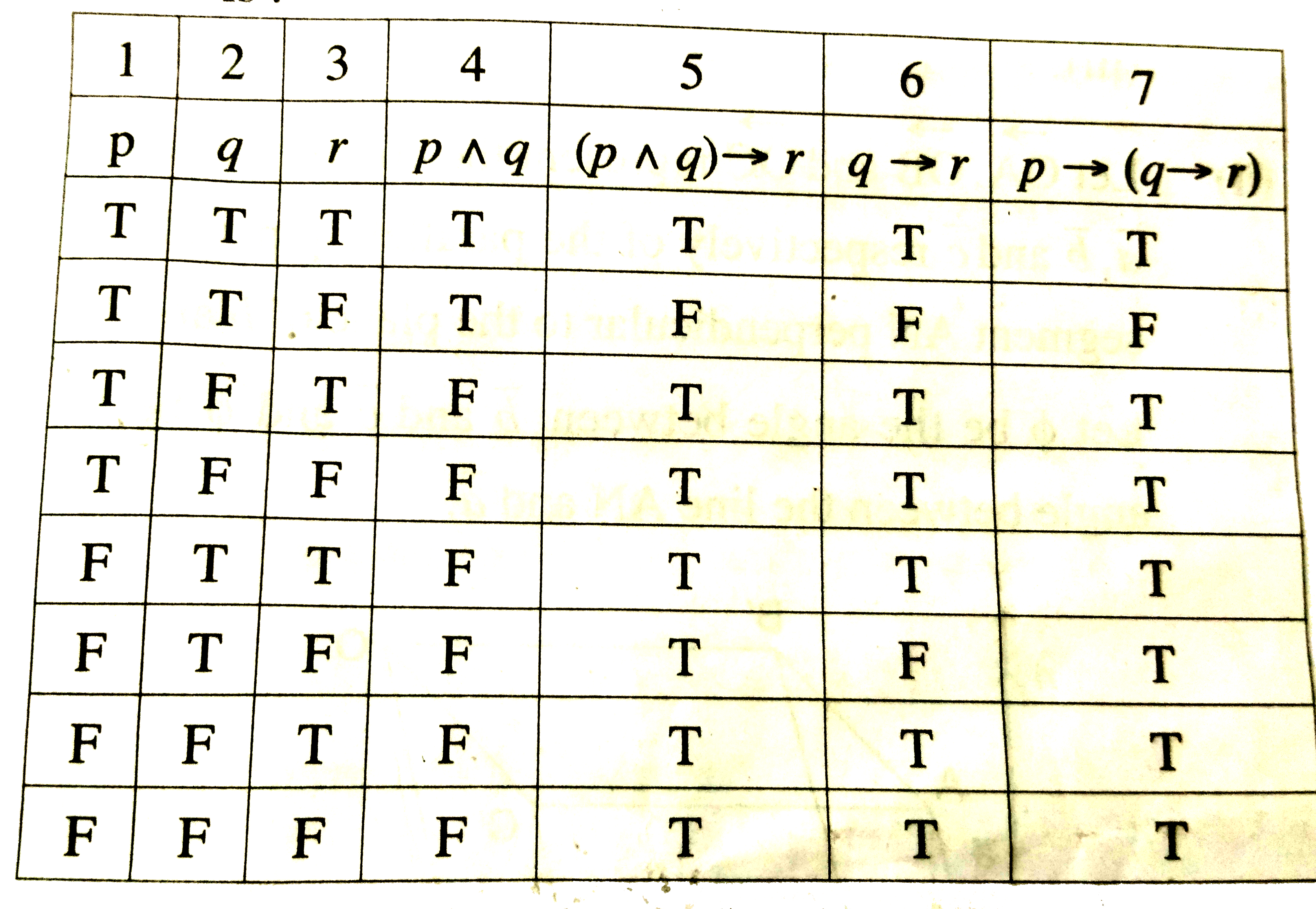
Zqbdlhvj0q3w2m

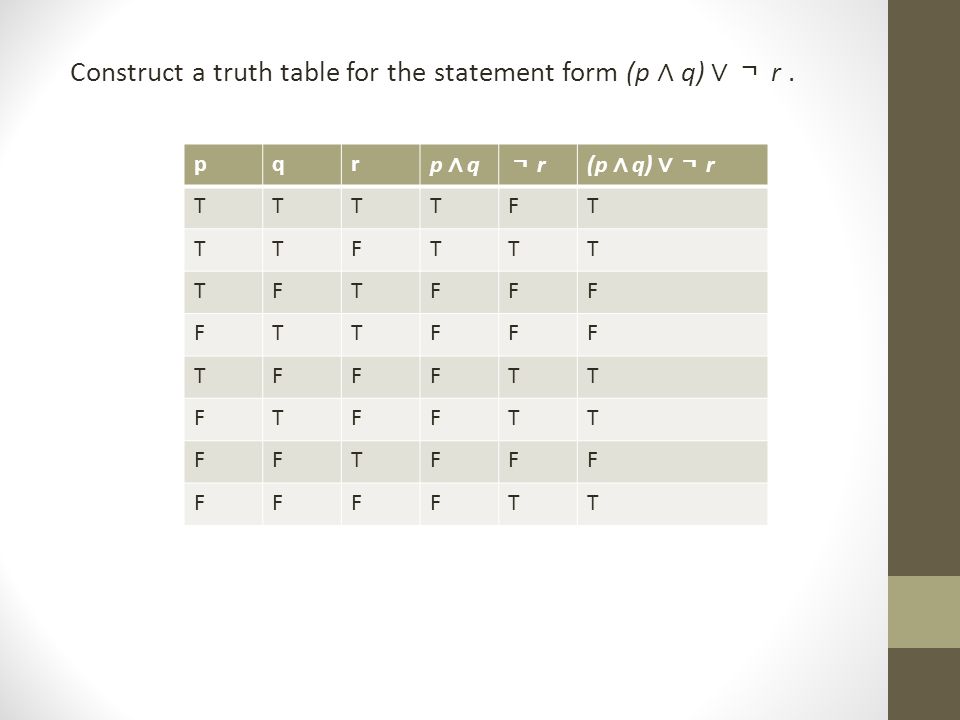
4i Complete The Truth Table Q Q P Q T T T Itprospt
Propositional Logic Dr Yasir Ali Formal Or Propositional Logic Was First Developed By The Ancient Greeks Who Wanted To Be Able To Reason Carefully Ppt Download
Biconditional
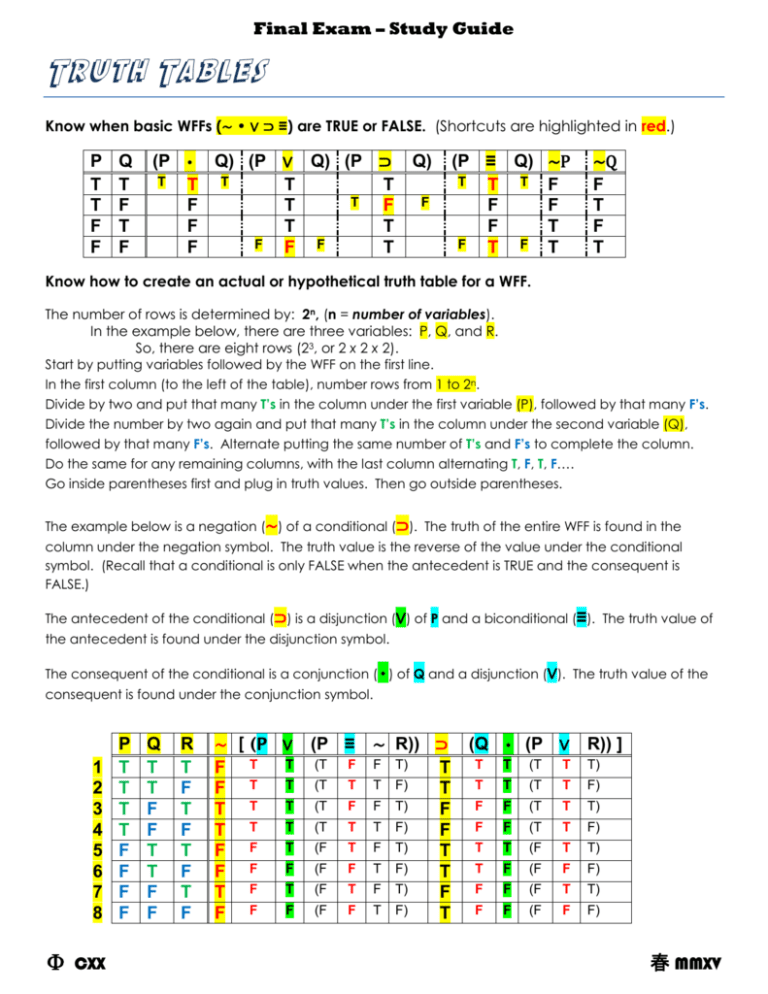
Truth Tables

What Is The Truth Table For This Logic Statement Stack Overflow
Solved The Compound Propositions P Q R And P Q R Are Not Logically Equivalent Because Course Hero

The Truth Table Represents Statements P Q And R Which Statement Is True For Rows A C And E R Brainly Com

Dm T
Discrete Mathematics Chapter 1 Logic And Proofs 1

Prove That Implication Is Transitive In The Propositional Calculus That Is That P Implies Q And Q Implies R Both Imply P Implies R Study Com

P Q R A S V T R V S A P V Q P Q P

Logic Truth Table For P Q R Q Youtube

Propositional Logic Truth Table Boolean Algebra Dyclassroom Have Fun Learning
Propositional Logic 1 Propositions A Propositionis A Declarative

Logic Truth Table For P Q R Q Youtube
Ans A P Q P V Q P P Q P V Q P
Gate 04 Logics Let P Q R S Be 4 Primitive Statements Consider These Arguments Gate Overflow
Logical Equivalence The Laws Of Logic In Mathematics It Is Important To Know Whether The Entities Being Studied Are Equal Or Whether They Are Essentially The Same For Example In Arithmetic And Algebra Two Nonzero Real Numbers Are Equal When They

Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange
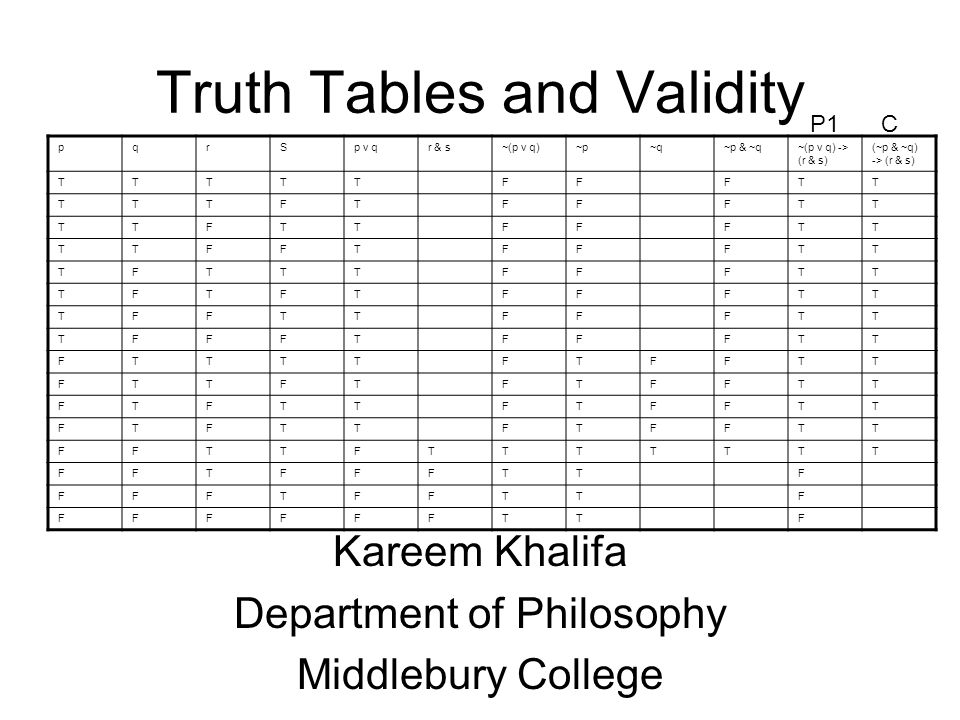
Truth Tables And Validity Kareem Khalifa Department Of Philosophy Middlebury College Pqrsp V Qr S P V Q P Q P Q P V Q R S P Q Ppt Download

3 2 Truth Tables And Equivalent Statements Ppt Video Online Download

Solved Problem 1 Consider Three Statements P Q R Statements 1 Using Truth Tables Recall The Proof Of The Logical Equivalence Betwccn P Q V R And P Q V P R This

Truth Tables Tautologies And Logical Equivalences

Solved Consider The Following Pair Of Statements In Which P Chegg Com

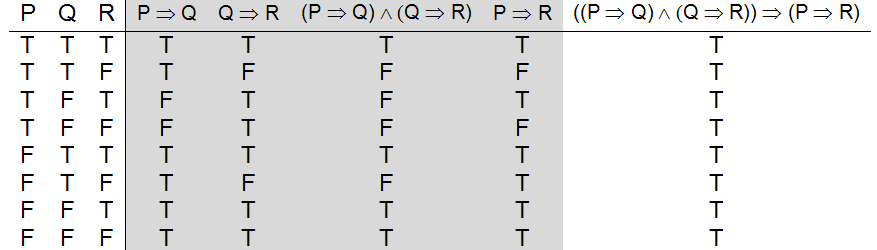
Construct The Truth Table For P Q R

Truth Table Generator 1 2 Free Download

Solved Q4 10 Points Suppose That The Statement P Q V R Rv S Is False Find The Truth Values Of P Q R And S This Can Be Done Without

2 Construct The Truth Tables For The Following Propositions 1 P P Q 2 P Q Q P 3 P Q R 4 P Q P R 3 Refer To The Propositions In Problem 2 For Each Of Them Indicate Whether It Study Com
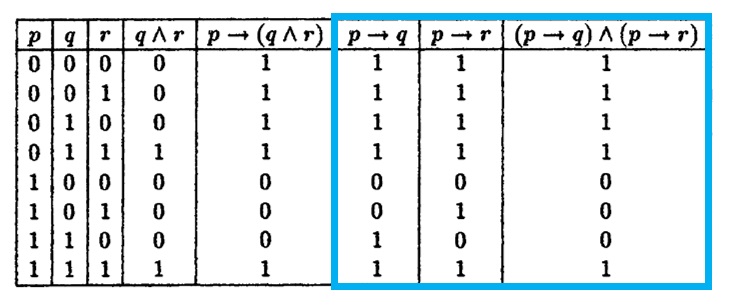
完了しました P Q Q R P R シモネタ

Solved 1 Use Truth Tables For The Following A Prove That P Q Paq B Find Truth Values For P Q Re Q Pvr C Give The Truth Table For P Q A R Q And Then Re Express That Statementjust Using

Truth Table For P Q R Youtube
1
Conjunction Truth Table
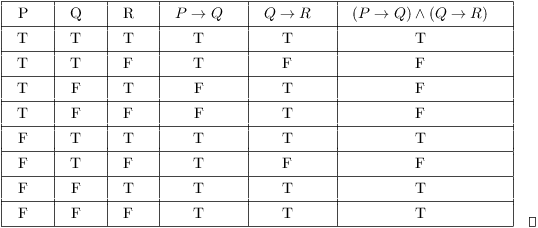
Truth Tables Tautologies And Logical Equivalences
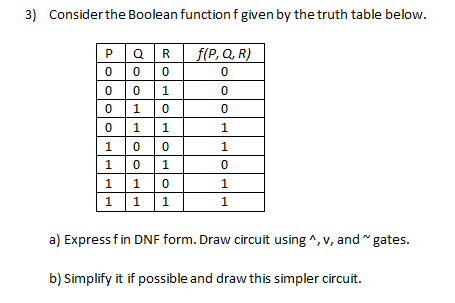
Solved 3 Consider The Boolean Function F Given By The Truth Chegg Com
Watson
Solved 1 A Student Sees The Following Problem And Completes The Truth Table Below Is The Following Set Of Sentences Satisfiable P Q R Course Hero

Using The Truth Table Prove The Following Logical Equivalence P Q P Q P Q
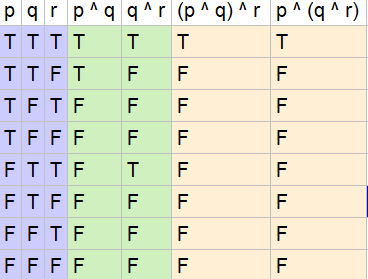
Use Truth Tables To Verify The Associative Laws A P Q Quizlet

Chapter 10 Truth Tables
How To Construct A Truth Table Of P Q P Quora

Truth Tables 1 4 Relations V 5 An Inference Over Download Scientific Diagram

Answered Consider The Following Truth Table Bartleby

Solution Let P Q And R Represent The Following Statements P Jamie Is On The Train Q Sylvia Is At The Park R Nigel Is In The Car Construct A Truth Table

Construct The Truth Table For The Compoundstatement Pwedge Q Vee R Snapsolve

Solved Use Truth Table To Verify That P Q P V Q P For Each Of The Following Say Whether It Is Equivalent To P 4 Q P Or Neither If
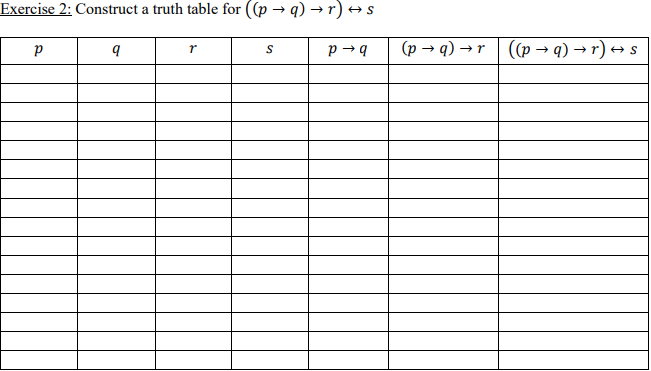
Solved Exercise 2 Construct A Truth Table For P Q R S R Chegg Com
Prove P Q R P Q R Without Using Truth Table Sarthaks Econnect Largest Online Education Community
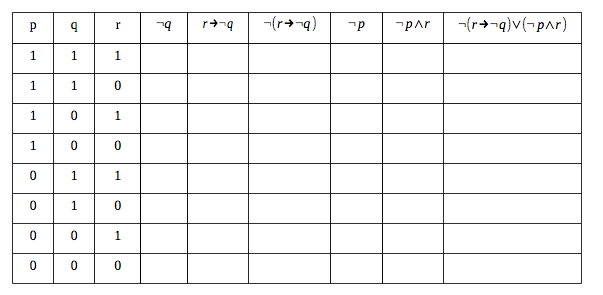
Solved P Q R Q R Q R Q P Par Chegg Com
Answer In Discrete Mathematics For Angelica Aguilar
Answer In Discrete Mathematics For Angelica Aguilar

Using A Truth Table To Prove Or Disprove P Vee Q Wedge R P Wedge Q Vee R And P Wedge Q Vee R P Vee Q Vee R Mathematics Stack Exchange

Review I Rosen 1 1 1 5 3




