三角形 辺の比 定理
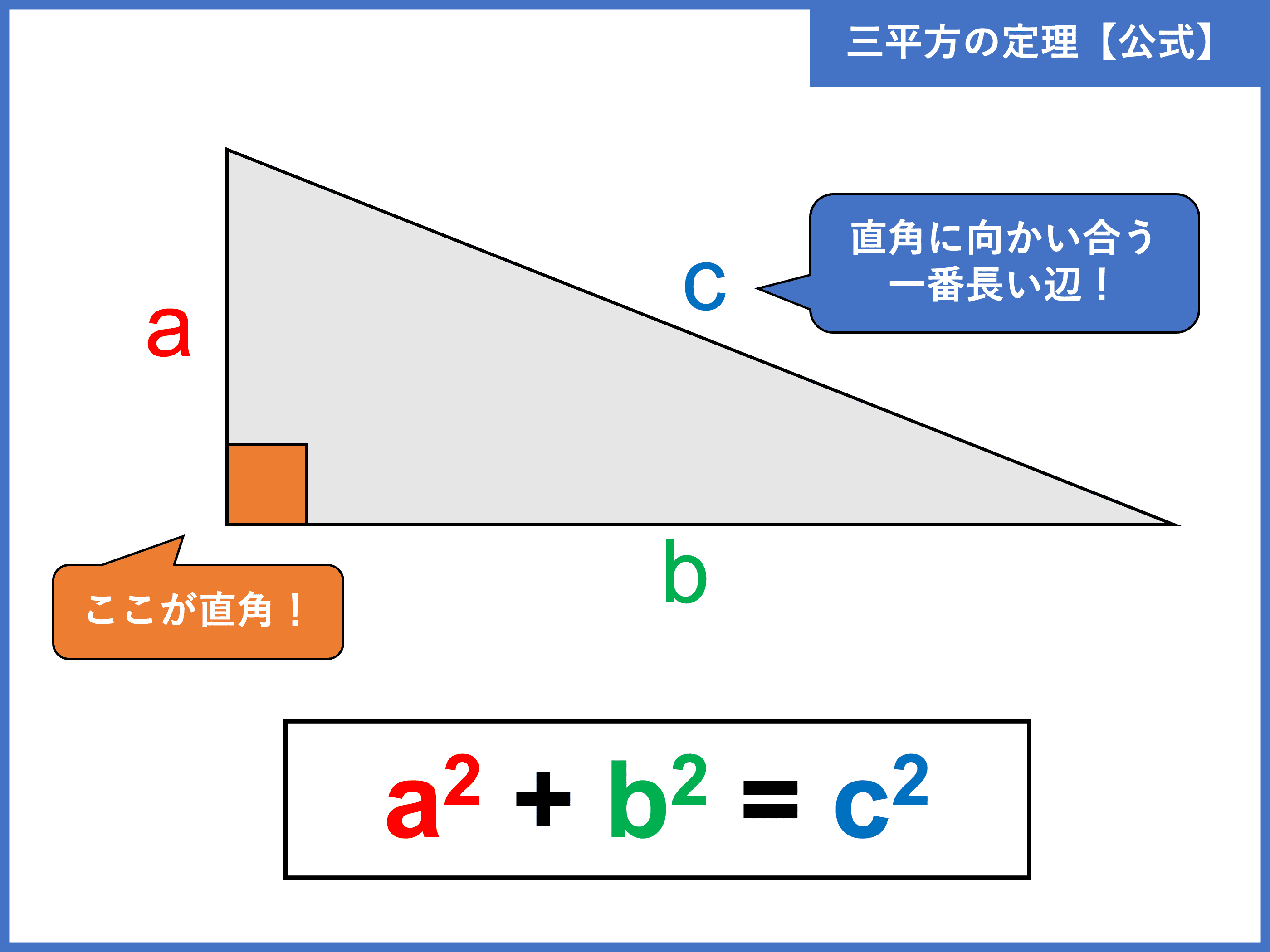
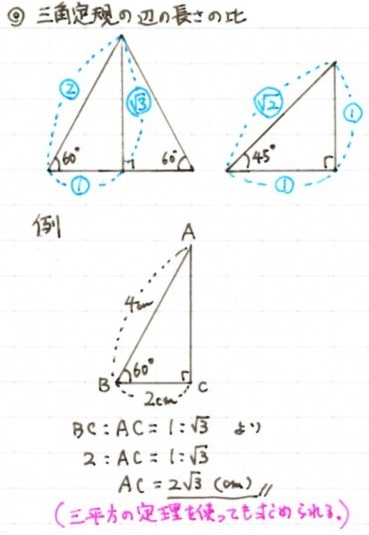
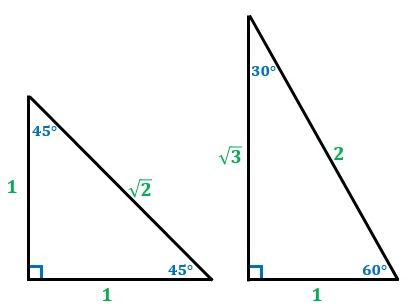
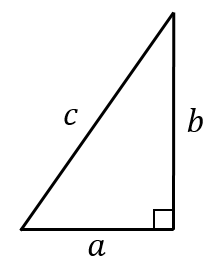
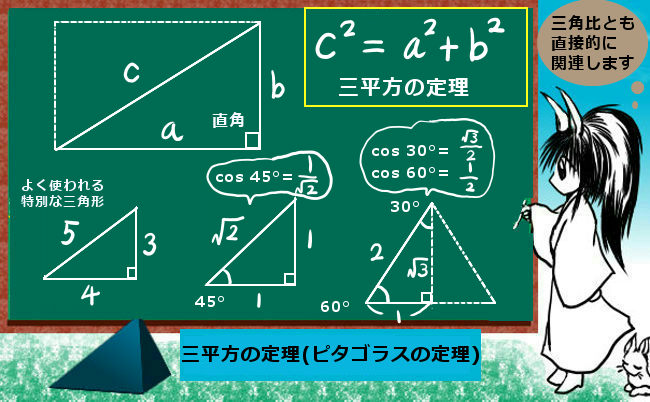
直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となります。 3辺の比は.

三角形 辺の比 定理. 次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。. 19/2/21 三平方の定理 直角三角形の直角を挟む \(2\) 辺の長さを \(a, b\) とし、斜辺を \(c\) とすると \begin{align}a^2 b^2 = c^2\end{align} 三平方の定理とは?証明や計算問題、角度と辺の比の一覧. 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。.
21/1/17 正方形から導かれる\( 45^\circ \)の三角比 次に、1辺の長さが1である正方形を利用して、\( 45^\circ \)の三角比を求めていきます。 以下の図のように、頂点B,Dを結び、対角線を引きます。 辺BDは、三平方の定理(ピタゴラスの定理)より. こちらは非常に有名な直角三角形です。 3つの辺の比が : : になっていれば、必ず直角三角形になります。 諸説ありますが、古代エジプトではこの形を使って直角を計り、ピラミッドを作ったのではないか、と言われているように昔から知られている形です。 整数だけで三平方の定理が成立する三辺の比のグループのことを、‟ピタゴラス数“といいます. 三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。.
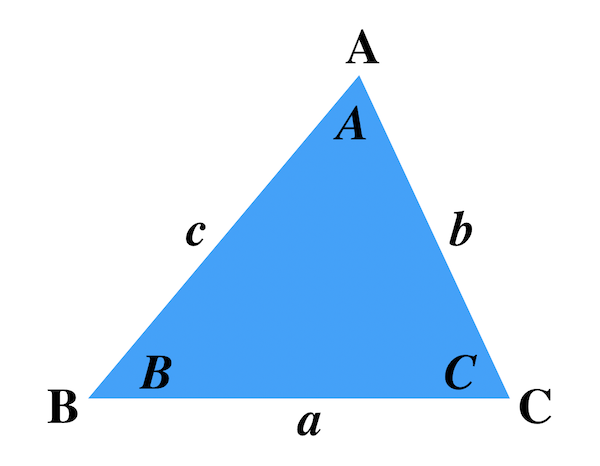
次に,メネラウスの定理を使って, abc の内部の線分の長さの比を求める. メネラウスの定理では,三角形と交わる直線の長さの比は出てこずに,直線によって分けられる三角形の辺の比が出てくる. 三角形の辺の長さや角の大きさを求めたいときは、正弦定理や余弦定理が有効ですが、その際、どちらを使えばよいのかは、確かに迷うところですね。 そこでまず、各々の定理について確認しておきましょう。 下の図のように3辺の長さが a , b , c で、辺に. $15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。.
11/1/17 三平方の定理では、特別な直角三角形辺の比を使って、三角形の辺の長さなどを求めることが出来ます。 基本事項をしっかり覚えて、素早く計算出来るように練習することが大切になります。 基本事項 次の3つの直角三角形の辺の比を覚えてください。. この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだ. 三角形の\(\,3\,\)辺の比が内角との比では無く、 対応する内角の 正弦との比に一致 するということです。 もう一つ注意点として描いておくと、 \(\hspace{10pt}ABC=180^{\circ}\) であることは忘れないようにしておきましょう。.
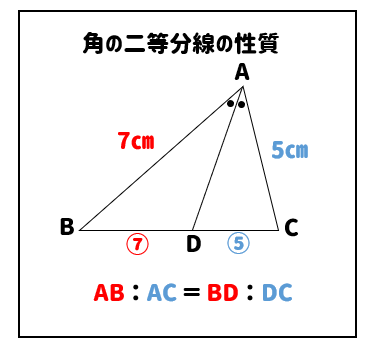
数学Aの平面図形で使う定理の一覧 三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 角の二等分線と辺の比の証明 三角形の外角の二等分線と辺の比 AB. 16/7/ 実は、 1つの角が等しい三角形の面積比は、その角をはさむ2辺の積によって求められます。 ABC: ADE=AB×AC:AD×AEと覚えておきましょう。 三角形の面積比のまとめ. 23/7/17 \(cd\) と \(ad\) の長さが分かったら、今度は右側の直角三角形 \(bcd\) に注目。 \(bcd\) は直角三角形なので、その3辺について三平方の定理 \(bc^2=cd^2db^2\) が成り立ちます。 ここに \(bc,cd,db\) の値を代入すると・・・.
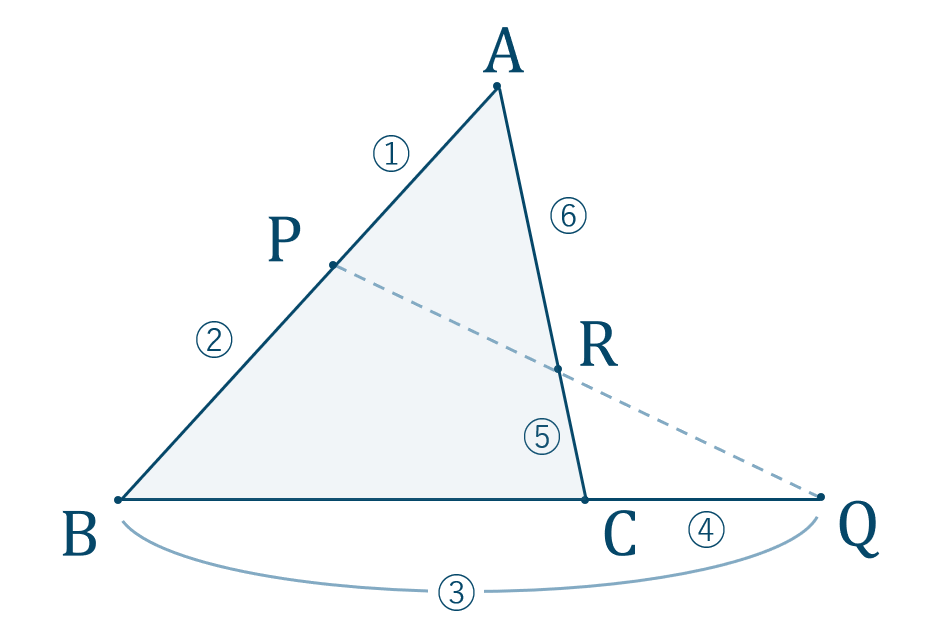
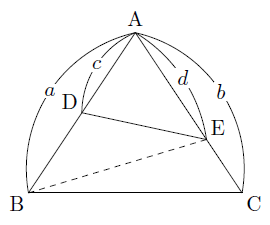
三角形と比の定理の逆 a b c d e abcの辺ab, ac上の点をそれぞれd, eとする。 ① adab=aeacなら de//bc となる。 ② addb=aeecなら de//bc となる。 定理の証明 ① adeと abcにおいて adab=aeac, ∠aは共通 よって2組の辺の比とその間の角がそれぞれ等しいので ade∽ abc. 正弦定理は、辺の比と sin sin の比が一致することを表している、と見ることもできるわけですね。 あとは、 標準余弦定理と比 と流れは同じです。 正の数 k を用いて、 a = 13k a = 13 k, b = 8k b = 8 k, c = 7k c = 7 k と書けます。 余弦定理から cosA = (8k)2 (7k)2 −(13k)2 2⋅ 8k⋅7k = 64 49 −169 2⋅8 ⋅7 = −56 2⋅8 ⋅7 = − 1 2 cos . メネラウスの定理とチェバの定理 メネラウスの定理 と チェバの定理 は、三角形の3辺について、 内分比や外分比によって得られる 比の値の積が1 になる定理 です。 式を覚えるのはコツがあるので、それほど苦労しません。.
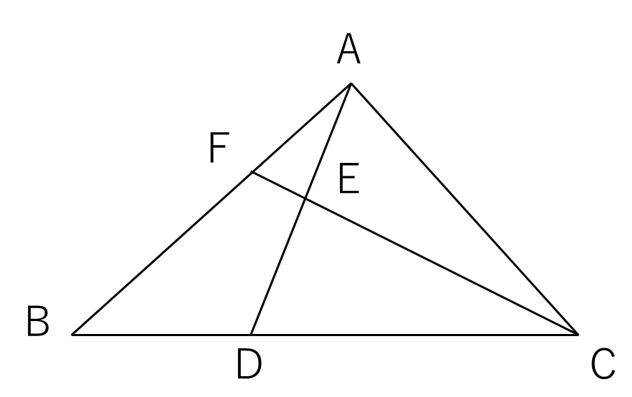
チェバの定理・メネラウスの定理 三角形ABCの辺BC,CA,AB上に点D,E,Fをとり、線分AD,BE,CFが1点Gで交わるとき、以下の等式が成り立つ。 チェバの定理の証明 図のように、a= BCG、b= CAG、c= ABG とします。. 19/2/21 直角三角形とは? 定義や定理、辺の長さの比、合同条件 21年2月19日 この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね! 目次 非表示 直角三角形の定義 直角三角形の定理(三平方の定理) 例題「斜辺の長さを求める」. 4 三角形の角と辺 ppooiinntt ama05 3 三平方の定理の応用(高校内容) c ab b a c c a b m ここでは,三平方の定理を利用して,三角形の辺の間に成り立つ関係について学習してみましょう。.
すなわち、√2とは、一辺の長さが1の正方形の対角線の長さになります。 もう一つの三角形の辺の比は、12 √3(内角は、90°、30°、60°) この場合、斜辺が2です。 1² √3² = 2² どちらも、三平方の定理が成り立ちます。. 26/7/21 比の値を意識することはなかったでしょうが、計算の中に 比の値 、つまり 三角比 が登場していたことは確かです。 ここから分かることは、 相似の関係にある直角三角形の辺の長さは、 比の値 を使えば求めることができる ということです。 察しの良い人なら、三角比から得られるメリット. 12/7/19 三角形の角の2等分線と比例 三角形の内角、外角の二等分線での内分点、外分点の関係性 で およびその外角の二等分線が直線AB上に交わる点をM、Nとすると となり、逆も成り立つ。 また上の式が成り立つとき、 、 は を調和に分けるといい.
2/4/19 また、三角形の外部を直線が通るときは、その直線と3辺の延長線分との交点で外分するが、その3つの比の値の積もまた-1になる。 最後に、きちんとまとめ直せば、以下の通りである。 チェバの定理 (1)三角形の内部に点がある場合. 三角形と比の定理の逆の証明 三角形と比の定理の逆の証明 ABCの辺AB,AC上にそれぞれ点P,Qがあるとき、次のことが成り立つことを証明せよ。 APPB=AQQCならばPQ∥BC 宜しくお願いします。 もし相似を使うなら、相似条件もはしょらずに書いてください。. 三角比 三角比とは、 三角形の各辺の長さを用いた比 のことを指します。 ただ、辺の比と言われてもピンとこないので実際に文字で置いて解説していきます。 三角比の公式 三角比は\(sin\)(サイン)や\(cos\)(コサイン)という記号を使って表現します。.
三平方の定理_特別な直角三角形 特別な直角三角形とは 三角定規になっている直角二等辺三角形と、正三角形を半分にした三角形は角度がそれぞれ 45°, 45°, 90° と 30°, 60°, 90°となり、3辺の長さの比が次のようになる。. 直角三角形の底辺、斜辺の求め方など下記が参考になります。 直角三角形の底辺の長さは?1分でわかる計算、斜辺、高さ、角度 直角二等辺三角形の辺の長さは?1分でわかる求め方、公式 三角比を使えば辺の長さの比を用いて三角形の角度を表すことが. 3/7/17 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。.
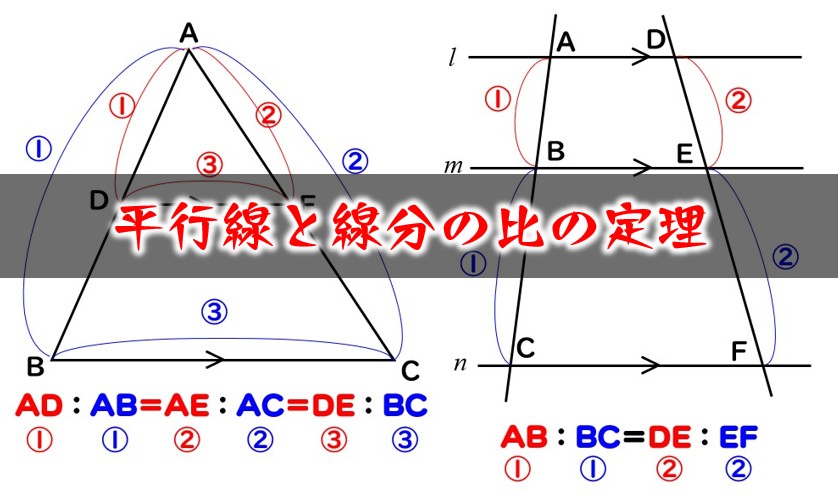
平行線と線分の比の定理 の問題の解き方 数学fun

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
三角形 辺の比 定理 のギャラリー

無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局
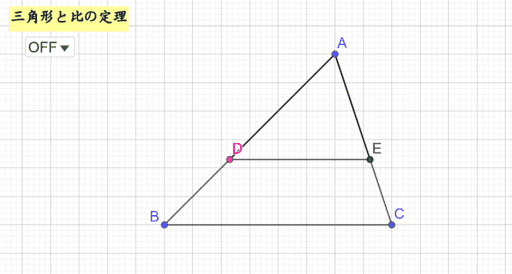
三角形と比の定理 Geogebra

直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える

平面図形をマスター 三角形の面積比 応用編その3

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
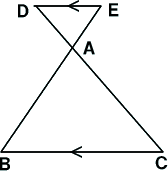
三角形と比

三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト
1
直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

三平方の定理の証明と使い方
M 2 三角形の辺の比を求める 2 Solid Line

数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ

3 4 5の三角形で 本当に直角ができる Note Board
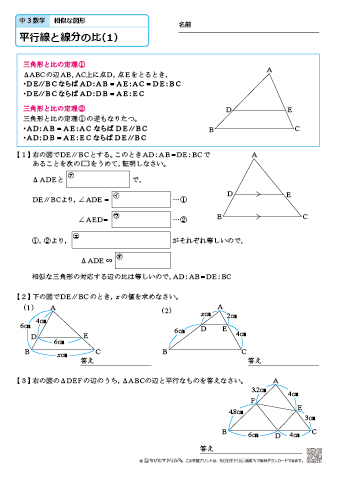
中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

角の二等分線の性質と二等分線の長さ 思考力を鍛える数学

特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座

数学 中3 61 三平方の定理 基本編 Youtube
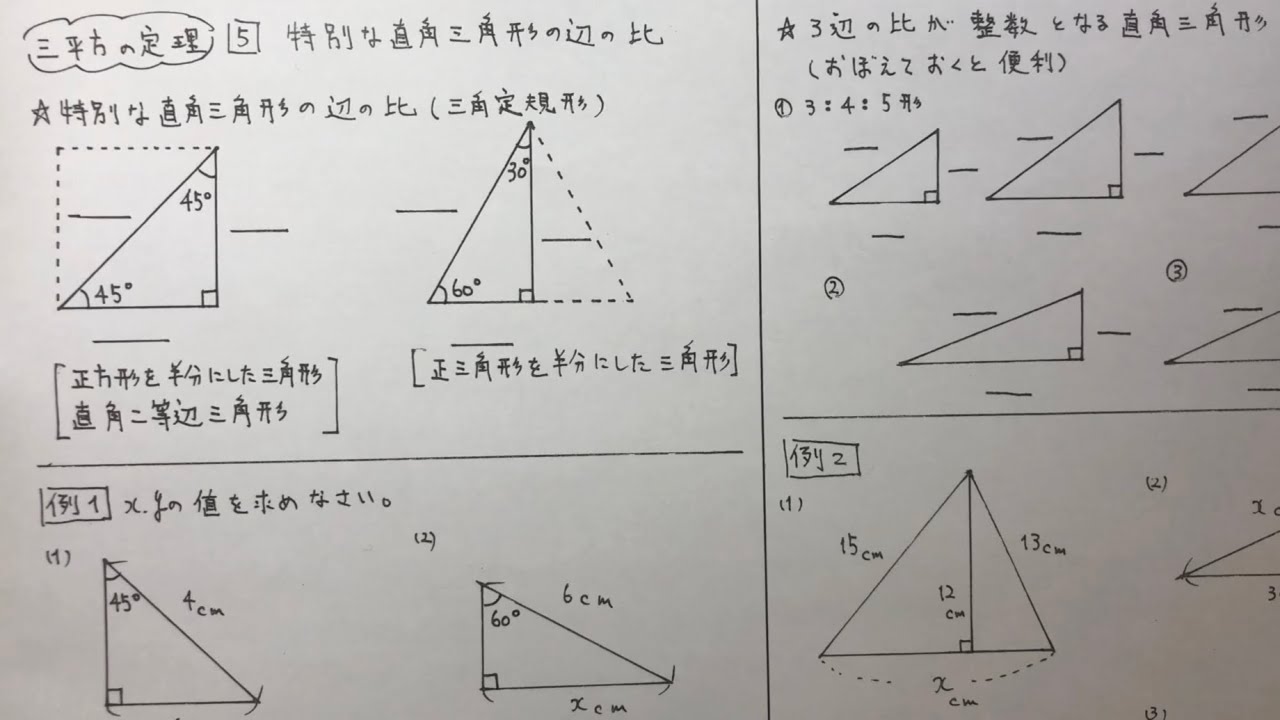
中3数学 三平方の定理5 特別な直角三角形の辺の比 Youtube

面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
直角三角形の3辺の比 高校入試問題 数学 を毎日解いてみよう

余弦定理で角度を求める方法 数学の星

角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ

平行線と線分の比の定理 の問題の解き方 数学fun

サクッと解説 角の二等分線と比の特徴となぜ について 数スタ

苦手を克服 数学aの平面図形で使う定理の一覧 数学a By となりがトトロ マナペディア

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

平面図形をマスター 三角形の面積比 応用編その3

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題
三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba
公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学

高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月
直角三角形の辺の比 東久留米 学習塾 塾長ブログ

数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ

平面図形をマスター 三角形の面積比 応用編その3

特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてく Clearnote

3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

Newみんなの算数講座86 三角形を全部見てはいけない 中学受験の算数知恵宝庫

三角比は直角三角形が基本 理系男子の独り善がり

数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学

高校数学a チェバの定理とメネラウスの定理の基本問題演習 受験の月

中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

余弦定理 は三平方の定理の進化版 余弦定理は2つある
1角共有の三角形の面積比 まなびの学園
1

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

数学 中3 49 平行線と線分の比 基本編 Youtube
三角形の面積比をてんびんで解く 中学受験プロ講師ブログ

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
平行線と線分の比

数学 中3 51 平行線と線分の比 中点連結定理編 Youtube
中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座

平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

平面図形をマスター 三角形の面積比 応用編その3

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
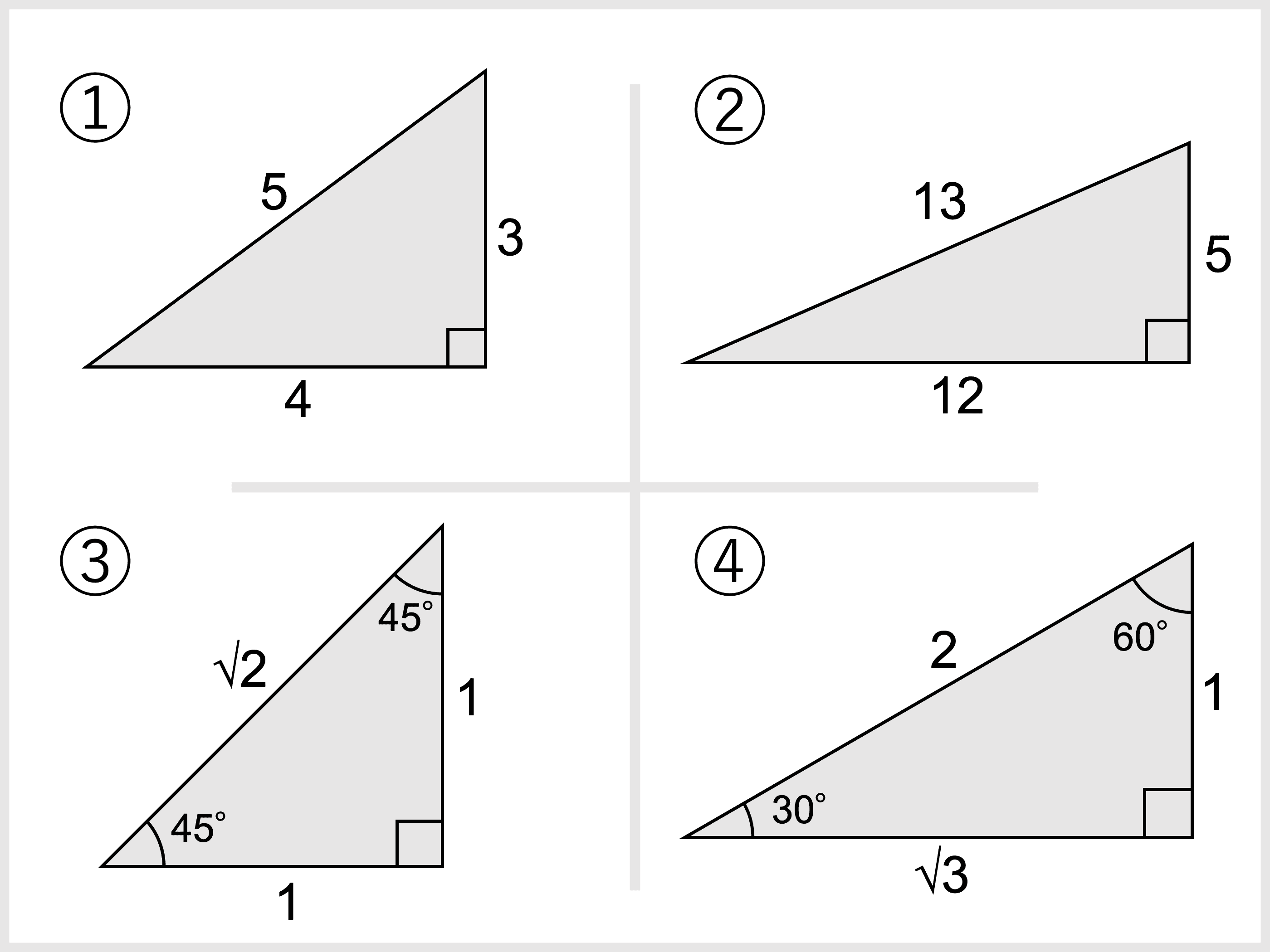
直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
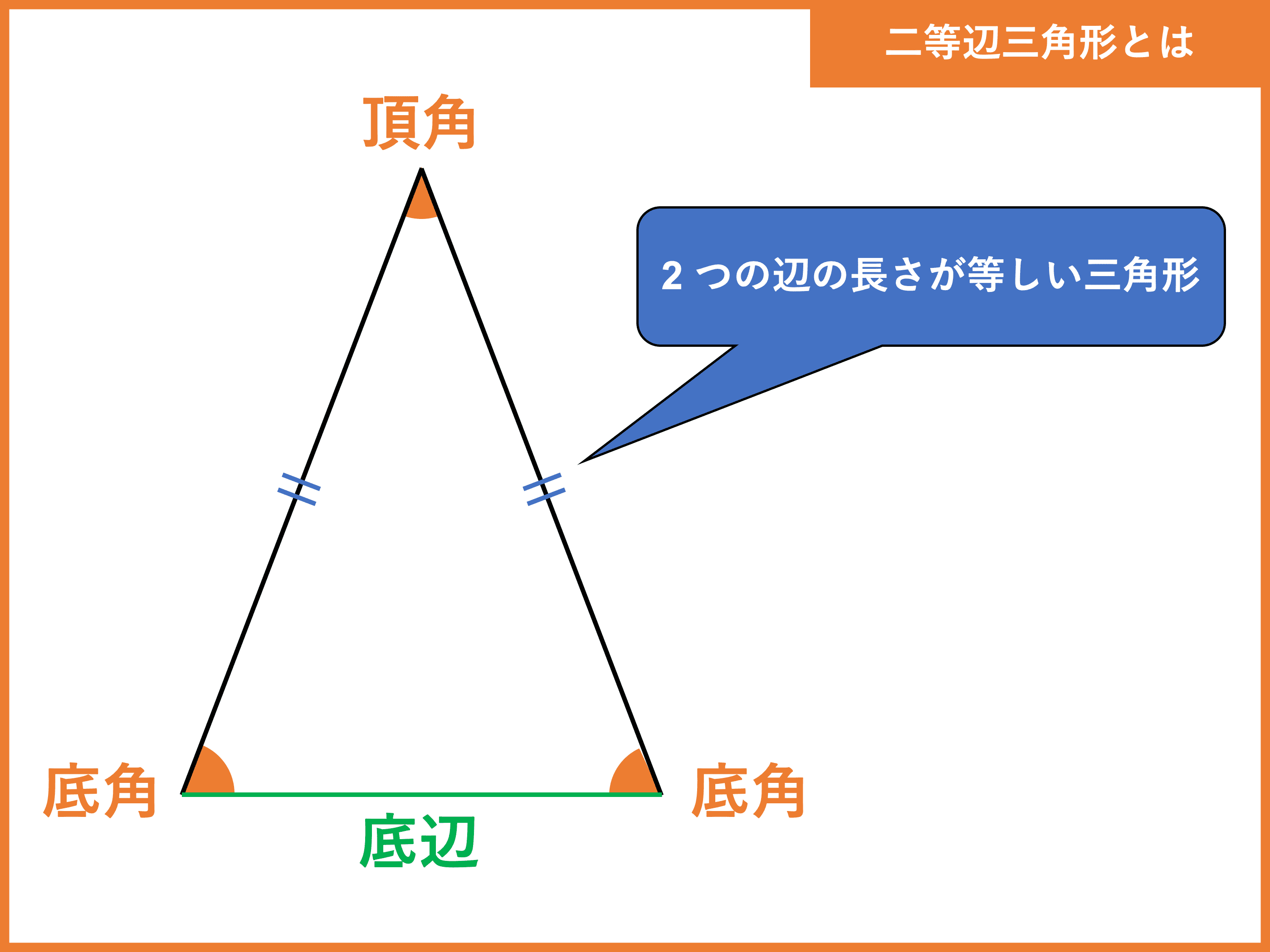
二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典

中3 三角形と比の定理の逆 中学生 数学のノート Clearnote
直角三角形の辺の比の関係 Sin Cos Tan 理数系無料オンライン学習 Kori

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
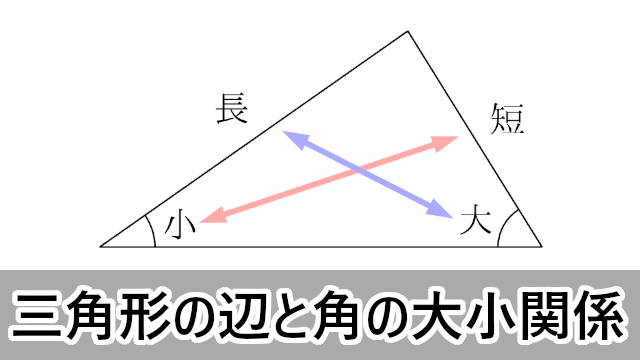
数学ia 三角形の角の大きさと辺の長さの関係 証明 大学入試数学の考え方と解法

三平方の定理と二等辺三角形 Youtube
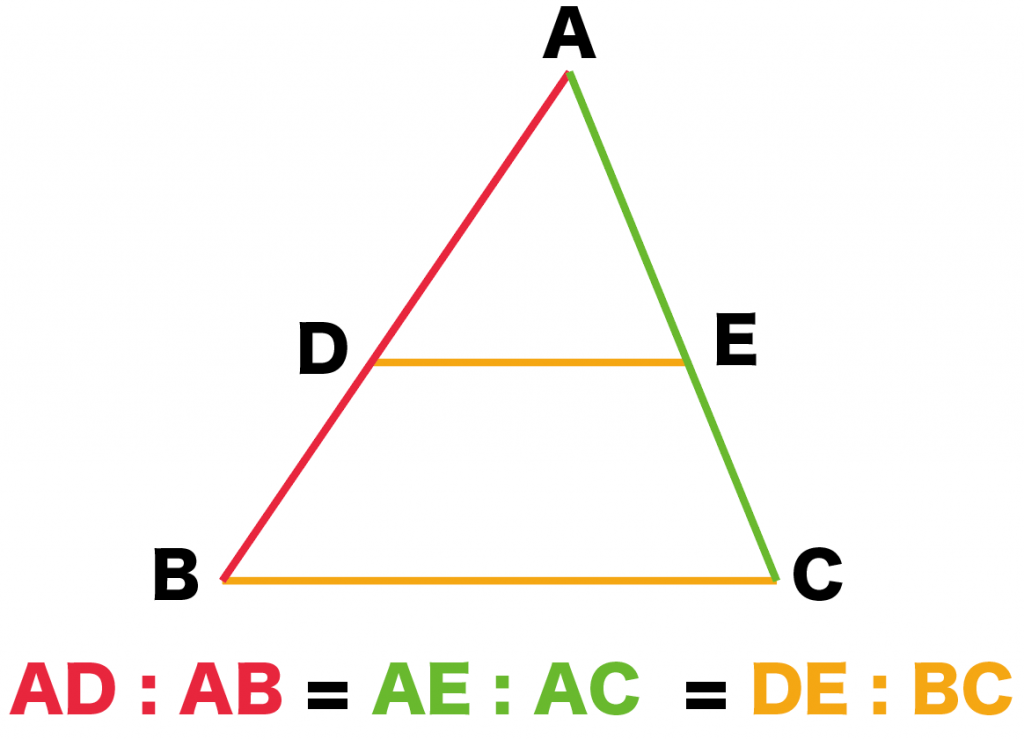
3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく

辺の比と面積比 基本編 Youtube
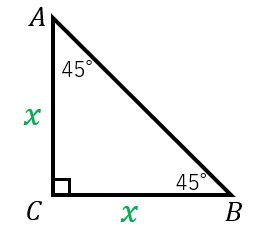
30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

黄金三角形による18 シリーズの三角比 おいしい数学
1
1
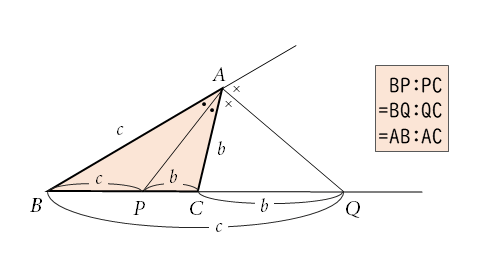
数学の公式 定理集 図形の性質 日々是鍛錬 ひびこれたんれん

中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似




