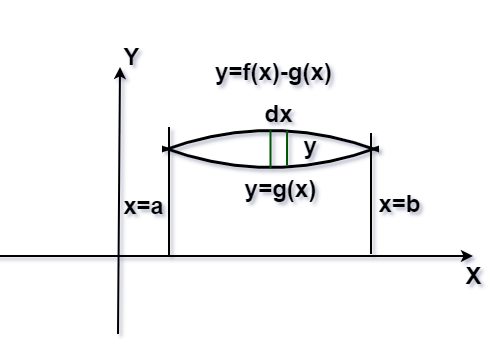
Consider The Parabola Yx2 The Shaded Area Is
between y = 4x − x2 and y = x then subtract from the integral of the first (between a and b) the integral of the second (again, between a and b) Part 1 Points of intersection occurs when 4x −x2 = x This occurs when either x = 0 or x = 3 (we could, but don't actually need to calculate ya and yb).
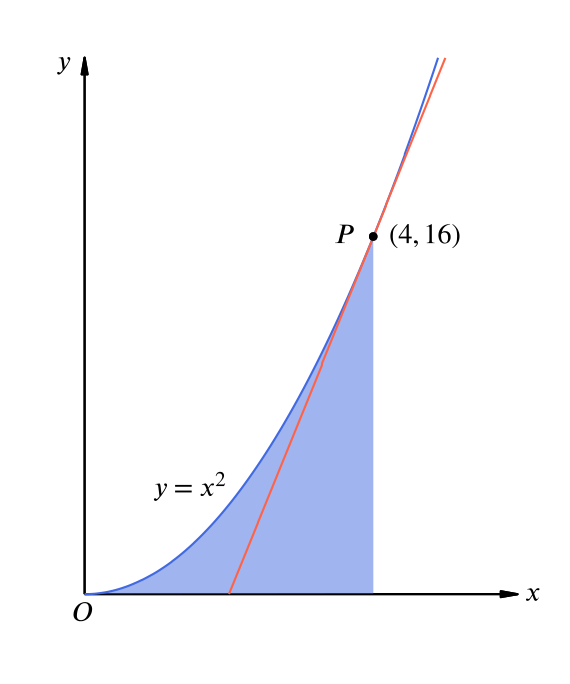
Consider the parabola yx2 the shaded area is. 4E6 Consider the parabola y = x2 Find the parametrization using the slope of the curve at a point (x,y) as the parameter 4E7 Find the parametrization of the circle x 2y = a2 using the slope as the parameter Which portion of the circle do you obtain in this way?. Question 10 What will be the area in the first quadrant bounded by the parabola, y = x 2 1, the tangent to it at the point (2, 5) and the coordinate axes Solution The equation of tangent is (y 5)/2 = 2x 1 => y 5 = 4x 2 or y = 4x – 3 Required area =. Area y=x^21, (0, 1) \square!.
Math Calculus Calculus questions and answers Consider the region bounded by the line y = 2x and the parabola y = x^2 Set up, but do not evaluate the integral (or integrals) you would use to find the volume of the solid obtained by revolving this region about the xaxis Consider the region bounded by the parabola y = x x^2 and y = 0. Of the integral cancel, so each xintegral is 0, hence the entire area integral is 0 Problem 2 () Use symmetry to evaluate ZZ R sinxdAfor R= 0;2ˇ 0;2ˇ Solution For each y, the xintegral is the integral of sinxover a whole period, so is 0 Thus the entire area integral is 0 Problem 3 () Evaluate Z 1 1 Z ˇ 0 x2. Answer (1 of 3) Shaded Area in the attached diagram = Integral from 0 to 1 of 2(√(2x x²) √x) = π/2 4/3 The required area = π π/2 4/3 = π/2 4/3.
Find the area of shaded region bounded by parabola y=x^2 and the line y= x2 Find the area of region bounded by x =4y^2 and y axis Find the area between the curve y=cosx and x axis on the interval 0,π Find the area between lines y=x and y=1 and curve y =x^2 /4 in the first quadrant Answers 9/2 units;. Misc 6 Find the area enclosed between the parabola 𝑦2=4𝑎𝑥 and the line 𝑦=𝑚𝑥 Let’s first draw the Figure Here, 𝑦2 =4ax is a Parabola And, 𝑦=𝑚𝑥 is a straight line Let A be point of intersection of line and parabola Finding point A Putting y = mx in equation of parabola 𝑦^2=4𝑎𝑥 (𝑚𝑥)^2=4𝑎𝑥 𝑚^2. Application of integrals 2Find the area between the curves y = x and y = x^2ncert solutions class 12 maths,ncert solution of class 12 maths,maths ncert sol.
Consider the parabola y 2 = 8 x Let Δ 1 be the area of the triangle formed by the end points of its latus rectum and the point P (2 1 , 2) on the parabola, and Δ 2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum Then Δ 2 Δ 1 is. 2dxdy=2(area ofD)=2 a2 The rightmost expression is twice the area of a disk of radiusa In this case, the double integral is much easier to consider than the line integral The use of GreenÕs theorem in Example 2 can be put in a much more general setting Indeed, if D is any region to which GreenÕs theorem can be applied, then,. 8 π 2 8\pi\sqrt {2} 8π 2 16 π.
1What is the area bounded by the curves y= x2 1 and y= 2x 7?. 6 Chapter 6 Applications of the Integral 28 Figure 16 Figure for Problem 28 29 x = y2 — 5 x = 3 — y2 Figure 17 Figure for Problem 29 We have 2 − 2 3 − y2 − y2 −5 dy= 2 −2 8 −2y2 dy= 8y − 2 3 y3 − = 30 Figure 18 shows the graphs of x = y3 −26y 10 and x = 40 −6y2 − y3Match the equations with the curve and compute the area of the shaded region. Consider another example when we have a parabola Example Find the area of the region bounded by the curve y=x 2 and the line y=2 Solution For the above case, we would get the following figure, From the given figure, we can see that the parabola is symmetric about the yaxis.
Area Under a Parabola Consider a parabolic arch (similar to the St Louis arch, which is not a parabola, but a catenary) with the width of its base B and height H We want to find a formula for the area under the arch. Consider the parabola y 2 =8x Let Δ 1 be the area of the triangle formed by the end points of its latus rectum and the point P(1/2,2) on the parabola, and Δ 2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum Then Δ 1 /Δ 2 is. Find the area of the shaded region 3) f(x) = x 3 x 2 6x g(x) = 6x 3) 4) y = x 2 2x y = x 4 4) Find the volume of the described solid 5) The solid lies between planes perpendicular to the x axis at x = 4 and x = 4 The cross sections perpendicular to the x axis are circular disks whose diameters run from the.
Ii calculate the shaded area enclosed by the parabola (ii) Calculate the shaded area enclosed by the parabola and the line 3 (c) Consider the function x y 2 x 2 1 0 1 y (i) Copy and complete the table above 2 1 (ii) Using Simpson's Rule for five function values, find an estimate for the area shaded in the diagram below 3 O y x A 0 y x 2. So the curves intersect when x= 4 and x= 2. Answer As we can see in the gure, the line y= 2x 7 lies above the parabola y= x2 1 in the region we care about Also, the points of intersection occur when 2x 7 = x2 1 or, equivalently, when 0 = x2 2x 8 = (x 4)(x 2);.
Then we can determine the area of each region by integrating the difference of the larger and the smaller function Area in Polar Coordinates Consider the region \(OKM\) bounded by a polar curve \(r = f\left( \theta \right)\) and two semistraight lines \(\theta =\alpha\) and \(\theta = \beta\) Figure 3 The area of the polar region is given by. Solution for Consider the infinite sequence of shaded right triangles in the accompanying diagram Compute the total area of the triangles 1 l00 0 IN IN Problem 10 The volume of the solid obtained by rotating the region bounded by y=(x^2), If lines are drawn parallel to the coordinate axes through a point P on the parabola y². 60,912 11,296 intelli said Find c>0 such that the area of the region enclosed by the parabolas y= x^2c^2 and y = c^2x^2 is 110 what is value of c i got 349 and it is wrong i dont understand how to do this problem any help would be greatly appreciated How did you get 349?.
Consider the parabola y=x^2 The shaded area is Consider the parabola y= x2 x 2. Show us your work please. Area of ellipse is `pi` ab Area of shaded refion = Area of ellipse Area of rectangle `=pi ab 2ab = ab (pi2)` ← Prev Question Next Question → Find MCQs & Mock Test Consider the parabola `y=x^(2)7x2` and the straight line `y=3x3` The equation of the ellipse whose centre is at origin, major axis is along xaxis.
View LECTURE 5pdf from MATHS 144 at University of Zambia Application of integration Area under a curve Consider the shaded areas ∗ , ∗ , ∗ and ∗ below = • = () =. Finding the Area of a Complex Region Consider the region depicted in Figure 67 Find the area of R R Figure 67 Two integrals are required to calculate the area of this region Solution As with Example 63, we need to divide the interval into two pieces. Find the area of the region bounded by y 2 = 9x, x = 2, x = 4 and the xaxis in the first quadrant The equation of curve is y 2 = 9x, which is right handed parabola Two lines are x = 2, x = 4.
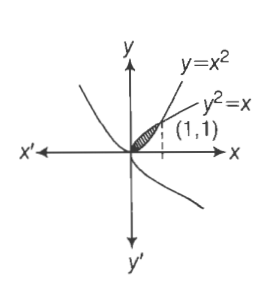
Find the area bounded by the following curves y x2 4, y 0, x 4, Graph b Finding the boundaries and y 00 implies x2 4 0 so x 2 x 2 or x 2 From the graph we see that is our boundary at a The value is a solution to the equation above but it is not bounding the area (Here ’s why the graph is an important tool to help. Find the volume of the solid generated by revolving the shaded region about the xaxis 14 CavalieriÕs principle A solid lies between planes perpendicular to the xaxis at x =0 and x = 12 The crosssections by planes perpendicular to the xaxis are circular disks whose diameters run from the line y = x>2 to the line y = x as shown in the accom. Consider the following figure Find the point of intersection (P) of the given parabola and the line (2) Find the area of the shaded region (2) Answer 1 We have, y = x 2 and y = x ⇒ x = x 2 ⇒ ⇒ x 2 – x = 0 ⇒ x(x – 1) = 0 ⇒ x = 0, 1 When x = 0, y =0 and x = 1, y = 1 Therefore the points of intersections are (0, 0) and(1, 1) 2.
Find the area enclosed between the curve x 2 = 4y and the line x = 4y – 2 (March 11) Answer Question 3 (i) Area of the shaded portion in the figure is equal to (ii) Consider the curves y = x 2, x = 0, y = 1, y = 4 Draw a rough sketch and shade the region bounded by these curves, Find area of the shaded region Answer Question 4. 4E8 At noon, a snail starts at the center of an open clock face. Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!.
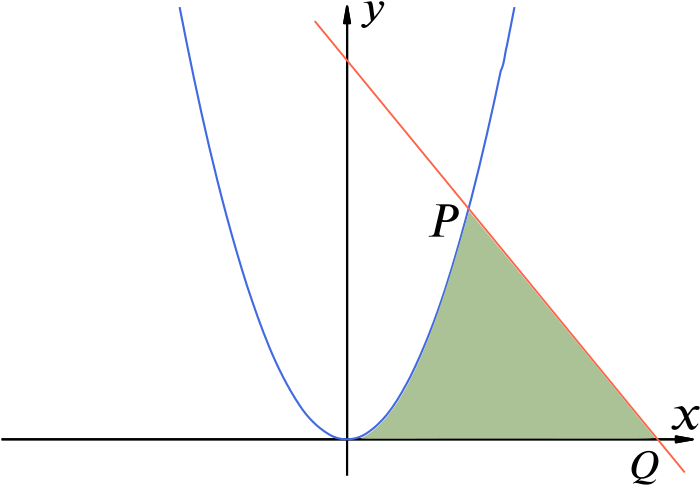
Conic Sections Level 3 Challenges The figure above shows two ellipses whose major axes are perpendicular to each other Each ellipse passes through the other ellipse’s foci, which form the vertices of a square If the shaded square encloses an area of 16, then what is the area enclosed by one of the ellipses?. The area of the region between the curves is defined as the integral of the upper curve minus the integral of the lower curve over each region The regions are determined by the intersection points of the curves This can be done algebraically or graphically. Example 1 Determine the area of the region enclosed by \(y = {x^2}\) and \(y = \sqrt x \) where the “” gives the upper portion of the parabola and the “” gives the lower portion Here is a sketch of the complete area with each region shaded that we’d need if.
The regions are determined by the intersection points of the curves This can be done algebraically or graphically Area = ∫ 3 0 −y2 2ydy−∫ 3 0 y2 −4ydy A r e a = ∫ 0 3 y 2 2 y d y ∫ 0 3 y 2 4 y d y Integrate to find the area between 0 0 and 3 3. Transcript Ex 81, 9 Find the area of the region bounded by the parabola = 2 and = We know = & ,. Answer (1 of 2) At the point of intersection with the x axis, y=0 9x^2=0 \implies x=\pm 3 The parabola is symmetric on x=0 So 2\displaystyle \int_{0}^{3} 9–x^2 \,dx =2\left9x\dfrac{1}{3}x^3\right_{0}^{3} =29(3)9 =2\times 18 =36.
Y=x2 (1,1) (4,2) Figure 2 The area between x = y2 and y = x − 2 split into two subregions If we slice the region between the two curves this way, we need to consider two different regions Where x > 1, the region’s lower bound is the straight line For x < 1, however, the region’s lower bound is the lower half of the sideways parabola. AREA In chapter 4, we introduced integration in terms of area between the curve and the xaxis This chapter, we will discuss area between two curves and methods Also, we will talk about integral and derivative properties in terms of their graphs AREA BETWEEN TWO CURVES The area between two curves is really simple if you really look at it Lets consider f(x)=6x2. Consider the following figure Find the point of intersection (P) of the given parabola and the line (2) Find the area of the shaded region (2) Answer 1 We have, y = x 2 and y = x ⇒ x = x 2 ⇒ ⇒ x 2 – x = 0 ⇒ x(x – 1) = 0 ⇒ x = 0, 1 When x = 0, y =0 and x = 1, y = 1 Therefore the points of intersections are (0, 0) and(1, 1) 2.
Required area (shaded area) = Area under ellipse from x = 0 to x = 3)(Area under line from x = 0 to x = 3) OR Required area (Shaded) = Area of ellipse in 1st quadrant – Area of Δ ABC Question 10 Find the area of the region enclosed by the parabola x 2 = y, the line y = x 2 and the x – axis Ans x 2 = y is an upward parabola line y = x 2. Find the area of the following regions, expressing your results in terms of the positive integer n ≥ 2 Let A n be the area of the region bounded by f ( x) = x 1 / n and g ( x) = x n on the interval 0, 1, where n is a positive integer Evaluate lim h → ∞ A n and interpret the result Caelan T. The formula for finding this area is, A= ∫ β α 1 2r2dθ A = ∫ α β 1 2 r 2 d θ Notice that we use r r in the integral instead of f (θ) f ( θ) so make sure and substitute accordingly when doing the integral Let’s take a look at an example Example 1 Determine the area of the inner loop of r = 2 4cosθ r = 2 4 cos .
9 Find the area of the region bounded by the parabola y = x^2 and y= xarea of region bounded,area of a bounded region,area of the region bounded by the gr. Consider the region S that lies between two curves y = f(x) In the figure given below, the equation of the solid parabola is y = x 2 3 and the equation of the dashed line is y = 2x Determine the area of the shaded region Solution Let us find the point of intersection,. A= 32/27 Consider the function f(x) = (x^22x4) (2x^24x3) f(x) = 3x^22x1 The values of x for which the two curves intersect are the solutions of the equation f(x) = 0 3x^22x1=0 x= (1sqrt(13))/3 x_1 = 1/3, x_2=1 Note now that as f(x) is a second degree polynomial with leading positive coefficient, its value is negative in the interval between the roots The area.
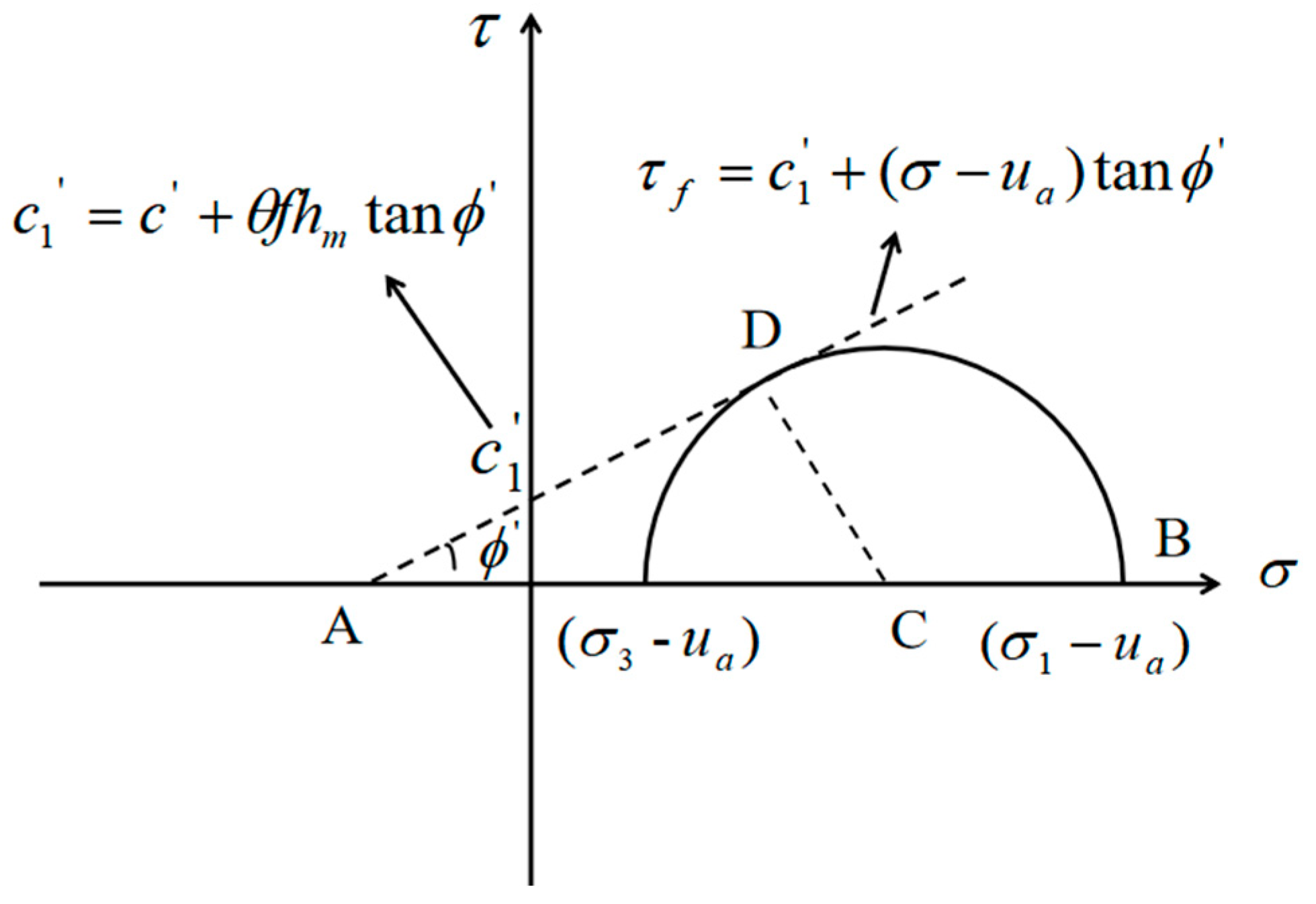
Materials Free Full Text An Improved Mechanistic Empirical Creep Model For Unsaturated Soft And Stabilized Soils Html

Solve This 10 Consider The Parabola Y X2 The Shaded Area Is 1 232 533 734 Physics Motion In A Straight Line Meritnation Com
Answer In Calculus For Prathamesh
Consider The Parabola Yx2 The Shaded Area Is のギャラリー

Consider The Parabola Y X 2 The Shaded Area Is

Quadratic Systems A Line And A Parabola Video Khan Academy
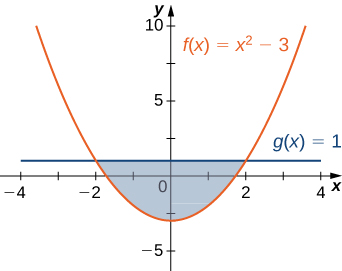
6 1 Areas Between Curves Calculus Volume 1
Math Emory Edu

Consider The Parabola Y X 2 The Shaded Area Is
Stewartcalculus Com

Solved Determine The X And Y Coordinates Of The Centroid Of The Shaded Area Assumec 6 A 1 10 6 215 X3 Y L 7 Answer Y In

Consider The Parabola Y X 2 The Shaded Area Is Brainly In

Mechanics Map Centroid Of An Area

Question Video Finding The Area Of A Region Bounded By Two Quadratic Functions Nagwa
People Wku Edu

7 07 Compound Areas And The Area Between Two Curves Lesson Mathspace
Wssd K12 Pa Us

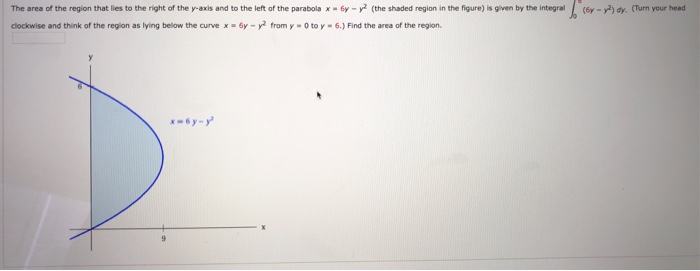
Answered Area Of The Region That Lies To The Bartleby
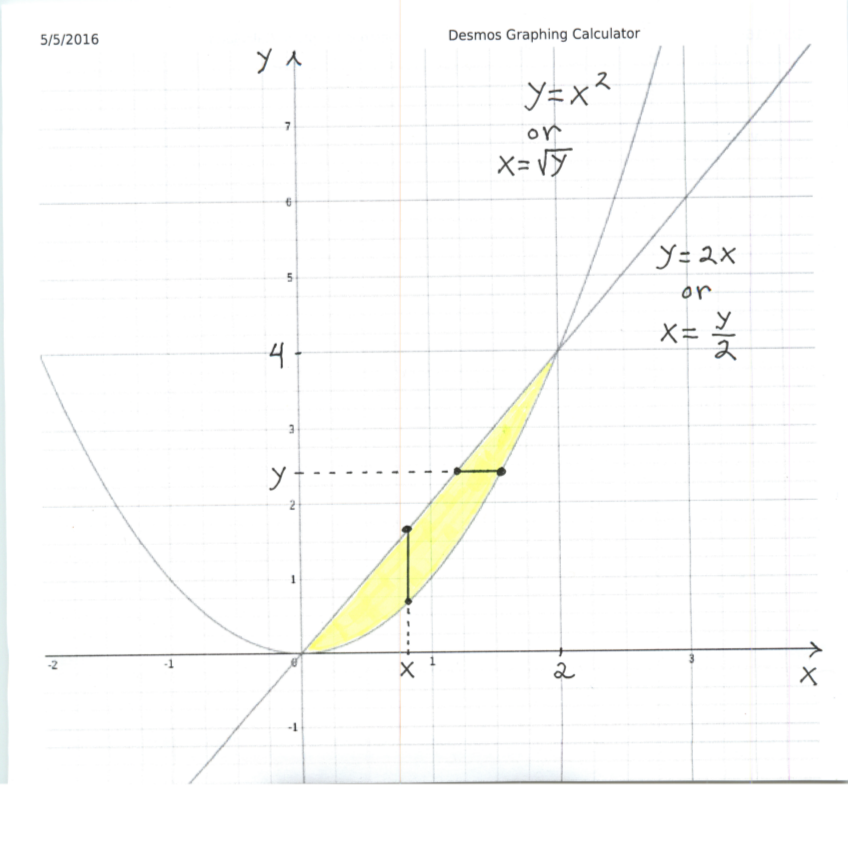
Areas Of Enclosed Regions
4a Volume Of Solid Of Revolution By Integration Disk Method

Logarithm Wikipedia

Solved The Following Figure Shows The Parabola Y X 2 And A Line Segment Overline A P Drawn From The Point A 0 1 To The Point P Left A A 2 Right On The Parabola Figure Can T Copy A Express The

Cc Using Definite Integrals To Find Area And Volume
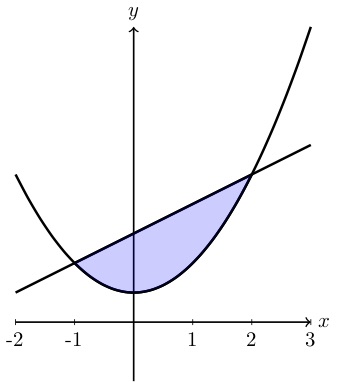
Cc Antiderivatives From Formulas

Comparison Of Grade Space Of Ifss Pfss And 3 2 Fss Download Scientific Diagram

19 Consider The Parabola Y 1 1 The Shaded Area Is Win Wi

Average Value And Area Revisited
Math Mit Edu
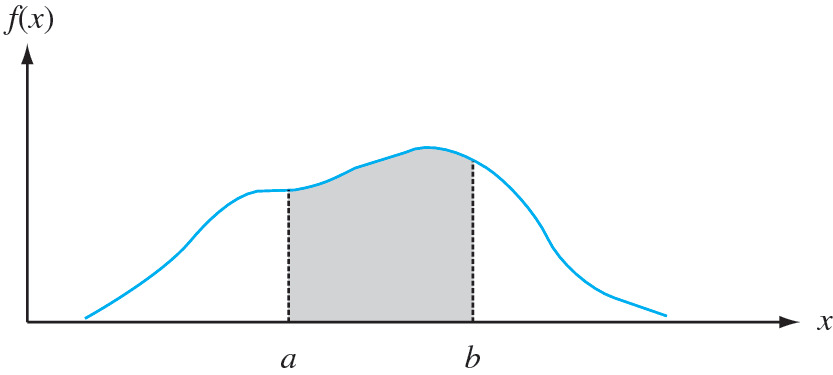
Continuous Random Variables And Probability Distributions Springerlink

19 Consider The Parabola Y X2 11 1 Solution The Shaded Area Is Win Wi 3

25 Consider The Parabola Y X2 The Shaded Area Is
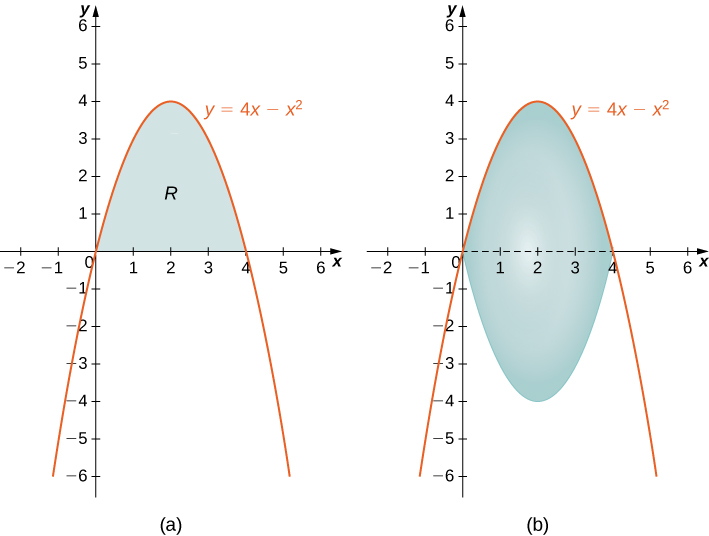
How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic
Find The Area Of The Region Enclosed By The Parabola X2 Y And The Line Y X 2 Studyrankersonline

Solved In The Figure To The Right The Equation Of The Solid Chegg Com
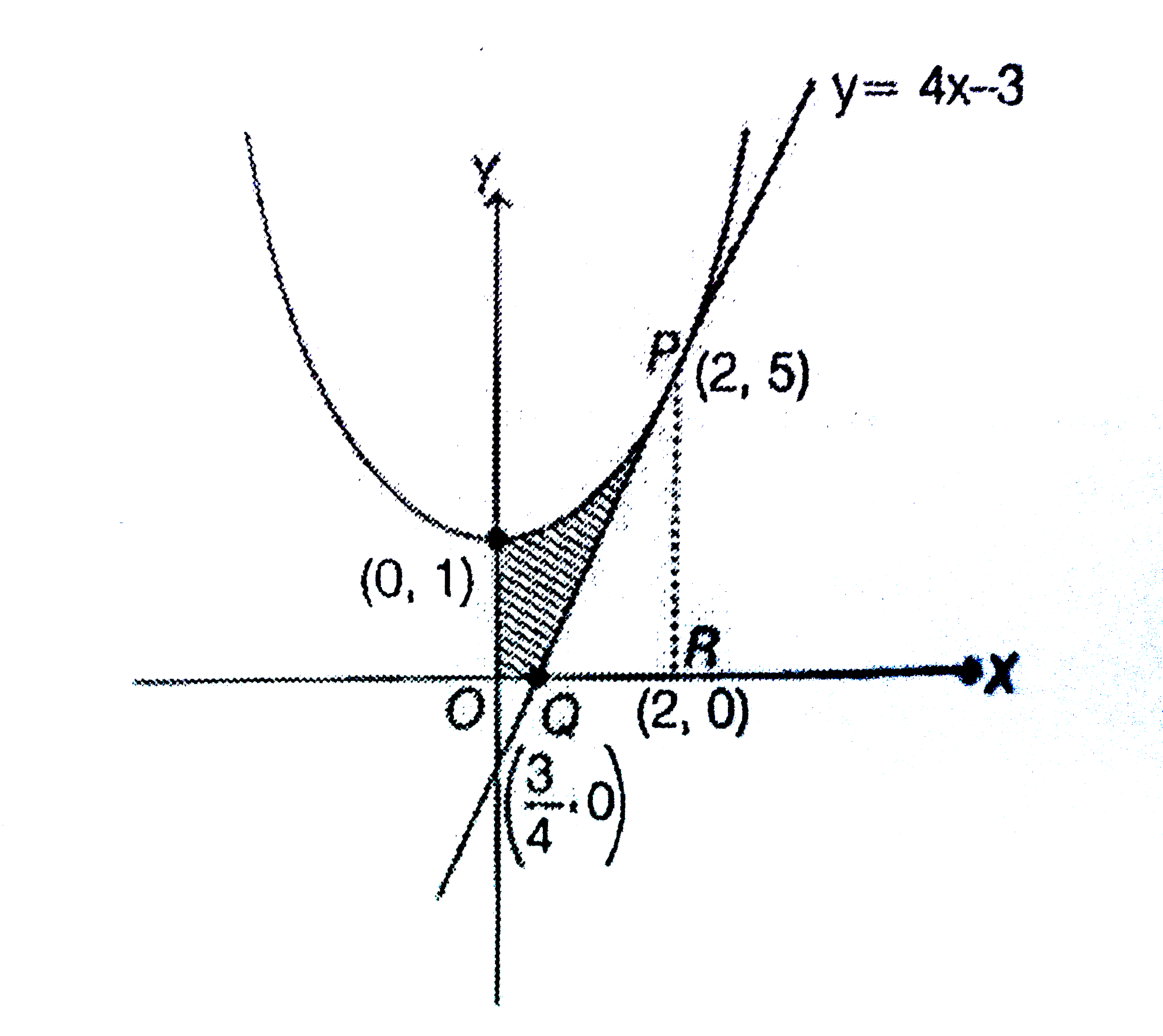
The Area In Sq Units In The First Quadrant Bounded By The Parabola Y X 2 1 The Tangent To It At The Point 2 5 And The Coordinate Axes Is
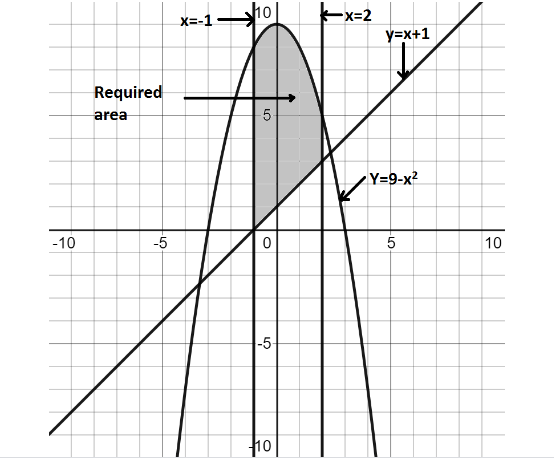
How Do You Sketch The Region Enclosed By Y X 1 Y Class 12 Maths Cbse
1

How To Fill Area Bounded By Two Parabolas In Tikz Tex Latex Stack Exchange

Let R Be The Region Bounded By The Parabola Y X 2 And The Lie Y 4 A What Is The Volume Of The Solid Generated When R Is Rotated About The Line

Determine The Centroid X Y Of The Shaded Area Youtube

Consider The Parabola Y X 2 The Shaded Area Is

Optimization Problems In 2d Geometry

Solve This 10 Consider The Parabola Y X2 The Shaded Area Is 1 232 533 734 Physics Motion In A Straight Line Meritnation Com
Sustainability Free Full Text Corporate Data Sharing Leakage And Supervision Mechanism Research Html
Area Between Two Curves Geeksforgeeks
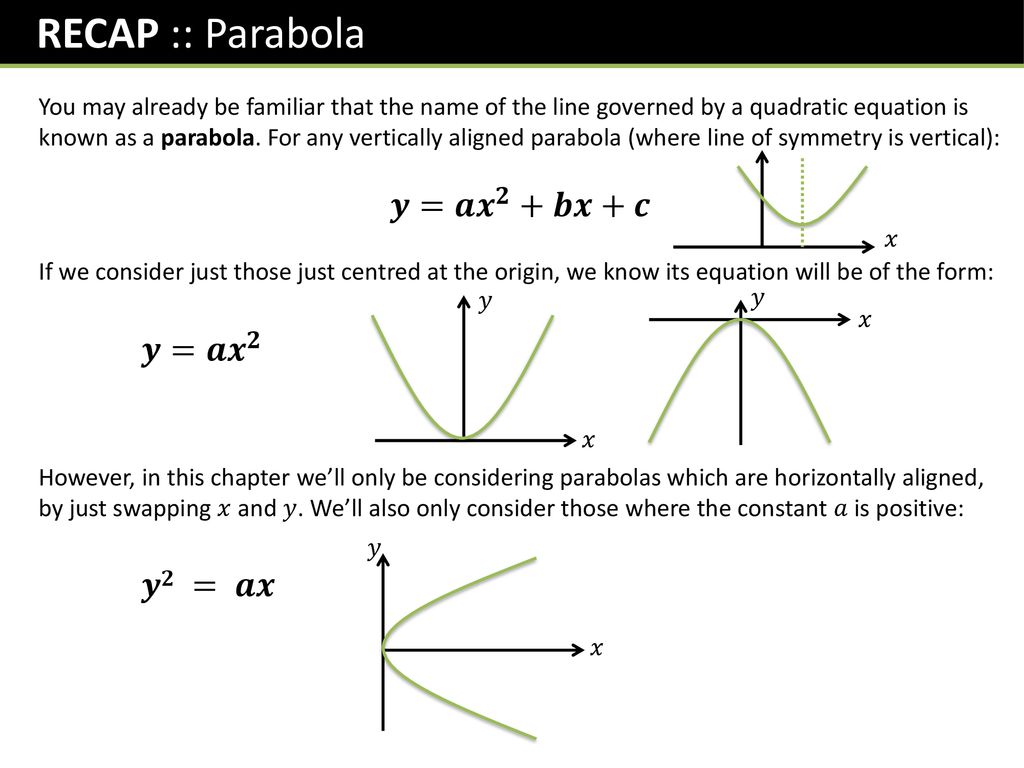
Further Pure 1 Chapter 2 Conics 1 Ppt Download
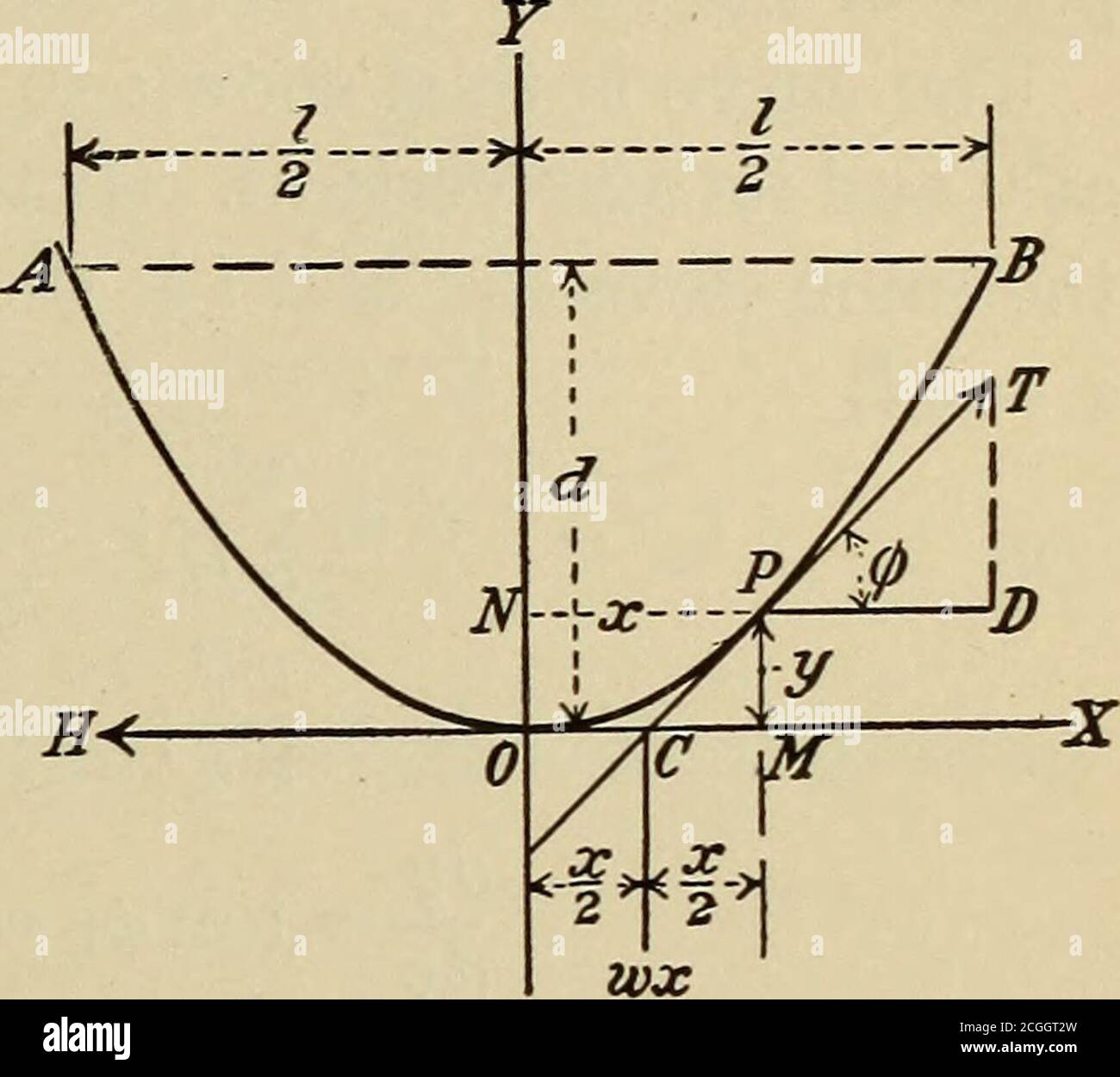
Applied Calculus Principles And Applications A J O J 0 Curve Of A Cord 241 144 Curve Of A Cord Under Uniform Horizontal Load Parabola When A Flexible Cord Supports
Mathsrevision Com
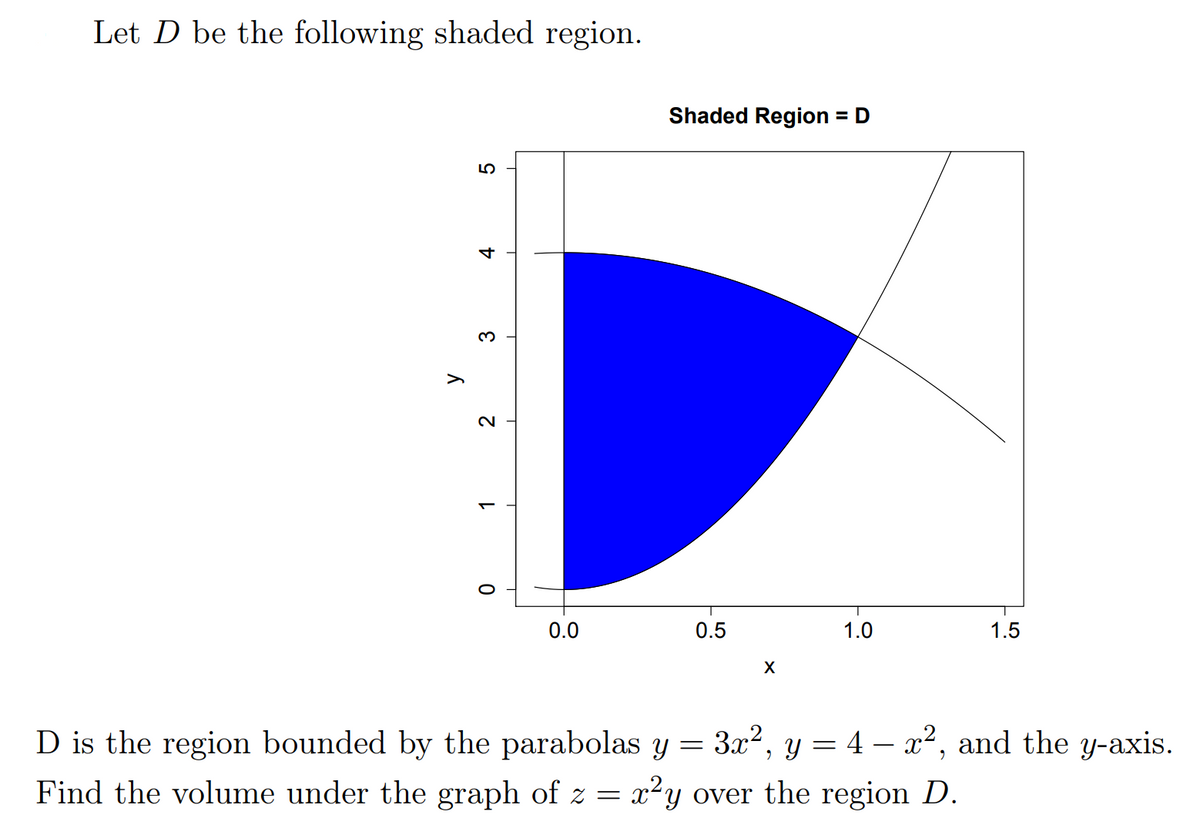
Answered Let D Be The Following Shaded Region Bartleby
Link Aps Org

In The Shaded Area The Quintics Considered Have Rank Four And Have Download Scientific Diagram
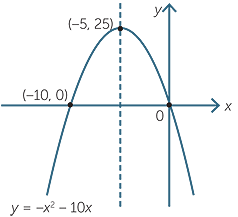
Graph The Parabola Y X 2 6x Mathskey Com

Volume Of Revolution Shell Method
Math Mit Edu
4a Volume Of Solid Of Revolution By Integration Disk Method
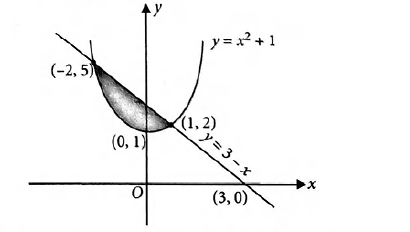
The Area Of The Region Bounded By The Parabola Y X2 1 And

Area Of A Region Bounded By Curves
Arxiv Org

Consider The Parabola Y X 2 The Shaded Area Is
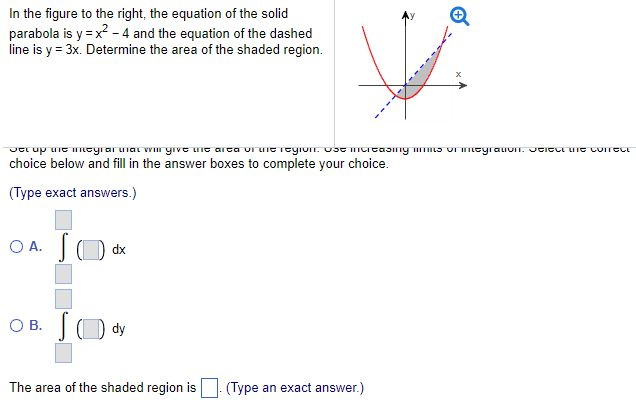
Solved In The Figure To The Right The Equation Of The Solid Chegg Com

The Shaded Area Shown Below Is Bounded By The Line X 1 M On The Left The X Axis On Top And The Curve Y 2x X 2 M On The
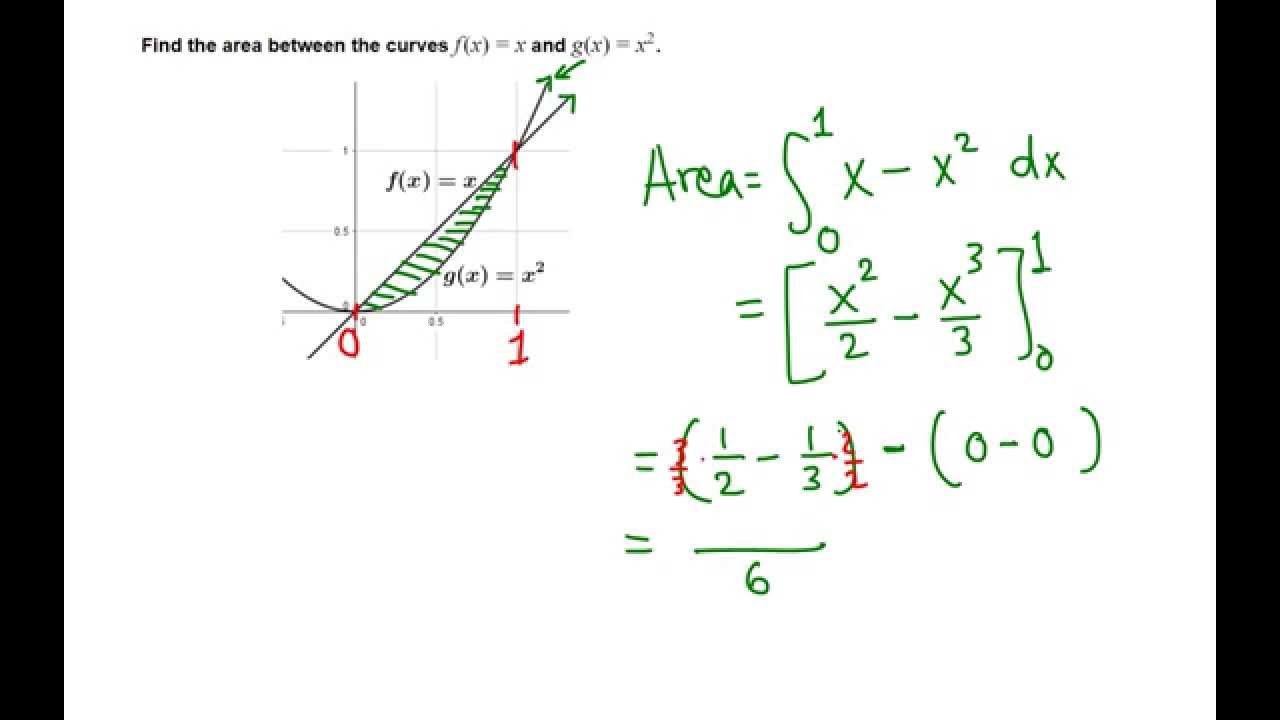
Area Between Y X And Y X 2 Youtube
How Do You Graph The Inequality Y X2 Class 11 Maths Cbse
Deepaksirmaths Weebly Com
Area Of The Region Bounded By Two Parabolas Y X2 And X Y2 Is
Louisianabelieves Com

Area Between A Curve And The 𝘺 Axis Video Khan Academy
Solution Can We Find The Area Inside A Parabola A Tangent And The X Axis Calculus Of Powers Underground Mathematics
Solution Can We Find The Area Inside A Straight Line A Parabola And The X Axis Calculus Of Powers Underground Mathematics
What Is The Area Bounded By The Curve Y X 2 And Y X Quora

5 02 Area Between Curves Lesson Mathspace

Lesson Explainer Volumes Of Solids Of Revolution Nagwa
Quadratic Function

Consider The Parabola Y X 2 The Shaded Area Is
Accessengineeringlibrary Com
Solved The Area Of The Region That Lies To The Right Of The Chegg Com

Consider The Domain D Above The X Axis And Below Parabola Y 1 X 2 In The Xy Plane A Sketch D B Express Int Int D F X Y Da As An Iterated Integral
Southhadleyschools Org

In The Given Parabola Y X2 Find The Area Of The Shaded Portion The Shaded Physics Motion In A Straight Line Meritnation Com
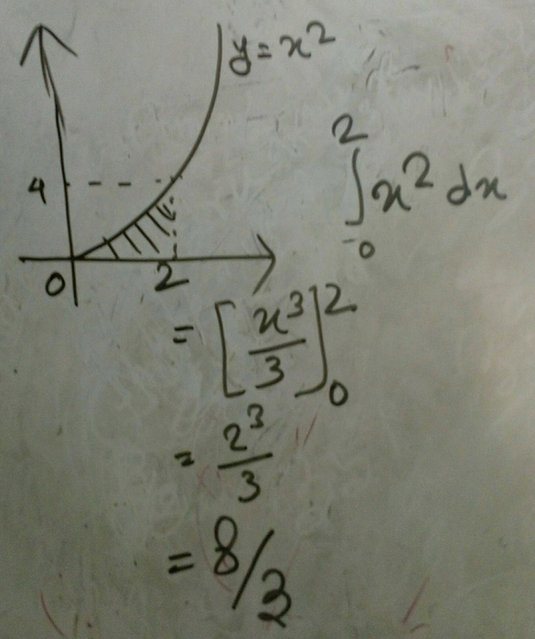
10 Consider The Parabola Yx 4 0 2 The Shaded Area Is 2 3 Scholr
Uncertain Gain And Phase Matlab Simulink
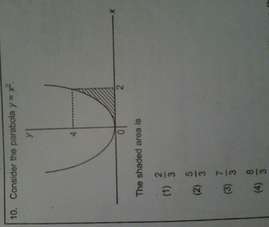
10 Consider The Parabola Yx 4 0 2 The Shaded Area Is 2 3 Scholr
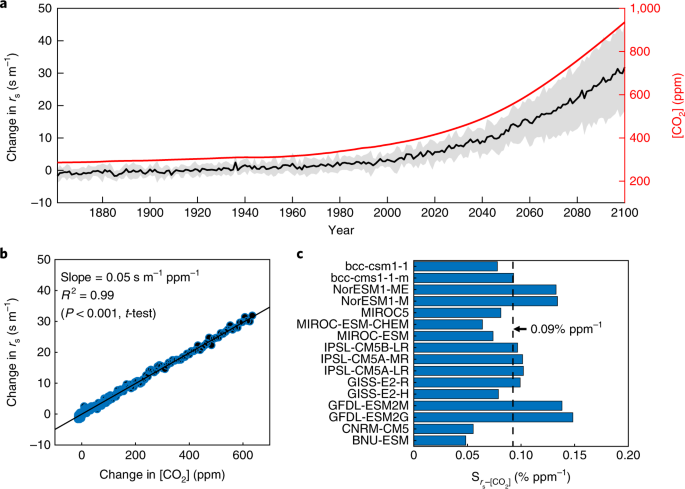
Hydrologic Implications Of Vegetation Response To Elevated Co 2 In Climate Projections Nature Climate Change
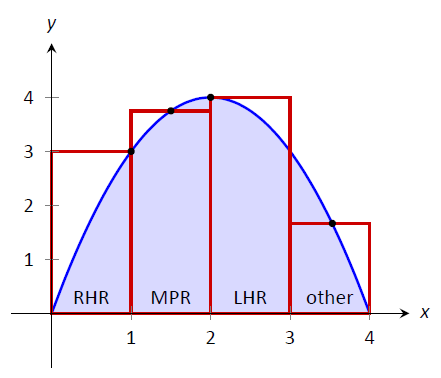
5 3 Riemann Sums Mathematics Libretexts
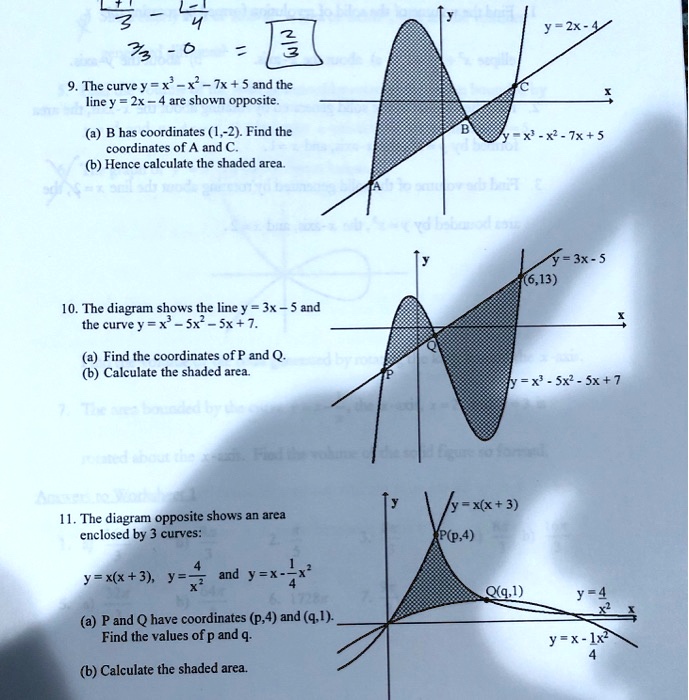
T23mynoomp7a M
Web Stevens Edu
Deepaksirmaths Weebly Com

Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
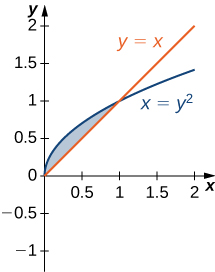
6 1 Areas Between Curves Calculus Volume 1

Ex 8 1 9 Class 12 Find Area Bounded By Parabola Y X 2 And Y X

Solved The Shaded Area Shown In Figure 1 Is Bounded By X Yaxes And The 1 Answer Transtutors
What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora

Ex 8 1 9 Class 12 Find Area Bounded By Parabola Y X 2 And Y X

Quadratic Function
6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1
What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora
Iitg Ac In
Accessengineeringlibrary Com
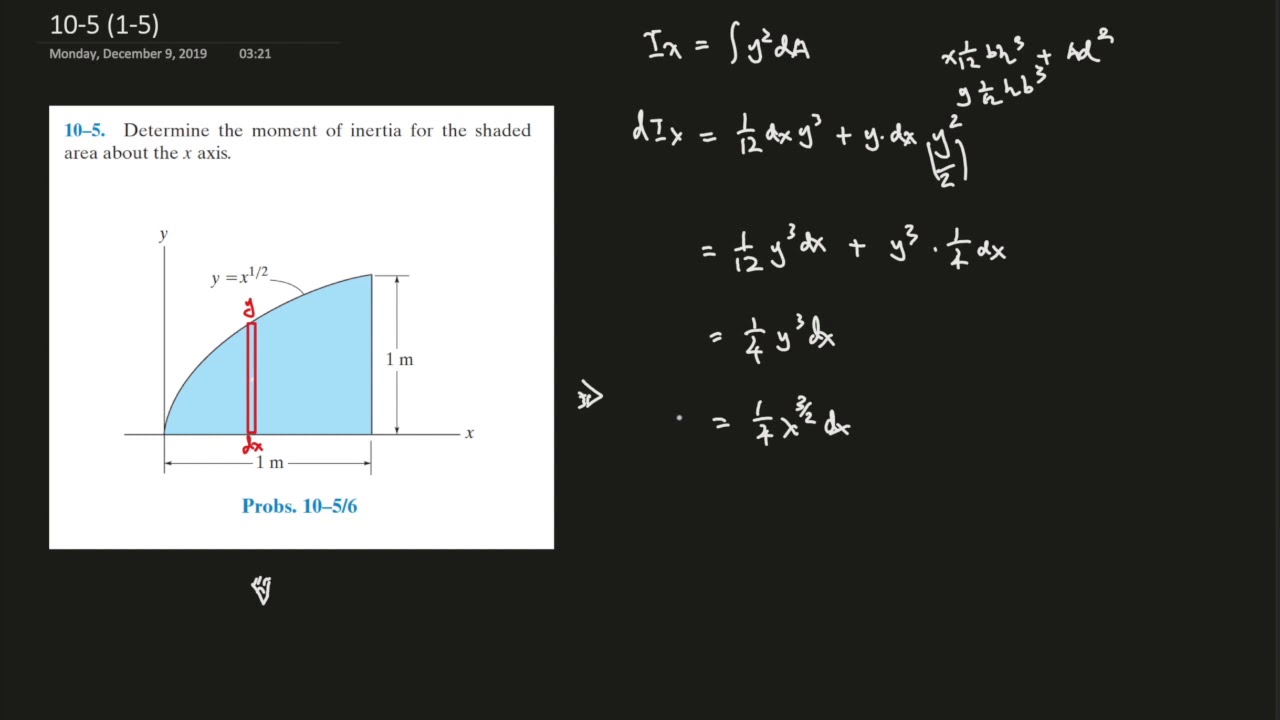
10 5 Determine The Moment Of Inertia For The Shaded Area About The X Axis Youtube
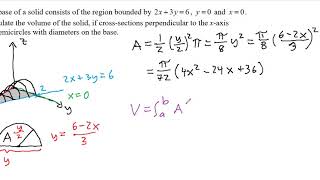
Volume Of Revolution Disk Method
Iitg Ac In
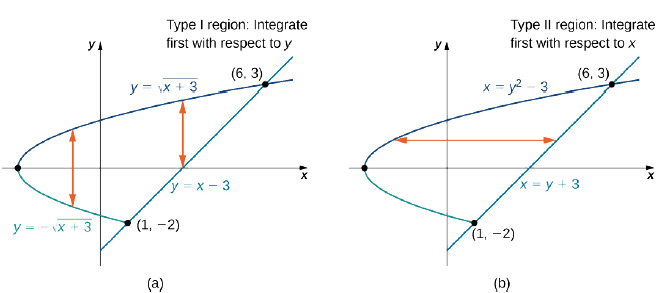
14 2 Double Integrals Over General Regions Mathematics Libretexts




